J. Cent. South Univ. (2020) 27: 3754-3767
DOI: https://doi.org/10.1007/s11771-020-4575-8
A novel line-symmetric Goldberg 6R linkage with bifurcation property
LI Lei(李磊)1, LI Teng-fei(李腾飞)1, DAI Jian-sheng(戴建生)1, 2, WANG Rui-qin(王瑞钦)1
1. Key Lab for Mechanism Theory and Equipment Design of Ministry of Education, International Centre for Advanced Mechanisms and Robotics, Tianjin University, Tianjin 300350, China;
2. Centre for Robotics Research, School of Natural Sciences and Mathematics, King’s College London, University of London, London WC2R 2LS, United Kingdom
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract:
This paper proposes a novel reconfigurable Goldberg 6R linkage, conformed to the construction of variant serial Goldberg 6R linkage, while simultaneously satisfying the line-symmetric Bricard qualifications. The isomeric mechanism of this novel reconfigurable mechanism is obtained in combination with the isomerization method. The geometrically constrained conditions result in variable motion branches of the mechanism. Based on the singular value decomposition of the Jacobian matrix, the motion branches and branch bifurcation characteristics are analyzed, and the schematics of bifurcations in joint space is derived. This novel 6R linkage features one Goldberg 6R motion branch, two line-symmetric Bricard 6R motion branches, and one Bennett motion branch. With regards to the line-symmetric Bricard 6R motion branches, a similar function for the disassembly and recombination process can be achieved by reconstructing an intermediate configuration through bifurcation. Then, the isomerized generalized variant Goldberg 6R linkage is explicated in a similar way. Acting as a bridge, reconfigurability connects two families of overconstrained mechanisms.
Key words:
overconstrained mechanism; reconfigurable mechanism; SVD method; bifurcation characteristics；
Cite this article as:
LI Lei, LI Teng-fei, DAI Jian-sheng, WANG Rui-qin. A novel line-symmetric Goldberg 6R linkage with bifurcation property [J]. Journal of Central South University, 2020, 27(12): 3754-3767.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-020-4575-81 Introduction
An overconstrained mechanism is a type of spatial mechanism which does not conform to Grübler-Kutzbach mobility criterion [1]. Due to its unit kinetic characteristic, an overconstrained mechanism has attracted numerous great scholars to explore its reason for overconstraint, kinetic analysis, dynamic analysis, and singularity over the last century and a half. Spatial 6R linkages are the most widely studied overconstrained mechanisms, which are primarily divided into two categories. One category accommodates six kinds of Bricard mechanisms [2, 3], as well as the overconstrained mechanisms derived from it. BRICARD [3] discovered six invertible forms while studying invertible hexahedron and boiled them down into six overconstrained 6R linkages. These mechanisms form the Bricard family. Bricard mechanisms are often symmetric during motion. The other category is the construction of 6R linkages with all kinds of construction methods, on the basis of Bennett mechanism [4] and Goldberg 5R linkage [5]. This kind of linkages forms the Bennett family. By connecting a Goldberg 5R linkage and a Bennett linkage in series, Goldberg built a serial Goldberg 6R linkage [6]. In 1993, by further utilization of the method of Goldberg, BAKER [7] changed the revolute pairfixed in the 6R linkage and proposed one kind of variant Goldberg 6R linkages, i.e., variant serial Goldberg 6R linkage.
Overconstrained 6R linkages do not comprise of only Goldberg 6R linkages and Bricard 6R linkages. Likewise, the construction methods of overconstrained linkages are also not limited to the method of removing common linkage, as proposed and used by GOLDBERG. For example, WALDRON [8] proposed an approach to construct a series of overconstrained mechanisms by sharing a joint axis between any two 4R linkages and removing the common joint. SONG et al [9] established an overconstrained mechanism by adding two extra joints to Bennett linkage. MAVROIDIS et al [10, 11] built Bennett-joint 6R linkage and Dietmaier 6R linkage with different numerical methods. LI et al [12] discovered a new mobile 6R linkage by deriving the equations for a bond diagram. ZHANG et al [13] presented two overconstrained 6R linkages evolved from a novel metamorphic 8R linkage.
The reconfigurable mechanisms were coined in 1990s [14], and gradually become a hot spot for researches. Currently, there are many types of reconfigurable mechanisms, including the kine- matotropic mechanisms presented by WOHLHART [15], the metamorphic mechanisms investigated by DAI et al [16], mechanisms with variable topologies proposed by YAN et al [17], and mechanisms with multiple modes introduced by WOHLLART [18]. GALLETTI et al [19] designed a series of kinematotropy mechanisms using the displacement group method. KONG et al [20] addressed a new approach to building variable-DOF 7R and 8R linkages by inserting two revolute joints of a planar mechanism. KONG et al [21-24] proposed many single-closed loop and single-DOF mechanisms with two operating modes. SONG et al [25] differed in the revised general line-symmetric Bricard linkage from the original general line- symmetric Bricard linkage. FENG et al [26] proposed the explicit solution of the general plane- symmetric Bricard linkage and the bifurcation between the general plane-symmetric Bricard linkage and the Bennett linkage. ZHANG et al [27] presented a metamorphic linkage with a trifurcation point by making one limb as Sarrus linkage concurrent. MA et al [28] proposed two novel reconfigurable linkages as the spherical-planar 6R metamorphic linkage and the Bennett-spherical 6R metamorphic linkage. KANG et al [29] presented the third- and fourth-order based method for their bifurcation revelation using screw theory. LUO et al [30] proposed a reconfigurable tracked mobile robot based on four-linkage mechanism. ZHAO et al [31] proposed a metamorphic quadruped walking robot with a changeable waist.
The linkages in Bennett-based family emphasize the construction methods. The linkages in Bricard-related family lay emphasis on the geometry conditions. Therefore, it is possible that a linkage in Bennett-based family conforms the geometry conditions of the Bricard linkages. This paper proposes a novel line-symmetric Goldberg 6R linkage which satisfies the line-symmetric Bricard qualifications. It belongs to both the overconstrained mechanism and the reconfigurable mechanism. Meanwhile, combined with the method of isomerization proposed by WOLHART [32], the isomeric mechanism of this novel reconfigurable mechanism is obtained. The changes of the motion branches through the bifurcations are elaborated and the relationship between the Bennett-based and Bricard-related families is established through the reconfiguration.
2 Line-symmetric Goldberg linkage 6r integration approach
2.1 Line-symmetric Goldberg 6R linkage
To describe a mechanism, D-H parameters [33] of the links are used as shown in Figure 1. Here, zi is the axis along the axis of revolute joint i, and xi+1 is the axis along the common normal direction from zi to zi+1. The link length ai(i+1) is the common perpendicular distance of two adjacent joint axes from zi to zi+1 positively along xi+1. The link twist angle αi(i+1) is the space angle from zi to zi+1 positively about xi+1. The offset Ri is the common normal distance of joint i from xi+ to xi+1 positively along zi. θi is the rotation angle of joint i from xi to xi+1 positively about zi.
The line-symmetric Goldberg 6R linkage is constructed from three Bennett loops. The construction methods of classic and variant serial Goldberg 6R linkages are shown in Figure 2.
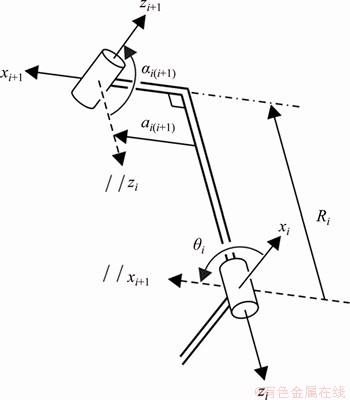
Figure 1 Link coordinate frames and parameters of classical D-H convention
Three Bennett linkages with a link b/β in common were placed in serial for combination. Different from the classic serial Goldberg 6R linkage, for variant serial Goldberg 6R linkages, one kink angle of link-pair a/α-c/γ at the bottom left and another kink angle of link-pair c/γ-d/δ at the top right were locked to zero. After removing the superposed links and joints, the variant serial Goldberg 6R linkage can be formed.
To construct the line-symmetric Goldberg 6R linkage, the same Bennett mechanisms are selected on the left and right sides as shown in Figures 3 and 4, i.e., to add the following condition to the linkage:
a/α=d/δ (1)
The geometric parameters of the 6R linkage thus constructed are line-symmetric, and the geometric parameters are as follows:
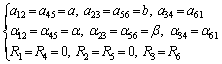(2)
For the purpose of generalisation, when two joints are locked, joints are not arranged collinearly, but locked as θk. At this moment, a34, α34 and R3 can be calculated through spatial triangle [34, 35].
From the construction form, this 6R linkage conforms to the construction form of variant serial Goldberg 6R linkage. Therefore, there is a motion branch of Goldberg 6R linkage. On the other hand, from geometric parameters, it complies with the parameters of line-symmetric Bricard mechanisms. Therefore, there is a motion branch of line-symmetric Bricard 6R linkage. Due to the symmetry of the structure, the following is also always true throughout motion branch of line- symmetric Bricard 6R linkage:
θ1=θ4, θ2=θ5, θ3=θ6 (3)
There are at least two different motion branches. So, this linkage is a reconfigurable linkage. However, the possible existence of other motion branches and the motion-branch transformation cannot be determined directly.
Figure 2 Construction of serial Goldberg 6R linkage:
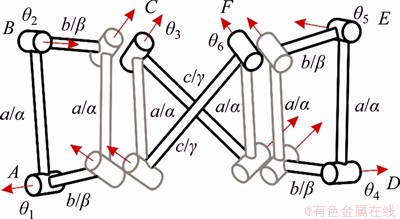
Figure 3 Construction method of novel line-symmetric Goldberg 6R linkage
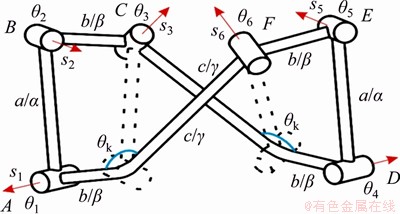
Figure 4 Novel line-symmetric Goldberg 6R linkage
2.2 Isomeric mechanism of line-symmetric Goldberg 6R linkage
WOHLHART [32] put forward the construction method of isomerization in 1991, i.e., the sharing of two adjacent bar groups of a single Bennett linkage with two adjacent bars of a movable overconstrained mechanism, and the removal of the overlapped bar groups. The resulting mechanism is called the isomeric mechanism of this linkage. This mechanism is still movable. Based on this principle, as shown in Figure 5, Bennett mechanism BAOC and line-symmetric Goldberg linkage AOCDEF share the same bar group, AOC. After this shared bar group is removed, the isomeric mechanism of the line-symmetric Goldberg 6R linkage can be derived.
Figure 5 Construction of isomeric mechanism of line-symmetric Goldberg 6R linkage
The geometric conditions of this novel linkage are as follows:
(4)
where a, b, β and R3 are the same as the parameters in Eq. (2).
3 Multiple motion branches of line- symmetric Goldberg 6R linkage
It is often difficult to analyze a reconfigurable mechanism and solve the explicit expression of its motion branches accurately due to the complexity of its closed-loop structure, the presence of many types of motion branches during motion, together with the changes in the instantaneous range of motion at bifurcation points. At present, the commonly used methods to solve the branches of motions are mainly divided into the following: the solution method of the closed-loop equation based on the classical DH method, the numerical method [36] based on the singular value decomposition (SVD) of the Jacobian matrix, the screw method to describe the geometric characteristics and constraints of the mechanism using screw, and the solution method based on dual quaternions.
The solution method based on the closed-loop equation requires solving the functional equation containing multiple unknowns, which requires a large number of calculations and sound technical skills. The screw method suffers from certain limitations. It is not easy to express the screws of some mechanism in certain configurations. The dual quaternion method is a very useful method to solve the configuration space of closed-loop linkages, which leads to polynomial functions rather than transcendental functions. However, this method needs computational methods of symbol algebra and also introduces extra variables, thus further complicating the analysis. The numerical method based on SVD can obtain the motion branches and bifurcation points of the mechanism effectively based on simple matrix theory. A singular valve detects the bifurcation points and the estimated-correction process determines the bifurcation branches. Thus, it is widely used and convenient in practical analysis. For example, it was with this method that CHEN et al [37] managed to analyze line-plane-symmetric Bricard mechanisms and CHAI et al [38] analyzed line- symmetric Waldron mechanism. Furthermore, this method is also used in the analysis of novel linkage in this paper.
For the spatial closed-loop 6R linkage, a movable mechanism has, at the very least, 1 range of motion, so its sixth singular value SV6 is always zero. Moreover, the null point of the fifth singular value SV5 means that the mechanism has two motion tendencies at this point, i.e., the bifurcation points of mechanism. Also, this numerical method can effectively obtain the motion branches and bifurcation points of the mechanism, and the complicated iteration process can be completed using a computer program. The geometric parameters of the bar lengths selected in the calculation example are:
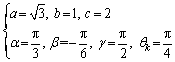(5)
The kinematics paths of the linkage are shown in Figure 6. Here, the joint angle θ2 which can rotate under many branches is selected as the input angle and θ3 is selected as the output angle. There are four kinematics paths. These four lines intersect to four bifurcation points, symbolised with the BI, BII, BIII, and BIV. All motion branches and the branch switch of this line-symmetric Goldberg 6R linkage are as follows.
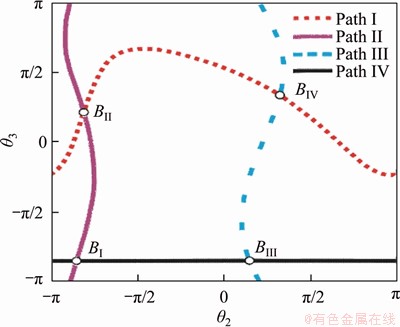
Figure 6 Kinematics paths of linkage
3.1 Motion branch 1: original Goldberg 6R linkage
Motion branch 1 is the motion branch of the linkage when the construction of the line-symmetric Goldberg 6R linkage was complete. The configuration of motion branch 1 is shown in Figure 7. Using the numerical method of SVD, the kinematic paths of the motion branch are obtained, as shown in Figure 8. In the process of motion, all of the six joints can rotate, from which it is evident that there are no two joints with consistent angles all the time, i.e., this motion branch of linkage is not symmetrical. It is the original Goldberg 6R motion branch.
Figure 7 Configuration of original Goldberg 6R linkage
The SVD results of the Goldberg 6R motion branch are shown in Figure 9. Its sixth singular value SV6 is always zero, which suggests that there is at least one such motion branch in the whole motion cycle.
At points BII and BIV, the fifth singular value SV5 falls to zero, which means that there are two instantaneous ranges of motion at these two points, and they can bifurcate to other motion branches.
The bifurcation condition at point BII is that a part of bar CD and bar FA are coaxial, and joint 3 and joint 6 are concentrated. The configuration is shown in Figure 10. The bifurcation condition at point BIV is that a part of bar CD and bar FA are coaxial, and joint 3 and joint 6 are decentralized. The configuration is shown in Figure 11.
3.2 Motion branch 2: line-symmetric Bricard 6R linkage
The linkage at point BII can be switched from variant serial Goldberg 6R motion branch to the first line-symmetric Bricard 6R motion branch. The configuration of motion branch 2 is shown in Figure 12.
Under motion branch 2, the relation curve between various joint variables and the input angle θ2 and the relation curve between the singular value and the input angle θ2 are shown in Figures 13 and 14, respectively. From the kinematic paths in Figure 13, it can be seen that the following is always true throughout the kinematic cycle of the linkage:
θ1=θ4, θ2=θ5, θ3=θ6 (6)
It can be inferred from here that this is a line-symmetric Bricard 6R motion branch. In addition, in the singular value curve of this linkage, the fifth singular value SV5 falls to zero at points BI and BII, which means that motion branch 2 can also bifurcate and switch to another two motion branches at these two points, and switch to motion branch 1 at point BII.
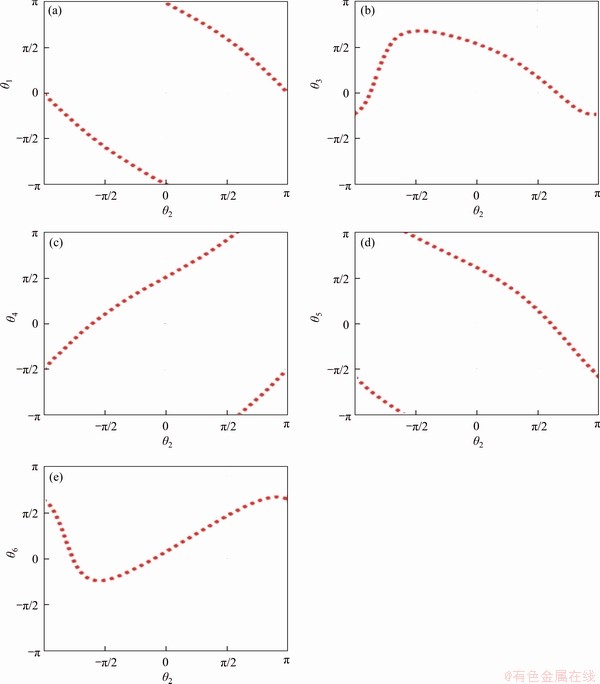
Figure 8 Kinematic paths of Goldberg 6R motion branch
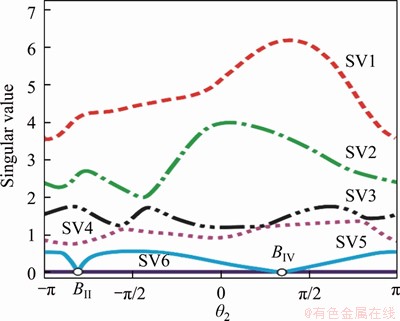
Figure 9 SVD results of Goldberg 6R motion branch
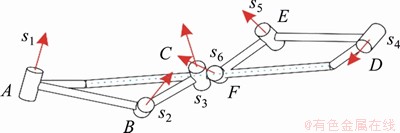
Figure 10 Configuration of linkage at bifurcation II
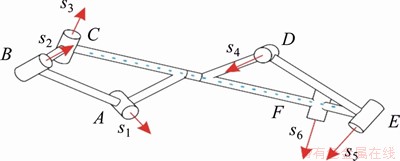
Figure 11 Configuration of linkage at bifurcation IV
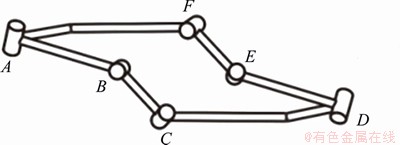
Figure 12 Configuration of line-symmetric Bricard 6R motion branch
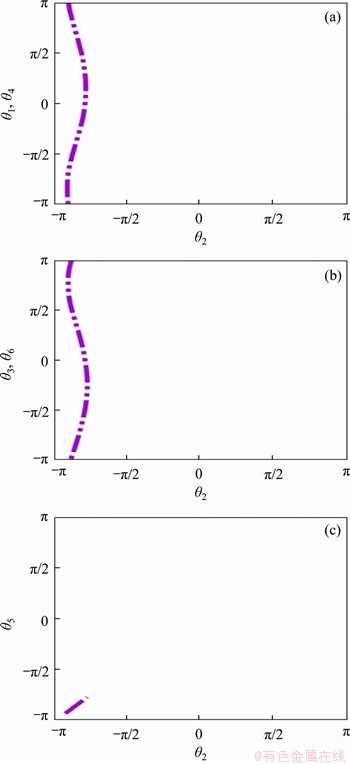
Figure 13 Kinematic paths of line-symmetric Bricard 6R motion branch
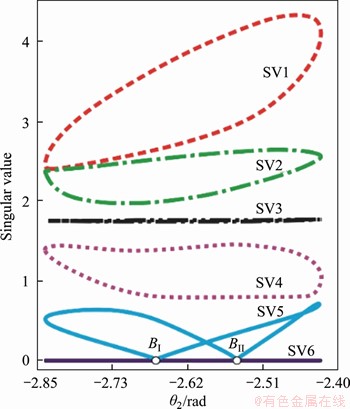
Figure 14 SVD results of line-symmetric Bricard 6R motion branch
The bifurcation condition at point BI suggests that bar AB and bar DE are coaxial and joints 2 and 5 are located between joints 1 and 4. The configuration is shown in Figure 15. Following the study of another motion branch switching from motion branch 1, the motion branch that indicates motion branch 2 and switches to at point BI will be examined.
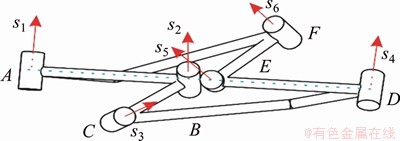
Figure 15 Configuration of linkage at bifurcation I
3.3 Motion branch 3: second line-symmetric Bricard 6R linkage
Similar to motion branch 2, the motion branch that motion branch 1 switches to at point BIV is examined. The configuration is shown in Figure 16. Its bars are also line-symmetric in space. Under motion branch 3, the relation curve between various joint variables and the input angle θ2 and the relation curve between the singular value and the input angle θ2 are shown in Figures 17 and 18,respectively. It can be seen from the kinematic paths that the following is also always true throughout the kinematic cycle of the linkage:
θ1=θ4, θ2=θ5, θ3=θ6 (7)
Therefore, this is also a line-symmetric motion branch, which is called the second line-symmetric Bricard 6R linkage.
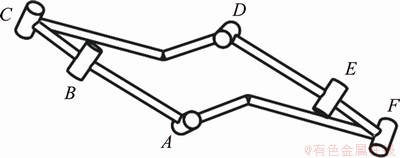
Figure 16 Configuration of second line-symmetric Bricard 6R motion branch
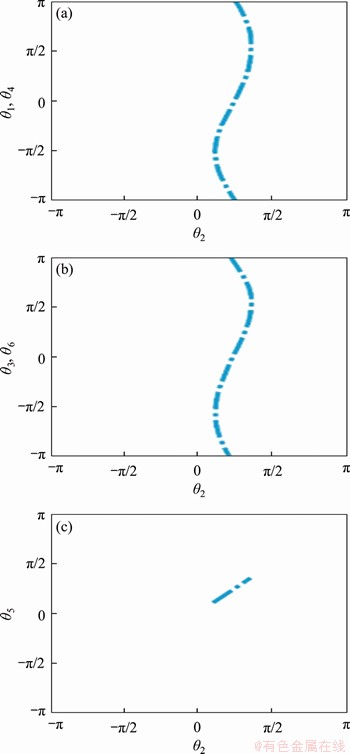
Figure 17 Kinematic paths of second line-symmetric Bricard 6R motion branch
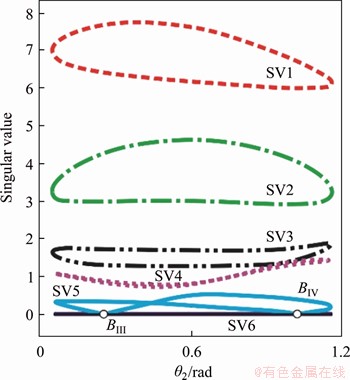
Figure 18 SVD results of second Line-symmetric Bricard 6R motion branch
While studying line-symmetric Bricard 6R linkage, SONG et al [39] discovered that for 6R linkage with the same geometric parameters, if their assembly methods are different, there will be two forms of line-symmetric Bricard 6R linkages: forward and reverse. However, both these linkages can only be switched by recombination after disassembly. Here is the result that motion branch 2 and motion branch 3 are exactly motion branches corresponding to the forward and reverse forms of line-symmetric Bricard 6R linkages with the same parameter conditions. In addition, they can’t be bifurcated to each other directly. The difference is that there is no need to disassemble and recombine. Instead, a similar function for disassembly and recombination can be achieved by reconstructing an intermediate configuration through bifurcation, i.e., motion branch 1.
In the singular value curve of the linkage shown in Figure 15, the fifth singular value SV5 falls to zero at points BIII and BIV, which means that motion branch 3 can also bifurcate and switch to another two motion branches at these two points, and switch to motion branch 1 at point BIV.
The bifurcation condition at point BIII is that bar AB and bar DE are coaxial, and joints 1 and 4 are located between joints 2 and 5. The configuration is shown in Figure 19.
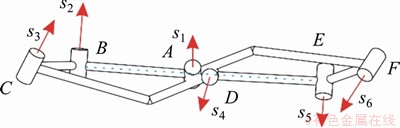
Figure 19 Configuration of linkage at bifurcation III
3.4 Motion branch 4: Bennett mechanism
When motion branch 2 is located at point BI, the linkage can be switched to the Bennett motion branch. At the bifurcation point, joints 1, 2, 5 and 4 are collinear, while joints 2 and 5 are located between joints 1 and 4. When motion branch 3 is located at point BIII, the linkage can be switched to Bennett motion branch also. At the bifurcation point, joints 1, 2, 5 and 4 are collinear, and joints 1 and 4 are located between joints 2 and 5. The configuration of motion branch 4 in the process of motion is shown in Figure 20.
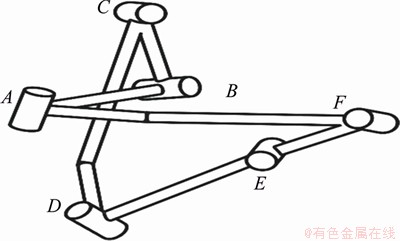
Figure 20 Configuration of Bennett 4R motion branch
Under motion branch 4, the relation curve between various joint variables and the input angle θ2, and the relation curve between the singular value and the input angle are shown in Figures 21 and 22, respectively. From the kinematic paths in Figure 21, it can be seen that the following is always true throughout the kinematic cycle of the linkage:
θ3=θ6=Const (8)
Joints 3 and 6 remain still and only four joints can rotate. Since there is only one type of overconstrained 4R linkage, it can be inferred that this is a Bennett motion branch.
Figure 21 Kinematic paths of Bennett 4R motion branch
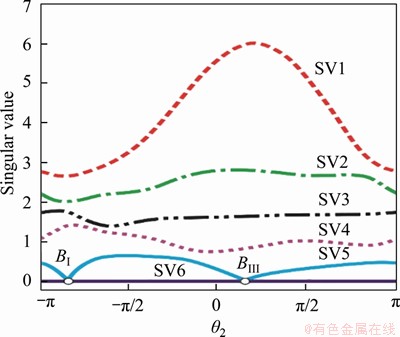
Figure 22 SVD results of Bennett 4R motion branch
Furthermore, in the singular value curve of the linkage, the sixth singular value SV6 is always zero, indicating that there is at least one range of motion in the whole cycle of motion branch 4. The fifth singular value SV5 falls to zero at points BI and BIII, which precisely corresponds to the fact that motion branch 4 switches to motion branch 2 at point BI and switches to motion branch 3 at point BIII.
3.5 Bifurcations in joint space
Through the above research, the relationship among all motion branches of this line-symmetric Goldberg 6R linkage in joint space is obtained, as shown in Figure 23. θ2 is selected as the input angle and θ3 is selected as the output angle.
The red dotted line in the figure stands for Goldberg 6R motion branch, whose complete motion cycle can be represented as a-b-d-c. The purple double-dot dash line stands for the first line-symmetric Bricard 6R motion branch, whose complete motion cycle can be represented as l-n-m-o-p. The blue dot dash line stands for the second line-symmetric Bricard 6R motion branch, whose complete motion cycle can be represented as e-d-f-g-h. The black solid line stands for Bennett motion branch, whose complete motion cycle can be represented as i-h-j-k-l. These four curves intersect and form a total of four bifurcation points. The configuration l is the bifurcation configuration of the first line-symmetric Bricard 6R motion branch and Bennett motion branch. The configuration m is the bifurcation configuration of the first line-symmetric Bricard 6R motion branch and Goldberg 6R motion branch. The configuration h is the bifurcation configuration of the second line-symmetric Bricard 6R motion branch and Bennett motion branch. The configuration d is the bifurcation configuration of the second line- symmetric Bricard 6R motion branch and Goldberg 6R motion branch. Combined with the singular value curve, the bifurcation configurations l, m, h and d correspond to the bifurcation points BI, BII, BIII and BIV, respectively.
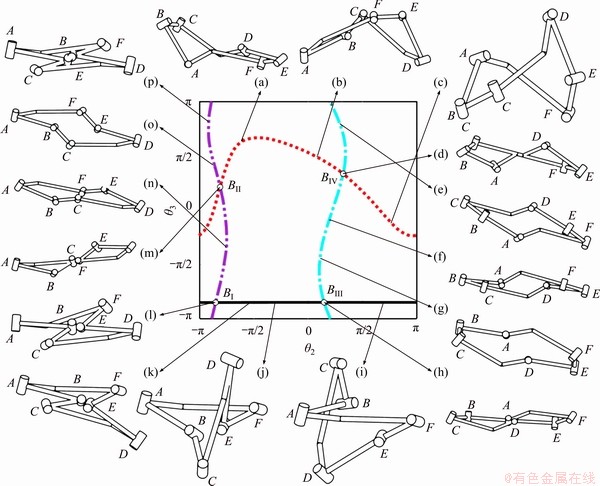
Figure 23 Bifurcations of line-symmetric Goldberg 6R linkage
Considered together, this line-symmetric Goldberg 6R linkage features 1 Goldberg 6R motion branch, 2 line-symmetric Bricard 6R motion branches and 1 Bennett motion branch. Among them, 2 line-symmetric Bricard 6R motion branches can not be switched to each other, but both of them can be switched to Goldberg 6R and Bennett 4R motion branches. Similarly, Goldberg 6R and Bennett 4R motion branches cannot be switched to each other directly. However, both of them can be switched to two line-symmetric Bricard 6R motion branches. That is to say, the linkages of the Bennett family and the linkages of the Bricard family cannot be switched within the family directly but they can be switched through a linkage of an alien family. Through reconfigurability, the relationship between the Bennett-based and Bricard-related families is established.
4 Multiple motion branches of isomeric mechanism of line-symmetric Goldberg 6R linkage
For the isomeric mechanism, the same parameters of bar length as in the previous section are selected.
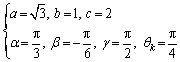(9)
Joint 6 is set as the input angle and joint 3 is set as the output angle. The relation curve between the input angle and output angles is obtained as shown in Figure 24. It is discovered that there are also four motion branches, which intersect and form four bifurcation points. After research, their forms of motion correspond to the original linkage separately. The analysis process is similar to the above and the conclusion is given without further elaboration.
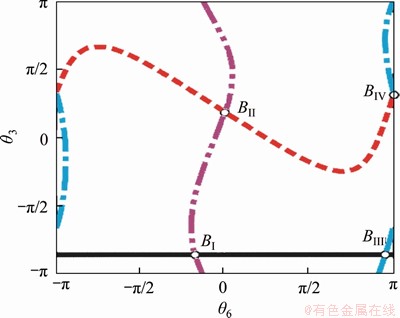
Figure 24 Kinematic paths of isomeric line-symmetric Goldberg 6R linkage
The relationship among all motion branches of the isomeric line-symmetric Goldberg 6R linkage in joint space is shown in Figure 25.
The red dotted line in the figure stands for the degenerated Goldberg 5R motion branch, whose complete motion cycle can be represented as a-b-m-c-d. The purple double-dot dash line stands for the first isomeric line-symmetric 6R motion branch, whose complete motion cycle can be represented as l-n-o-m-p. The blue dot dash line stands for the second isomeric line-symmetric 6R motion branch, whose complete motion cycle can be represented as e-d-f-g-h, and the black solid line stands for the generalised Goldberg 5R motion branch, whose complete motion cycle can be represented as h-i-j-l-k. These four motion branches intersect at four bifurcation points. The configuration l is the bifurcation configuration of the generalised Goldberg 5R motion branch and the first isomeric line-symmetric 6R motion branch. The configuration m is the bifurcation configuration of the degenerated Goldberg 5R motion branch and the first isomeric line-symmetric 6R motion branch. The configuration h is the bifurcation configuration of the generalised Goldberg 5R motion branch and the second isomeric line-symmetric 6R motion branch. The configuration d is the bifurcation configuration of the degenerated Goldberg 5R motion branch and the second isomeric line- symmetric 6R motion branch. Combined with the singular value curve, the bifurcation configurations l, m, h and d correspond to the bifurcation points BI, BII, BIII and BIV, respectively.
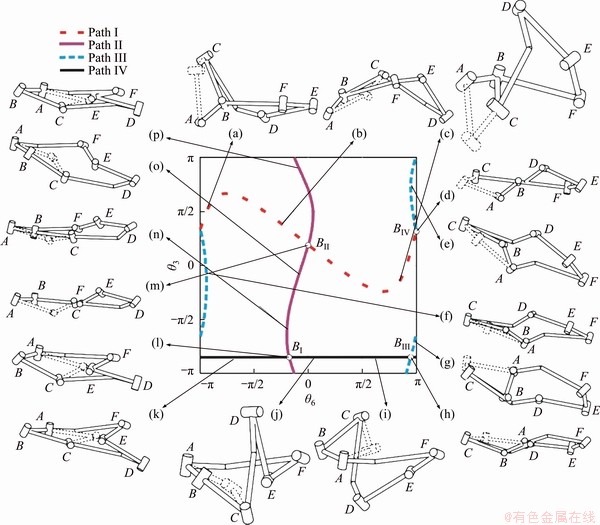
Figure 25 Bifurcations of isomeric line-symmetric Goldberg 6R linkage
This isomeric line-symmetric Goldberg 6R linkage features 1 degenerated Goldberg 5R motion branch, 2 isomeric line-symmetric 6R motion branches, and 1 generalized Goldberg 5R motion branch. Similar to the linkage before isomerization, four motion branches form four bifurcation points. The linkages of the Bennett family and the linkages of the Bricard family cannot be switched within the family directly, but they can be switched through a linkage of an alien family. For the mechanism proposed in this paper, isomerization wouldn’t change the switch relationship between the motion branches bifurcated, the number of bifurcation points or even the configuration characteristics at bifurcation points. The only other deviation is simply the specific form of motion branches. For example, the number of movable bars may change and the intrinsic line-symmetric form of the linkage may change its representation form.
5 Conclusions
A novel line-symmetric Goldberg 6R linkage was constructed in this paper through the addition of line-symmetric condition to the linkage. Then, its bifurcation characteristics were analyzed in detail, which mainly include the identification of motion branches as well as the bifurcation and switch relationship among these motion branches. Through two bifurcations and switches, a similar effect to disassembly and reverse assembly of the line-symmetric Bricard mechanism can be achieved. Through reconfigurability, both the Bennett family and Bricard family were bridged. Meanwhile, the bifurcation characteristics of its isomeric mechanism were also studied. These studies also open up a new passage for the construction of novel reconfigurable mechanisms. Furthermore, it is possible to discover more Goldberg linkages containing Bricard motion branches by using similar construction method.
Contributors
The overarching research goals were developed by LI Lei, LI Teng-fei, and DAI Jian-sheng. LI Lei and LI Teng-fei proposed the construction method of the new mechanism. LI Lei, LI Teng-fei and WANG Rui-qing analyzed the bifurcation characteristics of the new mechanism. The schematic of bifurcations in joint space is derived by LI Lei. The initial draft of the manuscript was written by LI Lei, LI Teng-fei, and WANG Rui-qin. All authors replied to reviewers’ comments and revised the final version.
Conflict of interest
LI Lei, LI Teng-fei, DAI Jian-sheng and WANG Rui-qin declare that they have no conflict of interest.
References
[1] DAI J S, HUANG Zhen, LIPKIN H. Mobility of overconstrained parallel mechanisms [J]. Journal of Mechanical Design, 2006, 128(1): 220-229. DOI: 10.1115/ 1.1901708.
[2] BRICARD R. Treatise on the theory of articulated octabedrouns [J]. Journal de Mathématiques Pures et Appliquées, 1897, 3: 113-148. https://eudml.org/doc/234618. (in French)
[3] BRICARD R. Dynamics course [M]. Paris: Gauthier-Villars, 1926. DOI: 10.1007/BF01696329. (in French)
[4] BENNETT G T. A new mechanism [J]. Engineering, 1903, 76: 777. https://ci.nii.ac.jp/naid/10008651173/#cit.
[5] GOLDBERG M. New five-bar and six-bar linkages in three dimensions [J]. Transactions of ASME, 1943, 65: 649-661. https://www.researchgate.net/publication/243779884.
[6] BAKER J E. The Bennett, Goldberg and Myard linkages—in perspective [J]. Mechanism and Machine Theory, 1979, 14(4): 239-253. DOI: 10.1016/0094-114X(79)90011-9.
[7] BAKER J E. A comparative survey of the Bennett-based, 6-revolute kinematic loops [J]. Mechanism and Machine Theory, 1993, 28(1): 83-96. DOI: 10.1016/0094-114X(93) 90049-2.
[8] WALDRON K J. Hybrid overconstrained linkages [J]. Journal of Mechanisms, 1968, 3(2): 73-78. DOI: 10.1016/ 0022-2569(68)90016-5.
[9] SONG Ya-qing, MA Xue-si, DAI J S. A novel 6R metamorphic mechanism with eight motion branches and multiple furcation points [J]. Mechanism and Machine Theory, 2019, 142: 103598. DOI: 10.1016/j.mechmachtheory. 2019.103598.
[10] MAVROIDIS C, ROTH B. New and revised overconstrained mechanisms [J]. Journal of Mechanical Design, 1995, 117(1): 75-82. DOI: 10.1115/1.2826120.
[11] LI Zi-jia, SCHICHO J. A technique for deriving equational conditions on the Denavit-Hartenberg parameters of 6R linkages that are necessary for movability [J]. Mechanism and Machine Theory, 2015, 94: 1-8. DOI: 10.1016/ j.mechmachtheory.2015.07.010.
[12] ZHANG Ke-tao, DAI J S. A kirigami-inspired 8R linkage and its evolved overconstrained 6R linkages with the rotational symmetry of order two [J]. Journal of Mechanisms and Robotics, 2014, 6(2): 021007. DOI:10.1115/1.4026337. DOI: 10.1115/1.4026337.
[13] DIETMAIER P. A new 6R space mechanism [C]// Proceeding of the 9th World Congress IFToMM. Milano: Greenough J D, 1995: 52-56. https://www.researchgate. net/publication/303253349.
[14] KUO C H, DAI J S, YAN H S. Reconfiguration principles and strategies for reconfigurable mechanisms [C]// Reconfigurable Mechanisms and Robots, 2009. ReMAR 2009. ASME/IFToMM International Conference on. IEEE, 2009. https://www.researchgate.net/publication/224567486.
[15] WOHLHART K. Kinematotropic linkages [M]// Recent Advances in Robot Kinematics. Dordrecht: Springer Netherlands, 1996: 359-368. DOI: 10.1007/978-94-009- 1718-7_36.
[16] DAI J S, REES JONES J. Mobility in metamorphic mechanisms of foldable/erectable kinds [J]. Journal of Mechanical Design, 1999, 121(3): 375-382. DOI: 10.1115/1.2829470.
[17] YAN Hong-sen, KUO C H. Topological representations and characteristics of variable kinematic joints [J]. Journal of Mechanical Design, 2006, 128(2): 384-391. DOI: 10.1115/1.2166854.
[18] WOHLHART K. Multifunctional 7R linkages [C]// Proceedings of the International Symposium of Mechanism and Machine Science. Izmir, 2010 : 85-91. https://www. researchgate.net/publication/285751548.
[19] GALLETTI C, FANGHELLA P. Single-loop kinematotropic mechanisms [J]. Mechanism and Machine Theory, 2001, 36(6): 743-761. DOI: 10.1016/S0094-114X(01)00002-7.
[20] KONG Xian-wen, PFURNER M. Type synthesis and reconfiguration analysis of a class of variable-DOF single-loop mechanisms [J]. Mechanism and Machine Theory, 2015, 85: 116-128. DOI: 10.1016/j.mechmachtheory. 2014.10.011.
[21] KONG X W, HUANG C. Type synthesis of single-DOF single-loop mechanisms with two operation modes [C]// Reconfigurable Mechanisms and Robots, 2009. ReMAR 2009. ASME/IFToMM International Conference on. IEEE, 2009: 136-141. https://www.researchgate.net/publication/ 251891213.
[22] KONG Xian-wen. A variable-DOF single-loop 7R spatial mechanism with five motion modes [J]. Mechanism and Machine Theory, 2018, 120: 239-249. DOI: 10.1016/ j.mechmachtheory.2017.10.005.
[23] KONG Xian-wen. Reconfiguration analysis of multimode single-loop spatial mechanisms using dual quaternions [J]. Journal of Mechanisms and Robotics, 2017, 9(5): 051002. DOI: 10.1115/1.4037111. DOI: 10.1115/1.4037111.
[24] KONG X W. Reconfiguration analysis of a variable degrees- of-freedom parallel manipulator with both 3-DOF planar and 4-DOF 3T1R operation modes [C]// Proceedings of ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. August 21-24, 2016, Charlotte, North Carolina, USA. 2016 DOI: 10.1115/DETC201659203.
[25] SONG Chao-yang, CHEN Yan, CHEN I M. Kinematic study of the original and revised general line-symmetric bricard 6R linkages [J]. Journal of Mechanisms and Robotics, 2014, 6(3): 031002. DOI:10.1115/1.4026339.
[26] FENG Hui-juan, CHEN Y, DAI J S. Kinematic study of the general plane-symmetric Bricard linkage and its bifurcation variations [J]. Mechanism and Machine Theory, 2017, 116: 89-104. DOI: 10.1016/j.mechmachtheory.2017.05.019.
[27] ZHANG Ke-tao, DAI J S. Trifurcation of the evolved sarrus- motion linkage based on parametric constraints [M]// Advances in Robot Kinematics. Cham: Springer International Publishing, 2014: 345-353. DOI: 10.1007/978- 3-319-06698-1_36.
[28] MA Xue-si, ZHANG Ke-tao, DAI J S. Novel spherical- planar and Bennett-spherical 6R metamorphic linkages with reconfigurable motion branches [J]. Mechanism and Machine Theory, 2018, 128: 628-647. DOI: 10.1016/ j.mechmachtheory.2018.05.001.
[29] KANG X, FENG Hui-juan, DAI J S, YU Hao-yong. High-order based revelation of bifurcation of novel Schatz-inspired metamorphic mechanisms using screw theory [J]. Mechanism and Machine Theory, 2020, 152: 103931. DOI: 10.1016/j.mechmachtheory.2020.10-3931.
[30] LUO Zi-rong, SHANG Jian-zhong, ZHANG Zhi-xiong. A reconfigurable tracked mobile robot based on four-linkage mechanism [J]. Journal of Central South University, 2013, 20(1): 62-70. DOI: 10.1007/s11771-013-1460-8.
[31] ZHAO Xin, KANG Xi, DAI Jian-sheng. Gait planning and motion characteristic analysis of a metamorphic quadruped walking robot [J]. Journal of Central South University (Science and Technology), 2018, 49(9): 2168-2177. DOI: US7598695 B2. (in Chinese)
[32] WOHLHART K. On isomeric over-constrained space mechanisms [C]// Proc 8th Wld Congr. IFToMM, Prague, 1991, 1: 153-158. https://www.researchgate.net/publication/ 284670945.
[33] DENAVIT J, HARTENBERG R S. A kinematic notation for lower-pair mechanisms based on matrices [J]. ASME Journal of Applied Mechanics, 1995, 22: 215-221. https://www. researchgate.net/publication/230872768.
[34] YANG A T, FREUDENSTEIN F. Application of dual- number quaternion algebra to the analysis of spatial mechanisms [J]. Journal of Applied Mechanics, 1964, 31(2): 300-308. DOI: 10.1115/1.3629601.
[35] ROTH B. On the screw axes and other special lines associated with spatial displacements of a rigid body [J]. Journal of Engineering for Industry, 1967, 89(1): 102-110. DOI: 10.1115/1.3609977.
[36] GAN W W, PELLEGRINO S. Numerical approach to the kinematic analysis of deployable structures forming a closed loop [J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2006, 220(7): 1045-1056. DOI: 10.1243/09544 062JMES245.
[37] CHEN Y, CHAI W H. Bifurcation of a special line and plane symmetric Bricard linkage [J]. Mechanism and Machine Theory, 2011, 46(4): 515-533. DOI: 10.1016/ j.mechmachtheory.2010.11.015.
[38] CHAI Xu-heng, DAI J S. Three novel symmetric waldron– bricard metamorphic and reconfigurable mechanisms and their isomerization [J]. Journal of Mechanisms and Robotics, 2019, 11(5): 051011. DOI:10.1115/1.4044004.
[39] SONG Chao-yang, CHEN Yan, CHEN I M. Kinematic study of the original and revised general line-symmetric bricard 6R linkages [J]. Journal of Mechanisms and Robotics, 2014, 6(3): 031002. DOI:10.1115/1.4026339.
(Edited by YANG Hua)
中文导读
新型可重构线对称Goldberg 6R 机构
摘要：本文提出了一种新型可重构Goldberg 6R机构，它遵循异型串联Goldberg 6R机构的构造方法，同时又满足线对称Bricard条件。结合异构化的方法得到了这种新型可重构机理的异构化机构。特定的几何约束条件导致新型机构具有多个运动分支。基于雅可比矩阵的奇异值分解的方法，分析了在关节空间中机构的运动分支和分岔特性，推导出了机构在关节空间中的分岔原理图。该机构具有一个Goldberg 6R运动分支、两个线对称Bricard 6R运动分支和一个Bennett运动分支。对于线对称Bricard 6R运动分支，通过分岔重构为一种中间构型，可以实现与拆卸重组相同的功能。最后，用类似的方法对异构化机构进行了分析。利用机构的可重构性，沟通了两类过约束机构。
关键词：过约束机构；可重构机构；SVD方法；分岔特性
Foundation item: Projects(51535008, 51721003) supported by the National Natural Science Foundation of China; Project(B16034) supported by the Program of Introducing Talents of Discipline to Universities (“111 Program”), China
Received date: 2020-04-28; Accepted date: 2020-10-15
Corresponding author: WANG Rui-qin, PhD Candidate; Tel: +86-15122119625; E-mail: wruiqin@tju.edu.cn; ORCID: https://orcid.org/ 0000-0002-3087-3203
Abstract: This paper proposes a novel reconfigurable Goldberg 6R linkage, conformed to the construction of variant serial Goldberg 6R linkage, while simultaneously satisfying the line-symmetric Bricard qualifications. The isomeric mechanism of this novel reconfigurable mechanism is obtained in combination with the isomerization method. The geometrically constrained conditions result in variable motion branches of the mechanism. Based on the singular value decomposition of the Jacobian matrix, the motion branches and branch bifurcation characteristics are analyzed, and the schematics of bifurcations in joint space is derived. This novel 6R linkage features one Goldberg 6R motion branch, two line-symmetric Bricard 6R motion branches, and one Bennett motion branch. With regards to the line-symmetric Bricard 6R motion branches, a similar function for the disassembly and recombination process can be achieved by reconstructing an intermediate configuration through bifurcation. Then, the isomerized generalized variant Goldberg 6R linkage is explicated in a similar way. Acting as a bridge, reconfigurability connects two families of overconstrained mechanisms.
