
Thermodynamic properties and heat capacity of Ru metal in HCP, FCC, BCC and liquid state
PENG Hong-jian(彭红建)1, 2, ZHOU Jiao-lian(周姣连)1, XIE You-qing(谢佑卿)2
1. School of Chemistry and Chemical Engineering, Central South University, Changsha 410083, China;
2. School of Materials Science and Engineering, Central South University, Changsha 410083, China
Received 13 October 2009; accepted 25 May 2010
Abstract:
Isometric heat capacity cv and isobar heat capacity cp of Ru metal in HCP, FCC, BCC and liquid state were calculated by using pure element systematic theory. The results are in good agreement with joint army-navy-air force (JANAF) experimental value and the calculation result by first-principle (FP) method. But the results have great differences in contrast to Scientific Group Thermodata Europe (SGTE) database. The cause is found that it cannot neglect the electron devotion to heat capacity to adjust cp in one-atom (OA) method. The disparity between OA method and SGTE database was discussed. The main cause is that OA method adopts the crosspoint with iso-Ec-line and iso-a-line in hybritriangle to determine the properties, but SGTE database is obtained by extrapolation from activity measurements and critical assessment of data from a large number of binary system. Thermodynamic properties of Ru metal in HCP, FCC, BCC and liquid state, such as entropy S, enthalpy H and Gibbs energy G were calculated. Therefore, the full description of thermodynamic properties from 0 K to random temperature is implemented.
Key words:
Ru metal; heat capacity; thermodynamic property; OA method;
1 Introduction
Specific heat is an important physical quantity of thermodynamics, which is of great significance to multi-phase thermodynamic equilibrium calculations and alloy design. There are many methods[1-3], such as experimental evaluations and theoretic calculations, to get thermodynamic data of pure metals. In these multiple methods, the Scientific Group Thermodata Europe (SGTE) pure element database[4] collects thermodata above 298.15 K for 78 kinds of elements by using calculation phase diagram (CALPHAD). In order to keep the integrity of thermodynamic property of SGTE pure element database, XIE et al[5] constructed a framework of systematic sciences of alloy (SSA), which is constituted by systematic sciences of pure element, alloy physics and chemistry, and alloy statistic thermodynamics. The pure element one-atom (OA) method[6-12], which is the core content of systematic sciences of pure element, is implied to calculate heat capacity of Ru metal in HCP, FCC, BCC and liquid state. And the thermodynamic properties of Ru metal, such as entropy S, enthalpy H and Gibbs energy G were also calculated. The results are compared with results of SGTE database, experimental value of joint army- navy-air force (JANAF)[13], and the results calculated by first principle (FP) method.
2 Principles and methods
Generally, there is the following relations between isobar heat capacity cp and isometric heat capacity cv[14]:
cp=cv+TBVβ′2 (1)
![]() (2)
(2)
where T is the temperature; V is the molar volume, β′ is the coefficient of volume thermal expansion, and is got from model of Debye-Grüneisen: β′=3α; B is isothermal bulk modulus, and got from Eq.(2); θD is Debye temperature, kB is the Boltzman constant; r0 is the average effective bond length of the crystal in equilibrium; h is the Planck’s constant; m is the atomic mass; j is a multiple of half-wavelength; ε is the volumetric strain.
![]() (3)
(3)
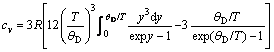 (4)
(4)
![]()
The relation among constant K, Q and microscopic quantity has been conducted by potential-energy function of many-atom interactions(MAI)[15]:
![]() (5)
(5)
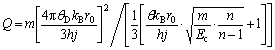 (6)
(6)
![]() (7)
(7)
With available heat capacity, other thermodynamic property can be calculated easily as follows:
![]()
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
where U is the internal energy, n is the potential energy
function MAI index, Ec is binding energy, ![]() is Debye temperature of natural state. In order to make the theoretical calculations and experimental values of isobar heat capacity cp in line better, some papers adopted the least squares method using (aT+bT 2+cT 3) to revise the theoretical value of isobar heat capacity cp[16], while the temperature coefficient thus obtained has no physical meaning. In order to obtain physically meaningful results, in this work another method was adopted. Debye model is also based on the heat capacity. The revised value of isobar heat capacity cp used the theoretical calculations to plus the contribution of electronic heat capacity, that was cp=
is Debye temperature of natural state. In order to make the theoretical calculations and experimental values of isobar heat capacity cp in line better, some papers adopted the least squares method using (aT+bT 2+cT 3) to revise the theoretical value of isobar heat capacity cp[16], while the temperature coefficient thus obtained has no physical meaning. In order to obtain physically meaningful results, in this work another method was adopted. Debye model is also based on the heat capacity. The revised value of isobar heat capacity cp used the theoretical calculations to plus the contribution of electronic heat capacity, that was cp=![]() + cv(e)=
+ cv(e)=![]() + γT, so isobar heat capacity cp obtained by this method is to be consistent with the experimental values well, then other thermodynamic properties can be calculated accordingly.
+ γT, so isobar heat capacity cp obtained by this method is to be consistent with the experimental values well, then other thermodynamic properties can be calculated accordingly.
3 Heat capacity of Ru metal
3.1 Heat capacity of Ru metal with HCP structure
Based on the above principles and methods, calculation results of isometric heat capacity cv and isobar heat capacity cp of HCP-Ru metal are shown in Fig.1. The results of FP method are shown in Fig.2. From Figs.1 and 2, isometric heat capacity cv calculated by OA method is in good agreement with calculating results by FP method, and the revised value of isobar heat capacity cp by OA method is in good agreement with the FP method and experimental value, but the result is quite different from the SGTE database. Compared with the OA method, the FP method can show contributions to heat capacity cv(e) made by electrons, which indicates the reason of OA method needs to be revised, that is, contributions to heat capacity cv(e) made by electrons cannot be neglected.
3.2 Heat capacity of Ru metal in FCC, BCC and liquid state
Isometric heat capacity cv and isobar heat capacity
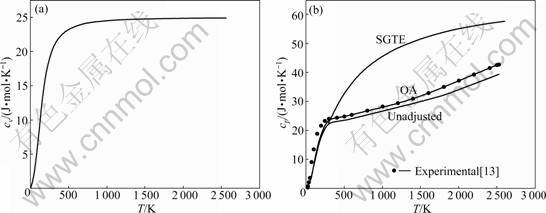
Fig.1 Curves of cv-T and cp-T of HCP-Ru metal calculated by OA method
cp for FCC, BCC and liquid of Ru pure metal are calculated by the same method and the results are shown in Figs.3-5. Isobar heat capacity cp by OA method in liquid state is in agreement with experimental value, but is quite different from the SGTE database. According to these figures, the results cannot be obtained by FP method at present, which differs greatly from SGTE database, especially at low temperature.
In OA method, the electronic structure of stable phase is determined by adopting the crosspoint with iso-Ec-line and iso-a-line in hybritriangle, then the physical and thermodynamic properties of element are
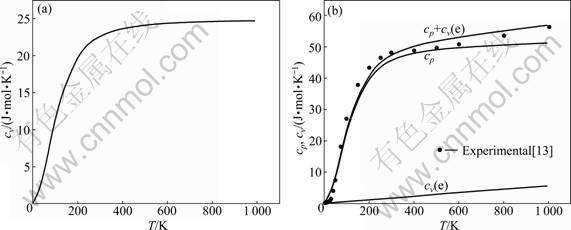
Fig.2 Curves of cv-T and cp-T of HCP-Ru metal calculated by FP method
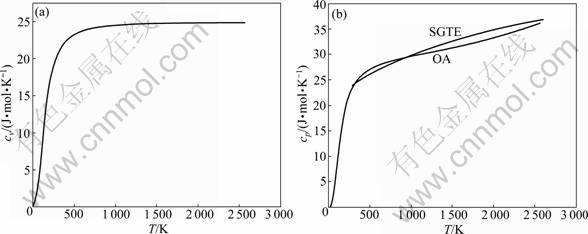
Fig.3 Curves of cv-T and cp-T of FCC-Ru metal calculated by OA method
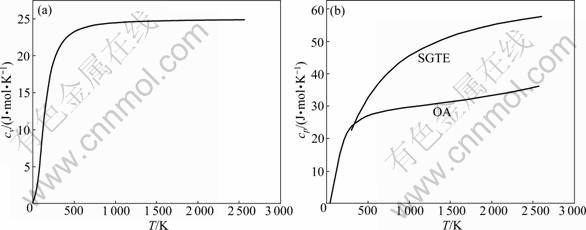
Fig.4 Curves of cv-T and cp-T of BCC-Ru metal calculated by OA method
determined. At the same time, the metastable phase electronic structure for the same element is also determined by adopting the crosspoint with iso-Ec-line and iso-a-line in the same hybritriangle. But, in the SGTE database, the relative Gibbs energy of different structures of pure metals, namely, lattice stabilization energy, is obtained by extrapolation from activity measurements and critical assessment of data from a large number of binary system, while for the other phase it is unstable. SGTE database does not take into account the Gibbs can be with the lattice constants and electronic structure of correlation. Therefore, OA method can implement the full description of the electronic structure of pure metal elements, and physical and thermodynamic properties from 0 K to random temperature, but SGTE can only implement the full description of thermodynamic properties from 298.15 K to random temperature. In addition, curves of cp-T by OA method emerges the broken line. Maybe it is the reason that the properties of element are determined to adopt consecutive functions by OA method.
4 Entropy, enthalpy and Gibbs energy as function of temperature
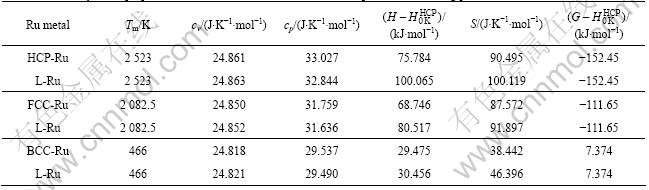
Taking the thermodynamic property of HCP-Ru at 0 K as referred value, which is SHCP=0, HHCP=650 kJ/mol [17], the thermodynamic property of HCP-, FCC-, BCC- and liquid-Ru can be changed as a function of temperature, as shown in Figs.6-9. From these figures, the results of thermodynamic properties, such as entropy S, enthalpy H and Gibbs energy G, are in good agreement with JANAF experimental values. Thermodynamic properties of stable and metastable phases by OA and FP method at 0 K are shown in Table 1. Comparing with SGTE database, it reinforces thermodynamic property of 0-298.15 K at low temperatures, and implements the full description of thermodynamic properties from 0 K to random temperature, making the information of pure metal more integral. At the same time, it can calculate the thermodynamic property of stable and metastable phases at its own melting point, as shown in Table 2.
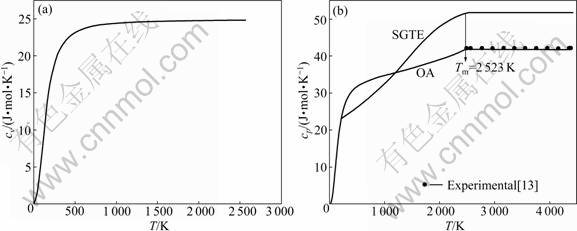
Fig.5 Curves of cv-T and cp-T of liquid-Ru metal calculated by OA method
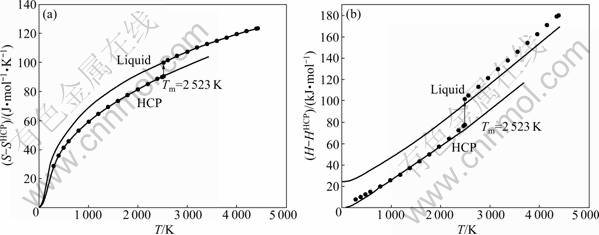
Fig.6 Curves of S-T (a) and H-T (b) of Ru metal in HCP structure and liquid state
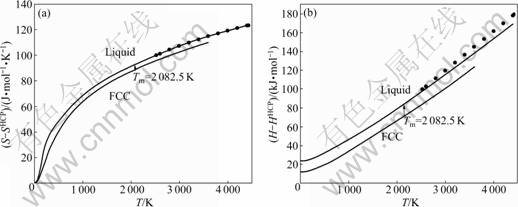
Fig.7 Curves of S-T (a) and H-T (b) of Ru metal in FCC structure and liquid state
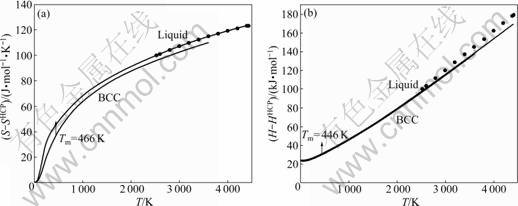
Fig.8 Curves of S-T (a) and H-T (b) of Ru metal in BCC structure and liquid state
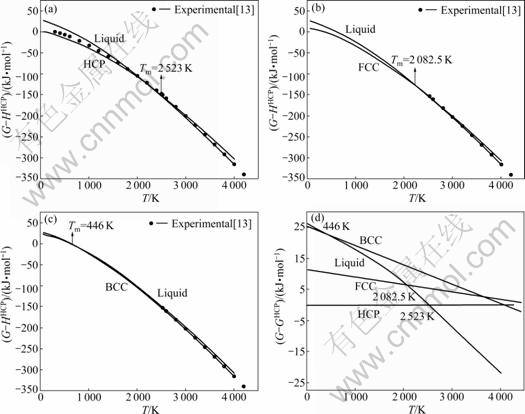
Fig.9 Curves of G-T of Ru metal in HCP (a), FCC (b), BCC (c) structure and liquid state and total Gibbs energy (d)
Table 1 Thermodynamic properties of Ru metal in HCP, FCC, BCC and liquid state at 0 K by OA and FP method in contrast to experimental value
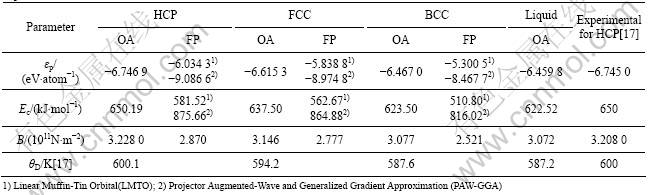
Table 2 Thermodynamic properties of Ru metal in HCP, FCC, BCC and liquid state at melting point
In Table 1, εp is the potential energy. Table 1 shows that the calculation result of lattice constant and cohesive energies are not consistent with each other by OA method and FP method except the order of stability: HCP>FCC>BCC. Other properties by OA method are in good agreement with experimental value.
5 Conclusions
1) Using pure element systematic theory, the specific heat of Ru metal with HCP structure was calculated. The results are in good agreement with JANAF experimental value and the calculation result by FP method, but the results have great differences in contrast to SGTE database. This indicates the reason of adjusting cp by OA method. The reason is that contributions to specific heat made by electrons cannot be neglected.
2) The heat capacity of Ru metal in FCC, BCC and liquid state was calculated, and the results also have great differences in contrast to SGTE database. The main cause is that OA method adopts the crosspoint with iso-Ec-line and iso-a-line in hybritriangle to determine the properties, but SGTE database is obtained by extrapolation from activity measurements and critical assessment of data from a large number of binary system.
3) Thermodynamic properties of Ru metal with stable and metastable phases such as entropy S, enthalpy H and Gibbs energy G from 0 K to random temperature were calculated, which are in good agreement with JANAF experimental value, making the information of pure metal more integral.
References
[1] SAUNDERS N, MIODOWIK A P, DINSDALE A T. Metastable lattice stabilities for the elements [J]. Calphad-Computer Coupling of Phase Diagrams and Thermochemistry, 1988, 12: 351-374.
[2] WANG Y, AURTAROLO S, JING C, ARROYAYE R, WANG T, CEDER G, CHEN L Q, LIU Z K. Ab initio lattice stability in comparison with CALPHAD lattice stability [J]. CALPHAD, 2004, 28(6): 79-90.
[3] ZHANG Z J. Calculation of the properties of some metals and alloys [J]. Journal of Physics: Condens Matter, 1998, 10(4): 495-499.
[4] DINSDALE A T. SGTE data for pure elements [J]. CALPHAD, 1991, 15(4): 317-425.
[5] XIE You-qing. The framework of metallic materials systematic science [J]. Mater Rev, 2001, 15(4): 12-15. (in Chinese)
[6] XIE Y Q, PENG K, LIU X B. Influences of xTi/xAl on atomic states, lattice constants and potential energy planes of ordered FCC TiAl type alloys [J]. Physica B, 2004, 344: 5-20
[7] XIE Y Q , LIU X B, PENG K, PENG H J, LI X B. Atomic states, potential energies, volumes, brittleness and phase stability of ordered FCC TiAl3 type alloys [J]. Physica B, 2004, 353: 15-33.
[8] XIE Y Q, PENG H J, LIU X B, PENG K, TAO H J. Atomic states, potential energies, volumes, brittleness and phase stability of ordered FCC Ti3Al type alloys [J]. Physica B, 2005, 362: 1-17.
[9] XIE Y Q, TAO H J, PENG H J, LIU X B, LI X B. Atomic states, potential energies, volumes, brittleness and phase stability of ordered FCC TiAl2 type alloys [J]. Physica B, 2005, 366: 17-37.
[10] TAO Hui-jin, XIE You-qing, PENG Hong-jian, LI Xiao-bo, NIE Yao-zhuang. Thermodynamic property of pure elemental Cu [J]. The Chinese Journal of Nonferrous Metals, 2006, 16(7): 1207-1213. (in Chinese)
[11] TAO Hui-jin, XIE You-qing, PENG Hong-jian, LI Xiao-bo, NIE Yao-zhuang. Thermodynamic property of fcc-Au and liquid–Au [J]. J Cent South Univ (Science and Technology), 2006, 37(16): 1036- 1042. (in Chinese)
[12] NIE Yao-zhuang, XIE You-qing, PENG Hong-jian, TAO Hui-jin, First-principles study of thermal properties of metal Ti [J]. J Cent South Univ (Science and Technology), 2007, 38(6): 1072-1077.
[13] CHASE M M. NIST-JANAF thermochemical tables (Fourth Edition, Part I) [M]. Gaithersburg: National Institute of Standards and Technology, 1998.
[14] ZHOU Ru-song. Solid physics [M]. Beijing: Higher Education Press, 1992: 105-107. (in Chinese)
[15] XIE You-qing. A new potential function with many-atom interactions in solid [J]. Science in China(Series A), 1993, 36(1): 90-99.
[16] OSTANIN S, SALAMATOY E. Effect of point defects on heat capacity of yttria-stablized zirconia [J]. Phys Rev B, 2003, 68(17): 2106-2109.
[17] GRAY D E. American Institute of Physics Handbook [M]. 3rd ed. New York: McGraw-Hill, 1972.
Foundation item: Project(50954006) supported by the National Natural Science Foundation of China; Project(2009GK3152) supported by Natural Science Foundation of Hunan Province, China; Project(21KZ) supported by Scientific Research Fund of Hunan Provincial Education Department, China; Project supported by the Opening Measuring Fund of Large Precious Apparatus, China; Project supported by the State Key Laboratory of Powder Metallurgy, China
Corresponding author: PENG Hong-jian; Tel: +86-731-88879287; E-mail: phj108@163.com
DOI: 10.1016/S1003-6326(09)60400-3


