Coupled mechanical and thermal simulation of warm compaction
LI Yuan-yuan(李元元)1, ZHAO Wei-bin(赵伟斌)2, ZHOU Zhao-yao(周照耀)1, CHEN Pu-qing(陈普庆)1
1. College of Mechanical Engineering, South China University of Technology, Guangzhou 510640, China;
2. Department of Computer Science, Guangdong Police Officers College, Guangzhou 510232, China
Received 21 March 2005; accepted 8 December 2005
Abstract:
Warm compaction process of pure iron powder was investigated. Due to the existence of elastic, plastic and thermal strains, a coupled mechanical and thermal model was applied. The elasto-plastic constitutive equations for powder material were developed based on ellipsoidal yield criterion and continuum theory. The constitutive equations were integrated into the constitutive integral arithmetic and solved employing incremental iterative solution strategy. The yield strength of iron powder was obtained according to the tensile experiments. When the compaction temperature was raised to 130 ℃, the yield strength of iron powder metal drops to 85% of room temperature value. Modified coulomb friction law is applied and the simulation results show that friction was an important factor resulting in the inhomogeneous relative density and reverse-density distribution phenomena in the regions near the die wall and the symmetrical axis.
Key words:
powder metal; warm compaction; finite element method; friction; relative density;
1 Introduction
Powder metallurgy is an advanced manufactural technology widely used for volume-producing mechanical parts with high performance and high precision[1-3]. Warm compaction is a low cost and effective technique to produce green compact with density higher than 7.5 g/cm3. Warm compaction also offers an approach to near-net-shape manufacturing.
As the main procedure in the powder metallurgy process, compaction forms the shape of the products. Therefore, it has a great effect on the precision and mechanical performance of them. The mechanical behavior of warm powder compaction involves complicated nonlinear phenomena, i.e., special nonlinear mechanical characteristics of powder material, large displacement and large strain, continuously changing contact condition between the metal powder and die, frictional force changing with relative density as well as the thermal effect due to plastic deformation or friction[4].
The study of powder metal compaction by numerical computation method can provide density and stress distribution during the processing. Compared with the empirical approach, numerical simulation offers a computational approach to reduce the time and cost for achieving proper tooling design and optimizing compaction parameters. Numerical simulation of warm powder compaction is based on continuum mechanical theory which treats the metal powders as a porous continuum.
In the past three decades, different kinds of Elliptical Cap yield models based on von MISES yield criterion have been deduced and investigated by researchers such as GREEN[5], KUHN and DOWNEY[6], SHIMA and OYANE[7] and DORAIVELU[8]. FLECK et al[9] proposed a micromechanical particle model based on FLECK model which was appropriate in the high porosity stage. GURSON model was usually used during the low porosity stage[10]. In the transition stage, REDANZ[11-14] developed a linear combination of Fleck and Gurson model. All these models mainly focused on cold powder compaction, while few studies had been focused on warm powder compaction.
The aim of this paper is to achieve a good numerical simulation of warm compaction. The elasto-plastic constitutive equations fit for powder material are developed obeying ellipsoidal yield criterion. The onstitutive equations are integrated into the constitutive integral arithmetic. A large displacement finite element method considering updated Lagrangian strategy is adopted to solve the coupled mechanical and thermal nonlinear problem.
2 Experimental
The comparison was performed using standard sintered samples (ISO 2740—1973). Initially, the thickness(C) was 6.0 mm and the length(Lc) was 32 mm. After elongation, C was 5.7 mm and Lc was 37 mm. The initial relative density of the tensile sample was approximately 89.7 %.
The tensile samples were prepared from highly compressible water atomized iron powder with particle size of 100-150 ?m. The mass of the specimen was kept constant at about 27 g. At least three other specimens were pressed afterwards under the same condition. Results show good reproducibility. The compacts were sintered at 1 120 ℃ for 2 h.
One edge of the sample was clamped which prevented rigid body motion of the sample. Another clamp (upper clamp) moved at a speed of 2 mm/min. The upper clamp was stopped when the sample was finally snapped. This occurred when the total displacement of the upper punch was 5 mm. During the deformation, the curve of the load versus the displacement was recorded by a microcomputer. The length of the sample increased, and the width reduced accordingly. The final overall dimensions were measured.
Fig.1 shows the stress—strain comparative curve of tensile experiment between cold and warm compaction. The tensile experiment shows that for iron based powder metals, the yield strength of porous metal in cold compaction was 135.4 MPa .When the temperature of warm compaction increases to 130 ℃, the yield strength of porous metal drops to 111.8 MPa, which is 85% was that at room temperature. For metal powders the curves of stress versus strain show a clear upward convexity and trend to flatten under a certain pressure.
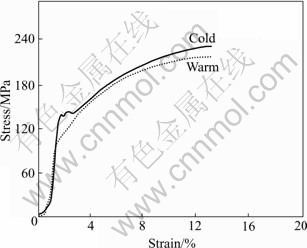
Fig.1 Stress—strain comparative curve of tensile experiment between cold and warm compaction
3 FEM simulation
3.1 Yield criterion
For ellipsoidal yield criterion with isotropy, yield function (F) can be written as
(1)
In the yield criterion deduced by KUHN and DOWNEY[6], A=2+R2, B=(1-R2)/3, C=
.
where 
and J1 are the second invariant of deviatoric stress component and the first invariant of stress tensor respectively. YR is the yield stress of the porous metals with relative density R. Y0 is the yield stress of non-porous metals. Rc is an experimental parameter corresponding to the critical relative density at which the yield stress of porous metal becomes zero.
Differentiating Eqn.(1) yields:
(2)
Hence
(3)
where A and B are state variants pertinent to the plastic strain 
, Y0 is a state variant pertinent to the plastic strain and the deformation temperature T.
In the case of associated plastic deformation, flow rule can be written as
(4)
Thus
(5)
σs is the function of temperature. If the temperature change is considered, then strain increment can be written as
(6)
The known relation between stain and stress is
Applying elastic stress—strain relation to elastic rigidity matrix changed with temperature, the stress increment becomes
(7)
According to Eqn.(6), the elastic stress—strain relation considering the temperature effect takes the form as
(8)
Compared with the elastic stress—strain relation ignoring the temperature effect, Eqn.(8) has two additional items, namely, initial strain 
and initial stress 
.
According to Eqns.(4), (5) and (8), Eqn.(2) can be rewritten as
(9)
Substituting Eqn.(3) and rearranging yields:
10)
Then Eqn.(8) revealing the incremental relation between stress and strain can be written as
(11)
where 
is defined as
(defined as plastic matrix ) has the form as
(12)
where thermal strain increment 
is defined as
3.2 Boundary conditions
With the densification of porous metals, the contact condition between the particles and the tooling changes with the relative density. The numerical simulation in this study supposed it follows the modified Coulomb principle, and is smoothed by arc-tangent function.
3.3 Numerical simulation
The finite element simulation analyzed a cylinder with a length of 90 mm, a radius of 20 mm. The mesh has 2 360 elements and 2 835 nodes. The whole compac- tion process is finished within 50 increments when the total displacement of upper punch is 33.78mm. The element type is an eight-node isoparametric, arbitrary hexahedral element. The user subroutine program adopts the yield strength from tensile experiment. The constitutive equations are integrated into the constitutive integral arithmetic and solved employing incremental iterative solution strategy. Simulation was carried out with MSC.Marc software. The elastic modulus of iron material was set at 200 GPa. Poisson ratio was 0.3. The upper punch, lower punch and die were treated as rigid bodies. The friction coefficient at the contact surfaces was set at 0.2. The contacts between the powder metals and between the powder metals and die wall were detected and processed. The maximum cycle number was set to be 10 000 and the tolerance was set to be 0.001[15].
4 Discussion
As shown in Fig.1, the yield strength of powder metal during warm compaction is 15% lower than that of room compaction. It can be inferred that moderate heating leads to increased green density under the same pressure. Fig.2 shows that compaction force of warm compaction is obviously lower than room compaction when the displacements are the same. As shown in Figs.3 and 4, Equivalent von MISES stress distribution of warm compaction ranges from 76.62 to 91.54 MPa. Equivalent von MISES stress distribution of cold compaction ranges from 91.56 to 110.2 MPa. The maximum Equivalent von Mises stress during warm compaction is 17% lower than room compaction. Moreover, the stress gradient of warm compaction is lower than cold compaction. When the powder metal is moderately heated, the increased atom activation energy partially eliminates the hardening effect of plastic deformation, which results in the decreased flow stress.
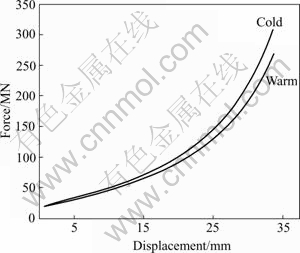
Fig.2 Force—displacement curve of upper punch of cold and warm compaction
Fig.3 Equivalent von MISES stress distribution of warm compaction
Fig.4 Equivalent von MISES stress distribution of cold compaction
In the initial stage of densification, corresponding to increment 1-10 of simulation results, the relative density decreases gradually from the upper to bottom in the regions near the die wall and vertical axis. While in the horizontal direction, the relative density distribution shows almost no difference. The high density gradient can only be observed in the intersecting regions between the die wall and the upper/lower surface. Therefore, the maximum and minimum relative densities exist in these regions.
In the densification stage, corresponding to increment 11-25, the density gradient of the regions near the die wall increases while the density gradient near the vertical axis becomes even. When the applied force continues to increase, corresponding to increment 26-35, the density gradient increases accordingly. On the vertical axis, reverse-density distribution phenomenon takes place compared with regions near the die wall. Also, the relative density gradient of porous metals in the horizontal direction increases with further densification. The subsequent increments maintain the increase tendency till the whole compaction process is finished.
During the early to middle period of compaction, the friction of die wall results in the inhomogeneous relative density of porous metals, while the friction of die wall has little effect on the regions near the vertical axis. The reverse-density distribution on the vertical axis mainly takes place during the middle to later period of compaction. During this period, the metal particles on the vertical section flow at the tendency from upper surface edge to lower surface center. Such kind of flowing tendency results in the high density area on the bottom.
Figs.5 and 6 display the relative density distribution of warm and cold compaction. As shown in the simulation result of density distribution change on the axial cross-section, friction on upper punch wall and die wall leads to the flowing tendency. Further study reveals that friction on upper punch wall prevents the metal particles in upper surface edge from moving to the center regions horizontally, so the particles flow leaning to the lower surface center according to plastic potential theory.
Fig.5 Relative density distribution of warm compaction
Fig.6 Relative density distribution of cold compaction
5 Conclusions
1) For iron based powder metals, when the temperature of warm compaction increases to 130 ℃, the yield strength of porous iron metal drops to 85% of room temperature value.
2) Friction plays an important role in particle flowing stage, which leads to the inhomogeneous relative density distribution.
3) In warm compaction, the relative density distribution of cylinder shows opposite tendency in the regions near the vertical axis and die wall due to the existence of friction of upper surface and die wall.
References
[1] Li Y Y, Ngai T L. Zhang D T, Long Y, Xia W. Effect of die wall lubrication on warm compaction powder metallurgy[J]. Journal of Materials Processing Technology, 2002, 129(1-3): 354-358.
[2] LI Yuan-yuan, ZHANG Da-tong, XIAO Zhi-yu, NGAI Tungwai Leo. Influence of high-energy ball milling on Al-30wt%Si powder and ceramic particulate[J]. Trans Nonferrous Met Soc China, 2000, 10(3): 324-327.
[3] CHEN Pu-qing, XIA Wei, ZHOU Zhao-yao, ZHU Quan-li, LI Yuan-yuan. Three-dimensional combined finite-discrete element approach for simulation of the single layer powder compaction process[J]. Trans Nonferrous Met Soc China, 2004, 14(8): 751-755.
[4] Sausa l c, Sa j c. Finite element modeling of thermo mechanical forming processes using a mixed method[A]. Numerical Methods in Industrial Forming Processes[C]. A.A. Balkena Rotterdam, 1992. 229-235.
[5] Green r j. A Plasticity theory for porous solids[J]. Int J Mech Sci Pergamon Press, 1972, 14: 215-224.
[6] Kuhn h a, Downey c l. Deformation characteristics and plasticity theory of sintered powder materials[J]. International Journal of Powder Metallurgy, 1971, 7(1): 15-25.
[7] Shima S, Oyane M. Plasticity theory for porous metals[J]. Int J Mech Sci, 1976, 18: 285-292.
[8] Doraivelu S M. A new yield function for compressible P/M materials[J]. Int J of Mech Sci, 1984, 26(9/10): 527-535.
[9] Fleck n a, Kuhn l t, McMeeking r m. Yielding of metal powder bonded by isolated contacts[J]. Journal of the Mechanics and Physics of Solids, 1992, 40: 1139-1162.
[10] Gurson a l. Continuum theory of ductile rupture by void nucleation and growth(part I): yield criteria and flow rules for porous ductile ductile media[J]. Journal of Engineering Materials and Technology, 1977, 99: 2-15.
[11] Redanz p. Numerical modeling of cold compaction of metal powder[J]. International Journal of Mechanical Sciences, 1998, 40(11): 1175-1189.
[12] Redanz p. Numerical modeling of the powder compaction of a cup[J]. Eur J Mech A/Solids, 1999, 18: 399-413.
[13] Redanz p. A study of stresses in powder compacted components during and after ejection[J]. International Journal of Solids and Structure, 2001, 38: 759-775.
[14] Redanz p, Tvergaard v. Analysis of shear band instabilities in compaction of powders[J]. International Journal of Solids and Structures, 2003, 40: 1853-1864.
[15] MSC Company. MSC.Marc 2000 User’s Guide [M]. Software Corporation, 2000. 255-257.
Foundation item: Project(50325516) supported by the National Foundation of China for Outstanding Young Scientists; Project(50135020) supported by the National Natural Science Foundation of China; Project(CG2003-GA005) supported by China Education and Research Grid (China Grid)
Corresponding author: ZHAO Wei-bin; Tel: +86-20-87112933; E-mail: vinsonzwb@21cn.com
Abstract: Warm compaction process of pure iron powder was investigated. Due to the existence of elastic, plastic and thermal strains, a coupled mechanical and thermal model was applied. The elasto-plastic constitutive equations for powder material were developed based on ellipsoidal yield criterion and continuum theory. The constitutive equations were integrated into the constitutive integral arithmetic and solved employing incremental iterative solution strategy. The yield strength of iron powder was obtained according to the tensile experiments. When the compaction temperature was raised to 130 ℃, the yield strength of iron powder metal drops to 85% of room temperature value. Modified coulomb friction law is applied and the simulation results show that friction was an important factor resulting in the inhomogeneous relative density and reverse-density distribution phenomena in the regions near the die wall and the symmetrical axis.
