Application of an analytical phase transformation model
LIU Feng (刘 峰), WANG Hai-feng(王海丰), YANG Chang-lin(杨长林), CHEN Zheng(陈 正),
YANG Wei(杨 伟), YANG Gen-cang(杨根仓)
State Key Laboratory of Solidification Processing,Northwestern Polytechnical University, Xi’an 710072, China
Received 20 April 2006; accepted 30 June 2006
Abstract:
Employing isothermal and isochronal differential scanning calorimetry, an analytical phase transformation model was used to study the kinetics of crystallization of amorphous Mg82.3Cu17.7 and Pd40Cu30P20Ni10 alloys. The analytical model comprised different combinations of various nucleation and growth mechanisms for a single transformation. Applying different combinations of nucleation and growth mechanisms, the nucleation and growth modes and the corresponding kinetic and thermodynamic parameters, have been determined. The influence of isothermal pre-annealing on subsequent isochronal crystallization kinetics with the increase of pre-annealing can be analyzed. The results show that the changes of the growth exponent, n, and the effective overall activation energy Q, occurring as function of the degree of transformation, do not necessarily imply a change of nucleation and growth mechanisms, i.e. such changes can occur while the transformation is isokinetic.
Key words:
Pd40Cu30P20Ni10; Mg82.3Cu17.7; metallic glass; phase transformation; heat treatment; crystal growth; calorimetry;
1 Introduction
For special cases of nucleation, the growth and impingement of the well-known analytical description of transformation kinetics holds, according to JOHNSON, MEHL and AVRAMI (JMA) [1-6]. Recently a more general modular, numerical kinetic model [7-9] has been proposed, taking the three mechanisms, nucleation, growth, and impingement of growing new phase particles, as entities that can be modeled separately. The model allows any type of time-temperature program and thus is also applicable to both isothermally conducted (time dependent) and isochronally conducted (temper- ature dependent) transformations. The kinetic model par- ameters, the growth (Avrami) exponent, n, the overall effective activation energy, Q, and the rate constant, K0, all depend on the operating nucleation and growth modes. Applying such a model to a phase transformation, it is assumed that throughout the temperature/time range of interest the transformation mechanism is the same (which is called “iso-kinetic”) and the kinetic parameters are assumed to be constant with respect to time and temperature [7-10].
Many experimental results of phase transformation kinetics have been reported and fitted with a JMA (-like) model. Often the measured kinetics cannot be described with constant values for n and Q within a JMA-like model (i.e. Refs.[11-13]): the fitted parameters, n and Q, are different for different stages of the transformation. This has been explained by corresponding, supposed changes in the nucleation and growth mechanisms [11-13], i.e. the transformation process would be not iso-kinetic. Fitting of JMA kinetics to such phase transformations therefore only yields a phenom- enological description. In principle, JMA kinetics is not applicable, if a mixture of nucleation mechanisms prev- ails. Eqn.(1) has been verified analytically only for the extreme conditions, i.e. for pure continuous nucleation or pure site saturation as nucleation mechanisms[10]. How- ever, it has been shown numerically that a JMA-like description provides a reasonable fit for intermediate cases, as transformations controlled by mixed nucleation or Avrami nucleation [8].
Against this background, an analytical model for solid-state phase transformations has been developed to incorporate the three mechanisms: nucleation (e.g. mixed nucleation and/or Avrami nucleation), growth(interface- controlled and/or volume diffusion controlled growth) and impingement [14, 15]. The model has been devel- oped for both isothermally and isochronally conducted transformations, with time or temperature dependent kinetic parameters (for which analytical descriptions have been given [14, 15]). On this basis Eqn.(1) has been analytically and generally validated: time/temperature dependencies on n and Q occur, but QN and QG are constant. Only for special cases, the model reduces to the well-known JMA description of transformation kinetics.
In the present work, the analytical model was used to study the crystallization kinetics of bulk amorphous Pd40Cu30P20Ni10 alloy and ribbons of melt-spun amorph- ous Mg82.3Cu17.7 alloy. From the fits of the analytical model to the experimental data obtained from isother- mally and isochronally conducted differential scanning calorimetry (DSC) experiments, the nucleation and growth modes occurring during the crystallization and the separate activation energies for nucleation and growth, were determined.
2 Phase transformation kinetics
2.1 Path variable for isothermal and isochronal transformations
It appears appropriate to introduce a path variable, b, which depends on the thermal history, i.e., the path followed in the temperature-time diagram: T(t) prescribes b [7]. The transformed fraction, f, depends on the path variable b through
(1)
The dependence of the path variable 
on the thermal history can be described as the integral over time of a rate constant K(T(t)), not conceived to be dependent on t other than through T:
(2)
where K is the rate constant. It follows from Eqn.(3) for isothermal annealing:
(3)
For many applications, K(T) can be given by an Arrhenius-type equation:
(4)
where Q is the overall, effective activation energy, K0 is a temperature and time-independent constant and R is the gas constant.
2.2 Modes of nucleation, growth, and impingement
The term site saturation was used in those cases where the number of (supercritical) nuclei does not change during the transformation: all nuclei, of number N* per unit volume, are already present at t=0:
(5)
where d(t-0) denotes the Dirac function.
The continuous nucleation rate per unit volume (i.e. the rate of formation of particles (nuclei) of supercritical size) is at large undercooling only determined by the rate of the jumping of atoms through the interface between the nucleus of critical size and the parent phase, which can be given by an Arrhenius term:
(6)
where N0 is a temperature-independent nucleation rate constant, and QN is the temperature- and time-independ-
ent activation energy for nucleation. The number of nuclei equals 0 at t=0.
The mixed nucleation mode involves that the nucleation rate is equal to some weighted sum of the nucleation rates according to continuous nucleation and site saturation:
(7)
where 
and N0 represent the relative contributions of the two modes of nucleation.
So-called Avrami nucleation involves that the rate of formation of supercritical nuclei at time t is given by Refs. [1-4, 8],
(8)
where λ is the rate at which an individual sub-critical nucleus becomes supercritical:
λ(t=τ)=λ0exp{-QN/[RT(τ)]}
with λ0 as a temperature-independent rate and N′as the total number of subcritical nuclei per unit volume at t=0.
The diffusion-controlled and the interface- control- ed growth modes can be given in a compact form. At time t, the volume Y of a particle nucleated at time τ is given by
(9)
where m is the growth mode parameter (m=1 for interface-controlled growth; m=2 for volume diffusion controlled growth) and d is the dimensionality of the growth (d=1, 2, 3), g is a particle-geometry factor and v(t)=v0exp{-QG/[RT(t)]} with QG as the temperature and time independent activation energy of growth.
For interface-controlled growth, v0 is a temperature- independent interface velocity constant and QG represents the energy barrier at the interface. For volume diffusion controlled growth, v0 equals the pre-exponent- ial factor for diffusion D0 and QG represents the activation energy for diffusion, QD .
The number of supercritical nuclei formed in a unit volume, at time τ during a time lapse dτ, is given by 
according to Eqns.(5-8). The volume of each of these nuclei grows from τ until t according to Eqn.(9) where it is supposed that every particle grows into an infinitely large parent phase, in absence of the other growing particles. In this hypothetical case, the volume of all particles at time t, called the extended volume, is given by
(10)
where V is the sample volume, which is supposed to be constant throughout the transformation.
In reality, the particles do not grow individually into an infinitely large parent phase: V e does not account for the overlap of particles (hard impingement) and their possible surrounding diffusion fields (soft impingement). It is supposed here that the nuclei are dispersed randomly throughout the total volume. Suppose that at time t the actually transformed volume is V t. If the time is increased by dt, the extended and the actual transformed volumes will increase by dV e and dV t. From the change of the extended volume dV e, only a part will contribute to the change of the actually transformed volume dV t, namely a part as large as the untransformed volume fraction [1-3, 6]. Hence,
(11)
Given the degree of transformation, f, this equation can be integrated as
(12)
2.3 General equation for the transformed fraction
According to Eqns.(5-10) and for cases of nucleat- ion considered here (as mixed nucleation and Avrami nucleation), the overall extended volume can be shown to be given by the addition of two parts: one part that can be conceived as due to pure site saturation and the other part to pure continuous nucleation. By extensive calculation an explicit analytical expression for the extended volume can be obtained [14, 15]. The degree of transformation can then be derived considering the impingement for example according to Eqn.(12).
No matter which of the nucleation or growth modes considered determine the transformation mechanism, the degree of isothermal or isochronal transformation can be uniquely described by combinations of the time dependent kinetic parameters: n(t), Q(t) and K0(t) (i.e. for isothermal transformation) or the temperature dependent kinetic parameters n(T), Q(T) and K0(T) (i.e. for isochronal transformation) as (see Tables 1-4 in Ref.[14] and Table 1 in Ref.[15] for corresponding expressions for n, Q, and K0),
(13)
where the kinetic parameters n, Q, and K0 depend on the time and temperature, and α can be identified with either the annealing time t for isothermal transformation, or with RT 2/F for isochronal transformation. The effective, overall activation energy, Q, can always be analytically interpreted as a combination of the activation energies for nucleation and growth, QN and QG,
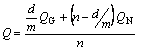(14)
In general, the kinetic parameters n, Q, and K0 are functions of time t (isothermal transformations) or
Table 1 Kinetic parameters as determined by fitting analytical phase transformation model to isothermal crystallization of amorphous Mg82.7Cu17.3
Table 2 Kinetic parameters determined by fitting analytical phase transformation model to isochronal crystallization of amorphous Pd40Cu30P20Ni10 with different pre-annealings for 600 s at different temperatures Tpre
temperature T (isochronal transformations), and are influenced by model parameters as N* and N0 (mixed nucleation) or
(Avrami nucleation), QN and QG, as well as annealing temperature T (isothermal trnasf- ormations) or heating rate F (isochronal transformations) [14]. Hence, the isokinetic transformation (section 1) does not necessarily require that, n, Q, and K0 have to be constants during the course of the transformation, as has very often been stated erroenously (i.e. Refs. [11, 13]). Obviously, the different combinations of nucleation and growth modes represent different transformation mechanisms, and result in different expressions for n(t), Q(t), K0(t) or n(T), Q(T), K0(T), and for the transformed fraction subjected to the general expressions Eqn.(13).
3 Specimens preparation and fitting proce- dure
The crystallization kinetics of amorphous melt spun ribbons of Mg82.3Cu17.7 was measured by recording isothermal DSC scans at temperatures of 356.7, 358.7, 360.7, and 362.7 K. The result of the influence of pre-annealing on the crystallization kinetics of bulk amorphous Pd40Cu30P20Ni10 alloy was investigated by performing isothermal pre-annealing at temperatures followed by recording isochronal DSC scans at heating rates (2.5, 5, 10, 20, 40 K/min). Experimental details regarding specimen preparation and the subsequent DSC analysis have been described in Refs. [10, 15]. The enthalpy change rates, dDH/dt or dDH/dT=(dDH/Fdt, isochronal scans) was obtained after the full baseline correction procedure [10].
Considering the nucleation modes and the growth modes as described in section 2.2, the following analytical models (combination of nucleation and growth mechanisms) have been fitted to the experimental data: (A) mixed nucleation and interface-controlled growth; (B) Avrami nucleation and interface-controlled growth; (C) mixed nucleation and volume diffusion controlled growth; (D) Avrami nucleation and volume diffusion controlled growth. The model parameters N* and N0 or
, QN and QG, were determined by fitting the analytical model, i.e. model A-D, to the dDH/dt or dDH/dT curves as obtained for either the various holding temperatures (i.e. isothermal annealing experiments) or the various heating rates (i.e. isochronal annealing exper- iments), simultaneously.
The fitting starts with an assumed set of initial values of N* and N0 or, QN and QG, as well as adopting one of the possible values of d/m (=3 or 3/2, if three dimensional growth is assumed). Substitution of values for these model parameters into Eqn.(13) allows to calculate the rate of enthalpy change, dDH/dt or dDH/dT. The least squares difference between the calculated dDH/dt or dDH/dT curves and those measured was minimized using a downhill simplex fitting proced- ure by altering the values for the four model parameters. The goodness of the fits (indicated as “error” in Tables 1-2) was calculated as the sum of the absolute differ- ences between the measured and the fitted dDH/dt or dDH/dT values, divided by the sum of the absolute valu- es of the fitted dDH/dt or dDH/dT values, of all curves fitted simultaneously.
4 Results and discussion
4.1 Fitting analytical models to isothermal annealing experiments
For Mg82.3Cu17.7, only model A based on mixed nucleation and interface-controlled growth, could be fitted well to the DSC results (Fig.1), giving a relative error of 10% (Table 1). Furthermore, the values obtained for N* and N0, 1016 m-3 and 4×1039 m-3?s-1 respectively (Table 1), are reasonable (cf. above discussion and Refs.[17-21]). In principle, the time dependent (Eqn.(13)) value of n, as calculated from the values of the model parameters obtained by fitting as function of the degree of transformation, was found to vary only from 3.9 to 4 for the whole range of isothermal transformation, which is compatible with almost pure continuous nucleation (as an extreme of the considered case of mixed nucleation) and interface-controlled growth. This interpretation is compatible with the lamellar microstructure of the trans-
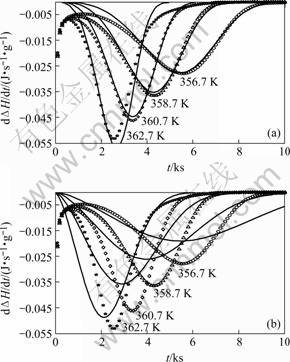
Fig.1 Rate of enthalpy change due to isothermal crystallization of amorphous Mg82.7Cu17.3, at different temperatures(symbols are measured values and as lines are fitted ones): (a) Interface-controlled growth; (b) Volume diffusion controlled growth, combined for both cases with mixed nucleation(For the fit, the initial part of the measurement, i.e. the first 1500 s has not been taken into account.)
formation product as observed by TEM, which suggests the occurrence of a eutectic, co-operative growth process of the two product phases, Mg2Cu and Mg [16].
4.2 Fitting analytical models to isochronal annealing experiments
The analytical models A to D were fitted to, simultaneously, the DSC curves recorded for isochronal anneals applied to amorphous Pd40Cu30P20Ni10 after sev- eral different pre-anneals (section 3.1). The results are shown in Table 2 and Fig.2.
Evidently, the models based on volume diffusion controlled growth, i.e. models C and D, provide good fits to the dDH/dT curves, in contrast with models A and B based on interface-controlled growth. Apparently, the isochronal crystallization is controlled by volume diffusion controlled growth, corresponding to particles precipitating in a matrix and with a composition different from that of the matrix (SEM observations discussed in Ref.[10]). Here, a detailed explanation (for model C) was solely given due to (text) space limitation.
Considering the results obtained by adopting mixed
Fig.2 Rate of enthalpy change divided by heating rate, dDH/Fdt=dDH/dT, due to isochronal crystallization of amor- phous Pd40Cu30P20Ni10, at heating rates indicated, as measured (symbols), and as fitted (lines), by assuming mixed nucleation and volume diffusion controlled growth (model(C)), after pre-annealing for 600 s at 623 K (a), 626 K (b) and 629 K (c)
nucleation, the values of N*, the number density of pre-existing nuclei, determined by fitting, increase from 1.1×1019 to 8.1×1021/m3 with increasing pre-annealing temperature, as should be expected. Also these numbers are physically realistic (section 4.1). The values obtained for N0, the temperature-independent nucleation rate, vary randomly in a small range from 2×1040 to 5×1041 m-3?s-1, i.e. N0 does not depend on the pre-annealing, as would be expected. Furthermore, the values obtained for N0 are physically realistic [17, 18].
As indicated by the increase of N* upon pre- annealing (model C), mixed nucleation, the initial state for the crystallization approaches the case of site saturation upon increasing the severity of the pre- annealing. Indeed, for model C, the values of n, calculated from the values of the model parameters obtained by the fitting as function of the degree of transformation, for the case of smallest degree of pre-annealing (600 s at 620 K) and the strongest degree of pre-annealing (600 s at 629 K), are constant and equal to 2.5 and 1.5. respectively (Table 2). Hence (Eqn.(9)), upon the increasing degree of pre-annealing, the character of the nucleation mode changes from largely continuous nucleation to largely site saturation. Further- more, the values determined for QN and QG or QD do not depend on the degree of pre-annealing, as should be expected, and are almost the same for both models (Table 2).
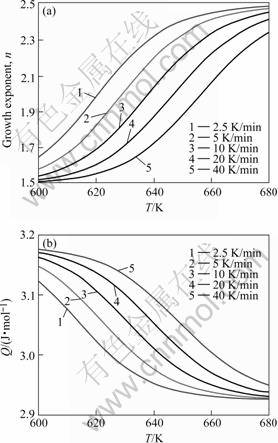
Fig.3 Growth exponent (a) and overall effective activation energy (b) as function of temperature for isochronal annealing at different heating rates of amorphous Pd40Cu30P20Ni10 after pre-annealed at 626 K for 600 s
The growth exponent n does not depend on the degree of transformation, if the continuous nucleation or site saturation prevails as nucleation mechanism. In these cases then also a constant value for the overall effective activation energy, Q, is resulted (Eqn.(14) and Table 2). This does not hold for intermediate cases of nucleation. In the case of mixed nucleation, the value of n is pronouncedly influenced by F and strongly depends on T (see the results shown in Fig.3). The potency of F to influence the value of n depends on the values of N* and N0. Because QN and QG or QD are constant indeed (Table 2), the value of Q as observed after a specific pre-annealing varies through n according to Eqn.(1), and thus depends on T and F (Fig.3). Similar results are obtained for the case of Avrami nucleation.
5 Conclusions
1) The analytical phase transformation model-incor-
porating as possible nucleation mechanisms and growth mechanisms: mixed nucleation (site saturation+ cont- inuous nucleation), Avrami nucleation and interface and volume diffusion-controlled growth-provides satisfactory description of the kinetics of crystallization of amor- phous Pd40Ni10P20Cu30 and Mg82.7Cu17.3 alloys.
2) The quality of the model fits to experimental isothermal and isochronal DSC scans and the evaluation of the values obtained for the (in all cases four) model parameters allows identification of the operating mech- anisms: isothermal crystallization of Mg82.7Cu17.3: mixed nucleation and interface-controlled growth; isochronal crystallization of Pd40Ni10P20Cu30: mixed nucleation or Avrami nucleation and volume diffusion-controlled growth.
3) For the first time it is shown experimentally that the changes of the growth exponent, n, and the effective overall activation energy Q, occurring as function of the degree of transformation, do not necessarily imply a change of nucleation and growth mechanisms, i.e. such changes can occur while the transformation is isokinetic. Constant values for n and Q occur only in extreme cases as site saturation and continuous nucleation.
4) The analytical phase transformation model allows determination of the separate values for the activation energies for nucleation and growth for a single set of isothermal or isochronal anneals for the same initial state of the material investigated. The separate values determined for the activation energies for nucleation and growth are found to be independent of the extent of pre-annealing, as it should be for an isokinetic transformation. No matter which kind of nucleation or growth mode prevails, the overall activation energy is always given by a combination of the constant activation energies for nucleation and growth according to Eqn.(14) which holds for isothermal and isochronal transformations.
Acknowledgement
The authors are grateful to Professor MITTEMEIJ- ER and Professor SOMMER for indispensable instruct- ion and cooperation and to Dipl.-Ing. H. NITSCHE in Max-Planck-Institute for Metals Research for support with the numerical calculations.
References
[1] JOHNSON W A, MEHL R F. Reaction kinetics in processes of nucleation and growth[]. Trans Am Inst Min (Metall) Engs, 1939, 135: 416-458.
[2] AVRAMI M. Kinetics of phase change(I): general theory[J]. J Chem Phys, 1939, 7: 1103-1112.
[3] AVRAMI M. Kinetics of phase change(II): transformation-time relations for random distribution of nuclei[J]. J Chem Phys, 1940, 8: 212-224.
[4] AVRAMI M. Granulation, phase change, and microstructure: Kinetics of phase change(III) [J]. J Chem Phys, 1941, 9: 177-184.
[5] KOLGOMOROV A N, AKA M. Kinetics of phase change[J]. Izv Nauk SSSR Ser Fiz, 1937, 3: 355-165.
[6] CHRISTIAN J W. The Theory of Transfomation in Metals and Alloys(Part 1). Equilibrium and General Kinetics Theory[M]. Oxford: Pergamon Press, 1975.
[7] MITTEMEIJER E J. Analysis of the kinetics of phase transformations[J]. J Mater Sci , 1992, 27: 3977-3987.
[8] KEMPEN A T W, SOMMER F, MITTEMEIJER E J. Determination and interpretation of isothermal and non-isothermal transformation kinetics: the effective activation energies in terms of nucleation and growth[J]. J Mater Sci , 2002, 37: 1321-1332.
[9] MITTEMEIJER E J, SOMMER F. Solid state phase transformation kinetics: a modular transformation model[J]. Metallkd Z, 2002, 93: 352-361
[10] KEMPEN A T W, SOMMER F, MITTEMEIJER E J. The isothermal and isochronal kinetics of the crystallisation of bulk amorphous Pd40Cu30P20Ni10[J]. Acta Mater, 2002, 50: 1319-1329.
[11] GHOSH G, CHANDRASEKARAN M. Delaey Isothermal crystallization kinetics of Ni24Zr76 and Ni24(Zr-X)76 amorphous alloys[J]. Acta Metall, 1991, 39: 925-936.
[12] NITSCHE H, SOMMER F, MITTEMEIJER E J. The Al nano-crystallization process in amorphous Al85Ni8Y5Co2[J]. Journal of Non-crystalline Solids, 2005, 351: 3760-3771.
[13] CALKA A, RADLINSKI A P. Dsc study of surface induced crystallization in Pd-Si metallic glasses[J]. Acta Mater, 1987, 35: 1823-1829.
[14] LIU F, SOMMER F, MITTEMEIJER E J. An analytical model for isothermal and isochronal transformation kinetics[J]. J Mate Sci , 2004, 39: 1621-1634.
[15] LIU F, SOMMER F, MITTEMEIJER E J. Parameter determination of an analytical model for phase transformation kinetics; application to crystallization of amorphous Mg-Ni alloys[J]. J Mater Res, 2004, 19(9): 2586-2596.
[16] KEMPEN A T W, NITSCHE H, SOMMER F, MITTEMEIJER E J. Crystallization kinetics of amorphous magnesium-rich magnesium- copper and magnesium-nickel alloys[J]. Metal Mater Trans, 2002, 33A: 1041-1050.
[17] JENA A K. Phase Transformations in Materials[M]. New Jersey: Englewood Cliffs, 1992.
[18] THOMPSON C V, GREER A L, SPAEPEN F. Crystal nucleation in amorphous (Au100-yCuy)77Si9Ge14 alloys[J]. Acta Metall, 1983, 31: 1883-1894.
[19] GREER A L. Crystallisation kinetics of Fe80B20 glass[J]. Acta Mater, 1982, 30: 171-192.
[20] ALLEN D R, FOLEY C J, PEREPEZKCO J H. Nanocrystal development during primary crystallization of amorphous alloys[]. Acta Mater, 1998, 46: 431-440.
[21] KELTON K F, PAEPEN F S. A study of the devitrification of Pd82Si18 over a wide temperature range[J]. Acta Metall, 1985, 33: 455-464.
Foundation item: Projects(50501020, 50395103) supported by the National Natural Science Foundation of China; Project(NCET-05-0870) supported by the New Century Excellent Person of China; Project supported by the Creative Foundation of Science and Technology of Youth in Northwestern Polytechnical University, China
Corresponding author: LIU Feng ; Tel: +86-29-88460374; Fax: +86-29-88492374; E-mail: liufeng@nwpu.edu.cn
[2] AVRAMI M. Kinetics of phase change(I): general theory[J]. J Chem Phys, 1939, 7: 1103-1112.
[5] KOLGOMOROV A N, AKA M. Kinetics of phase change[J]. Izv Nauk SSSR Ser Fiz, 1937, 3: 355-165.
[17] JENA A K. Phase Transformations in Materials[M]. New Jersey: Englewood Cliffs, 1992.
[19] GREER A L. Crystallisation kinetics of Fe80B20 glass[J]. Acta Mater, 1982, 30: 171-192.
