J. Cent. South Univ. Technol. (2010) 17: 830-835

DOI: 10.1007/s11771-010-0563-8

A novel weighted evolving network model based on clique overlapping growth

YANG Xu-hua(杨旭华)¹, WANG Bo(王波)^{1, 2}, SUN Bao(孙豹)¹

1. College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China;

2. Department of Computer Science and Engineering, Yiwu Industrial and Commercial College,

Yiwu 322000, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2010

Key words:

weighted network; clique overlapping; mean-field theory; bus transport network；

1 Introduction

Many practical complex systems in nature can be described by complex networks [1-3]. The research on complex networks originated from the small-world network model (WS model) proposed by WATTS and STROGATZ [4] and the scale-free network model (BA model) proposed by BARABASI and ALBERT [5]. In real world, evolving networks with different mechanisms have different characteristics. Constructing relevant network models for different kinds of networks is important for modeling and researching complex networks.

In most of real networks, one kind of collaboration networks has three distinct characteristics as follows. Firstly, this kind of networks expands continuously by addition of new cliques (maximal complete subgraph) [6-7], which is different from that of BA model expanding by the addition of new vertices [5]. Secondly, vertices of this network connect each other through intense overlapping of cliques. Thirdly, different edges between any two vertices of this network have different weights, and the bigger the weight, the closer the connection between two vertices. Many real networks belong to this kind of networks such as scientific collaboration network (SCN) [8-9], actor collaboration network (ACN) [10-11], Chinese medical prescriptions network (CMPN) [12-13] and bus transport network (BTN) [14]. In SCN or ACN, network expands by addition of new cliques (a paper or a movie) consisting of a few scientists (writing a paper together) or actors (acting a movie together). Cliques are overlapped intensely because there are some old existing scientists or actors in new cliques. The more the times two scientists or actors collaborate, the bigger the edge weight between them. In BTN described by space P [14], network also expands by the addition of new cliques (a bus route) consisting of a few stations (composing a bus route). There are old existing stations in new adding cliques. The more the bus routes between two stations are, the bigger the weight is; and the bigger the weight between two stations, the more convenient the transport.

Recently, many scholars have deeply studied this kind of collaboration network in various fields. PALLA et al [6] studied the overlapping communities character of scientific collaboration network, word-association and protein interaction graphs networks, and proposed k-clique community definition and corresponding clique percolation algorithm. GUIMERA et al [15] studied the effect of the team assembly mechanisms on the structure of the collaboration network and team performance. RAMASCO et al [16] studied collaboration networks in terms of evolving, self-organizing bipartite graph models and proposed a model of a growing network, which combines preferential edge selection with the bipartite structure, generic for collaboration networks. ZHOU et al [17] proposed an alternative model for collaboration networks based on nonlinear preferential selection. Depending on a single free parameter “preferential exponent”, this model interpolates between networks with a scale-free distribution and an exponential degree distribution. ZHANG et al [18] presented an empirical study on three non-social systems, which are the bus route networks of Beijing and Yangzhou, the travel route network of China, Huai—Yang recipes of Chinese cooked food, and a social system which is the collaboration network of Hollywood actors. And they suggested a simple model to show a possible evolutionary mechanism for the emergence of such networks. CHEN et al [19] presented the empirical investigation results on the urban bus transport networks of four major cities in China and introduced a model by which the analytic and numerical results agree well with the empirical facts. But all these involved models cannot represent the three characteristics completely and adequately. So, a weighted evolving network model based on the clique overlapping growth was proposed to represent these three characteristics of the collaboration network. According to mean-field theory, this model was analyzed theoretically under two different evolving mechanisms and the analytical results were obtained. And this model was used to get the simulation results. Finally, the practical bus transport networks of three major cities in China were investigated.

2 Presentation of weighted evolving network model

The model starts with clique c₀ consisting of m₀ vertices, and every edge weight is 1. In each time step new clique c_i consisting of m vertices (every edge weight is 1) is added. The new clique is composed of two parts

that contain some old vertices in the network and some new vertices. The numbers of the old vertices and the new vertices are m₁ and m₂, respectively. The edge weights are updated according to the equation:

                    (1)     

Two different selection mechanisms for the old vertices in a new clique were considered.

(1) Preferential selection mechanism. Probability p_i that an old vertex i is selected into the new clique depends on the number of cliques h_i that the vertex is joined. p_i can be expressed as

                                      (2)

(2) Random selection mechanism. Old vertex i will be randomly selected from those vertices that were added at previous time steps.

Fig.1 shows the evolution of the model when m₀= m=4, m₁=m₂=2. At initial time t=0, the initial network is a clique consisting of four vertices, and every edge weight is 1. In each time step a new clique consisting of four vertices is added. Two vertices in the new clique are selected from those vertices which were added at previous time steps by one of the selection mechanisms stated above. The other two vertices are newly added vertices. And the edge weights update according to Eq.(1).

3 Distributions of h_i and s_i

In this section, distributions of h_i and the vertex strength s_i of the evolving model under two different mechanisms were studied by simulations and analyses on the basis of mean-field theory.

3.1 Preferential selection mechanism model

First, the model was analyzed and simulated under preferential selection mechanism. Here, h_i means the number of cliques that a vertex joins and s_i means the vertex strength (similar to the degree in unweighted

networks, the vertex strength exhibits the vertex properties well in weighted networks) [20-22]. The formula of the vertex strength is

                            (3)    

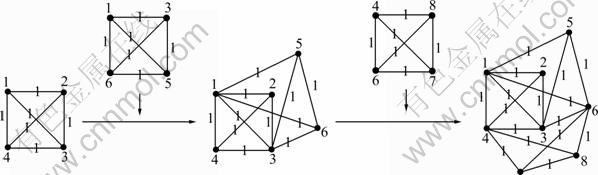
Fig.1 Evolution process of model (m₀=m=4, m₁=m₂=2)

According to mean-field theory [5, 23], in each time step if vertex i is selected into the new adding clique, h_i will be increased by one. The evolution equation of h_i using a quasi-continuous approximation can be described as follows:

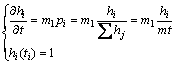               (4)     

The solution of this equation is h_i(t)=(t/t_i)^β, where β=m₁/m is called dynamical exponent.

To get the distribution of h_i, the equations are transformed as follows:

                    (5)

          (6)   

                     (7)

Eq.(7) is the distribution function of the number of cliques that vertex i joins (h_i). Besides, obviously s_i= h_i(m-1). Then, the vertex strength distribution can be obtained:

       (8)  

So, both of the distributions of h_i and s_i (P(h) and P(s)) follow the scale-free power-law distribution, whose power-law exponents are the same value of -(1/β+1)= -(m+m₁)/m₁.

Figs.2 and 3 show the simulation results of the distributions of the number of cliques that a vertex joins and vertex strength, respectively. Two cases of the model where m₀=m=4, m₁=m₂=2 and m₀=m=4, m₁=3, m₂=1 are shown in Figs.(a) and (b), respectively. And the number of vertices of the model is N=10 000. The slopes of the solid lines are the analytical results which are -3.000 0 in (a) and -2.333 0 in (b). The data of Figs.2 and 3 show that both P(h) and P(s) follow the scale-free power-law distribution, and the simulation results are in agreement with the analytical results well. As our analytical results are the statistical results when t→∞, there is a small deviation between the simulation results and the analytical results. The larger the vertex number of the model is, the more accordant the simulation results and the analytical results are.

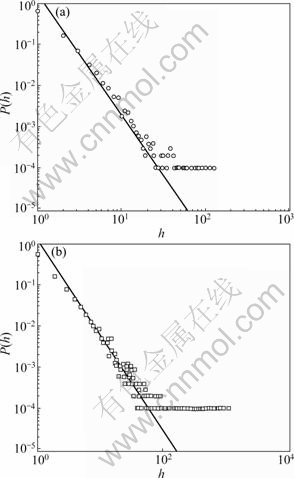
Fig.2 Distribution of number of cliques that vertex joins under preferential selection: (a) m₀=m=4, m₁=m₂=2; (b) m₀=m=4, m₁=3, m₂=1

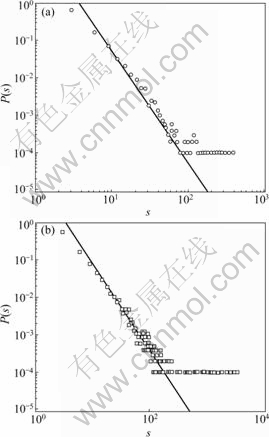
Fig.3 Distribution of vertex strength under preferential selection: (a) m₀=m=4, m₁=m₂=2; (b) m₀=m=4, m₁=3, m₂=1

3.2 Random selection mechanism model

In the process of evolving, m₁ old vertices are selected randomly from the vertices created at previous time steps. The evolution equation of h_i can be described as follows by using the same quasi-continuous approximation:

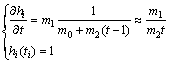                       (9)

The solution is

 or            (10)

The equations were transformed as follows:

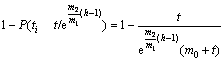       (11)

            (12)

                (13)

Eq.(13) is the distribution function of the number of cliques that vertex i joins (h_i). To see the relation between P(h) and h clearly and easily, Eq.(13) is transformed as:

                  (14)

Besides, s_i=h_i(m-1). So

                (15)

or

                 (16)

Both of the distributions of h_i and s_i (P(h) and P(s)) follow the exponential distribution, whose exponents are -m₂/m₁ and -m₂/[m₁(m-1)], respectively.

The simulation results of the distributions of the number of cliques that a vertex joins and vertex strength are shown in Figs.4 and 5, respectively. Two cases of the model where m₀=m=4, m₁=m₂=2 and m₀=m=4, m₁=3, m₂=1 are shown in (a) and (b), respectively. And the number of vertices of the model is also 10 000. The slopes of the solid lines which are the analytical results in Figs.4(a) and (b) are -0.434 3 and -0.144 8, respectively, while in Figs.5(a) and (b) those are  -0.144 8 and -0.048 3, respectively. The data of Figs.4 and 5 show that both P(h) and P(s) follow the exponential distribution, and the simulation results are in good agreement with the analytical results. The same to the evolving model under preferential selection mechanism, with the increase of the vertex number of the model the simulation results and the analytical results will be more accordant.

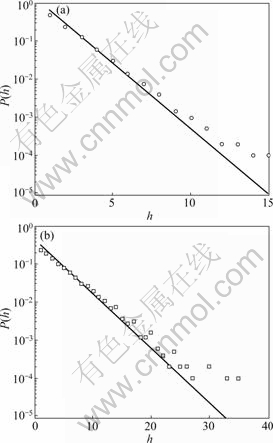
Fig.4 Distribution of number of cliques that vertex joins under random selection: (a) m₀=m=4, m₁=m₂=2; (b) m₀=m=4, m₁=3, m₂=1

4 Empirical study on BTNs

In order to verify that the model can simulate certain kind of collaboration networks, the practical bus transport networks (BTNs) of three major cities in China, which are Beijing, Shanghai and Hangzhou, were analyzed. The three practical BTNs were described in space P [14], which means that one vertex represents one station, and one edge represents one link between two stations if there is at least one bus route which serves the two stations. The edge weight between two vertices is defined as the number of bus routes between the two stations. The distributions of the number of bus routes (cliques) that a station (vertex) joins (P(h)) and the station (vertex) strength (P(s)) can be obtained. In order to reduce large statistical fluctuations, the cumulative distributions P(h_i＞h) and P(s_i＞s) were used to describe distributions P(h) and P(s) [14].

Fig.5 Vertex strength distribution under random selection:    (a) m₀=m=4, m₁=m₂=2; (b) m₀=m=4, m₁=3, m₂=1

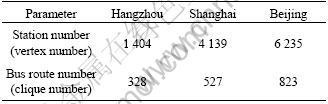
The basic information of three BTNs is listed in Table 1. Figs.6 and 7 show the empirically obtained cumulative distributions of the number of bus routes that a station joins (P(h)) and the station strength (P(s)) in the three practical BTNs, respectively. The statistical data of the three practical BTNs are obtained from Internet [14].

Table 1 Basic information of three practical BTNs

In Figs.6 and 7, most of the data fall on the linear lines on the single-logarithmic plane, which means that the cumulative distributions in two figures can be presented as two exponential functions, respectively:

 ＞0 and  is a constant        (17)

 ＞0 and  is a constant         (18)

The two cumulative distributions are very similar to those of the model under random selection mechanism in section 3.2 where both P(h) and P(s) have the characters of exponential function. From this viewpoint, for practical BTNs, a possible explanation was given as follows: the practical BTN is a kind of weighted evolving network based on the clique overlapping growth and the random selection is its main evolving manner.

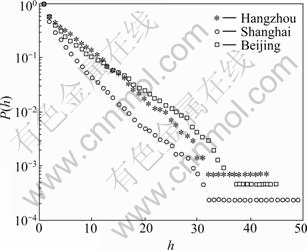
Fig.6 Cumulative distribution of number of bus routes that station joins in three practical BTNs

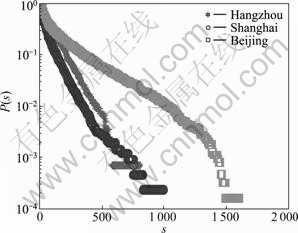
Fig.7 Cumulative station strength distribution of three practical BTNs

The BTNs are the primary carriers of the urban passenger flow in China currently. The research on BTNs’ models can give positive opinion to BTNs’ allocation plan and dynamic problem, and will be helpful for raising the carrying capacity and service performance of the whole road networks. This also indicates that the research content can simulate certain practical networks very well.

5 Conclusions

(1) Under different selection mechanisms, the model exhibits different network characteristics. The results show that under preferential selection mechanism both distributions P(h) and P(s) follow a scale-free power-law distribution whose exponents are -(m+m₁)/m₁, while under random selection mechanism both follow two exponential distributions with exponents -m₂/m₁ and -m₂/[m₁(m-1)], respectively.

(2) For three real BTNs, which are Beijing, Shanghai and Hangzhou, the cumulative distributions of the number of bus routes that a station joins and the station strength were studied. The two cumulative distributions are very similar to those distributions of the model under random selection mechanism proposed in this context where both P(h) and P(s) have the characters of exponential function. From this viewpoint, a possible explanation for practical BTNs is given as follows: the practical BTN is a kind of weighted evolving network based on the clique overlapping growth and random selection is its main evolving manner. This also indicates that the model can simulate certain practical networks very well and has practical significance.

(3) This model is a simplification of practical networks. It captures all the main characteristics of the kind of collaboration networks mentioned and clearly exhibits this kind of networks’ evolving mechanisms, evolving processes, and evolving results.

References

[1] ALBERT R, BARABASI A L. Statistical mechanics of complex networks [J]. Review of Modern Physics, 2002, 74(1): 47-97.

[2] NEWMAN M E J. The structure and function of complex networks [J]. SIAM Review, 2003, 45(2): 167-256.

[3] ZHOU Tao, BAI Wen-jie, WANG Bing-hong, LIU Zhi-jing, YAN Gang. A brief review of complex networks [J]. Physics, 2005, 34(1): 31-36.

[4] WATTS D J, STROGATZ S H. Collective dynamics of ‘small-world’ networks [J]. Nature, 1998, 393(6684): 440-442.

[5] BARABASI A L, ALBERT R. Emergence of scaling in random networks [J]. Science, 1999, 286(5439): 509-512.

[6] PALLA G, DERENYI I, FARKAS I, VICSEK T. Uncovering the overlapping community structure of complex networks in nature and society [J]. Nature, 2005, 435(7043): 814-818.

[7] DERENYI I, PALLA G, VICSEK T. Clique percolation in random networks [J]. Physical Review Letters, 2005, 94(16): 160202.

[8] CARDILLO A, SCELLATO S, LATORA V. A topologic analysis of scientific coauthor ship networks [J]. Physica A, 2006, 372(2): 333-339.

[9] TOMASSINI M, LUTHI L. Empirical analysis of the evolution of a scientific collaboration network [J]. Physica A, 2007, 385(2): 750-764.

[10] HE Nan, GAN Wen-yan, LI De-yi, KANG Jian-chu. The topological analysis of a small actor collaboration network [J]. Complex Systems and Complexity Science, 2006, 3(4): 1-10.

[11] LIU Ai-fen, FU Chun-hua, ZHANG Zeng-ping, CHANG Hui, HE Da-ren. An empirical statistical investigation on Chinese mainland movie network [J]. Complex Systems and Complexity Science, 2007, 4(3): 10-17.

[12] HE Yue, ZHANG Pei-pei, TANG Ji-ying, HAN Xue-fang, QIU Rong, CHEN Qi-juan, ZHOU Yue-ping, CHANG Hui, HE Da-ren. A collaboration network description on traditional Chinese medical prescription formulation system [J]. Science and Technology Review, 2005, 23(11): 36-39.

[13] CHANG Hui, SU Bei-bei, ZHOU Yue-ping, HE Da-ren. Assortativity and act degree distribution of some collaboration networks [J]. Physica A, 2007, 383(2): 687-702.

[14] YANG Xu-hua, WANG Bo, WANG Wan-liang, SUN You-xian. Research on some bus transport networks with random overlapping clique structure [J]. Communications in Theoretical Physics, 2008, 50(5): 1249-1254.

[15] GUIMERA R, UZZI B, SPIRO J, AMARAL L A N. Team assembly mechanisms determine collaboration network structure and team performance [J]. Science, 2005, 308(7722): 697-702.

[16] RAMASCO J J, DOROGOVTSEV S N, PASTOR-SATORRAS R. Self-organization of collaboration networks [J]. Physical Review E, 2004, 70(3): 036106.

[17] ZHOU Tao, WANG Bing-hong, JIN Ying-di, HE Da-ren, ZHANG Pei-pei, HE Yue, SU Bei-bei, CHEN Kan, ZHANG Zhong-zhi, LIU Jian-guo. Modelling collaboration networks based on nonlinear preferential selection [J]. International Journal of Modern Physics C, 2007, 18(2): 297-314.

[18] ZHANG Pei-pei, CHEN Kan, HE Yue, ZHOU Tao, SU Bei-bei, JIN Ying-di, CHANG Hui, ZHOU Yue-ping, SUN Li-cheng, WANG Bing-hong, HE Da-ren. Model and empirical study on some collaboration networks [J]. Physica A, 2006, 360(2): 599-616.

[19] CHEN Yong-zhou, LI Nan, HE Da-ren. A study on some urban bus transport networks [J]. Physica A, 2007, 376: 747-754.

[20] WANG Wen-xu, WANG Bing-hong, HU Bo, YAN Gang, OU Qing. General dynamics of topology and traffic on weighted technological networks [J]. Physical Review Letter, 2005, 94(18): 188702.

[21] BARRAT A, BARTHELEMY M, VESPIGNANI A. Weighted evolving networks: Coupling topology and weight dynamics [J]. Physical Review Letters, 2004, 92(22): 228701.

[22] BRAUNSTEIN LA, WU Z, CHEN Y, BULDYREN SV, SREENIVASAN S, KALISKY T, COHEN R, LOPEZ E, HAVLIN S, STANLEY HE. Optimal path and minimal spanning trees in random weighted networks [J]. International Journal of Bifurcation and Chaos, 2007, 17(7): 2215-2255.

[23] BARABASI A L, ALBERT R, JEONG H. Mean-field theory for scale-free random networks [J]. Physica A, 1999, 272(1/2): 173-187.

Foundation item: Projects(60874080, 60504027) supported by the National Natural Science Foundation of China; Project(20060401037) supported by the National Postdoctor Science Foundation of China

Received date: 2009-11-07; Accepted date: 2010-04-01

Corresponding author: YANG Xu-hua, PhD, Associate professor; Tel: +86-571-85290519; E-mail: xhyang@zjut.edu.cn

(Edited by LIU Hua-sen)