Solute trapping model based on solute drag treatment
WANG Hai-feng(王海丰), LIU Feng(刘 峰), CHEN Zheng(陈 正), YANG Wei(杨 伟)
State Key Laboratory of Solidification Processing, Northwestern Polytechnical University, Xi’an 710072, China
Received 26 November 2008; accepted 29 June 2009
Abstract:
A solute trapping model is developed based on a so-called solute drag treatment. By adopting a basic approach of phase-field models, and defining the free energy density in the interfacial region, a suitable interface shape function is introduced to derive the current model, in which the equilibrium and non-equilibrium interface behaviours can be described using a dimensionless parameter L (i.e. an important parameter in the present interface shape function). When applying the current model to Si-9%As (molar fraction) alloy with L=0.5, a good prediction of the steeper profile for high interface velocity, which is analogous to that using a phase-field model of DANILOV and NESLTER, has been obtained.
Key words:
solute trapping; solute drag; diffusive interface;
1 Introduction
Solute trapping has been extensively studied since a phenomenon that the solid cadmium concentration in zinc-cadmium alloys could extend the equilibrium solid solubility limit after splat quenching was observed[1]. It is defined as “solute trapping” because the solute atoms seem to be caught by the growing phase although there is a driving force for them to escape from[2], and this phenomenon is broadly studied in pulsed laser annealing experiments[3-6]. So far, solute trapping has been theoretically treated using sharp interface methods[7-12], phase-field methods[13-16] and solute drag methods[17-18].
For sharp interface models, a discontinuity of solute concentration occurs at the interface. Whereas, the phase-field models consider, in a more realistic way, a diffusive interface with a finite thickness and describe dynamic phenomena in both the bulk phases and the interface region in terms of a single formalism. The interface properties change as a function of the phase-field variable φ (φ=1 for one phase and φ=0 for the other one) and the variation of φ with distance through the interface is determined by a step-wise, local minimization of Gibbs energy in a finite-element procedure[2]. The concentration profile becomes a continuous function of the coordinate. The specific jump in the concentration at the interface which is typical for a sharp interface formulation disappears and is replaced by a continuous profile with a characteristic maximum near the transition region[16]. As for the solute drag models, a finite thickness of the interface is also assumed, which is similar to the phase-filed models. However, it is supposed that the diffusivities and thermodynamic properties change only as functions of distance through the interface.
Compared with the sharp interface models without considering interfacial solute diffusion and the complicated phase-field models, the solute drag treatment gives a relatively simple expression incorporating interfacial solute diffusion. However, the solute drag treatment is generally based on the wedge-shaped[17-18], truncated wedge[19-21] or smooth interface[22]. The above so-called continuous interface models are not really continuous[2]. The solute concentration profile across the interface to the bulk phases changes only continuously but not smoothly, i.e. the diffusive function cannot be described by a uniform formalism.
In the present work, a suitable interface shape function is introduced using a basic approach with of phase-filed models, that the free energy density of the interfacial region incorporated with the solute drag treatment. On this basis, a relatively simple solute trapping model, with characteristics analogous to phase-field approaches, is obtained.
2 Model derivation
2.1 Interface solute diffusion and solute trapping
For a binary system, i.e. solvent A and solute B, a layer of thickness, δ, exists between liquid and solid phases, where the thermodynamic quantities, such as the solute chemical potential, μB, change continuously from solid to liquid. Supposing an ideal solution, μB in the interfacial region can be given as
(1)
where
is the standard chemical potential of the solute, R the gas constant, TI the interface temperature and C the solute concentration which depends on the coordinate X normal to the moving interface.
Then, the diffusive flux of the solute, J, can be given as
(2)
where Vm is the molar volume, and DI the solute diffusion coefficient which also changes continuously from solid to liquid across the interface.
Given a constant V, the composition profile in the interface is expected to reach a steady state. Supposing that the solid-state solute diffusion is always omitted, the mass conservation law gives
(3)
where CS is the solid concentration adjacent to the interface, and is expected to be C0 under steady state. From Eqs.(2) and (3), solute diffusion in the interface can be described as
(4)
The solution of Eq.(4) can be expressed as
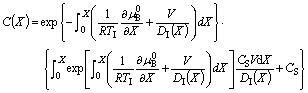(5)
As compared with CAHN’s model [18], Eq.(5) presents no singularity for V=0, since the solute diffusion in the solid is not considered here. Following the normal procedure of the solute drag treatment[17], the non-equilibrium partition coefficient, k, can be deduced as
(6)
In terms of η=X/δ, then Eqs. (5) and (6) reduce to
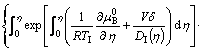
(7)
and
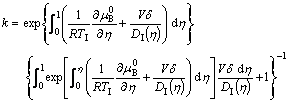
(8)
Eq.(8) is the general expression for solute trapping in a dilute alloy, obtained from the solute drag treatment. It is clearly shown in Eq.(8) that solute trapping is only influenced by interface diffusion if V is already known. If V=0, an equilibrium interface holds, then interface diffusion is solely determined by the gradient of the standard chemical potential 
and the non-equilibrium partition coefficient reduces to the equilibrium one, ke. If V→∞, then interface diffusion is solely determined by V/DI in Eq.(7) or (8), and a complete solute trapping occurs. This coincides with the limiting condition proposed by BAKER for the solute trapping model.
2.2 Interface shape function
In the solute drag treatment, the interface shape function, i.e. the diffusivities and thermodynamic properties as functions of the distance (i.e. η in Eqs.(7) and (8)) through the interface, are given as a priority. In order to obtain the interface solute concentration, C(η), and the non-equilibrium partition coefficient k for a given V, and DI(η) in Eqs.(7) and (8) should be known. Generally, different interface shape functions lead to different solute trapping models. Given a wedge-shaped interface function for 
DI(η) can be assumed, respectively, as the solid-state diffusion coefficient, DS, for half of the interface adjacent to the solid, and as the liquid-state diffusion coefficient, DL, for half of the interface adjacent to the liquid. Then, Eq.(8) reduces to BAKER’s model[17]. Assuming a linear change of 
and a constant DI(η) in the interface, Eq.(8) reduces to the vacancy trapping model of HILLERT et al[23]. Furthermore, a combination of smooth shape interface function for 
and constant DI assumption as the treatment of SVOBODA et al[22], or other treatments, for example truncated wedge interface[19-21], will lead to another solute trapping model.
However, the above treatments guarantee only a continuous but not smooth solute concentration profile across the interface to the bulk phases, i.e. the interface is not really continuous. In order to obtain a diffusive interface under steady state, the standard chemical potential should change not only continuously but also smoothly from the interface to the bulk liquid. If fulfills the following condition:
(9)
and also, if the diffusion coefficient DI changes continuously from solid to liquid across the interface, then the steady-state interface diffusion function (i.e. Eq.(4)) will change continuously from the interface to the bulk liquid where there is no standard chemical potential gradient, i.e. the solute diffusion in the liquid and the interface can be described by a uniform formalism. By adopting a basic approach of the phase-field models[15], with defining the free energy density in the interfacial region, a simple expression for is
(10)
where
and
are the standard chemical potentials of liquid and solid, respectively. The dimensionless parameter, L, which determines the characteristics of the interface, is assumed to be a constant value. Compared with phase-field models where the interface properties are dependent on the phase-field variable, φ, the interface properties in Eq.(10) are determined by the distance η. The term η2(3-2η) comes from the function h(φ)=φ2(3-2φ), which is monotonic in the interface, and the term η2(1-η)2 comes from the double-well potential g(φ)= φ2(1-φ)2 in the phase-field model[15].
Further, it is better that ?DI(η)/?η fulfills the following condition below. To obtain a diffusive interface, such condition is not necessary under steady state condition, but it must be fulfilled under non-steady condition[24]:
(11)
Since it is assumed in the present model that DI(η) changes monotonic as a function of η, an expression for DI(η) is then obtained according to h(φ)=φ2(3-2φ) in the phase-field model[15]:
(12)
Until now, one can see that the interface shape function was deduced using phase-filed approach[15] and the interface characteristic is described in terms of a double-well potential function with a dimensionless parameter, L.
Further, can be obtained from Eq.(10) as
(13)
Note that 
=RTIlnke, then substitution of Eqs.(10) and (13) into Eqs.(7) and (8) gives the following equations:
(14)
(15)
Now, a solute trapping model incorporating diffusive interface is obtained, as well as the solute composition profile is across the interface. Obviously, this is a relatively simple analytical expression, with characteristics analogous to phase-field approaches because the interface shape function is deduced from the defining the free energy density in the interfacial region of phase-field model[15] and the solute diffusion in the liquid and the interface can be also described by a uniform formalism, which is also the characteristic of the phase-field model. As shown in Eqs.(10) and (13), L is an important parameter, which plays an analogous role to EB (i.e. the solute interaction energy at the center of the interface) from BAKER’s solute trapping models[17], or to A (i.e. an additional potential term for determining the equilibrium interface characteristics) from the smooth interface model[22]. Under equilibrium condition, for an alloy with ke＜1, if -1≤L≤1, the interface composition C(η) increases continuously from CS to CL, and the interface is defined as inert; if L＜-1, C(η) possesses a minimum value at η=(1+L)/2L, and the interface is defined as repulsive (i.e. a “repulsive force ” occurs between the solute atoms and the interface); and if L＞1, C(η) possesses a maximum value at η=(1+L)/2L, and the interface is defined as adsorptive (i.e. an “attractive force ” occurs between the solute atoms and the interface). For an alloy with ke＞1, however, the repulsive and adsorptive interfaces become prevalent for L＞1 and L＜-1, respectively. As for the non- equilibrium behaviour of interface, a detailed discussion is presented elsewhere[24].
3 Model application
The present model was used to describe the solidification of Si-9%As (molar fraction) alloys. Fig.1 shows different model predictions, where the solid line is calculated with DL=1.5×10-9 m2/s[16], DS=3×10-13 m2/s[16], ke=0.3[4], δ=4.6×10-9 m and L=0.5, within which δ and L are the fitting parameters. The predication of the phase-field model[16] with the parameter determining the thickness of the interfacial zone ε=3.5×10-9 m, is shown as dashed line, while the predictions using Aziz’s model with VDI=0.68 m/s and using Sobolev’s model with VDI=0.68 m/s and VD=2.6 m/s are respectively imposed as the dotted line and the dashed-dotted line. Obviously, Aziz’s model fits well the experiment data only at low and moderate velocities, i.e. V＜1 m/s, Sobolev’s model fits well the experiment data covering throughout the interface velocity range. Regarding the current model predictions, the steeper profile from the present model is relatively better than that from the phase-filed model, in agreement with the experimentally measured partition coefficient for V=2 m/s. At low and moderate velocities, both model predictions almost coincide. Analogous to Aziz’s model, an asymptotic convergence of the non-equilibrium
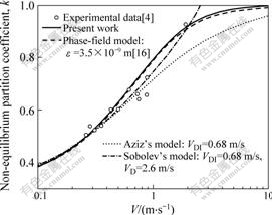
Fig.1 Partition coefficient k as function of interface velocity V for Si-9%As alloys
partition coefficient to one as V→∞ can be also described using the present model, whereas a sharp transition to k=1 at V=VD=2.6 m/s is predicted using Sobolev’s model (Fig.1). Compared with the phase field model[16], the current solute trapping model also incorporates the diffusive interface, but shows a relatively simple analytical expression.
4 Conclusions
1) By incorporating the diffusive interface into the solute drag treatment, a solute trapping model, with a simple analytical expression, is obtained.
2) When applying a basic approach defining the free energy density of the phase-field model, an interface shape function is introduced to derive the current model.
3) Both the standard chemical potential and the solute concentration change continuously across the interface, while the interface diffusion function holds continuously from the interface to the bulk liquid.
4) When applying the current model to Si-9%As (molar fraction) alloy with L=0.5, a good prediction of the steeper profile for high interface velocity, which is analogous to the phase-field model predictions of DANILOV and NESLTER, has been obtained.
References
[1] BAKER J C, CAHN J W. Solute trapping by rapid solidification [J]. Acta Metallurgica, 1969, 17: 575-578.
[2] HILLERT M. Solute drag, solute trapping and diffusional dissipation of Gibbs energy [J]. Acta Materialia, 1999, 47: 4481-4505.
[3] AZIZ M J, TSAO J Y, THOMPSON M O, PEERCY P S, WHITE C W. Solute trapping: Comparison of theory with experiment [J]. Physical Review Letters, 1986, 56: 2489-2492.
[4] KITTL J A, AZIZ M J, BRUNCO D P, THOMPSON M O. Nonequilibrium portioning during rapid solidification [J]. Journal of Crystal Growth, 1995, 148: 172-182.
[5] BRUNCO D P, THOMPSON M O, HOGLUND D E, AZIZ M J, GOSSMANN H J. Germanium partitioning in silicon during rapid solidification [J]. Journal of Applied Physics, 1995, 78: 1575-1582.
[6] KITTL J A, SANDERS P G, AZIZ M J, BRUNCO D P, THOMPSON M O. Complete experimental test of kinetic models for rapid alloy solidification [J]. Acta Materialia, 2000, 48: 4797-4811.
[7] WOOD R F. model for nonequilibrium segregation during pulsed laser annealing [J]. Applied Physics Letters, 1980, 37: 302-304.
[8] AZIZ M J. Model for solute redistribution during rapid solidification [J]. Journal of Applied Physics, 1982, 53: 1158-1168.
[9] AZIZ M J, KAPLAN T. Continuous growth model for interface motion during alloy solidification [J]. Acta Metallurgica, 1988, 36: 2335-2347.
[10] SOBOLEV S L. Rapid solidification under local nonequilibrium condition [J]. Physical Review E, 1997, 55: 6845-6854.
[11] JACKSON K A, BEATTY K M, GUDGEL K A. An analytical model for non-equilibrium segregation during crystallization [J]. Journal of Crystal Growth, 2004, 271: 481-494.
[12] GALENKO P. Solute trapping and diffusionless solidification in a binary system [J]. Physical Review E, 2007, 56: 031606.
[13] WHEELER A A, BOETTINGER W J, MCFADDEN G B. Phase-field model of solute trapping during solidification [J]. Physical Review E, 1993, 47: 1893-1909.
[14] AHMAD N A, WHEELER A A, BOETTINGER W J, MCFADDEN G B. Solute trapping and solute drag in a phase-field model for rapid solidification [J]. Physical Review E, 1998, 58: 3436-3450.
[15] KIM S G, KIM W T, SUZUKI T. Phase-field model for binary alloys [J]. Physical Review E, 1999, 60: 7186-7197.
[16] DANILOV D, NESTLER B. Phase-field modelling of solute trapping during rapid solidification [J]. Acta Materialia, 2006, 54: 4659-4664.
[17] BAKER J C. Interfacial partitioning during solidification [D]. Cambridge: Massachusetts Institute of Technology, 1970: 81-102.
[18] CAHN J W. The impurity-drag effect in grain boundary motion [J]. Acta Metallurgica, 1962, 10: 789-798.
[19] HILLERT M, SUNDMAN B. A treatment of the solute drag on moving grain boundaries and phase interfaces in binary alloys [J]. Acta Metallurgica, 1976, 24: 731-743.
[20] HILLERT M, SUNDMAN B. A solute-drag treatment of the transition from diffusion-controlled to diffusionless solidification [J]. Acta Metallurgica, 1977, 25: 11-18.
[21] ODQVIST J, SUNDMAN B, ?GREN J. A general method for calculating deviation from local equilibrium at phase interfaces [J]. Acta Materialia, 2003, 51: 1035-1043.
[22] SVOBODA J, FISCHER F D, GAMSJAGER E. Influence of solute segregation and drag on properties of migrating interfaces [J]. Acta Materialia, 2002, 50: 967-977.
[23] HILLERT M, SCHWIND M, SELLEBY M. Trapping of vacancies by rapid solidification [J]. Acta Materialia, 2002, 50: 3283-3291.
[24] WANG Hai-feng, LIU Feng, YANG Wei, CHEN Zheng, YANG Gen-cang, ZHOU Yao-he. Solute trapping model incorporating diffusive interface [J]. Acta Materialia, 2008, 56: 746-753.
(Edited by YANG Bing)
Foundation item: Projects(50501020, 50395103, 50431030) supported by the National Natural Science Foundation of China; Project(NCET-05-870) supported by Program for New Century Excellent Talents in University of China; Project(CX200706) supported by the Doctorate Foundation of Northwestern Polytechnical University, China
Corresponding author: LIU Feng; Tel: +86-29-88460374; E-mail: liufeng@nwpu.edu.cn
DOI: 10.1016/S1003-6326(09)60229-6
