J. Cent. South Univ. Technol. (2011) 18: 530-535
DOI: 10.1007/s11771-011-0727-1
Influence of pore water pressure on upper bound analysis of collapse shape for square tunnel in Hoek-Brown media
HUANG Fu(黄阜), ZHANG Dao-bing(张道兵), SUN Zhi-bin(孙志彬), WU Ben(吴贲)
School of Civil Engineering, Central South University, Changsha 410075, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract:
To investigate the effective shape of collapsing block in square tunnel subjected to pore water pressure, the analytical solution of detaching curve was derived using upper bound theorem of limit analysis with Hoek-Brown failure criterion. The work rate of pore water pressure, which was regarded as an external rate of work, was taken into account in the framework of limit analysis. Taking advantages of variational calculation, the objective function with respect to detaching curve was optimized to obtain the effective shape of collapsing block for square tunnel. According to the numerical results, it is found that the varying pore water pressure coefficient only affects the height and width of the collapsing block, whereas the shape of collapsing block remains unchanged.
Key words:
upper bound theorem; square tunnel; pore water pressure; variational calculation; Hoek-Brown media；
1 Introduction
Though the shape of most highway and railway tunnels are circular and multi-circular, the square tunnels are still widely used in underground cavities, subway stations, especially in deep-buried mine tunnels. Different from the circular tunnel, the mechanical characteristics of square tunnel are worse, due to the lack of arch structure in the roof of tunnel. Even worse, the appearance of stress concentration at the juncture of roof and tunnel wall in the square tunnel will cause the collapse of rock block over the tunnel roof. So, how to keep the cavity roof from collapsing has been a problem which has puzzled many researchers when the square tunnel is excavated in deep strata. Limit analysis, a method to bracket the actual solution in a certain range by using upper and lower bound theorems, is proved to be an effective method for analyzing the stability problems of bearing capacity of foundations [1], the earth pressures on retaining walls [2] and the stability factors of slopes [3]. As quantities of stability problems in geotechnical engineering are solved successfully by this method, some authors attempted to estimate the lower and upper bound stability solutions of tunnel in the framework of limit analysis theory [4-5]. Applying upper and lower bound theorems, the undrained stability of a shallow square tunnel under conditions of plane-strain loading is analyzed by ASSADI and SLOAN [6]. In order to obtain the upper and lower solutions of stability number, ASSADI and SLOAN [6] employed a linear programming to optimize the objective function. In a similar way, SLOAN and ASSADI [7] studied the undrained stability of a shallow square tunnel in a soil with strength increasing linearly with the depth.
With the increase of tunnel depth, the deformation process of surrounding rock becomes more and more complex, so some factors, such as pore water pressure, which have great influence on the stability of tunnel, should be taken into account. For the purpose of estimating the effect of pore water pressure on the stability analysis of slope, DAWSON et al [8] compared the stability number of slope by taking into account of pore water pressure with the solution without considering the effect of pore water pressure, and concluded that the stability number decreased with the increase of pore water pressure coefficient. Thus, the effect of pore water pressure should be included in the stability analysis for variability of geotechnical engineering using the limit analysis theory. According to the upper bound theorem of limit analysis, MICHALOWSKI [9] calculated the stability factor of slope with the effect of pore water pressure considered, and found that the influence of pore water pressure is manifested by a reduction in stability factor with an increase in pore water pressure coefficient.
The study of collapsing block of tunnel subjected to pore water pressure in saturated media is a necessary part of the design processes for tunnels excavated in deep stratum. However, the stability analysis of tunnel considering the effect of pore water pressure by limit analysis theory was rare. In the present work, taking into account of the pore water pressure, the upper bound theorem of limit analysis was applied to derive the analytical solution of shape for the collapsing block in square tunnel using the Hoek-Brown failure criterion. The study of FRALDI and GUARRACINO [10] does not take into account of the effect of pore water pressure, so the effective shape of the collapsing block in dry material is extended to the saturated rock mass.
2 Original Hoek-Brown failure criterion
In order to determine the strength of hard rock mass, Hoek and Brown proposed an empirical formula which is expressed in terms of the major and minor principal stresses. Due to its simplicity and practicability, this failure criterion is widely used in various fields of geotechnical engineering [11-15]. Different from the Mohr-Coulomb failure criterion, the Hoek-Brown criterion represented by major and minor principal stresses cannot reflect the relationship between normal and shear stresses. Therefore, the normal and shear stresses are applied to describe the shear failure of geomaterial by some researchers [16-23]. In general, the Hoek-Brown failure criterion can be written as
(1)
where σn is the normal stress, τ is the shear stress, A and B are material constants, and σci and σtm are the uniaxial compressive strength and the tensile strength of the rock mass, respectively.
3 Upper bound limit analysis with pore water pressure
As assumed by DAWSON et al [8], pore water pressure is a part of the overburden stress, increasing with the variation of depth below the ground surface, which is given by
z (2)
where 
is the unit weight of the rock mass, ru is the pore water pressure coefficient, and z is the vertical distance between the roof of the tunnel and the top of the collapsing block.
According to this assumption, pore water pressure is regarded as an external force acting on the soil skeleton. As a result, by assuming that the work of water pressure is equal to the sum of pore pressure work on skeleton and the work of the water pressure on boundary, VIRATJANDR and MICHALOWSKI [24] achieved the effects of pore water pressure in the framework of the upper bound theorem of limit analysis for slope stability, which can be written as
(3)
where 
is the strain rate in the kinematically admissible velocity field, V is the volume of the mechanism, vi is the velocity along the velocity discontinuity surface, ni is the unit component, and s is the boundary of velocity field.
From the upper bound theorem, it is stated that when the velocity boundary condition is satisfied, the load derived by equating the external rate of work to the rate of the energy dissipation in any kinematically admissible velocity field is no less than the actual collapsing load. Consequently, the upper bound theorem with the consideration of pore pressure can be expressed as
(4)
where σij is the stress component, Ti is a surcharge load on boundary, and X is the body force.
4 Upper solution of shape for collapsing block in square tunnel
As most square tunnels are buried deeply, the influence of the excavation on the rock mass is restricted in a certain region, which means that the effect of excavation beyond this region can be ignored, that is, the stress in the region far from the tunnel face maintains its original state. Due to the redistribution of stress field, the rock mass over the roof of the tunnel forms a ‘collapsing arch’ which bears a large portion of the overburden gravity. As a result, the rock mass pressure of retaining structure is far less than the stress caused by the total overburden gravity of tunnel rock mass. As illustrated in Fig.1, a kinematically admissible failure mechanism using arched detaching curve, f(x), to describe the velocity discontinuity surface is constructed.
Fig.1 Collapsing pattern of rock mass for square tunnel [10]
Based on the upper bound theorem of limit analysis, FRALDI and GUARRACINO [10] calculated the energy dissipation rate which is determined by the normal and shear stresses on the detaching surface:
(5)
where 
and 
are normal and shear plastic strain rates, respectively; 
is the first derivative of f(x), and t is the thickness of the detaching surface.
The work rate of collapsing block produced by weight is given by
(6)
where L is the half width of the collapsing block. Since the block is bounded by the velocity discontinuity line and boundary surface is assumed as a rigid material, the strain rate in the blocks can be ignored. Consequently, only the work of the water pressure on boundary s in Eq.(3) contributes to the pore water pressure effect. By substituting Eq.(2) into Eq.(3), the pore water pressure induced work rate along the detaching surface becomes
(7)
Taking into account of the effect of pore water pressure, the difference of the total energy dissipation rate and the total work rate done by external forces is
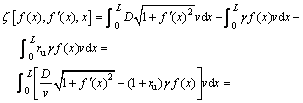
(8)
where 
is a functional which is expressed in terms of f(x) and :
(9)
According to the upper bound theorem, the load determined by the virtual work equation is not less than the actual load for any kinematically admissible velocity field. As a result, the actual shape of collapsing block can be obtained by minimizing the difference of the total energy dissipation rate and the rate of external work. To search the actual shape of collapsing block, the variational calculation is introduced to calculate the the extremum of 
. Based on the stationary value principle, extremum of is calculated by equating the variational equation to 0, which is written as
(10)
By substituting Eq.(9) into Eq.(10), a second order differential equation is found. To derive the analytical expression of the detaching curve 
the differential equation is solved and the result is
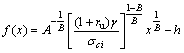(11)
where h is the integration constant.
Substituting Eq.(11) into Eq.(9), the explicit form of the functional 
can be expressed as
(12)
Substituting Eq.(9) into Eq.(8), and integrating the result, the expression of ζ is given by
(13)
where L is the half width of the collapsing block. According to the geometric significance in Fig.1, it can be found that f(x=L)=0, so Eq.(11) becomes
(16)
In order to determine the values of L and h, another equation is derived by equating the external rate of work to the rate of the energy dissipation:
(17)
Thus, the analytical expression of the detaching surface is obtained by combining Eq.(16) and Eq.(17), which is written as
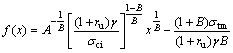(18)
5 Numerical result of collapsing shape for square tunnel
For the purpose of studying the influence of different rock parameters and pore water pressure coefficients on the shape of collapsing block for square tunnel, the height of collapsing block is plotted as a function of the collapsing block width for varied parameters, as seen in Fig.2. Compared with the results of FRALDI and GUARRACINO [10], the collapsing blocks subjected to pore water pressure is drawn in reference to different values of the parameters A, B, σtm, and γ, respectively, when the other parameters are fixed. It is observed that, both the height and the width of collapsing block are greatly affected by the variation of rock parameters when the effect of pore water pressure is not taken into account, and the changing regularity is concluded by FRALDI and GUARRACINO [10]. In the case of ru=0, the influence of pore water pressure is not taken into account in the stability analysis and the shape of collapsing block is in complete accord with the result of FRALDI and GUARRACINO [10], which means that the method of calculating pore water pressure used in this work is valid. In addition, when the pore water pressure coefficient varies from 0 to 0.25, both the height and the width of collapsing block decrease while the shape of collapsing block remains unchanged.
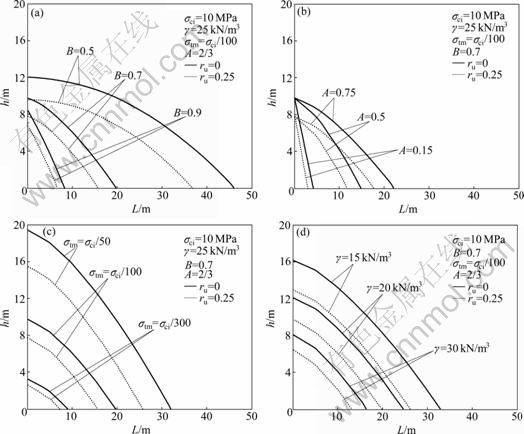
Fig.2 Shapes of collapsing blocks of square tunnel for different rock parameters and pore water pressure coefficients: (a) Shape of collapsing blocks for different B; (b) Shape of collapsing blocks for different A; (c) Shape of collapsing blocks for different σtm; (d) Shape of collapsing blocks for different γ
Furthermore, the Hoek-Brown failure criterion reduces to the Mohr-Coulomb linear criterion when the parameter B=1, which means that the shape of collapsing block in this case is no longer a parabolic curve, but a straight line. To investigate the changing regularity of collapsing mechanism under the effect of pore water pressure considered in the frame work of linear failure criterion, the shapes of collapsing blocks for rock parameter B=1 with pore water pressure coefficient varying from 0 to 0.75 are illustrated in Fig.3. Similarly, it is found that the height and width of collapsing blocks decrease with the increase of pore water pressure coefficient while the shapes of collapsing blocks do not change.
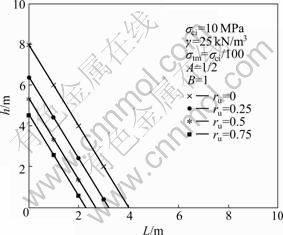
Fig.3 Shapes of collapsing blocks of square tunnel for different pore water pressure coefficients when B=1
Because the shape of collapsing block is determined by the value of rock parameter, B, it is important to study the influence of different values of B on the collapsing block subjected to pore water pressure. Thus, the collapsing blocks of rock parameters B varying from 0.5 to 0.9 are illustrated in Fig.4, while the pore water pressure coefficient ru is equal to 0.25 or 0.5. As shown in Fig.4, both the height and the width of collapsing block decrease with the increase of B with considering the effect of pore water pressure, which is the same as the changing regularity for the condition without considering pore pressure. By comparing the collapsing blocks of ru=0.25 with those of ru=0.5, it can be found that only the height and width of collapsing block decrease with the increase of pore water pressure coefficient.
Fig.4 Shapes of collapsing blocks of square tunnel for varied B and different pore water pressure coefficients: (a) ru=0.25; (b) ru=0.5
5 Conclusions
1) The upper bound theorem of limit analysis is used to derive the shape of collapsing block over the roof of square tunnel excavated in the media subjected to the Hoek-Brown failure criterion. To analyze the effect of pore water pressure on the collapsing block, the pore water pressure is included in the limit analysis by regarding it as a an external force acting on the soil skeleton. According to upper bound theorem, the objective function with respect to detaching curve is obtained, and the effective shape of collapsing block is optimized with the help of variational calculation. By introducing the effect of pore water pressure into the upper bound theorem of limit analysis, the shape of collapsing block in completely dry material is extended to saturated rock mass.
2) To evaluate the validity of the method presented, the solutions for the condition that no effect of pore water pressure is taken into account, are compared with the previous work. The good agreement shows that the method of calculating the upper solution for the shape of collapsing block subjected to pore water pressure is valid.
3) The pore water pressure coefficient has great influence on the collapsing shape of rock mass in the square tunnel. With the increase of pore water pressure coefficient, the height and width of collapsing block decrease, whereas the shape of collapsing block does not change.
4) The shape of collapsing block in the square tunnel subjected to the pore water pressure in conjunction with the Mohr-Coulomb failure criterion is obtained when the rock parameter B is equal to 1. Similar to the changing regularity concluded in nonlinear failure criterion, the height and width of collapsing block decrease while the shape of collapsing block remains unchanged.
References
[1] MERIFIELD R S, LYAMIN A V, SLOAN S W. Limit analysis solutions for the bearing capacity of rock masses using the generalised Hoek-Brown criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(6): 920-937.
[2] YANG Xiao-li, YIN Jian-hua. Estimation of seismic passive earth pressures with nonlinear failure criterion [J]. Engineering Structures, 2006, 28(3): 342-348.
[3] YANG Xiao-li, ZOU Jin-feng. Stability factors for rock slopes subjected to pore water pressure based on the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(7): 1146-1152.
[4] DAVIS E H, DUNN M J, MAIR R J, SENEVIRATNE H N. The stability of shallow tunnels and underground openings in cohesive material [J]. Geotechnique, 1980, 30(4): 397-416.
[5] LECA E, DORMIEUX L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material [J]. Geotechnique, 1990, 40(4): 581-606.
[6] ASSADI A, SLOAN S W. Undrained stability of shallow square tunnel [J]. Journal of Geotechnical Engineering ASCE, 1991, 117(8): 1152-1173.
[7] SLOAN S W, ASSADI A. Undrained stability of a square tunnel in a soil whose strength increases linearly with depth [J]. Computers and Geothehnics, 1991, 12(4): 321-346.
[8] DAWSON E M, ROTH W H, DRESCHER A. Slope stability analysis by strength reduction [J]. Geotechnique, 1999, 49(6): 835-840.
[9] MICHALOWSKI R L. Slope stability analysis: A kinematical approach [J]. Geotechnique, 1995, 45(2): 283-293.
[10] FRALDI M, GUARRACINO F. Limit analysis of collapse mechanisms in cavities and tunnels according to the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(4): 665-673.
[11] MERIFIELD R S, LYAMIN A V, SLOAN S W. Limit analysis solutions for the bearing capacity of rock masses using the generalised Hoek-Brown criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(6): 920-937.
[12] CARRANZA-TORRES C, FAIRHURST C. The elasto-plastic response of underground excavations in rock masses that satisfy the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(6): 777-809.
[13] LI A J, MERIFIELD R S, LYAMIN A V. Stability charts for rock slopes based on the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(5): 689-700.
[14] JIMENEZ R, SERRANO A, OLALLA C. Linearization of the Hoek and Brown rock failure criterion for tunnelling in elasto-plastic rock masses [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(7): 1153-1163.
[15] YANG Xiao-li. Seismic displacement of rock slopes with nonlinear Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 948-953.
[16] FRALDI M, GUARRACINO F. Analytical solutions for collapse mechanisms in tunnels with arbitrary cross sections [J]. International Journal of Solids and Structures, 2010, 47(2): 216-223.
[17] YANG X L. Seismic bearing capacity of a strip footing on rock slopes [J]. Canadian Geotechnical Journal, 2009, 46(8): 943-954.
[18] HOEK E, BROWN E T. Practical estimate the rock mass strength [J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(8): 1165-1186.
[19] YANG X L, YIN J H. Slope stability analysis with nonlinear failure criterion [J]. Journal of Engineering Mechanics, 2004, 130(3): 267- 273.
[20] YANG X L, YIN J H. Slope equivalent Mohr-Coulomb strength parameters for rock masses satisfying the Hoek-Brown criterion [J]. Rock Mechanics and Rock Engineering, 2010, 43(4): 505-511.
[21] YANG X L, YIN J H. Linear Mohr-Coulomb strength parameters from the nonlinear Hoek-Brown rock masses [J]. International Journal of Non-linear Mechanics, 2006, 41(8): 1000-1005.
[22] RAFAEL J, ALCIBIADES S, CLAUDIO O. Linearization of the Hoek and Brown rock failure criterion for tunneling in elasto-plastic rock masses [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(7): 1153-1163.
[23] HOEK E, BROWN E T. Practical estimate the rock mass strength [J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(8): 1165-1186.
[24] VIRATJANDR C, MICHALOWSKI R L. Limit analysis of submerged slopes subjected to water drawdown [J]. Canadian Geotechnical Journal, 2006, 43(8): 802-814.
(Edited by YANG Bing)
Foundation item: Project(09JJ1008) supported by Hunan Provincial Science Foundation, China; Project(CX2009B043) supported by Hunan Provincial Postgraduate Innovation Program, China
Received date: 2010-01-21; Accepted date: 2010-04-26
Corresponding author: HUANG Fu, PhD; Tel: +86-731-82656248; E-mail: hfzndx2002@yahoo.com.cn
