- Abstract:
- 1 Introduction▲
- 2 System description...▲
- 3 Results and discus...▲
- 4 Conclusions▲
- References
- Figure
- Figure 1 Organic Rankine cycle represented in temperature-entropy (T–s) diagrams:
- Figure 2 Comparison of Tc (a) and Pc (b) calculated by NIST and GCM
- Figure 3 Comparisons of r (a) and c (b) calculated by NIST and GCM
- Figure 4 Comparison of c/r calculated by NIST and GCM
- Figure 5 Comparisons of wout (a) and η (b) calculated by NIST and GCM

ARTICLE
J. Cent. South Univ. (2019) 26: 2234-2243
DOI: https://doi.org/10.1007/s11771-019-4169-5
Evaluation of working fluids for organic Rankine cycles using group-contribution methods and second-law-based models
MA Wei-wu(马卫武)1, WANG Lin(王琳)1, LIU Tao(刘韬)2, LI Min(李旻)1
1. School of Energy Science and Engineering, Central South University, Changsha 410083, China;
2. Changsha Institute of Mining Research, Changsha 410083, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract:
The group-contribution (GC) methods suffer from a limitation concerning to the prediction of process-related indexes, e.g., thermal efficiency. Recently developed analytical models for thermal efficiency of organic Rankine cycles (ORCs) provide a possibility of overcoming the limitation of the GC methods because these models formulate thermal efficiency as functions of key thermal properties. Using these analytical relations together with GC methods, more than 60 organic fluids are screened for medium-low temperature ORCs. The results indicate that the GC methods can estimate thermal properties with acceptable accuracy (mean relative errors are 4.45%-11.50%); the precision, however, is low because the relative errors can vary from less than 0.1% to 45.0%. By contrast, the GC-based estimation of thermal efficiency has better accuracy and precision. The relative errors in thermal efficiency have an arithmetic mean of about 2.9% and fall within the range of 0-24.0%. These findings suggest that the analytical equations provide not only a direct way of estimating thermal efficiency but an accurate and precise approach to evaluating working fluids and guiding computer-aided molecular design of new fluids for ORCs using GC methods.
Key words:
Cite this article as:
MA Wei-wu, WANG Lin, LIU Tao, LI Min. Evaluation of working fluids for organic Rankine cycles using group-contribution methods and second-law-based models [J]. Journal of Central South University, 2019, 26(8): 2234-2243.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-019-4169-51 Introduction
Organic Rankine cycles (ORCs) have recently attracted considerable interest because of the urgent need for generating power from low-grade heat sources [1-3]. Low-grade heat sources (e.g., solar heat, geothermal energy, and industry waste heat) differ from high-temperature heat sources in temperature and energy density, with a difference that makes the Rankine cycle use steam inefficient [4-6]. Rankine cycles using organic working fluids (i.e., ORCs) tend to be more appropriate for converting low-grade heat into power [2]. A key aspect of applying ORCs is the selection of an appropriate organic working fluid. In this context, an appropriate organic fluid means that the working fluid is safe, environmentally friendly, and thermodynamically efficient. It is, however, a great challenge to achieve the optimum selection of organic fluids for Rankine cycles because of the diversity of organic fluids, performance criteria, and heat-source characteristics [7-9].
Many studies have been devoted to evaluating and selecting organic fluids for the Rankine cycle [5, 8, 10-28]. Roughly speaking, these studies can be divided into two groups: the first group has used experimentally validated equations of state (EoS) or property diagrams (e.g., NIST reference database [29]) to evaluate organic fluids [5, 8, 10]. The previous studies have examined the influence of organic fluids on net power output [30, 31], turbine expansion ratio [32, 33], thermal efficiency [34-36], exergetic efficiency [37-39], minimum superheat degree [40-42], and component sizes [43]. Among these indexes, the greatest interest is the correlations between thermal efficiency of ORCs and critical temperature [44, 45], normal boiling point [46], molecular complexity [47-50], Jacob number [35, 46, 51], figure of merit [46], molar mass [52, 53], acentric factor [54], and reduced ideal gas heat capacity [55]. But, the problem with these studies is that they require complete experimental data to create EoS for the evaluated fluids and thus can only screen a limited list of organic fluids.
By contrast, the second group of the studies employed group-contribution (GC) methods to calculate thermal properties of organic working fluids [11-22, 24-28]. The GC methods are often used in computer-aided molecular design (CAMD) of new fluids for ORCs because they can predict physical and thermal properties without recourse to complete experimental data [14, 15, 18, 19]. HUKKERIKAR et al [21] presented revised and improved GC models for 18 pure components properties. They also analyzed the uncertainties in the estimated property values. A robust method was presented for assessing utilization efficiency (Second Law Efficiency) of ORCs plants based on molecular group contribution methods in Ref. [24]. BROWN et al [12, 13] combined P-R EoS and GC methods to evaluate the performance properties for well-described and not-so-well- described working fluids in ORC. They only compared these physical properties of working fluids for ORCs. These thermal parameters were not systematically compared with the NIST database, in which these parameters are important for the evaluation of working fluids in ORCs. MARTIN et al [18] and WHITE et al [19] proposed an optimization framework by combining GC methods, SAFT-γ Mie EoS with an ORC power system to select working fluids based on hydrocarbon function groups. LAMPE et al [25, 27] provided an approach to select working fluids and optimize the process for ORCs, underlying the PC-SAFT EoS in a continuous-molecular targeting approach (CoMT- CAMD). Unlike LAMPE et al thought that the ORC system is tailored to the specific application, PALMA-FLORES et al [26] presented a new approach that can design novel fluids by using PC-SAFT with GC methods. But these studies in Ref. [25-27] are limited in a low-temperature heat source for ORC system. A methodology was developed to estimate the process-related properties of the generated working fluids for ORCs based on GC methods and Peng-Robinson (P-R) EoS in Refs. [14, 15, 28]. However, the above models, in which the required properties are calculated by combining EoS with GC methods, are able to produce iterative calculation. The involved iterative calculation is a more complicated process and is adverse to the evaluation of working fluids’ application for ORCs. These predicted thermal properties are considered an objective parameter to select organic fluids. However, the screened fluid only determined by GC methods may not be the one that has the best thermal performance in a cycle. The thermal performance of a cycle depends, not only on GC methods, but on many other parameters (such as Ja number) for design and optimization. Therefore, it would be of interest and useful to develop a method that can predict performance indices of ORCs based on properties yielded by GC methods. Such a method can not only screen a wide range of organic fluids but predict indices relating directly to ORCs, overcoming the disadvantages of EoS.
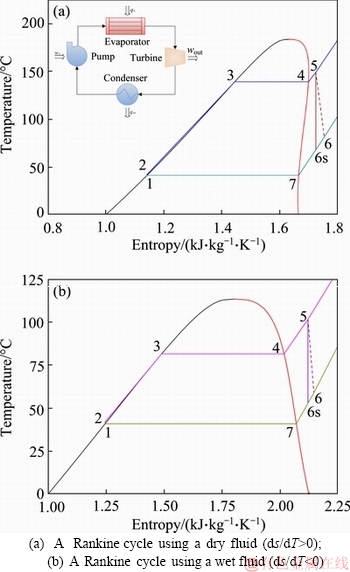
Figure 1 Organic Rankine cycle represented in temperature-entropy (T–s) diagrams:
The purpose of this paper is to report a method that evaluates the thermodynamic performance of ORCs using the thermal properties obtained from GC methods. To achieve this purpose, we develop a set of analytical solutions for work and thermal efficiency of ORCs, which is of satisfactory accuracy and enables us to calculate work and thermal efficiency using thermal properties given by GC methods. This method is validated by screening more than 60 organic fluids that are available in the NIST reference database. The comparison shows that the GC-based methods can estimate work and thermal efficiency with relative errors within 10.8% and 2.9%, smaller than those of thermal properties.
2 System description and modeling
2.1 Analytical models for ORCs
Figure 1 shows single organic Rankine cycle in T–s diagrams. As can be seen, a Rankine cycle works in subcritical conditions and requires several numbers of components, which includes isentropic compression in a pump, constant pressure heat addition in an evaporator, isentropic expansion in a turbine, and constant pressure heat rejection in a condenser. The working fluid is isentropically compressed in the pump (1-2) and flows into the heat exchangers to take the available energy from the heat source (2-5). Then the highest temperature of the fluid is reduced in the turbine to produce mechanical power, which is transformed into electricity through a generator (5-6s). To close the loop, the fluid is condensed and pumped again (6s-1). Conventionally, the work and thermal efficiencies of an ORC are calculated by enthalpies of state points (Figure 1), a method that requires high-accuracy EoS or property diagrams. A major problem with GC methods is that they cannot yield enthalpies and thus work and thermal efficiency. To overcome this problem, we developed several analytical equations for work and thermal efficiency that are functions of operating temperatures and several thermal properties of the working fluid. These explicit equations can extend the prediction ability of GC methods, without recourse to EoS.
These analytical equations can be derived from a rigorous entropy-generation analysis of ORCs and have been published elsewhere [56]. Thus only final expressions are summarized here. For the ORC shown in Figure 1, the thermal efficiency can be determined by Eq. (1):
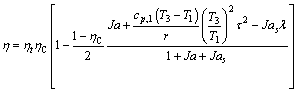 (1)
(1)
where
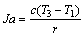 (2)
(2)
 (3)
(3)
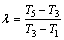 (4)
(4)
 (5)
(5)
where r is the latent heat of evaporation of the working fluid at the evaporating temperature T3; c, cp, cp,1 are the average heat capacity during the preheating process 2-3, the superheating process 4-5 and the desuperheating process 6s-7, respectively; ηC denotes the Carnot efficiency: ηC=(T3-T1)/T3; 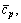
 are the averages of cp, r, and volumetric expansion coefficient of saturate-vapor from T1 to T3, which can be well approximated by the values at (T1+T3)/2.
are the averages of cp, r, and volumetric expansion coefficient of saturate-vapor from T1 to T3, which can be well approximated by the values at (T1+T3)/2.
Equation (1) is very general but somewhat complicated; it is desirable to simplify Eq. (1) according to the feature of working fluids. Organic fluids fall into three categories: dry, wet, and isentropic fluids in terms of the slope of the saturated vapor curve in the T-s plane (Figure 1). If a dry fluid is used in medium-low temperature ORCs, superheating 4-5 may be unnecessary or insignificant. In this case, Eq. (1) reduces to follows:
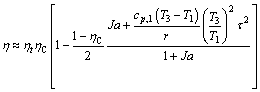 (6)
(6)
For wet fluids, desuperheating 6s-7 is generally unnecessary (Figure 1(b)), and Eq. (1) becomes
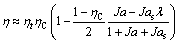 (7)
(7)
For isentropic fluids, the entropy generation of desuperheating 6s-7 is usually offset by the superheating 4-5. Therefore, Eq. (1) reduces to the following extremely simple form:
 (8)
(8)
The work produced by the turbine is the difference in vapor enthalpy between inlet and outlet states, and can be approximated by Eq. (9):
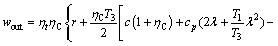
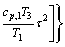 (9)
(9)
2.2 Group-contribution methods
A GC method is a computational model which estimates physical and thermodynamic properties of pure components by summarizing the contributions of simple groups that form the molecules [21]. Once the contribution of a functional group is determined, it remains unchanged and is transferable between different molecules. GC methods can quickly estimate properties with few computational resources [22]; thus, they are the most widely used property prediction method. Various GC models have been developed for estimating thermodynamic properties. The following summarizes the models used in this work.
The GC+ models proposed by HUKKERIKAR et al [21] were used for estimating critical temperature Tc, critical pressure Pc, and acentric factor ω.
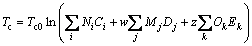 (10)
(10)
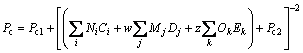 (11)
(11)
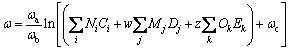 (12)
(12)
where Tc0, Pc1, Pc2, ωa, ωb, ωc are values of the universal constants for the properties: Tc0= 181.6738 K,Pc1=0.0519 bar, Pc2-0.5=0.1155 bar-0.5, and ωa=0.9132, ωb=0.447, ωc=1.0039; Ni, Mj, Ok denote the number of i, j, k groups in the molecule; Ci, Dj, Ek are group-contribution values for the considered group.
The GC model for the enthalpy of vaporization is a function of the reduced temperature Tr [57]:
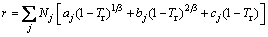 (13)
(13)
where the reduced temperature Tr is defined as T/Tc; Nj denotes the number of j group in the molecule; aj, bj, cj are group-contribution values for the considered group; the unit of r is kJ/mol.
The used GC model for the ideal gas heat capacity is [58]:


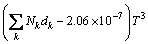 (14)
(14)
where Nk denotes the number of k group in the molecule; ak, bk, ck, dk are group-contribution values for the considered group.
The liquid heat capacity, related to the ideal gas capacity at the same temperature, can be estimated by the following expression [59]:
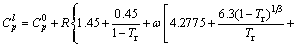
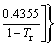 (15)
(15)
where Tr denotes reduced temperature, Tr=T/Tc; R is gas constant. All the group-contribution values occurring in these models can be found in the literature, thus they are not repeated here.
3 Results and discussion
More than 60 organic fluids are screened as candidates for ORCs, including dry, wet, and isentropic fluids. Before examining the performance of ORCs, we compared the thermodynamic properties calculated by the GCMs and those calculated by the NIST reference database [29], because we found research has not yet systematically validated GC methods in the ORCs field (including the refrigeration field). In Figures 2-5, the two gray lines represent the relative errors of -10% and 10%, respectively.
3.1 Tc and Pc
Figure 2 compares critical temperature and pressure (Tc and Pc) calculated by the GC methods (GCM) and the NIST database for the selected working fluids. The comparison shows that the agreement of Tc is slightly better than Pc. Compared to NIST, the predictions of Tc by the GC methods have an average relative error smaller than 5.0% and those of Pc have an average relative error smaller than 10.0%. Among the screened fluids, only 9 working fluids have relative errors in Tc exceeding 10.0%, but 20 fluids have relative errors in Pc exceeding 10.0% (Figure 2). The maximum relative errors in Tc and Pc are slightly larger than 30.0% and 40.0%,respectively.
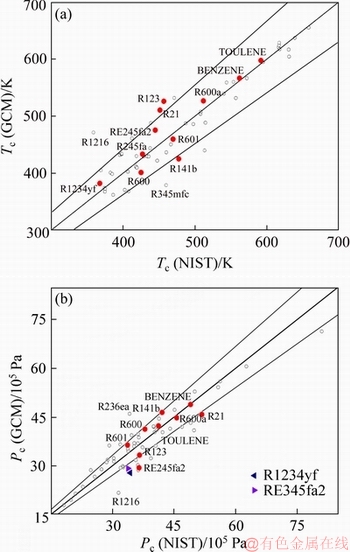
Figure 2 Comparison of Tc (a) and Pc (b) calculated by NIST and GCM
3.2 r and c
The latent heat of evaporation r and the heat capacity of the saturated liquid c are most relevant to the evaluation of working fluids for ORCs. It is generally desirable to use in ORCs an organic fluid having a relatively large r and small average c [3, 43, 53]. For a given T1 and T3, Figure 3 compares r and c calculated by the NIST database and the GC methods. Again, Figure 3 shows a contrast between r and c: the average errors of the prediction of r and c are 5.85% and 11.5%, respectively; and only 11 organic fluids have relative errors in r larger than 10.0%, but 30 fluids have relative errors in c exceeding 10.0%. Unlike Tc, Pc and r, c given by the GC methods tends to be smaller than that given by the NIST data, implying that the GC models for c may involve systematic bias in c (Figure 3).

Figure 3 Comparisons of r (a) and c (b) calculated by NIST and GCM
The systematic bias of c contributes accordingly to the systematic bias in c/r (Figure 4). The average relative errors in c/r fall within a range of 0.75%-55.6% with an average error about 12.0%. The quantity c/r contains key thermodynamic information of a working fluid [60, 61] and may be the most important parameter for screening working fluids. In conjunction with T1 and T3, c/r has been used to define the dimensionless variable Ja number.
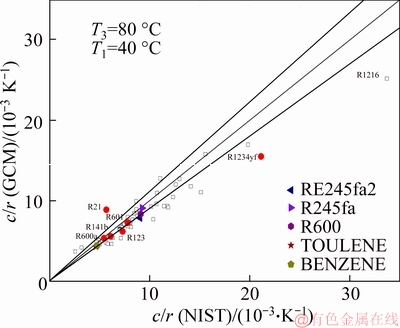
Figure 4 Comparison of c/r calculated by NIST and GCM
Therefore, the estimate of c/r is even more important than the estimates of other properties. From the preliminary study, it can be concluded that while the relative error is slightly larger than those of c and r, the estimate of c/r from the GC method is still acceptable for most organic fluids.
3.3 wout and η
The problem with the GC methods is that they can only predict physical and thermodynamic properties of working fluids and fail to predict the thermodynamic performances of ORCs, such as work and thermal efficiency, because the GC methods cannot estimate enthalpy. The present authors have developed a set of explicit equations for these two performance indexes by a rigorous entropy-generation analysis of ORCs [56]. These equations express the work and thermal efficiency as analytical functions of evaporating and condensing temperatures, as well as key thermal properties (not the state variable enthalpy). Having these equations, we can determine wout and η directly using the properties estimated by the GC methods (referred to as GC-based method hereafter).
Figure 5 compares the work wout and the thermal efficiency η estimated by the GC-based method with those given by the NIST database (enthalpies were calculated first). As shown in Figure 5(a), wout given by the GC-based method tends to be greater than the counterpart yielded by the NIST database, namely, there is a systematic bias in the prediction of wout. The relative error of wout is within the range of 0.18%-33.9%, and the average error is slightly larger than 10.0%. But, the accuracy and precision of the estimation of η are surprisingly high (Figure 5(b)). For the given T1 and T3, the GC-based approach yields thermal efficiency with an average relative error of 3.0%. Among the screened fluids, the prediction for R227ea has the maximum relative error (≈24.0%), and only 3 organic fluids have relative errors exceeding 10.0%. Some reasons for these fluids with larger relative errors are as follows: on one hand, the analytical expressions for the thermal efficiency of ORCs yield relative error; on the other hand, these parameters (such as Tc, Pc, r and c) evaluated by GC methods have different errors for different compounds, especially for sample or symmetrical compounds such as R21 (Ja≈40%) or R227ea (η≈24%).
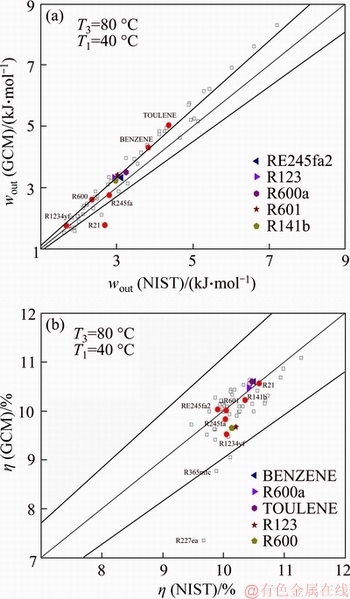
Figure 5 Comparisons of wout (a) and η (b) calculated by NIST and GCM
The high accuracy and precision of the prediction of η can greatly facilitate the application of GC methods in computer-aided molecular design (CAMD). The GC methods are particularly useful in CAMD because they can predict physical properties of pure components with high computational efficiency [18, 27]. Generally, the CAMD identifies an optimum molecular structure for an ORC using some physical or thermal properties as performance measures [14, 15]. As shown above, although the GC methods can estimate thermal properties for most organic fluids with an acceptable accuracy (<10-15%), these estimated properties should be used with caution because the maximum relative error can be as large as 30%-40%. The wide variability in the property estimation, without a doubt, may lead to non-optimal molecular design from the property- based optimization. From this viewpoint, using the estimated η as the objective function can reduce the uncertainty in CAMD because of the high accuracy and precision of the estimation of η.
Moreover, compared with the use of fluid properties, it should be more appropriate to use η as the performance measures in CAMD. On one hand, thermal efficiency is the direct measure of the thermodynamic performance of ORCs, which depends on many properties instead of one (see Eq. (1)). On the other hand, using η can greatly simplify the optimum problem involved in CAMD. First, it can simplify the objective function. In a conventional CAMD, various properties are included in the objective function used in a multi-objective optimization problem, e.g., heat capacity, vaporization enthalpy, etc. Second, since the thermal efficiency can be determined directly from the estimated properties, this approach can further simplify the process-related simulation of ORCs, which is necessary in a CAMD.
4 Conclusions
This paper suggests a set of analytical expressions for the thermal efficiency of ORCs. These analytical expressions, together with GC models for thermal properties, can greatly facilitate the screen and evaluation of working fluids for ORCs. Using the GC methods, several key thermal properties (including Tc, Pc, r and c) can be predicted for more than 60 organic fluids. The screen work reveals that the used GC methods can yield acceptable accuracy for these properties; the average relative errors fall within the range of 4.45%-11.50%. But the precision of the prediction is somewhat low because the variability in the relative errors can be large (from less than 0.1% to 45.0%).
By contrast, the prediction of thermal efficiency has better accuracy and precision than those of thermal properties. The average relative error in η is about 2.9% compared with those given by the NIST database, and the variability of the errors is within the range of 0-24.0%. In fact, only the predictions of 3 fluids have relative errors in η exceeding 10.0%. Based on the results, we inferred that direct estimation of thermal efficiency using the properties given by the GC methods appears to be a reliable approach to evaluating working fluids and guiding computer-aided molecular design of new fluids for ORCs.
References
[1] YANG M H, YEH R H. Thermodynamic and economic performances optimization of an organic Rankine cycle system utilizing exhaust gas of a large marine diesel engine [J]. Applied Energy, 2015, 149: 1-12. DOI: 10.1016/ j.apenergy.2015.03.083.
[2] TCHANCHE B F, LAMBRINOS G, FRANGOUDAKIS A, PAPADAKIS G. Low-grade heat conversion into power using organic Rankine cycles-A review of various applications [J]. Renewable and Sustainable Energy Reviews, 2011, 15: 3963-3979. DOI: 10.1016/j.rser.2011.07.024.
[3] CHEN H, GOSWAMI D Y, STEFANAKOS E K. A review of thermodynamic cycles and working fluids for the conversion of low-grade heat [J]. Renewable and Sustainable Energy Reviews, 2010, 14: 3059-3067. DOI: 10.1016/ j.rser.2010.07.006.
[4] SHU Ge-qun, LIU Li-na, TIAN Hua, WEI Hai-qiao, YU Guo-peng. Parametric and working fluid analysis of a dual-loop organic Rankine cycle (DORC) used in engine waste heat recovery [J]. Applied Energy, 2014, 113: 1188-1198. DOI: 10.1016/j.apenergy.2013.08.027.
[5] SALEH B, KOGLBAUER G, WENDLAND M, FISCHER J. Working fluids for low-temperature organic Rankine cycles [J]. Energy, 2007, 32: 1210-1221. DOI: 10.1016/ j.energy.2006.07.001.
[6] QUOILIN S, DECLAYE S, TCHANCHE B F, LEMORT V. Thermo-economic optimization of waste heat recovery Organic Rankine Cycles [J]. Applied Thermal Engineering, 2011, 31: 2885-2893. DOI: 10.1016/j.applthermaleng. 2011.05.014.
[7] TOFFOLO A, LAZZARETTO A, MANENTE G, PACI M. A multi-criteria approach for the optimal selection of working fluid and design parameters in organic Rankine cycle systems [J]. Applied Energy, 2014, 121: 219-232. DOI: 10.1016/j.apenergy.2014.01.089.
[8] MIKIELEWICZ D, MIKIELEWICZ J. A thermodynamic criterion for selection of working fluid for subcritical and supercritical domestic micro CHP [J]. Applied Thermal Engineering, 2010, 30: 2357-2362. DOI: 10.1016/ j.applthermaleng.2010.05.035.
[9] SARKAR J. Property-based selection criteria of low GWP working fluids for organic Rankine cycle [J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2017, 39: 1419-1428. DOI: 10.1007/s40430-016-0605-8.
[10] LAI N A, WENDLAND M, FISCHER J. Working fluids for high-temperature organic Rankine cycles [J]. Energy, 2011, 36: 199-211. DOI: 10.1016/j.energy.2006.07.001.
[11] BARBIERI E S, MORINI M, PINELLI M. Development of a model for the simulation of organic Rankine cycles based on group contribution techniques [C]// ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition. 2011, 3: 1011-1019. DOI: 10.1115/GT2011-45616.
[12] BROWN J S, BRIGNOLI R, DAUBMAN S. Methodology for estimating thermodynamic parameters and performance of working fluids for organic Rankine cycles [J]. Energy, 2014, 73: 818-828. DOI: 10.1016/j.energy.2014.06.088.
[13] BRIGNOLI R, BROWN J S. Organic Rankine cycle model for well-described and not-so-well-described working fluids [J]. Energy, 2015, 86: 93-104. DOI: 10.1016/j.energy.2015. 03.119.
[14] PAPADOPOULOS A I, STIJEPOVIC M, LINKE P. On the systematic design and selection of optimal working fluids for organic Rankine cycles [J]. Applied Thermal Engineering, 2010, 30: 760-769. DOI: 10.1016/j.applthermaleng.2009. 12.006.
[15] PAPADOPOULOS A I, STIJEPOVIC M, LINKE P, SEFERLIS P, VOUTETAKIS S. Power generation from low enthalpy geothermal fields by design and selection of efficient working fluids for organic rankine cycles [J]. Chemical Engineering Transactions, 2010, 21: 61-66. DOI: 10.3303/CET10210011.
[16] SU Wen, LI Zhao, DENG Shuai. Developing a performance evaluation model of organic Rankine cycle for working fluids based on the group contribution method [J]. Energy Conversion and Management, 2017, 132: 307-315. DOI: 10.1016/j.enconman.2016.11.040.
[17] SU Wen, LI Zhao, DENG Shuai. Simultaneous working fluids design and cycle optimization for organic Rankine cycle using group contribution model [J]. Applied Energy, 2017, 202: 618-627. DOI: 10.1016/j.apenergy.2017.03.133.
[18] MARTIN T, WHITE O A, ANDREW J. HASLAM, CHRISTOS N, MARKIDES C N. Industrial waste-heat recovery through integrated computer-aided working-fluid and ORC system optimization using SAFT-γ Mie [J]. Energy Conversion and Management, 2017, 150: 851-869. DOI: 10.1016/j.enconman.2017.03.048.
[19] WHITE M T, OYEWUNMI O A, CHATZOPOULOU M A, PANTALEO A M, HASLAM A J, MARKIDES C N. Computer-aided working-fluid design, thermodynamic optimization and thermos-economic assessment of ORC systems for waste-heat recovery [J]. Energy, 2018, 161: 1181-1198. DOI: 10.1016/j.energy.2018.07.098.
[20] OYEWUNMI O A, TALEB A I, HASLAM A J, MARKIDES C N. On the use of SAFT-VR Mie for assessing large-glide fluorocarbon working-fluid mixtures in organic Rankine cycles [J]. Applied Energy, 2016, 163: 263-282. DOI: 10.1016/j.apenergy.2015.10.040.
[21] HUKKERIKAR A S, SARUP B, KATE A T, ABILDSKOV J, SIN G, GANI R. Group-contribution+(GC+) based estimation of properties of pure components: Improved property estimation and uncertainty analysis [J]. Fluid Phase Equilibria, 2012, 321: 25-43. DOI: 10.1016/j.fluid. 2012.02.010.
[22] SU Wen, ZHAO Li, DENG Shuai. Group contribution methods in thermodynamic cycles: Physical properties estimation of pure working fluids [J]. Renewable and Sustainable Energy Reviews, 2017, 79: 984-1001. DOI: 10.1016/j.rser.2017.05.164.
[23] SCHILLING J, LAMPE M, GROSS J, BARDOW A. 1-stage CoMT-CAMD: An approach for integrated design of ORC process and working fluid using PC-SAFT [J]. Chemical Engineering Science, 2017, 159: 217-230. DOI: 10.1016/j.ces.2016.04.048.
[24] LUKAWSKI M Z, DIPIPPO R, TESTER J W. Molecular property methods for assessing efficiency of organic Rankine cycles [J]. Energy, 2018, 142: 108-120. DOI: 0.1016/ j.energy.2017.09.140.
[25] LAMPE M, STAVROU M, SCHILLING J, SAUER E, GROSS J, BARDOW A. Computer-aided molecular design in the continuous-molecular targeting framework using group-contribution PC-SAFT [J]. Computers & Chemical Engineering, 2015, 81: 278-287. DOI: 10.1016/ j.compchemeng.2015.04.008.
[26] PALMA-FLORES O, FLORES-TLACUAHUAC A, CANSECO-MELCHOR G. Optimal molecular design of working fluids for sustainable low-temperature energy recovery [J]. Computers & Chemical Engineering, 2015, 72: 334-349. DOI: 10.1016/j.compchemeng.2014.04.009.
[27] LAMPE M, STAVROU M, BUCKER HM, GROSS J, BARDOW A. Simultaneous optimization of working fluid and process for organic rankine cycles using PC-SAFT [J]. Industrial & Engineering Chemistry Research, 2014, 53: 8821-8830. DOI: 10.1021/ie5006542.
[28] PAPADOPOULOS A I, STIJEPOVIC M, LINKE P, SEFERLIS P, VOUTETAKIS S. Toward optimum working fluid mixtures for organic rankine cycles using molecular design and sensitivity analysis [J]. Industrial & Engineering Chemistry Research, 2013, 52: 12116-12133. DOI: 10.1021/ie400968j.
[29] LEMMON E W, MCLINDEN M O. NIST standard reference database 23, NIST reference fluid thermodynamic and transport properties—REFPROP, version 9.1 [M]. Gaithersburg: National Institute of Standards and Technology, 2013.
[30] HEBERLE F, BRUGGEMANN D. Exergy based fluid selection for a geothermal organic Rankine cycle for combined heat and power generation [J]. Applied Thermal Engineering, 2010, 30: 1326-1332. DOI: 10.1016/ j.applthermaleng.2010.02.012.
[31] REIS M M L, GALLO W L R. Study of waste heat recovery potential and optimization of the power production by an organic Rankine cycle in an FPSO unit [J]. Energy Conversion and Management, 2018, 157: 409-422. DOI: 10.1016/j.enconman.2017.12.015.
[32] RAHBAR K, MAHMOUD S, ADADAH R K,MOAZAMI N. Modelling and optimization of organic Rankine cycle based on a small-scale radial inflow turbine [J]. Energy Conversion and Management, 2015, 91: 186-198. DOI: 10.1016/j.enconman.2014.12.003.
[33] KANG S H. Design and experimental study of ORC (organic Rankine cycle) and radial turbine using R245fa working fluid [J]. Energy, 2012, 41: 514-524. DOI: 10.1016/ j.energy.2012.02.035.
[34] DELGADO-TORRES A M, GARCIA-RODRIGUEZ L. Analysis and optimization of the low-temperature solar organic Rankine cycle (ORC) [J]. Energy Conversion and Management, 2010, 51: 2846-2856. DOI: 10.1016/ j.enconman.2010.06.022.
[35] WANG Dong-xiang, LING Xiang, PENG Hao, LIU Lin, TAO Lan-lan. Efficiency and optimal performance evaluation of organic Rankine cycle for low grade waste heat power generation [J]. Energy, 2013, 50: 343-352. DOI: 10.1016/j.energy.2012.11.010.
[36] BRAIMAKIS K, PREIβINGER M, BRUGGEMANN D, KARELLAS S, PANOPOULOS K. Low grade waste heat recovery with subcritical and supercritical organic Rankine cycle based on natural refrigerants and their binary mixtures [J]. Energy, 2015, 88: 80-92. DOI: 10.1016/j.energy.2015. 03.092.
[37] YU Guo-peng, SHU Ge-qun, TIAN Hua, WEI Hai-qiao, LIU Li-na. Simulation and thermodynamic analysis of a bottoming organic rankine cycle (ORC) of diesel engine (DE) [J]. Energy, 2013, 51: 281-290. DOI: 10.1016/j.energy. 2012.10.054.
[38] SHU Ge-qun, LI Xiao-ning, TIAN Hua, LIANG Xing-yu, WEI Hai-qiao, WANG X. Alkanes as working fluids for high-temperature exhaust heat recovery of diesel engine using organic Rankine cycle [J]. Applied Energy, 2014, 119: 204-217. DOI: 10.1016/j.apenergy.2013.12.056.
[39] AHMADI P, DINCER I, ROSEN M A. Exergo- environmental analysis of an integrated organic Rankine cycle for trigeneration [J]. Energy Conversion and Management, 2012, 64: 447-453. DOI: 10.1016/j.enconman. 2012.06.001.
[40] YANG Kai, ZHANG Hong-guang, SONG Song-song, YANG Fu-bin, LIU Hao, ZHAO Gung-yao, ZHANG Jian, YAO Bao-feng. Effects of degree of superheat on the running performance of an organic Rankine cycle (ORC) waste heat recovery system for diesel engines under various operating conditions [J]. Energies, 2014, 7: 2123-2145. DOI: 10.3390/en7042123.
[41] ROY J P, MISHRA M K, MISRA A. Performance analysis of an organic Rankine cycle with superheating under different heat source temperature conditions [J]. Applied Energy, 2011, 88: 2995-3004. DOI: 10.1016/j.apenergy.2011.02.042.
[42] ZHOU Nai-jun, WANG Xiao-yuan, CHEN Zhuo, WANG Zhi-qi. Experimental study on organic Rankine cycle for waste heat recovery from low-temperature flue gas [J]. Energy, 2013, 55: 216-225. DOI: 10.1016/j.energy. 2013.03.047.
[43] BAO Jun-jiang, ZHAO Li. A review of working fluid and expander selections for organic Rankine cycle [J]. Renewable and Sustainable Energy Reviews, 2013, 24: 325-342. DOI: 10.1016/j.rser.2013.03.040.
[44] LIU B T, CHIEN K H, WANG C C. Effect of working fluids on organic Rankine cycle for waste heat recovery [J]. Energy, 2004, 29: 1207-1217. DOI: 10.1016/j.energy.2004.01.004.
[45] XU Jin-liang, YU Chao. Critical temperature criterion for selection of working fluids for subcritical pressure organic Rankine cycles [J]. Energy, 2014, 74: 719-733. DOI: 10.1016/j.energy.2014.07.038.
[46] KUO C R, HSU S W, CHANG K H, WANG C C. Analysis of a 50 kW organic Rankine cycle system [J]. Energy, 2011, 36: 5877-5885. DOI: 10.1016/j.energy.2011.08.035.
[47] RAYEGAN R, TAO Y X. A procedure to select working fluids for solar organic rankine cycles (ORCs) [J]. Renewable Energy, 2011, 36: 659-670. DOI: 10.1016/ j.renene.2010.07.010.
[48] BRASZ J, HOLDMANN G. Power production from a moderate-temperature geothermal resource [J]. Transactions- Geothermal Resources Council, 2005, 29: 729-733. DOI: 10.1016/j.esd.2011.06.002.
[49] INVERNIZZI C, IORA P, SILVA P. Bottoming micro- Rankine cycles for micro-gas turbines [J]. Applied Thermal Engineering, 2007, 27: 100-110. DOI: 10.1016/ j.applthermaleng.2006.05.003.
[50] HUNG T C. Waste heat recovery of organic Rankine cycle using dry fluids [J]. Energy Conversion and Management, 2001, 42: 539-553. DOI: 10.1016/S0196-8904(00)00081-9.
[51] HE Chao, LIU Chao, ZHOU Meng-tong, XIE Hui, XU Xiao-xiao, WU Shuang-ying, LI You-rong. A new selection principle of working fluids for subcritical organic Rankine cycle coupling with different heat sources [J]. Energy, 2014, 68: 283-291. DOI: 10.1016/j.energy.2014.02.050.
[52] JUNG D, PARK S, MIN K. Selection of appropriate working fluids for Rankine cycles used for recovery of heat from exhaust gases of ICE in heavy-duty series hybrid electric vehicles [J]. Applied Thermal Engineering, 2015, 81: 338-345. DOI: 10.1016/j.applthermaleng.2015.02.002.
[53] STIJEPOVIC M Z, LINKE P, PAPADOPOULOS A I, GRUJIC A S. On the role of working fluid properties in organic Rankine cycle performance [J]. Applied Thermal Engineering, 2012, 36: 406-413. DOI: 10.1016/ j.applthermaleng.2011.10.057.
[54] DRESCHER U, BRUGGEMANN D. Fluid selection for the organic Rankine cycle (ORC) in biomass power and heat plants [J]. Applied Thermal Engineering, 2007, 27: 223-228. DOI: 10.1016/j.applthermaleng.2006.04.024.
[55] LUKAWSKI M Z, TESTER J W, DIPIPPO R. Impact of molecular structure of working fluids on performance of organic Rankine cycles (ORCs) [J]. Sustainable Energy & Fuels, 2017, 1: 1098-1111. DOI: 10.1039/C6SE00064A.
[56] MA Wei-wu, LIU Tao, MIN Rui, LI Min. Effects of physical and chemical properties of working fluids on thermodynamic performances of medium-low temperature organic Rankine cycles (ORCs) [J]. Energy Conversion and Management, 2018, 171: 742-749. DOI: 10.1016/j.enconman.2018.06.032.
[57] TU C H, LIU C P. Group-contribution estimation of the enthalpy of vaporization of organic compounds [J]. Fluid Phase Equilibria, 1996, 121: 45-65. DOI: 10.1016/ 0378-3812(96)03008-7.
[58] JOBACK K G, REID R C. Estimation of pure-component properties from group-contributions [J]. Chemical Engineering Communications, 2007, 57: 233-243. DOI: 10.1080/00986448708960487.
[59] POLING B E, PRAUSNITZ J M, O’CONNELL J P. The properties of gas and liquids [J]. Journal of the American Chemical Society, 2001, 123(27): 6745-6745. DOI: 10.1021/ja0048634.
[60] LI Min, ZHAO Bing-xiong. Analytical thermal efficiency of medium-low temperature organic Rankine cycles derived from entropy-generation analysis [J]. Energy, 2016, 106: 121-130. DOI: 10.1016/j.energy.2016.03.054.
[61] MA Wei-wu, FANG Song, SU Bo, XUE Xin-pei, LI Min. Second-law-based analysis of vapor-compression refrigeration cycles: Analytical equations for COP and new insights into features of refrigerants [J]. Energy Conversion and Management, 2017, 138: 426-434. DOI: 10.1016/ j.enconman.2017.02.017.
(Edited by YANG Hua)
中文导读
基于基团贡献法和热力学第二定律模型对有机朗肯循环(ORCs)工质的评估
摘要:基团贡献(GC)法一般用于预测有机物的热力学属性参数,但对过程指标的预测能力有限,如热力循环过程的效率。本文发展了一种结合GC法和有机朗肯循环(ORC)热效率解析模型的方法,可以高效快速地估算有机朗肯循环的热效率,从而在某种程度上克服GC方法的局限性。利用GC法与ORC热效率解析模型,筛选了60多种用于中低温有机朗肯循环的有机工质。首先,运用GC方法预测了60多种有机工质的临界温度Tc,临界压力Pc,潜热r,液体的定压比热容c等热力学属性。其次,基于由热力学第二定律推得的ORC解析模型,可直接由GC法预测的热力学参数直接确定ORC的输出功wout和热效率η等性能指标。计算结果表明,与NIST数据相比,本文采用的GC模型具有足够的精度来估算热力学参数(Tc,Pc,r,c,wout,η的平均相对误差分别为4.45%,9.29%,5.85%,11.5%,10.8%,2.9%)。其中热效率的平均相对误差最小(约为2.9%),且所有预测值的误差在0~24%的范围内。本研究表明GC方法与ORC解析模型结合,不仅提供了一种估算热效率的直接方法(无需状态方程),并且提供了一种快速准确的方法来评估有机工质的热力学性能。本文研究成果也为指导基于GC法的ORC有机工质计算机辅助设计提供借鉴。
关键词:有机朗肯循环;基团贡献法;工质;属性估算;计算机辅助设计
Foundation item: Project (51778626) supported by the National Natural Science Foundation of China
Received date: 2019-05-30; Accepted date: 2019-07-17
Corresponding author: LI Min, PhD, Professor; Tel: +86-18573119955; E-mail: cnlimin78@gmail.com; ORCID: 0000-0003-0029-585X
Abstract: The group-contribution (GC) methods suffer from a limitation concerning to the prediction of process-related indexes, e.g., thermal efficiency. Recently developed analytical models for thermal efficiency of organic Rankine cycles (ORCs) provide a possibility of overcoming the limitation of the GC methods because these models formulate thermal efficiency as functions of key thermal properties. Using these analytical relations together with GC methods, more than 60 organic fluids are screened for medium-low temperature ORCs. The results indicate that the GC methods can estimate thermal properties with acceptable accuracy (mean relative errors are 4.45%-11.50%); the precision, however, is low because the relative errors can vary from less than 0.1% to 45.0%. By contrast, the GC-based estimation of thermal efficiency has better accuracy and precision. The relative errors in thermal efficiency have an arithmetic mean of about 2.9% and fall within the range of 0-24.0%. These findings suggest that the analytical equations provide not only a direct way of estimating thermal efficiency but an accurate and precise approach to evaluating working fluids and guiding computer-aided molecular design of new fluids for ORCs using GC methods.
- Evaluation of working fluids for organic Rankine cycles using group-contribution methods and second-law-based models


