J. Cent. South Univ. Technol. (2011) 18: 1677-1684

DOI: 10.1007/s11771-011-0888-y

Combined effect of steel fibres and steel rebars on impact resistance of high performance concrete

CHEN Xiang-yu(陈相宇)^{1, 2}, DING Yi-ning(丁一宁)², C. Azevedo³

1. Shanghai Bekaert Ergang Co., Ltd, Shanghai 200131, China;

2. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116023, China;

2. Centre of Mathematics, University of Minho, Braga 4700, Portugal

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Key words:

impact resistance; high performance concrete; fibre; Weibull distribution；

1 Introduction

The development of modern building engineering and infrastructure reveals a strong demand on high performance engineering materials including high strength, high toughness and energy absorption ability, etc. High performance concrete (HPC), which makes remarkable advances during recent years, plays an important role in the field of structure engineering.

Resistance to impact load is recognized today as one of the important properties of HPC used for structural applications [1]. It is well known that the addition of steel fibres to HPC can strongly modify its mechanical properties, improving both the tensile and flexural strengths, as well as pronouncedly increasing post-cracking ductility and amending fatigue performance [2-7]. In addition to the improvements mentioned, steel fibre reinforcement has remarkably positive effect on the impact resistance of concrete to dynamic forces such as the impulsive loads for pile driving and pile column, or dynamic loads from earthquakes and ocean waves. Although the influence of fibre on the impact resistance of concrete has been investigated [1-2, 7-14], the focus is on the plain concrete or on the fibres reinforced effect only. At present, the most building structures and infrastructures are made of steel reinforced concrete. However, the study on the hybrid effect of steel fibres and steel rebars on the impact resistance of HPC is very limited.

Some impact test methods have been suggested by different guidelines [7,13]. They may be used for investigation of the impact resistance of concrete, such as explosive test, drop-weight test, and projectile impact test. Among them, the drop-weight test method [7] recommended by the ACI Committee 544, is regarded as the simplest one and has been used widely in the study on the impact resistance of concrete. In this experiment, the numbers of blows to first visible crack (N₁) as well as to final failure (N₂) were recorded. Thereafter, both of them were used to evaluate the impact resistance and to demonstrate the improved performance of SFRC with and without steel rebar compared with normal concrete. However, experimental data obtained from the ACI impact test could be noticeably scattered as reported in the previous studies. The sources of large scatter in results may be attributed to the following reasons [2, 8-10]:

1) The subjectivity of the test is due to the visual identification of the first crack, which may occur in any direction [9].

2) The impact resistance of concrete is based on a single point of impact, which might happen to be on a hard particle of coarse aggregate, or on a soft area of mortar, or on the different types of fibre.

3) Concrete is not a homogeneous material. The variation of mix design may cause the change in impact resistance, including aggregate type and shape, geometry of the fibre, fibres distribution, etc.

4) The height of the drop hammer is difficult to control exactly due to the handmade process.

5) The free falling of the drop weight can be influenced by the initial hand actuated work, so the experimental result can be influenced by the man-made factors.

In the view of features of impact experimental results, statistical analysis technique should be the best choice for clarifying the test results and enhancement effects of steel fibres on concrete.

The purpose of this study is, therefore, experimentally to investigate the effect of steel fibres and steel rebars on improving the impact resistance of normal concrete and subsequently to propose a realistic evaluation method for the test results. It will be helpful to extend the use of SFRC and further clarify the nature of impact behavior of HPC.

2 Experimental

2.1 Materials

In this test program, the mix design of concrete was as follows: cement CEM I 52.5R, fly ash 106 kg/m?, aggregate 38% 0-4 mm and 62% 5-10 mm, superplasticizer (SP) 1.1% of binder, and water binder ratio 0.34. In order to study the effect of steel fibres and steel rebars on the impact resistance, the hooked-end Dramix steel fibres and Ф12 steel rebars were added into the concrete (see Fig.1). Table 1 presents the dimensions and physical properties of the steel fibre.

Six groups of samples were tested based on different fibre dosages and steel rebar contents in the concrete. The mixture proportions of various test groups used in this work are given in Table 2.

The dosage of 20 kg/m? and 35 kg/m? steel fibre has some negative influence on the workability of fresh SFRC. The addition of 1.1% SP can maintain a relatively good workability for all types of concrete. In the present test, the slump-flows of NC, SFRC20 and SFRC35 were 60, 58 and 55 cm, respectively.

2.2 Testing methods

Because the impact resistance of SFRC was strongly influenced by the fabrication process and the distribution of fibres [2], in this study, the uniform distribution of fibres was ensured so that balling of fibres can be avoided. First, the coarse and fine aggregates were mixed for 3 min, and then the cement and fly ash were added. All the solid materials were mixed for     2 min, and during this procedure, about 50% (volume fraction) of water was added. Next, the fibres were fed continuously for a few minutes and then the remaining water together with SP was added slowly. The whole mixing operation took about 8 min. The concrete specimens were cast in cylindrical moulds of 152 mm in diameter and 75 mm in thickness and compacted using a vibrating table. After casting, the specimens were covered with plastic sheets. All specimens were demoulded after 24 h, and then stored in a concrete curing room at (20±3) °C and relative humidity over 90%. Six disc specimens were prepared for each mix proportion, so a total of 36 samples were prepared.

In order to decrease the variations of impact results, a new drop-weight test device based on the recommendation of ACI Committee 544 was fabricated, as shown in Fig.2. With the help of positioning magnetic switch, the concrete specimens were impacted at the same point by the freely falling drop hammer so that the boundary conditions of each impact were kept evenly in this test.

Fig.1 Hooked-end steel fibres and Ф12 steel rebar

Table 1 Physical properties and dimensions of steel fibre

Table 2 Mix proportions

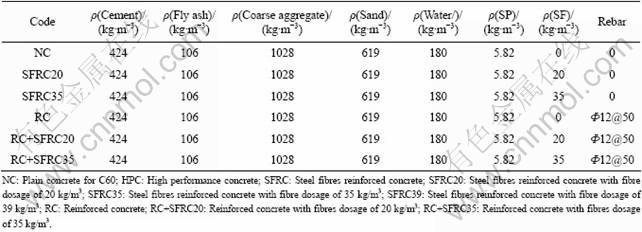
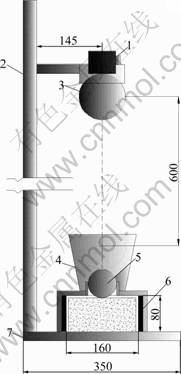
Fig.2 Schematic diagram of new drop-weight test device: 1— Positioning magnetic switch; 2—Impact frame; 3—Drop hammer; 4—Guidance; 5—Steel ball; 6—Positioning lug; 7—Base plate

The specimens of this test were referred to the precast pile tip with a reinforcement ratio of 1.9%. So, the thickness of specimens was set as (75±3) mm in order to ensure the minimum thickness of concrete cover. The impact test was performed in accordance with the impact testing procedures recommended by ACI Committee 544. The test was carried out by dropping a hammer weighing 4.5 kg from a height of 600 mm repeatedly on a 64 mm diameter hardened steel ball, which is placed on the top of the centre of the cylindrical disc, as shown in Fig.2. The number of blows to cause the first visible crack on the disc top was recorded as the first-crack resistance factor (N_l). After that, the dropping operation continued to break the cracked disc into pieces touching three of the lugs. The number of blows up to the touching action was recorded as the failure resistance factor (N₂).

3 Analysis and results

3.1 Compressive strength

The average values of compressive strength of concrete with and without fibre reinforcement after 28 d are illustrated in Table 3. The addition of fibres aids in converting the brittle concrete into a ductile material, but no significant trend of improving compressive strength is observed. The compressive strength of all the samples exceeds 60 MPa after 28 d. Therefore, the proposed mix design has produced the concrete that satisfactorily meets the strength requirement of HPC.

Table 3 Compressive strength test results (MPa)

Moreover, the compressive strength was used as a means of quality control here [15-16]. The average 28 d compressive strengths of NC, SFRC20 and SFRC35 are 67.3, 66.3 and 66.1 MPa, and the standard deviations are 2.9, 3.8 and 2.8 MPa, respectively. The corresponding coefficients of variation of NC, SFRC20 and SFRC35 are 4.4%, 5.7% and 4.3%, respectively.

The standard deviation indicates a good quality control over the production of the concrete specimens. The values of the coefficient of variation further show the evidence of sufficient quality control. The coefficient of variation of NC and SFRC35 is lower than a limit of 5% suggested by SWAMY and STAVRIDES [16] for good quality control, even though the coefficients of variation of SFRC20 is slightly higher than the limit. However, DAY [15] suggested that a coefficient of variation between 5% and 10% generally represents a reasonable quality control.

3.2 Impact resistance

The drop-weight test results of all specimens are presented in Table 4. It can be observed that the test data exhibit a large variation even if the new drop-weight test device is used. It appears that some statistical techniques would be particularly appropriate for the analysis of such test results. Therefore, in the present study, statistical analysis of the test data is carried out and the typical results are listed in Table 5.

Based on the statistical analysis in Table 5, it can be seen that in terms of the blows to the first crack (N₁) and to the final failure (N₂), the means are 189 and 210 for SFRC20. Compared with NC, the impact resistance factors of SFRC 20 increase by about 1 160% and 1 300%, respectively. For SFRC35, the impact resistance factors increase by about 1 920% and 2 613%, respectively. It can therefore be concluded that the addition of steel fibres improves the impact resistance, and with the increase of fibre content, a strong improvement in impact resistance is achieved. The improvement of the impact resistance can be mainly due to the randomly distributed fibres in the concrete matrix. These fibres, each acting as a miniature energy-absorbing mechanism, support a certain percentage of the load during each impact event, thus SFRC discs can bear more impact blows and improve the first crack impact resistance of SFRC discs over that of their non-fibre plain concrete counterparts. After the first crack occurs and is followed by the others, the fibres spanning across these cracks act not only as energy-absorbing mechanisms, but also as load transfer mechanisms [10]. The mechanisms may defend the cracked SFRC discs against the tendency to fail into different pieces, therefore improving the failure impact resistance.

The mean value of the blows to first crack of RC, RC+SFRC20 and RC+SFRC35 also have an increase by 40%-60% compared with NC. Moreover, the mean value of the blows to failure for RC, RC+SFRC20 and RC+SFRC35 are 350, 1 196 and 1 232, increased by   2 233%, 7 873% and 8 113% compared with NC, respectively. This means that the energy absorption of RC+SFRC specimens is greatly enhanced at ultimate failure due to the randomly distributed fibres in the concrete matrix and the composite action between the steel fibers and steel rebars.

3.3 Composite effect of fibres and rebars on impact resistance of concrete

The mean values of the blows to the final failure (N₂) are illustrated in Fig.3. It can be seen that N₂ values of RC, SFRC20 and RC+SFRC20 are 350, 210 and 1 196, respectively. It should be noted that compared with the sum of specimen RC and specimen SFRC20, the mean value of specimen RC+SFRC20 increases by about 113%. Similarly, compared with the sum of specimen RC and specimen SFRC35, the mean value of specimen RC+SFRC35 increases by about 63%, as shown in Fig.4. So, it can be concluded that the combination of steel fibres and steel rebars shows much greater positive hybrid effect on the impact resistance than that of the sum of concrete with mono-reinforcement.

Table 4 Drop-weight test results

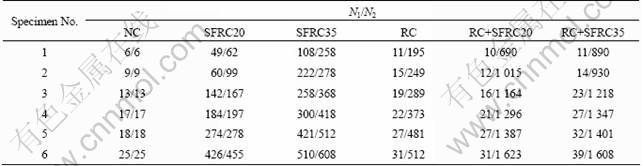
Table 5 Statistical analyses of drop-weight test results

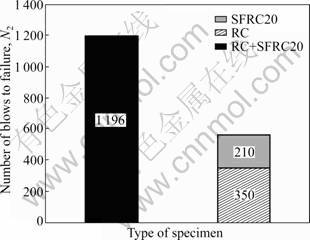
Fig.3 Comparison of N₂ values between specimen RC+ SFRC20 and sum of specimen RC and specimen SFRC20

Figure 5 illustrates the different failure patterns of specimens with different reinforcements. It can be observed that the NC discs are usually broken into two pieces and show a brittle behavior, whereas the RC, SFRC and RC+SFRC discs are normally broken into four or more pieces and show well ductile properties. This phenomenon indicates that the addition of mono- reinforcement like mono-fiber or only steel rebar allows more uniform stress distribution, and the use of the combination of steel fibre and steel rebar can provide more even stress distribution in the concrete matrix, which results in the increase of impact resistance. This means that the stress redistribution is more uniform in the samples with hybrid fiber and rebar subjected to impact than that in the samples with only steel fibres or only rebars.

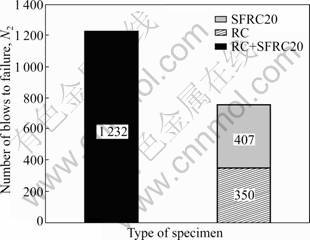
Fig.4 Comparison of N₂ values between specimen of RC+ SFRC35 and sum of specimen RC and specimen SFRC35

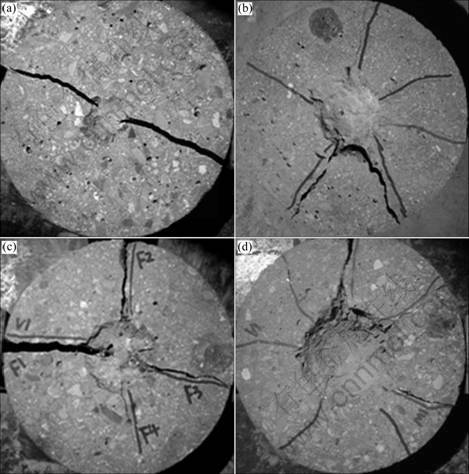
Fig.5 Comparison of failure patterns of specimens with different reinforcements: (a) NC; (b) RC; (c) SFRC; (d) RC+SFRC

3.4 Distribution of first-crack and failure resistance factor

A number of mathematical probability models are available and have been employed for the statistical description of fatigue and impact test data of concrete in the past few decades [2, 8-10, 17-19]. Although the logarithmic-normal (lognormal) distribution model is often used in this field, it should be noted that the lognormal hazard function has a unique behavior: it increases initially with the increase of time, then decreases and approaches to zero. This means that the items with a lognormal distribution have a higher chance of failing as they age for some period of time, but after survival to a specific age, the failure probability decreases as time increases. This phenomenon does not meet the physical behavior of the progressive deterioration of engineering materials under repeated dynamic loading. By contrast, the Weibull distribution has an increasing hazard function with time when the shape parameter α is larger than 1. Many investigations have proved that two-parameter Weibull distribution is more applicable to the fatigue life evaluation of concrete [17-19]. Basically, the mechanism of impact test is similar to that of the fatigue test; therefore, the two-parameter Weibull distribution is adopted and a graphical method is employed to clarify the distribution characteristic of impact resistance factor of six groups of samples.

The probability distribution function f(n) and the cumulative distribution function F_N(n) of the Weibull probability law may be expressed as

              (1)

                           (2)

where n denotes the specific values of the random variable N; α denotes the shape parameter; u denotes the scale parameter; n₀ denotes the location parameter or minimum life. n≥n₀, α>0, and u≥n₀.

The probability of survivorship function may be defined as

                                                      (3)

It is reasonable to assume that the minimum life of concrete n₀ is 0 in fatigue and impact applications. Then, Eq.(3) can be derivated to the following form:

                                                 (4)

Taking logarithms twice of both sides of Eq.(4) gives

                             (5)

Thus, Eq.(5) can be used to verify whether the statistical distribution of the impact resistance factor (N₁, N₂ ) of six groups of samples follows the two-parameter Weibull distribution. Two steps are adopted to conduct the verification. In the first step, the impact resistance data, including the numbers of blows to first crack (N₁) and to the final failure (N₂), are arranged in ascending order, and then an empirical survivorship function can be analyzed:

                                                               (6)

where i is the failure order number and k is the total number of sample for a given type of specimens. If an approximately linear relationship is observed between ln[ln(l/L_N)] and ln n, we can assume that the two- parameter Weibull distribution is a reasonable assumption for the statistical description of impact resistance factor of the six types of concrete. Subsequently, the regression coefficients about α, α ln u and correlation coefficient R² can be obtained by linear analysis, respectively.

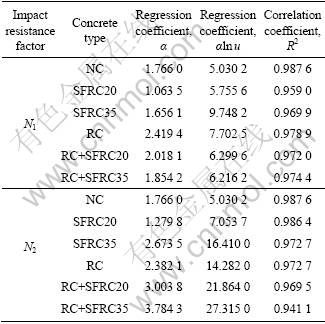
For the experimental data regarding the first crack resistance factor (N₁) of NC, SFRC20, SFRC35, RC, RC+SFRC20 and RC+SFRC35, the plots of dispersion and the respective adjusted lines are obtained in Fig.6. The same exercise has been done by using experimental data regarding the final failure resistance factor (N₂) in Fig.7, and the regression coefficients about α, α ln u and the correlation coefficient R² corresponding to six types of concrete samples are demonstrated in Table 6.

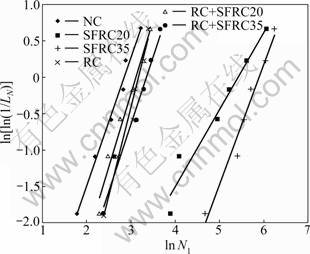
Fig.6 Linear regression of N₁ in Weibull distribution

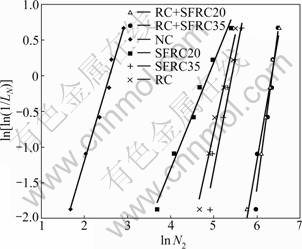
Fig.7 Linear regression of N₂ in Weibull distribution

Table 6 Linear regression coefficients of impact resistance in Weibull distribution

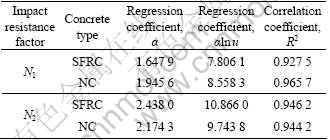
As an example, the test results of NATARAJA et al [2] for NC and SFRC with a 39 kg/m³ steel fibres are also reinvestigated numerically by using the same linear analysis and given in Table 7, and the regression coefficients of α, α ln u and the correlation coefficient R² corresponding to the test results of NATARAJA [2] are listed in Table 8.

From the above discussion, it can be seen that a linear relationship exists well between ln[ln(l/L_N)] and  ln N. This demonstrates that the two-parameter Weibull distribution is a reasonable analysis tool for the description of the blows to first crack (N₁) and to failure (N₂).

Table 7 Drop-weight test results of NATARAJA et al [2]

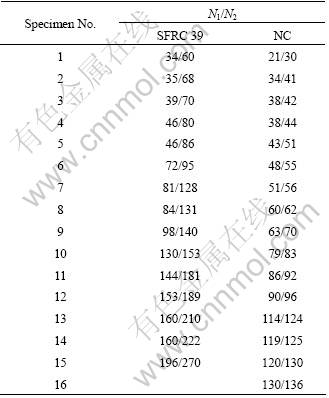
Table 8 Linear regression coefficients of impact resistance of NATARAJA et al’s results in Weibull distribution

4 Conclusions

1) The impact resistance of NC can be improved by addition of steel fibres. The impact resistance can be enhanced with the increase of fibre content.

2) The blows to final failure of RC+SFRC is much more than the sum of RC and SFRC, which indicates that the combination of steel fibre and steel rebar provides much greater positive composite effect on the improvement of impact resistance than that in the samples with only steel fibres or only rebars.

3) The blows to first crack (N₁) and to failure (N₂) of six types of concrete samples are proved to fit the two-parameter Weibull distribution well by the goodness-of-fit technique.

References

[1] ZHANG M H, LI L, Paramasivam P. Flexural toughness and impact resistance of steel-fibre-reinforced lightweight concrete [J]. Magazine of Concrete Research, 2004, 56(5): 251-262.

[2] Nataraja M, Dhang N, Gupta A. Statistical variations in impact resistance of steel fiber-reinforced concrete subjected to drop weight test [J]. Cement and Concrete Research, 1999, 29(7): 989-995.

[3] Ding Y, ZHANG Y, THOMAS A, Kusterle W. The investigation on strength and flexural toughness of fibre cocktail reinforced self-compacting high performance concrete [J]. Construction and Building Materials, 2009, 23: 448-452.

[4] Camps G, Turatsinze A, Sellier A, Escadeillas G, Bourbon X. Steel-fiber-reinforcement and hydration coupled effects on concrete tensile behavior [J]. Engineering Fracture Mechanics, 2008, 75: 5207-5216.

[5] Lu X, Hsu C. Behavior of high strength concrete with and without steel fiber reinforcement in triaxial compression [J]. Cement and Concrete Research, 2006, 36: 1679-1685.

[6] Altun F, Haktanir T, Ari K. Effects of steel fiber addition on mechanical properties of concrete and RC beams [J]. Construction and Building Materials, 2007, 21: 654-661.

[7] ACI Committee 544. Measurement of properties of fiber reinforced concrete [J]. ACI Materials Journal, 1988, 85(6): 583-593.

[8] Song P, Wu J, Hwang S, Sheu B. Assessment of statistical variations in impact resistance of high-strength steel fiber-reinforced concrete [J]. Cement and Concrete Research, 2005, 35(2): 393-399.

[9] Atef B, Ashraf F, Andrew K. Statistical variations in impact resistance of polypropylene fibre-reinforced concrete [J]. International Journal of Impact Engineering, 2006, 32: 1907-1920.

[10] Song P, Hwang S, Sheu B. Statistical evaluation for impact resistance of steel-fibre-reinforced concrete [J]. Magazine of Concrete Research, 2004, 56(8): 437-442.

[11] Wang Z, Liu Y, Shen R. Stress-strain relationship of steel fiber-reinforced concrete under dynamic compression [J]. Construction and Building Materials, 2008, 22: 811-819.

[12] Mahmoud N, Afroughsabet V. Combined effect of silica fume and steel fibers on the impact resistance and mechanical properties of concrete [J]. International Journal of Impact Engineering, 2010, 37: 879-886.

[13] Wang L, Wang H, JIA J. Impact resistance of steel-fibre- reinforced lightweight-aggregate concrete [J]. Magazine of Concrete Research, 2009, 67(7): 539-547.

[14] Mohammadi Y, Carkon A, Singh S, Kaushik S. Impact resistance of steel fibrous concrete containing fibers of mixed aspect ratio [J]. Construction and Building Materials, 2009, 23: 183-189.

[15] Day K. Concrete mix design, quality control and specification [M]. London: E&FN Spon, 1999.

[16] Swamy R, Stavrides H. Some statistical considerations of steel fibre reinforced composites [J]. Cement and Concrete Research, 1976, 6(2): 201-216.

[17] LI Hui, Zhang Mao-hua, Ou Jin-ping. Flexural fatigue performance of concrete containing nano-particles for pavement [J]. International Journal of Fatigue, 2007, 29(7): 1292-1301.

[18] Raif S, Irfan A. Statistical analysis of bending fatigue life data using Weibull distribution in glass-fiber reinforced polyester composites [J]. Materials and Design, 2008, 29(6): 1170-1181.

[19] Raman B, Rakesh C. Fatigue-life distributions and failure probability for glass-fiber reinforced polymeric composites [J]. Composites Science and Technology, 2009, 69(9): 1381-1387.

(Edited by YANG Bing)

Foundation item: Project(50578026) supported by the National Natural Science Foundation of China; Project supported by FCT (SFRH/BPD/22680/2005) and Research Center of Mathematics of the University of Minho through the FCT Pluriannual Funding Program

Received date: 2010-07-09; Accepted date: 2010-10-29

Corresponding author: DING Yi-ning, Professor, PhD; Tel: +86-13478783053; E-mail: ynding@hotmail.com