
J. Cent. South Univ. (2019) 26: 2891-2905
DOI: https://doi.org/10.1007/s11771-019-4222-4
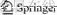
Improving behavior of semi-supported steel plate shear walls
Ali GHAMARI1, Abbas AKBARPOUR2, Ali GHANBARI3
1. Department of Civil Engineering, Darreh Shahr Branch, Islamic Azad University, Darreh Shahr, Iran;
2. School of Civil Engineering, South Tehran Branch, Islamic Azad University, Tehran, Iran;
3. Department of Structural Engineering, Aria University of Science and Sustainability, Tehran, Iran
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract:
In spite of the good performance of the steel plate shear wall (SPSW) in recent earthquakes and experimental studies, the need for huge columns to surround the infill plate is a major shortcoming of the system. This shortcoming can be resolved by using semi-supported SPSW. The semi-supported SPSW has secondary columns that prevent the transfer of stress from the infill plate to the main columns. In spite of extensive experimental and numerical investigations on SPSWs, there are many ambiguities regarding the behavior of the semi-supported SPSW. Although stress in the columns is reduced, incomplete diagonal tension field action is formed in the infill plate that creates new problems. In this paper, a new type of semi-supported SPSW is presented in which the steel plate and the secondary columns are angled. The creation of the angle of the plate and the secondary column makes it possible to use the full capacity of the steel plate as well as the capacity of the secondary columns. Numerical results showed that the wall with a 60° angle has a favorable performance relative to the semi-supported wall. Moreover, with the 60° angle, stiffness, strength and energy absorption is increased. The angle of the secondary columns has little effect on the non-elastic stiffness. Nevertheless, using a wall with an angle of more than 90° can neutralize the wall’s behavior relative to conventional walls. Therefore, the wall with a 60° angle as an optimal angle is recommended.
Key words:
steel plate shear wall (SPSW); ductility; stiffness; ultimate strength; R factor;
Cite this article as:
Ali GHAMARI, Abbas AKBARPOUR, Ali GHANBARI. Improving the behavior of semi-supported steel plate shear walls utilizing an innovative idea [J]. Journal of Central South University, 2019, 26(10): 2891-2905.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-019-4222-41 Introduction
Steel plate shear walls (SPSWs) are an effective and economical system that has shown a successful performance in past earthquakes as well as experimental studies. This system has good ductility, high lateral strength and stiffness. In addition to these advantages, it has the ability to run the opening (door and window) [1, 2]. Experimental studies [3-7] as well as numerical studies [8-12] on this system have confirmed the benefits that have persuaded designers to use the system in practical projects. In spite of the considerable advantages of SPSWs, the post-buckling behavior of the SPSW causes a large amount of stress to transfer from the infill plate to the main columns [13]. Therefore, columns with high moments of inertia are required for SPSWs. To overcome this shortcoming, some methods have been proposed to reduce the stress in the columns surrounding the infill plate: the use of horizontal struts, as shown in Figure 1(a), the use of composted walls, as shown in Figure 1(b), the use of fiber reinforced polymer (FRP) [3, 14], and the use of low yield point (LYP) steel for the steel wall [15]. Although the methods reduce stress in the main columns, they do not reduce the columns’ required moment of inertia.
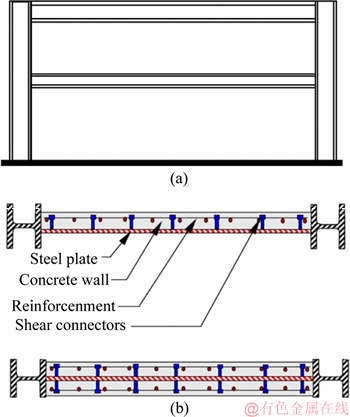
Figure 1 SPSW with horizontal strut [16] (a) and composite-SPSW [2] (b)
The semi-supported steel shear wall is one of the innovative ideas to reduce the stress transferred to the main columns. In this idea, secondary- columns are used surrounding the plate to prevent the stresses caused by the plate from being transmitted to the main columns. Since the secondary-columns are not affected by gravity load, their duty is merely to provide side support for the steel plate. The performance of this system has been numerically investigated by researchers [17, 18] as well as experimental studies [19, 20]. Figure 2 shows the distribution of the tension field action in the conventional and semi-supported steel plate shear wall. As shown in this figure, tension stress in the semi-supported wall is not transmitted to the main column, but in the conventional wall, the column is affected by the stress caused by the infill plate.
Although the stress in the main column is reduced in the semi-supported wall, due to the low moment of inertia of the secondary columns, an incomplete diagonal tension field is formed [17]. Therefore, the total capacity of the plate is not used. In this paper, a new semi-supported SPSW is presented. In this idea, the steel plate as well as the secondary columns in the semi-supported shear wall are angularly used.
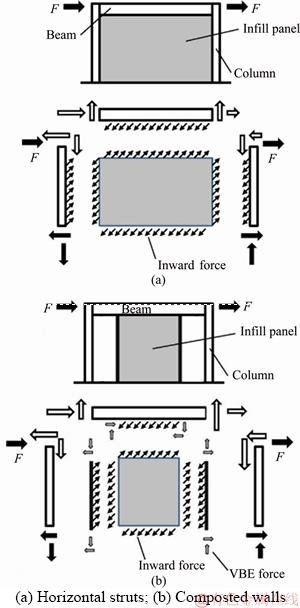
Figure 2 Stress distribution on SPSWs [13]:
2 Methodology
In the proposed semi-supported SPSW, the steel plate and the secondary-columns are angled to the horizon. Several angles of the wall is examined by finite element (FE) analysis to achieve the appropriate angle. In addition to examining the effect of the angle, the effect of the infill plate thickness of the semi-supported SPSW is evaluated and a new model is presented to estimate the pushover curve without FE modeling.
3 Pushover curve of the proposed system
Figure 3 shows a schematic of the proposed system. Since FE modeling and nonlinear analysis are complicated, it is necessary to present a simple model to calculate the load-displacement curve without FE modeling. In order to overcome this problem, a simple method is presented to calculate the load-displacement curve considering linear and nonlinear zones without FE modeling.
Figure 3 Convectional system (a) and proposed system (b) of a semi-supported steel plate shear wall
To obtain the load-displacement diagram of the angled semi-supported steel shear wall, first, load-displacement diagrams for the main frame (MF), secondary columns (SC) and plate (P) are computed separately. Then the obtained load- displacement curves are summed together. In this case the steel shear wall is considered as a separate frame (Figure 4); to obtain its load-displacement diagram with regards to the presented theory, the steel plate and the frame can be detached from each other. The above-mentioned diagram can be obtained for each of these separate entities and then by summing their effects, the overall diagram can be sketched. The effect of a crack is also considered in the present investigation, and the load- displacement diagram is modified accordingly.
A thin steel shear wall plate usually buckles under small loads, and this buckling normally occurs prior to yielding. Based on the classic theory, the elastic shear buckling stress is expressed as
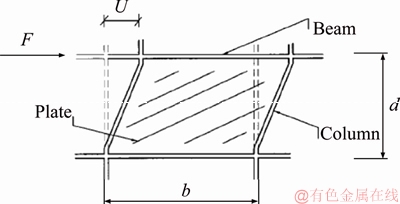
Figure 4 Assuming a separate frame
 (1)
(1)
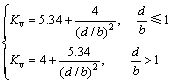 (2)
(2)
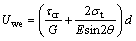 (3)
(3)
where σt is the yielding stress of the steel plate, E and G are the modulus of elasticity and the shear modulus, respectively, and q is the angle between the stresses of the diagonal tension field. For a representative element of the infill plate of the steel shear wall, the conditions of stresses in the steel plate before and after buckling are shown in Figure 5. In the present system, q is equal to a , as shown in Figure 3(b).
The induced stresses, as illustrated in Figure 5, are as follows:
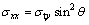 (4)
(4)
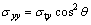 (5)
(5)
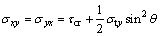 (6)
(6)
Thus, the shear force in the plate during buckling is
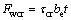 (7)
(7)
The displacement corresponding to the plate’s buckling shear force, in view of its pure shear behavior, can be obtained from relation 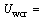
 By having the shear force and displacement of the plate, as well as its buckling force, the shear force-displacement diagram of the plate can be obtained, as illustrated in Figure 6. As is observed in this figure, points C and D indicate the buckling and yielding limits of the plate,respectively. For simplicity, lines OC and CD are replaced by line OD. Research has shown that such a substitution has a negligible effect.
By having the shear force and displacement of the plate, as well as its buckling force, the shear force-displacement diagram of the plate can be obtained, as illustrated in Figure 6. As is observed in this figure, points C and D indicate the buckling and yielding limits of the plate,respectively. For simplicity, lines OC and CD are replaced by line OD. Research has shown that such a substitution has a negligible effect.

Figure 5 Conditions of stresses in steel shear wall:

Figure 6 Shear load-displacement diagram of plate
Based on the von Mises criterion, a plate yields when the following relation is established.
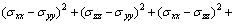
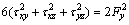 (8)
(8)
Since the thickness of the shear plate is small, the stresses will be considered plane stresses.
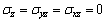 (9)
(9)
Therefore, Eq.(9) can be simplified as
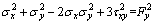 (10)
(10)
During the plate yielding, by considering the buckling and substituting the stress values, we will have
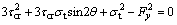 (11)
(11)
Thus, the equivalent yielding stress of the plate will be
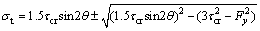 (12)
(12)
So, by considering the buckling and yielding of the plate, its shear strength will be
 (13)
(13)
Also, the onset of the shear plate’s plastic displacement, 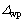 , is determined by equating the work of the shear force to the strain energy of the plate (U). Considering the effect of the diagonal tension field,
, is determined by equating the work of the shear force to the strain energy of the plate (U). Considering the effect of the diagonal tension field,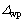 is computed as
is computed as
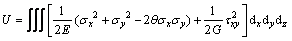 (14)
(14)
By ignoring the buckling strength of the plate, we get
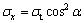 (15)
(15)
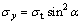 (16)
(16)
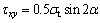 (17)
(17)
And by integrating Eq. (14), the strain energy is obtained as
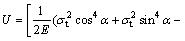
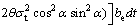 (18)
(18)
By considering a Poisson ratio of 0.3 and using the trigonometric relations, the above equation is simplified as
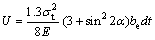 (19)
(19)
The work of the external force is equal to
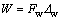 (20)
(20)
By equating the external work to the strain energy, the shear displacement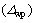 is determined as
is determined as
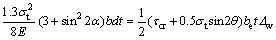 (21)
(21)
Therefore
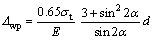 (22)
(22)
where be is the effective length of the angled plate that is equal to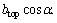
To get the frame’s shear force-displacement diagram, by assuming rigid beam-column joints and complete elasto-plastic behavior for the frame, the diagram of Figure 7 can be obtained by using Eqs. (23)-(25).
For the bending frame in the elastic region, stiffness is expressed as
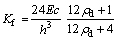 (23)
(23)
where 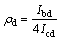 is the column-to-beam stiffness ratio, and Ibd and Icdare the moments of inertia of the beam and columns sections, respectively.
is the column-to-beam stiffness ratio, and Ibd and Icdare the moments of inertia of the beam and columns sections, respectively.
The frame’s shear force obtained after the formation of plastic hinges in the columns, Ff, represents the shear capacity or the ultimate shear force. Displacement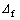 corresponds to the frame’s elastic limit displacement (onset of plastic displacement) and is equal to
corresponds to the frame’s elastic limit displacement (onset of plastic displacement) and is equal to
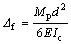 (24)
(24)
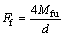 (25)
(25)
Thus, by having Eqs. (3), (22), (24) and (25), the load-displacement diagram of the steel shear plate for the elastic region can be sketched.
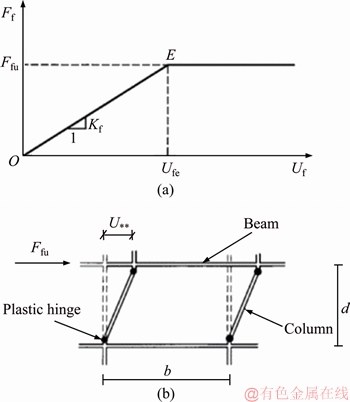
Figure 7 Required properties for drawing load-displacement of main frame
To plot the load-displacement diagram for the secondary columns (SE), the effect of the SE is taken into consideration. For this purpose, the ultimate strength and stiffness of the SE are calculated as follows:
For the bending frame in the elastic region, the stiffness is expressed as
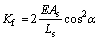 (26)
(26)
where As and Ls are the area section and the length of the secondary columns, respectively.
The shear force of the SC obtained after the formation of plastic hinges in the columns, Fse, represents the shear capacity or the ultimate shear force. Displacement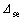 corresponds to the frame’s elastic limit displacement (onset of plastic displacement) and is equal to
corresponds to the frame’s elastic limit displacement (onset of plastic displacement) and is equal to
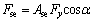 (27)
(27)
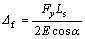 (28)
(28)
Therefore, the load-displacement diagram of the steel shear wall can be sketched as in Figure 8. The vertical diagram of the figure is shown in Figure 9.
4 Numerical study
4.1 Material and boundary condition
In this work, ST37 steel is used for all steel components. The yield stress is 240 MPa, the ultimate stress is 370 MPa and the modulus of elasticity is equal to 200 GPa for ST37. In addition, the von Mises criterion is chosen as an acceptable and valuable criterion with a precision for assessing the yield of the components. In the FE modeling, shell elements have been used to model all components. In addition, to create a proper connection to the laboratory conditions, the components are meshed in such a way that their nodes adhere to the joining site, so all the components in the vicinity are merged to create a complete connection.
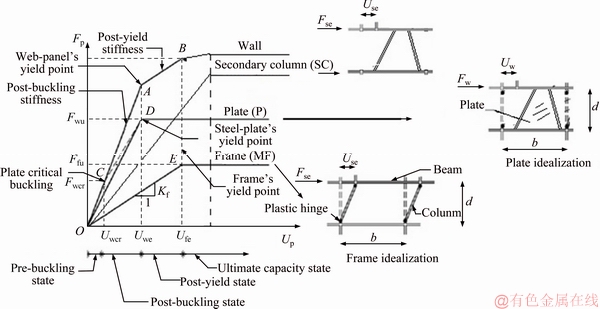
Figure 8 Load-displacement diagram of angled steel shear wall
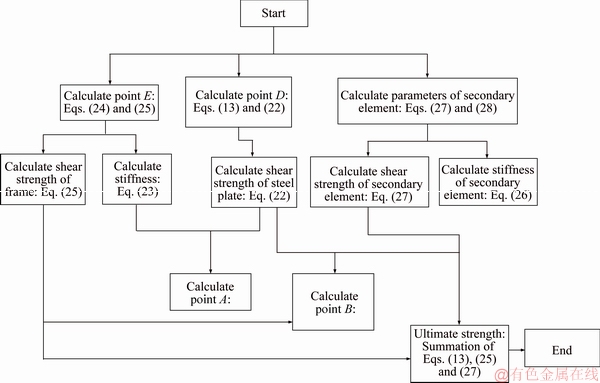
Figure 9 Vertical diagram to access load-displacement diagram of angled steel shear wall
Lateral loads are applied to the beam-column connections and are gradually increased from zero to a magnitude beyond the system’s capacity. The ultimate displacement limit is considered to occur at a drift ratio of 2.5% per ASCE 7-05 (ASCE, 2010). To simulate the fixed condition of the column-to-base plate connections, the bottom nodes of both columns’flanges and webs are restrained from displacement in all directions. To simulate the constraints imposed by slabs of the story floors, the out-of-plane displacements of the beam webs are also restrained.
4.2 Verification of numerical results
In order to verify the results of the FE modeling, an experimental test model from Ref. [21] has been selected to evaluate the accuracy of the FE modeling results. In the experimental model, the thickness of the steel plate, as well as the section of the beam, is 2 mm; the main column and the secondary column are IPE240, 2IPE160, 2UNP160. The geometric characteristics of the experimental model are shown in Figure 10. In the FE modeling, the mechanical properties of the steel materials are presented based on the experimental results of the software.
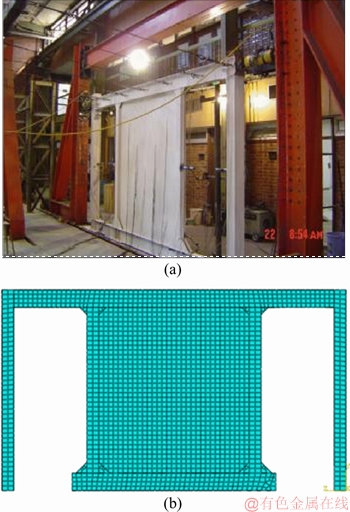
Figure 10 Setup of experimental test [22] (a) and finite element modeling (b)
In Figure 11, the load-displacement diagram of the FE model and the experimental model are compared, indicating the accuracy of the FE modeling. The FE modeling shows the final strength with very high accuracy; in the elastic region of the error, the error is about 6.5%.

Figure 11 Comparison of FE results with experimental results
4.3 Defining structural parameters
In order to estimate the seismic parameters, the actual load-displacement response curves are usually idealized, as illustrated in Figure 12. This idealization is based on the following assumptions and definitions:
1) The maximum displacement of structure Dmax will be considered based on the requirements of the local regulations.
2) The ductility factor is measured as m= Dmax/Dy from the ideal curve.
3) The elastic stiffness K is equal to the initial slope of the load-deformation curve 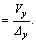
4) The over strength factor Ω is the reserved strength value existing between Vy and Vs, so response modification factor Ru is determined as 
4.4 Numerical models
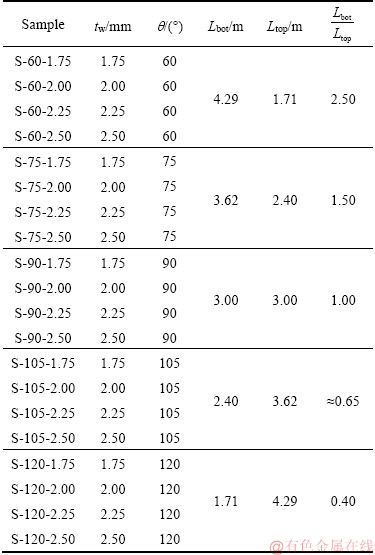
To evaluate the behavior of the proposed semi-supported steel plate shear walls, the FE models are evaluated using nonlinear analyses. The characteristics of the FE models are listed in Table 1.
In this table, the name of each model consists of three parts: the first part of the name is S, which represents the steel plate shear wall, the number in the second part represents the angle of e secondary column in degree, and the third part represents the thickness of the steel plate in mm. For example, S-60-1.75 means a shear wall with a 60° angle and a 1.75-mm steel plate. In the proposed models, 90°angles or semi-supported walls are considered as a comparison reference. In the numerical models, the S-90-1.75 model is selected as a benchmark model. As the conventional semi-supported wall is not supported in CODs, it is designed by means of equations presented in standard articles. By doing so, the S-90-1.75 model was designed based on the relationship presented by the researcher.
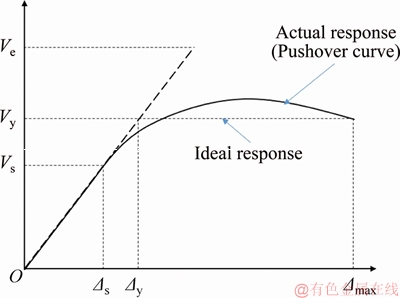
Figure 12 Idealization of load–displacement curve of structures
Table 1 Model properties
In all models, the area of the used plate is the same, so the volume of the same materials is used. It is an important investigation from an economical aspect. Since the material of all the models is the same, the model with better performance is the most economical wall. In Figure 13, the numerical models are presented schematically based on the given angles, θ=60°, 75°, 90°, 105° and 120°.
The angles smaller than 60° are not applicable. Figure 14 shows the wall with θ=45°. In this model, based on the angle of the wall, a small length for welding is provided in the top of the wall, where the infill plate is attached to the beam. In addition, at the bottom of the wall, a small length is provided that is not applicable in practical projects. So the wall should be limited to 60°≤θ≤120° based on practical considerations.
5 Discussion and results
5.1 Load-displacement curve
The load-displacement diagram contains valuable information on the structure’s performance such that seismic parameters can be extracted from this diagram. For this purpose, in Figure 15, the load-displacement diagram of the FE models is plotted. It can be seen from this figure that by reducing the angle, the elastic and inelastic zones are improved, and the ultimate strength, stiffness, and energy absorption are enhanced. This is also true for the increasing of the thickness. In the next sections, these parameters are evaluated more exactly.
5.2 Stiffness
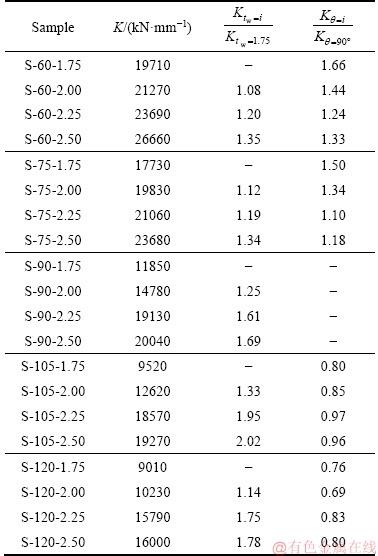
The most important parameter to control the lateral displacement and drift ratio is stiffness. Increasing the stiffness reduces the drift and consequently decreases the secondary moments. Structural stiffness shortage results in an increase in secondary moments due to the effects of P-Δ, which can lead to structural damage. For this reason, the elastic stiffness of the structures of the P-Δ FE is listed in Table 2. The results presented in this table show that increase in the thickness of the steel plate, as well as change in the angle of the secondary column, has a significant effect on the elastic stiffness. The reduction of the angle of the secondary columns causes a considerable rise in elastic stiffness. The increased stiffness for the angles of 60° and 75°, will be from 33% to 66% and from 18% to 50%, respectively, but by increasing the wall angle, the reduced stiffness of the wall for walls with angles of 105° and 120° will be from 4% to 20% and from 20% to 30%, respectively.
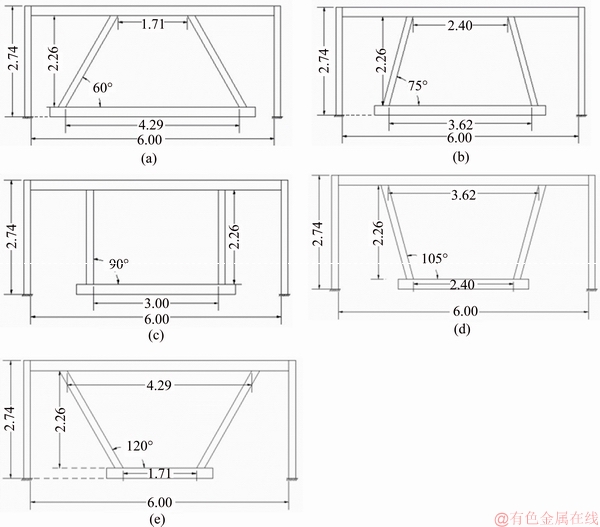
Figure 13 View of models with θ=60° (a), θ=75° (b), θ=90° (c), θ=105° (d) and θ=120° (e) (Unit: m)
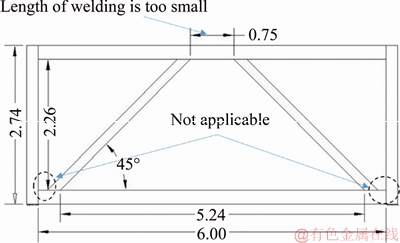
Figure 14 Wall with θ=45° (Unit: m)
However, the wall angle and the thickness of the steel plate do not have much effect on the stiffness of the non-elastic zone. As illustrated in Figure 16, stiffness dwindles for all walls in the drift ratio of 0.16%, which is due to the structural yield. In the drift ratio, about 0.5% of the stiffness tends to be zero, which is the sign of the zero gradient of the load-displacement diagram.
5.3 Ultimate strength
The ultimate strength of any seismic system is one of the important parameters in protecting a structure against earthquake. In order, the ultimate strength of the numerical models is shown in Figure 17 (and Table 3). The results show that increasing the thickness of the plate always causes an increase in the ultimate strength and reducing the angle of the wall also causes an increase in the ultimate strength. It is worth noting that plate angle changes are more important than plate thickness variations to achieve more resistance. By increasing the plate thickness from 1.75 mm to 2.5 mm, that is, a 42% increase in materials in the conventional wall (a 90° wall), we will have an up to 33% increase in resistance. However, keeping the plate thickness constant, it can be seen that at a 60° angle, resistance can be increased to 46%. This increase in ultimate strength reaches 22% for a 75° angle. In walls with angles of more than 90°, those with angles of 105° and 120°, we will have a minimum resistance of 5% and 12%, respectively. For walls with angles of 105° and 120°, resistance is reduced to 10% and 23%, respectively. Therefore, the use of walls with angles of 60° with constant material volumes will have a more favorable performance than conventional walls.
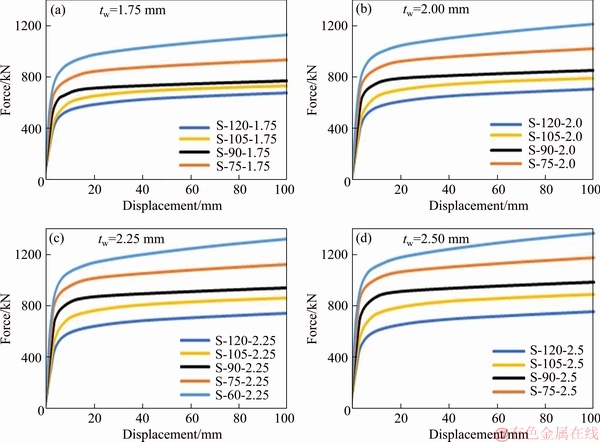
Figure 15 Load-displacement curve
Table 2 Elastic stiffness
5.4 Energy absorption
One of the most important seismic parameters of any structure is its energy absorption. The higher the energy absorption of the structure, the fewer forces it will experience during an earthquake. Therefore, higher energy absorption structures will show better performance during a severe earthquake. In order to assess the energy absorption, the idea of angled walls in Figure 18 and Table 4 lists the energy absorption of numerical models.
The results show that increasing plate thickness and also decreasing the angle of the plate always increases the energy absorption. By increasing the thickness of the plate from 14% to 42% (90° wall), energy absorption will be increased between 11% and 32%, but by keeping the thickness of the plate constant, the volume of the same materials in the wall at a 60°angle, the increase in energy absorption will be between 33% and 41%. In addition, this increase in energy absorption for the wall of 75° will be between 18% and 20%, and there will be a decreasing of energy absorption in walls with an angle of more than 90°. Therefore, 60° angle walls with a constant volume of materials relative to conventional walls will have a much more favorable performance.
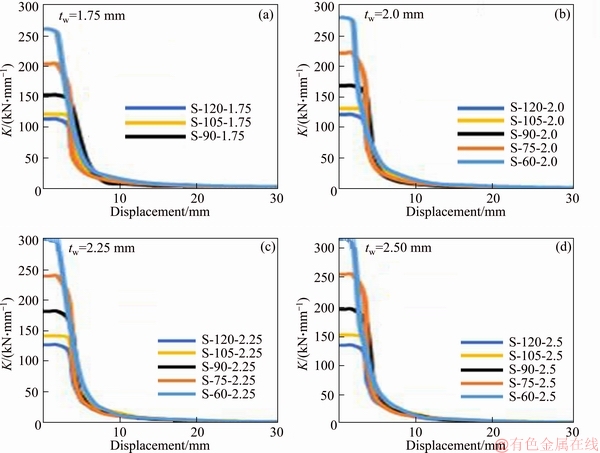
Figure 16 Stiffness versus displacement
Table 3 Ultimate strength
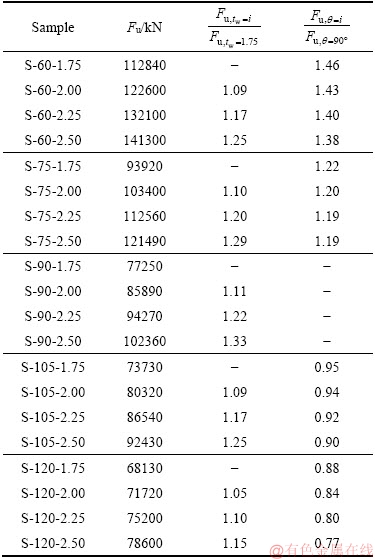
Figure 17 Ultimate strength
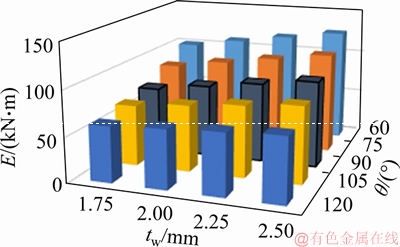
Figure 18 Energy absorption
Table 4 Energy absorption
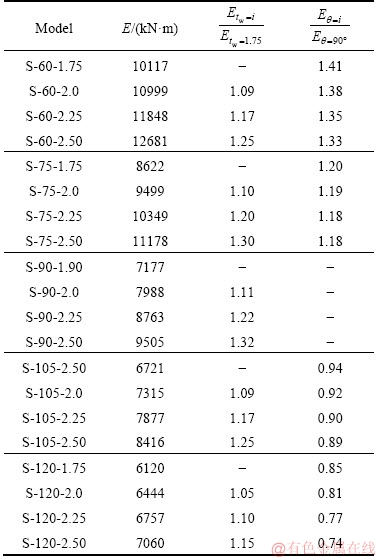
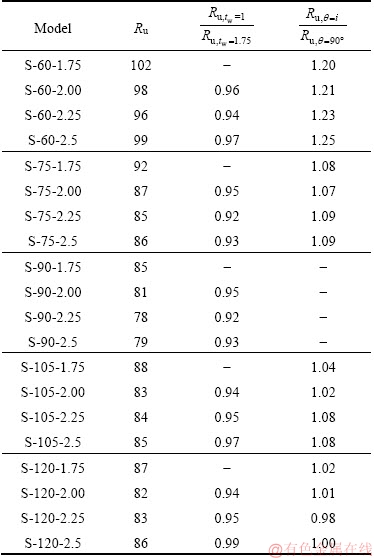
5.5 Modification factor
Systems with higher coefficients of behavior are important from economical aspects. The more the coefficient of behavior is, the more the structure is designed for less force. Therefore, they will cause to reduce the volume of consumables from an economical standpoint. In Table 5, the behavior coefficient is listed for all models. Comparison of the behavior coefficients shows that increasing the thickness of the plate causes a decrease in the behavior of the coefficient. On average, in all cases, the decrease of about 5% indicates that the decrease in the behavior coefficient is not significant. However, there is a significant increase in the behavior coefficient in the proposed wall (wall with a 60° degree angle), which increases the behavior coefficient from 20% to 25% relative to the thickness. It is noteworthy that with the increase in all angular walls, the increase of the behavior coefficient is obvious.
Table 5 Modification factor
5.6 Hinge formation at structural members
Figures 19–22 show the yield of the structure at the limit of the final displacements, which shows that in the walls with a 60° angle, the yield is concentrated in the steel plate and other structural components remain in the elastic region. In this model, in the beam at the junction with the secondary column, it is placed on the verge of the beginning of nonlinear behavior, which is negligible, according to the loading end stage. It can be said the main structural components remain in the elastic region. Therefore, walls with 60° angles can be loaded by changing displacements more than limited in regulations. However, in other systems, in addition to the steel plate, the plastic junction is formed by the main structure in which in most cases at the main column, the plastic junction is also formed. At walls with more than 90° angles the whole beam is yielded outside of the junction point to the shear which shows that the whole yielding of the  structure is at the displacement of the ultimate displacement change. The status of the yield in the finite element models certifies the performance of favorable vibration of suggested walls with 60°angle.
structure is at the displacement of the ultimate displacement change. The status of the yield in the finite element models certifies the performance of favorable vibration of suggested walls with 60°angle.
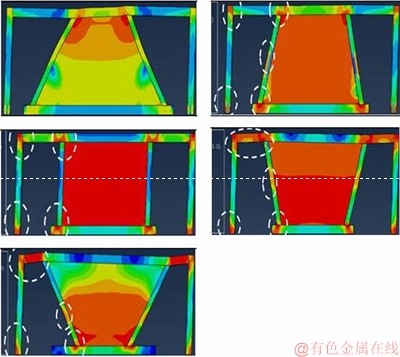
Figure 19 Hinge formation on walls with tw=1.75 mm
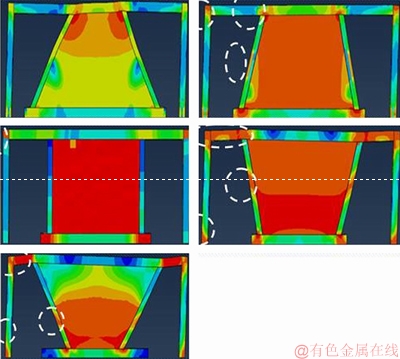
Figure 20 Hinge formation on walls with tw=2.00 mm
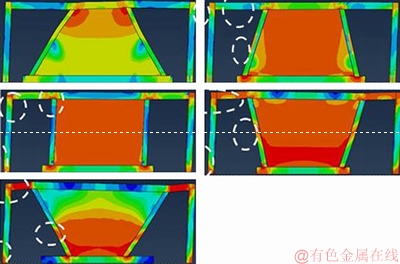
Figure 21 Hinge formation on walls with tw=2.25 mm
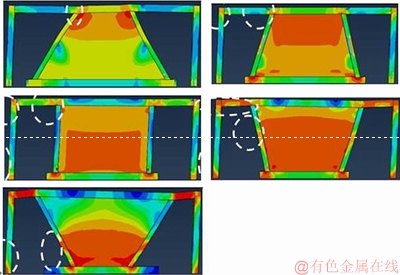
Figure 22 Hinge formation on walls with tw=2.50 mm
The stress on the walls with angles of 75°, 90° and 105° is greater than the yielding stress. When the stress on the infill plate reaches the yielding stress, hinges form at the main frame. The stress is here shown in red. Nevertheless, stresses on the wall with 60° angle yielded have been occurred in an area that other part of the infill plate can carry out of the lateral loading.
6 Accuracy of proposed method
The FE results were compared with the results of the proposed method (Figure 23), and the high accuracy of the proposed approach was confirmed by this comparison. As shown in Figure 23, the results of the proposed method in the elastic region completely match the finite element results for all models. In addition, the proposed method has a high convergence with the FE results for the reference model: S-60-1.75. If the thinness of the angled semi-supported SPSW increases, the accuracy of the proposed method is reduced in the nonlinear zones.Moreover, although the proposed method overestimates the strength in the plastic region, it still has adequate accuracy.
7 Conclusions
In this work, a new semi-supported steel shear wall was presented. Numerical results showed that the proposed system has a better performance than the conventional SPSW. The numerical results are summarized as follows:
1) Reducing the wall angle relative to the conventional wall improves the system’s behavior and also improves the seismic parameters. However, increasing its angle does not yield better performance than the conventional wall.
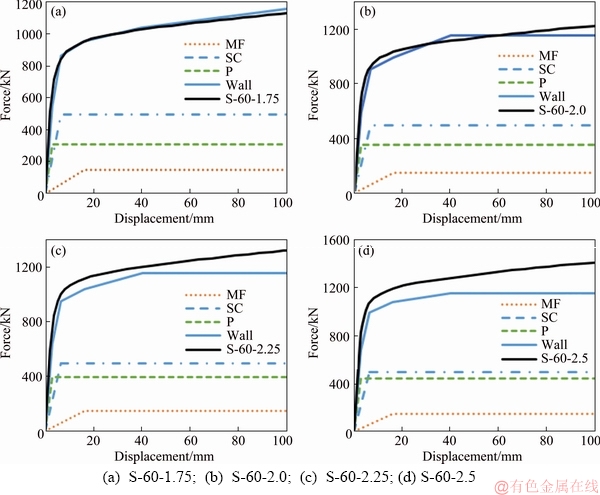
Figure 23 Comparison of pushover curve with the proposed model:
2) Comparison of seismic parameters shows that a wall with an angle of 60°, in regard to the economic and behavioral aspects, is optimal and efficient.
a) Increased stiffness for walls with angles of 60° and 75° is 33% to 66% and 18% to 50%, respectively, but there is a decreased stiffness for walls with angles of 105° and 120° of 4% to 20% and 20 % to 30%, respectively. But the angle of the wall has no significant effect on the non-elastic stiffness.
b) The results show that increasing the thickness of the plate as well as reducing the angle of the plate always increases the absorption of energy. By increasing the thickness of the plate from 14% to 42% (wall 90°), the energy absorption is enhanced from 11% to 32%. But in equal conditions, with an equal volume of materials, a wall with a 60° angle will increase the energy absorption from 33% to 41%. In contrast, the increased amount of energy absorption for the wall with an angle of 75 degrees will be between 18% and 20%.
c) By increasing the thickness of the plate from 1.75 mm to 2.5 mm, that is, a 42% increase in the material in the conventional wall (90° wall) (the maximum resistance will increase 33%), but in the wall with a 60° angle, maintaining the thickness of the sheet will increase the resistance 46%. In contrast, this amount of increase in ultimate strength reaches 22% for a 75° angle wall. In walls with an angle of more than 90°, i.e., walls with angles of 105° and 120°, we will have resistance reduced to a minimum of 5% and 12%, respectively. This resistance reduction is observed for walls with angles of 105° and 120° to 10% and 23%, respectively.
References
[1] KAHRAMAN A. Effect of axial vibrations on the dynamics of a helical gear pair [J]. Journal of Vibration and Acoustics, 1993, 115(1): 33–39.
[2] Broujerdian V, Ghamari A, Ghadami A. An investigation into crack and its growth on the seismic behavior of steel shear walls [J]. Thin-Walled Structures, 2016, 101: 205–212.
[3] Broujerdian V, Shayanfar M A, Ghamari A. Corner crack effect on the seismic behavior of steel plate shear wall system [J]. Civil Engineering Infrastructures Journal, 2017, 50 (2): 311–332.
[4] Hatami F, Ghamari A, Rahai A. Investigating the properties of steel shear walls reinforced with carbon fiber polymers (CFRP) [J]. Journal of Constructional Steel Research, 2012, 70: 36–42.
[5] Lanhui G, Rongb Q, Quc B, Liud J. Testing of steel plate shear walls with composite columns and infill plates connected to beams only [J]. Engineering Structures, 2017, 136: 165–179.
[6] Wang P, Xue Z, Xiao S. Seismic behavior of self-buckling-restrained steel plate shear wall made by two incline-slotted infill plates [J]. Journal of Constructional Steel Research, 2017, 133: 47–64.
[7] Lv Yang, Li Zhong-xian, Lu Guo-xing. Shear capacity prediction of steel plate shear walls with precompression from columns [J]. The Structural Design of Tall and Special Buildings, 2017, 26, e1375.
[8] Jiang L, Zheng H, Hu Y. Experimental seismic performance of steel- and composite steel-panel wall strengthened steel frames [J]. Archives of Civil and Mechanical Engineering, 2017, 17: 520–524.
[9] Ozcelik Y, Clayton P M. Seismic design and performance of SPSWs with beam-connected web plates [J]. Journal of Constructional Steel Research, 2018, 142: 55–67.
[10] Wei M W, Liew J Y R, Yong D, Fu X Y. Experimental and numerical investigation of novel partially connected steel plate shear walls [J]. Journal of Constructional Steel Research, 2017, 132: 1–15.
[11] Shekastehband B, Azaraxsh A, Showkati H. Experimental and numerical study on seismic behavior of LYS and HYS steel plate shear walls connected to frame beams only [J]. Archives of Civil and Mechanical Engineering, 2017, 1: 154–168.
[12] Zhou Y, Lu X, Dong Y. Seismic behavior of composite shear walls with multi-embedded steel sections, Part I: experiment [J]. The Structural Design of Tall and Special Buildings, 2010, 19(6): 618–636.
[13] Claytona P, Bermanb J, Lowesb L. Seismic performance of self-centering steel plate shear walls with beam-only-connected web plates [J]. Journal of Constructional Steel Research, 2015, 106: 198–208.
[14] Kurata M, Leon R T, Roches R D, Nakashima M. Steel plate shear wall with tension-bracing for seismic rehabilitation of steel frames [J]. Journal of Constructional Steel Research, 2012, 71: 92–103.
[15] Hatami F, Ghamari A, Hatami F. Effect of fiber angle on LYP steel shear walls behavior [J]. Journal of Central South University, 2014, 21: 768-774.
[16] Chen S J, Jhang C H. Cyclic behavior of low yield point steel shear walls [J]. Thin-Walled Structures, 2006, 44: 730–738.
[17] Sabelli R, Bruneau M. Design Guide 20: Steel Plate Shear Walls [M]. American Institute of Steel Structures, 2006.
[18] Jahanpour A, Moharrami H. Evaluation of behavior of the secondary columns in semi-supported steel shear walls [J]. Thin-Walled Structures, 2015, 93: 94–101.
[19] Guo L, Rong Q, Ma X, Zhang S. Behavior of steel plate shear wall connected to frame beams only [J]. International Journal of Steel Structures, 2011, 11: 467–479.
[20] LI Bei-bei, WANG Jing-feng, LU Yong, ZHANG Zeng-de, WANG Jia-xin. Seismic response tests and analytical assessment of blind bolted assembly CFST frames with beam-connected SPSWs [J]. Engineering Structures, 2019, 178: 343–360.
[21] Moharrami H, Habibnejad korayem A. Advantages of thin steel shear wall for retrofitting of steel structures [J]. Journal of Steel Structures: In Persian, 2016, 4: 1–13.
[22] Shekastehband B, Azaraxsh A, Showkati H. Experimental and numerical study on seismic behavior of LYS and HYS steel plate shear walls connected to frame beams only [J]. Achieves of Civil and Mechanical Engineering, 2017, 17: 154–168.
(Edited by HE Yun-bin)
中文导读
半支撑钢板剪力墙的性能提升
摘要:最近的地震和实验研究表明钢板剪力墙(SPSW)的性能良好,但该系统的一个主要缺点是需要巨大的柱子来包围填充板,而利用半支撑SPSW可以解决这一不足。半支撑SPSW有二级柱,可防止应力从填充板转移到主柱。尽管对SPSW进行了大量的实验和数值研究,但关于半支撑SPSW的行为仍存在许多争议。虽然柱内的应力减小了,但填充板内形成了不完全的对角张力场作用,从而产生了新的问题。本文提出了一种新型的半支撑式钢结构,钢板和次柱之间形成一个夹角,使钢板的全部承载力和次柱的承载力得以利用。数值模拟结果表明,与半支撑墙体相比,60°角的墙体具有良好的性能。此外,当夹角为60°时,刚度、强度和能量吸收都有所增加。二次柱的角度对非弹性刚度影响不大。然而,若使用角度大于90°的墙将抵消相对于传统墙的优势。因此,推荐60°为墙体的最佳角度。
关键词:钢板剪力墙;延展性;刚度;极限强度;R因子
Received date: 2018-06-13; Accepted date: 2018-12-19
Corresponding author: Ali GHAMARI, PhD, Assistant Professor; Tel: +98-9183447561; E-mail: aghamari@alumni.iust.ac.ir; ORCID: 0000- 0003-4204-1743
Abstract: In spite of the good performance of the steel plate shear wall (SPSW) in recent earthquakes and experimental studies, the need for huge columns to surround the infill plate is a major shortcoming of the system. This shortcoming can be resolved by using semi-supported SPSW. The semi-supported SPSW has secondary columns that prevent the transfer of stress from the infill plate to the main columns. In spite of extensive experimental and numerical investigations on SPSWs, there are many ambiguities regarding the behavior of the semi-supported SPSW. Although stress in the columns is reduced, incomplete diagonal tension field action is formed in the infill plate that creates new problems. In this paper, a new type of semi-supported SPSW is presented in which the steel plate and the secondary columns are angled. The creation of the angle of the plate and the secondary column makes it possible to use the full capacity of the steel plate as well as the capacity of the secondary columns. Numerical results showed that the wall with a 60° angle has a favorable performance relative to the semi-supported wall. Moreover, with the 60° angle, stiffness, strength and energy absorption is increased. The angle of the secondary columns has little effect on the non-elastic stiffness. Nevertheless, using a wall with an angle of more than 90° can neutralize the wall’s behavior relative to conventional walls. Therefore, the wall with a 60° angle as an optimal angle is recommended.


