J. Cent. South Univ. (2017) 24: 1647-1653
DOI: 10.1007/s11771-017-3570-1
WANG Min(王敏)1, 2, CAO Ping(曹平)1, LI Rui-chao(李瑞超)1, FAN Xiang(范祥)3
1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;
2. Hunan Provincial Key Laboratory of Shale Gas Resource Utilization, Hunan University of Science and Technology, Xiangtan 411201, China;
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract:
Brazilian disc tests were undertaken on a number of red sandstone samples with different water absorption ratios. The tensile strength of the red sandstone decreases as the water absorption ratio increases. The fracture surfaces of failed red sandstone discs were scanned by Talysurf CLI 2000. With the aid of Talymap Gold software, based on ISO25178, a set of statistical parameters was obtained for the fracture surfaces. The maximum peak height (Sp), maximum pit height (Sv) and maximum height (Sz) of the fracture surfaces exhibited the same decreasing trend with increasing water absorption. Sa and Sku values for the fracture surfaces showed a downward trend as the water absorption ratio increased. The fractal dimensions of fracture surfaces were calculated and found to decrease as the water absorption ratio increased. Through analysis of PSD curves, the smallest dominant wavelength was observed to reflect the roughness of the fracture surfaces. Additionally, the results suggest that the roughness of fracture surfaces becomes small as the water absorption ratio increases.
Key words:
water absorption ratio; Brazilian disc test; fracture surface; morphological analysis; roughness;
1 Introduction
Rock masses are generally not intact, but rather are full of many sets of joints and fracture surfaces that are well known to influence the engineering stability of the rock mass. Therefore, the investigation of the basic parameters of joints and fracture surfaces has attracted much attention [1, 2]. One of the key issues that need to be addressed is the morphology of the fracture surfaces.
It is generally accepted that the failure of brittle rock initiates from the tips of cracks because of tensile strength [3-5]. Moreover, crack propagation and rock strength are influenced by the rock’s water absorption ratio [6]. Once a fracture surface forms in rock, the mechanical and hydraulic properties of the rock will be strongly influenced by joints and fracture surfaces [7-9]. Because of the importance of the morphology of rock fracture surfaces in defining the mechanical and hydraulic behavior of the rock, a great number of methods have been developed to characterize the roughness of rock profiles. BARTON and CHOUBEY [10] defined 10 typical rock profiles with different joint roughness co-efficient (JRC) values; we can therefore assign a JRC value for a rock profile by comparing it with the 10 typical profiles. TSE and CRUDEN [11] established an empirical formula between JRC value and the root mean square of first derivatives (Z2). However, YU and VAYSSADE [12] found that the calculated JRC values were dependent on the sampling interval. The fractal dimension is another useful tool for quantifying the roughness of a rock profile [13, 14]. Both fractal dimension and JRC value are practical parameters that can be used to quantify the roughness of a rock profile. Some empirical formulas relating fractal dimension to JRC values have been put forward [15]. The study mentioned above mainly focused on two dimensions, which are different to three-dimensional (3-D) natural rock surfaces. Much research in recent years has focused on 3-D fracture surfaces, and some successes have been made in evaluating the roughness of 3-D fracture surfaces [16, 17].
In this work, fracture surfaces were obtained by the Brazilian disc test with plane loading platens. The tensile strength of the red sandstone with different water absorption ratios was calculated and its changing trend was analyzed. Subsequently, the fractured surfaces of the discs were scanned by the Talysurf CLI 2000. With the help of the Talymap Gold software, the maximum peak height, maximum pit height, fractal dimension and other parameters of the fracture surfaces were calculated and the results were analyzed in detail. These analyses lay a solid foundation for the further study of the mechanical and hydraulic behavior of rock containing fracture surfaces.
2 Specimen preparation and laboratory tests
2.1 Water absorption measurements
Red sandstone was selected for the laboratory experiments that tested Brazilian discs with a diameter of 0.05 m and a thickness of 0.05 m. Before soaking in water, the masses of the Brazilian discs were measured with an electronic balance. The red sandstone specimens were then soaked in water for varying periods of 2, 4, 6, 8, and 10 h, respectively. The mass of each Brazilian disc was remeasured after soaking in water, and the water absorption of red sandstone could be obtained by
 (1)
(1)
where ma is the mass of the Brazilian disc after soaking in water; md is the mass of Brazilian discs before soaking in water; wa is the water absorption ratio. The specimens’ water absorption ratios are listed in Table 1.
Table 1 Water absorption ratio of red sandstone samples

These Brazilian discs with various amounts of water absorption ratios were used to conduct the Brazilian disc tests. The plane loading platens were used to conduct the Brazilian disc tests. The discs were in direct contact with the loading platens and the loading ratio was 100 N/s. In the experiments, the friction between the loading platen and the Brazilian discs was ignored.
2.2 Tensile strength calculation
Through the Brazilian disc tests, the tensile strengths of red sandstone with different water absorption ratios were obtained. It is assumed that the friction between the loading platens and the discs is ignored and then the tensile strength obtained by Brazilian disc tests can be expressed as follows:
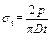 (2)
(2)
where σt is the tensile strength; p is the applied load; D is the diameter of Brazilian disc; t is the thickness of Brazilian disc.
2.3 Fracture surface scanning
After the Brazilian disc tests, the failed Brazilian discs and their fracture surfaces were obtained. The fracture surfaces of the failed specimens can be observed in Fig. 1.

Fig. 1 Fracture surfaces of failed red sandstone with various water absorption ratios
The fracture surfaces of the failed samples (six fracture surfaces in total) were scanned by Talysurf CLI 2000. The dimensions of the Talysurf CLI 2000 unit are 0.8 m×0.5 m×0.5 m, and the maximum mass of the specimen scanned by the machine is 30 kg. The accuracy of the machine can reach 0.5 μm (in the x, y, z directions), which guarantees results’ accuracy. Additionally, the maximum scanning speed is 30 mm/s and the scanner picks several points along the scanning direction. The scanning direction is detailed in Fig. 2.
3 Result analysis
3.1 Tensile strength varying with water absorption ratio

Fig. 2 Scanning direction
Based on Eq. (2), the tensile strength changing trend of the red sandstone with various water absorption ratio is shown in Fig. 3.
As illustrated in Fig. 3, the tensile strength of red sandstone exhibited a downward trend with increasing water absorption ratio. Red sandstone is mainly composed of particles and pores. When the red sandstone was soaked in water, water seeped into the pores gradually. Some cement of sandstone dissolved into water, hence the particles cementation of particles in sandstone was waken, which given rise to the decreasing of tensile strength. Hence, the absorbed water in the red sandstone weakens the tensile strength.
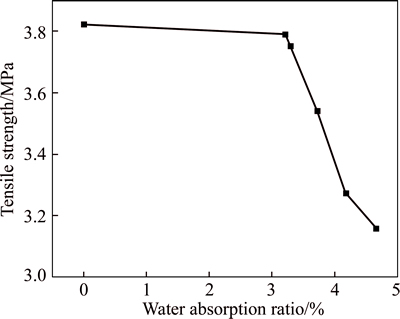
Fig. 3 Tensile strength of red sandstone with increasing water absorption ratio
3.2 Morphological analysis of fracture surfaces for Brazilian discs with different water absorption ratio
Surface morphologies were analyzed by using Talymap Gold software. The calculation method can be found in the software users’ manual and the definitions of the parameters are based on ISO25178. On the basis of the scanning results of the fracture surfaces of the red sandstone, the 3-D profiles of fracture surfaces are displayed in Fig. 4.
3.2.1 Theoretical introduction of statistical parameters
1) Maximum peak height (Sp)
The maximum peak height is the height between the highest peak and the mean plane, which can be denoted as follows:
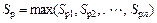 (3)
(3)
where Sp1, Sp2, …, Spn are the distances between individual peaks and the mean plane.
2) Maximum pit height (Sv)
The maximum pit height is the distance between the mean plane and the deepest valley, which can be expressed as
 (4)
(4)
where Sv1, Sv2, …, Svn represent the distances between the mean plane and the valleies.
3) Maximum height (Sz)
The maximum height is the distance between the highest peak and the deepest valley, which can be calculated by the following equation:
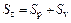 (5)
(5)
4) Arithmetical mean height (Sa)
The arithmetical mean height is the mean surface roughness. Its magnitude can be obtained by the following equation:
 (6)
(6)
where A is the horizontally defined area of the fracture surface; z(x,y) is the height function describing the fracture surface.
5) Kurtosis (Sku)
The kurtosis of the height distribution is the fourth statistical moment, qualifying the flatness of the height distribution. However, because of the large exponent used, this parameter is very sensitive to sampling and the noise of the measurement. The kurtosis of the height distribution can be calculated based on the following equation:
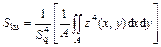 (7)
(7)
where Sq is the standard deviation of the height distribution; A is the horizontally defined area of the fracture surface; z(x,y) is the height function describing the fracture surface.
6) Fractal dimension of fracture surfaces
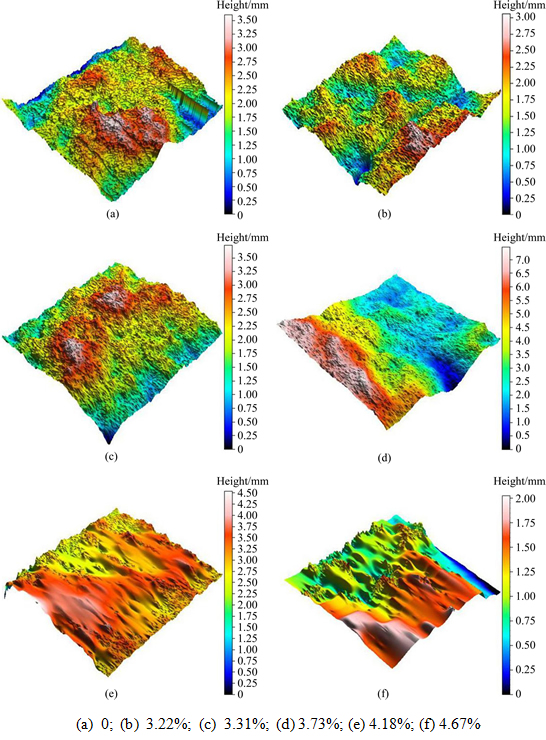
Fig. 4 3-D profiles for fracture surfaces of red sandstone with different water absorption ratios
Fractal geometry was invented by the French mathematician, BENOIT MANDELBROT [18-20], to describe the phenomenon of scale invariance. From pure theory, fractals have become progressively important tools in a large number of scientific fields. The fractal dimension concept enables the complexity of a surface to be described in the form of a single number.
There are several ways to calculate the fractal dimension of a surface or profile and each method has its advantages and drawbacks. The Talymap Gold software includes two calculation methods: boxes and morphological envelopes. In this work, the boxes method was used to calculate the fractal dimension of the fracture surfaces.
The boxes method consists of enclosing each section of a profile using a box with a width ε and a calculated total area Aε that encloses the whole profile. This procedure is iterated with boxes of different widths to graph the relationship ln(Aε)/lnε. The slope for line ln(Aε)/lnε would be the fractal dimension of the fracture surface. Figure 5 presents the fractal dimension of the fracture surfaces of the red sandstone with water absorption ratio of 3.31%.
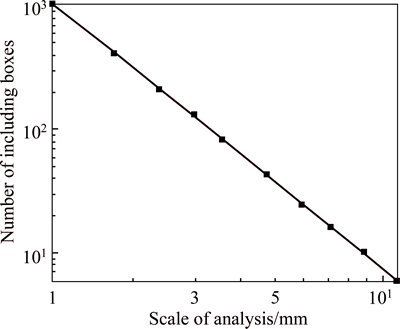
Fig. 5 Fractal dimension calculations of fractured surface of red sandstone with water absorption ratio of 3.31% and a fractal dimension of 2.33
7) Power spectral density study of fractured surfaces
Spectral analysis enables you to determine the periodicity and orientation of certain motifs that exist in the spectrum. This spectrum is obtained using the Fourier transform. The Fourier transform is used in many fields of science and engineering. The Fourier transform is a mathematical operation enabling you to visualize the frequencies (or wavelengths) of a signal. It is used as a mathematical or physical tool to transform a problem difficult to solve (in the time or spatial domain) into one that can be easily solved (in the frequency domain). The FFT (fast Fourier transform) is a Fourier transform algorithm optimized for a number of points equal to a power of 2.
For averaged power spectral density(PSD), the horizontal axis is graduated in wavelengths. The values above the peaks show the dominant wavelengths; the corresponding amplitude is displayed between brackets. The vertical axis displays the amplitude to a power of 2. The averaged power spectral density can be obtained by both the all directions method and the horizontal method. For all directions methods, the PSD curve corresponds to the mean spectrum calculated from the individual spectrum curves for all directions. However, only motifs that are visible on the x-axis (example: vertical furrows) will be shown by the horizontal method. Horizontal furrows are not visible as the PSD curve is calculated on each line (x-profile); the results are then added together. In this work, the averaged power spectral density of fracture surface was obtained by the horizontal method.
In averaging and smoothing curves, the inverted axis creates a problem: the wavelengths found in the spectrum are no longer regularly spaced. For a profile of length L, frequency f(1) corresponds to the wavelength f(1)=L, frequency f(2) to the wavelength f(2)=L/2, and frequency f(n) to the wavelength f(n)=L/n. Note that there are few long but many short wavelengths to be found in the spectrum.
To display the PSD in the form of a smooth curve that is as detailed in long as it is in short wavelengths, the spectrum is calculated several times using a Fourier transform on portions of the profile with different lengths. The contributions of the various spectra are then summed.
Sometimes, it is necessary to increase the size of the representation of the low frequencies (long wavelengths) that provide less information. If high frequencies (short wavelengths) are required, a magnification factor will be needed because these frequencies may be invisible when other magnifications are used. Figure 6 illustrates the power spectral diagram of a fracture surface of red sandstone with water absorption ratio of 4.67%.
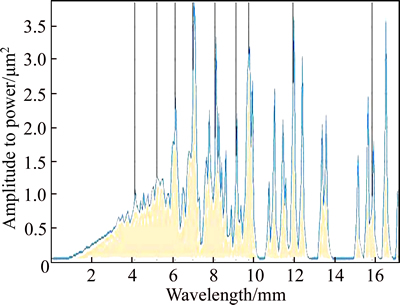
Fig. 6 Power spectral diagram of a sandstone fracture surface with water absorption ratio of 4.67%
3.2.2 Morphological analysis of fracture surfaces
Based on the calculation method presented above, the statistical parameters were calculated. A detailed analysis is as follows.
Figure 7 illustrates the changing trends of Sp, Sv, Sz, Sa, and Sku values as the water absorption ratio varies. Obviously, the values of Sp, Sv, Sz, Sa, and Sku are influenced by the water absorption ratio as they present an overall downward trend. Based on its definition, the value of Sz is the sum of Sp and Sv. Hence, Sp, Sv and Sz are closely related to each other. However, the values of Sp and Sv are sensitive to the height of the fracture surfaces, while the value of Sz is the difference between the highest peak and the deepest valley, which means that it can reflect fluctuations in the magnitude of fracture surfaces. The parameter Sa is the mean surface roughness and reflects the fluctuation in fracture surfaces. An observation of the changing trend in the Sa value shows that the fluctuation decreases. Based on the definition of Sku, the parameter is positively correlated with Sa.
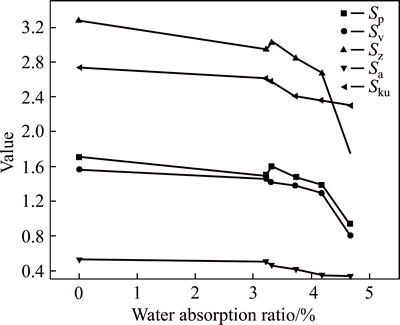
Fig. 7 Changing trends of Sp, Sv, Sz, Sa and Sku with variations in water absorption ratio
The smaller the roughness value for the fracture surfaces, the lower the standard deviation of the height distribution. That is to say, the fluctuation of the fracture surface becomes small. According to the analysis above, the fluctuation of fracture surfaces is observed to decrease with increasing water absorption ratio. In other words, the roughness of the fracture surfaces becomes small as the water absorption ratio increases because with the increasing of the water absorption ratio, the strength between particles of the red sandstone is weaken; consequently, the fracture surface becomes more uniform.
Fractal dimensions enable the description of surface complexity as a single number. For example, the fractal dimension of a planar area is 2 and of a volume is 3. In comparison, for fracture surfaces, the flatter the fracture surface is, the closer it will be to 2 and the rougher the fracture surface is, the closer it will be to 3. Figure 8 shows the variation of fractal dimensions as water absorption ratios increase. As water absorption ratios increase, the fractal dimensions (i.e., roughnesses) of the fracture surfaces are observed to become small. The fracture surfaces are closer to a plane (fractal dimension of 2) with high water absorption ratios. Obviously, the fractal dimension is strongly affected by the water absorption ratio.
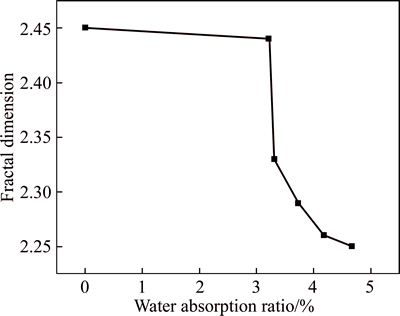
Fig. 8 Fractal dimension variation with increasing water absorption ratio
Based on the definition of a PSD, frequencies and wavelengths are negatively correlated. Hence, in PSD curves, the smallest wavelengths correspond to the highest frequencies. Therefore, the smallest dominant wavelength plays a critical role in describing the roughness of fracture surfaces. Figure 9 shows the smallest dominant wavelength of the fracture surfaces as they vary with water absorption ratios. As the water absorption ratio increases, the smallest dominant wavelength decreases. In other words, as the corresponding frequencies increase, the points on the fracture surface are closer to a constant value. Consequently, as the water absorption ratio increases, the roughness of fracture surfaces becomes smaller.
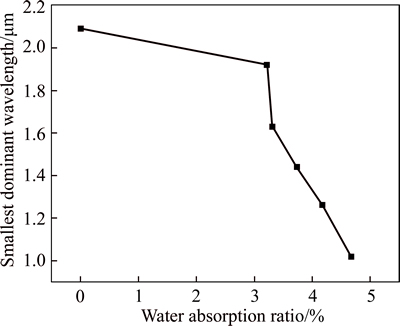
Fig. 9 Variation of smallest dominant wavelength with water absorption ratio increasing
4 Conclusions
1) The tensile strength of red sandstone decreases as the water absorption ratios increase. Red sandstone is mainly composed of particles and pores. When the red sandstone was soaked in water, water seeped into the pores gradually. Some cement of sandstone dissolved into water; hence, the particles cementation of particles in sandstone was waken, which gives rise to the weakness of tensile strength.
2) Through the Brazilian disc test, fractured surfaces of red sandstone with various water absorption ratios were produced. Using Talymap Gold software, parameters describing the roughness of fracture surfaces were calculated. The trend of Sp, Sv, Sz, Sa and Sku, the fractal dimension and the smallest wavelength value were all observed to decrease as the water absorption ratio increased.
3) The statistical parameters Sp, Sv and Sz are closely connected with each other because of their definitions. However, the values of Sp and Sv are correlated with the height of the fracture surface, which is independent of its roughness. Therefore, it is not surprising that the values of Sp and Sv do not show a monotonically decreasing trend. The parameter Sz reflects the difference in elevation between the highest peak and the deepest valley. So, it is a simple parameter to describe roughness without considering the distribution of all points on a fracture surface. Because the parameters Sa and Sku consider the standard deviation of the height distribution, they can reflect the roughness of fracture surfaces more accurately than parameters Sp and Sv. The changing trends in these parameters suggest that the roughness of fracture surfaces becomes small as the water absorption ratio increases.
4) Fractal dimension, the parameter describing the complexity of fracture surfaces, can be used to describe roughness. The rougher the fracture surface is, the closer to 3 the fractal dimension will be. The variation in fractal dimension indicates that the roughness of a fracture surface becomes small as the water absorption ratio increases. In the PSD curve, the frequencies and wavelengths are negatively correlated. Therefore, the smallest dominant wavelength plays a key role in characterizing the roughness of a fracture surface. As the water absorption ratio increases, the lowest dominant wavelength decreases. Through analysis of the PSD curves, the roughness of a fracture surface is observed to decrease as the water absorption ratio rises.
5) The morphology analysis of the fracture surfaces was conducted in detail, which provides the basis for the further study of the seepage regulations of the fracture surfaces. Combined the study on the morphology of the fracture surfaces, the seepage experimental study would conducted with consideration of the roughness of the fracture surfaces, it will be our next task.
References
[1] JANG H S, JANG B A. New method for shear strength determination of unfilled, unweathered rock joint [J]. Rock Mechanics and Rock Engineering, 2015, 48(4): 1515-1534.
[2] OGILVIE S R, ISAKOV E, GLOVER P W J. Fluid flow through fractures in rocks II: a new matching model for rough rock fractures [J]. Earth and Planetary Science Letters, 2006, 241: 454-465.
[3] YANG S Q, JING H W. Strength failure and crack coalescence behavior of brittle sandstone samples containing a single fissure under uniaxial compression [J]. International Journal of Fracture, 2011, 168(2): 227-250.
[4] YANG S Q, DAI Y H, HAN L J, JIN Z Q. Experimental study on mechanical behavior of brittle marble samples containing different flaws under uniaxial compression [J]. Engineering Fracture Mechanics, 2009, 76(12): 1833-1845.
[5] AL-SHAYEA N A. Crack propagation trajectories for rocks under mixed mode I-II fracture [J]. Engineering Geology, 2005, 81(1): 84-97.
[6] FREIRE-LISTA D M, FORT R, VARAS-MURIEL M J. Freeze-Thaw fracturing in building granites [J]. Cold Regions Science and Technology, 2015, 113: 40-51.
[7] KLAWITTER M, ESTERLE J, COLLINS S. A study of hardness and fracture propagation in coal [J]. International Journal of Rock Mechanics and Mining Sciences, 2015, 76(1): 237-242.
[8] LIANG L X, XIONG J, LIU X J. Experimental study on crack propagation in shale formations considering hydration and wettability [J]. Journal of Natural Gas Science and Engineering, 2015, 23: 492-499.
[9] YU S, ZHU W S, YANG W M, ZHANG D F, MA Q S. Rock bridge fracture model and stability analysis of surrounding rock in underground cavern group [J]. Structural Engineering and Mechanics, 2015, 53(3): 481-495.
[10] BARTON N, CHOUBEY V. The shear strength of rock joints in theory and practice [J]. Rock Mech, 1977, 10: 1-54.
[11] TSE R, CRUDEN D M. Estimating joint roughness coefficients [J]. Int J Rock Mech Min Sci & Geomech Abstr, 1979, 16(5): 303-307.
[12] YU X, VAYASSDE B. Joint profiles and their roughness parameters [J]. Int J Rock Mech Min Sci & Geomech Abstr, 1991, 28(4): 333- 336.
[13] KULATILAKE P, BALASINGAM P, PARK J, MORGAN R. Natural rock joint roughness qualification through fractal techniques [J]. Geotech Geol Eng, 2006, 24: 1181-1201.
[14] KULATILAKE P, UM J. Requirements for accurate quantification of self-affine roughness-length method [J]. Int J Rock Mech Min, 1999, 36: 5-18.
[15] LEE Y H, CARR J R, BARS D J, HAAS C J. The fractal dimension as a measure of the roughness of rock discontinuity profiles [J]. Int J Rock Mech Min Sci & Geomech Abstr, 1990, 27(6): 453-464.
[16] GRASSELLI G, WIRTH J, EGGER P. Quantitative three- dimensional description of a rough surface and parameter evolution with shearing [J]. Int J Rock Mech Min Sci & Geomech Abstr, 2002, 39(6): 789-800.
[17] HIROTAKA S, GRASSELLI G. Geostatistical downscaling of fracture surface topography accounting for local roughness [J]. Acta Geotech, 2010, 5: 127-138.
[18] GIRI A, TARAFDAR S, GOUZE P, DUTTA T. Fractal geometry of sedimentary rocks: simulation in 3-D using a relaxed bidisperse ballistic deposition model [J]. Geophysical Journal International, 2013, l 192(3): 1059-1069.
[19] PI W L, DAI G F. Research on periodical damage of roof rock-mass and its fractal character [J]. Disaster Advances, 2010, 3(4): 459-461.
[20] XIE H P, LIU J F, JU Y, LI J, XIE L Z. Fractal property of spatial distribution of acoustic emissions during the failure process of bedded rock salt [J]. Int J Rock Mech Min Sci, 2011, 48(8): 1344-1351.
(Edited by YANG Hua)
Cite this article as:
WANG Min, CAO Ping, LI Rui-chao, FAN Xiang. Effect of water absorption ratio on tensile strength of red sandstone and morphological analysis of fracture surfaces [J]. Journal of Central South University, 2017, 24(7): 1647-1653.
DOI:https://dx.doi.org/10.1007/s11771-017-3570-1Foundation item: Project(E21527) supported by Open Research Fund Program of Hunan Provincial Key Laboratory of Shale Gas Resource Utilization, Hunan University of Science and Technology, China; Projects(51174088, 51174228) supported by the National Natural Science Foundation of China; Project(2013CB035401) supported by the National Basic Research Program of China; Project(2015zzts077) supported by the Fundamental Research Funds for the Central Universities, China
Received date: 2015-11-23; Accepted date: 2016-10-06
Corresponding author: WANG Min, PhD Candidate; Tel: +86-15073218915; E-mail: michaelwong307@outlook.com
Abstract: Brazilian disc tests were undertaken on a number of red sandstone samples with different water absorption ratios. The tensile strength of the red sandstone decreases as the water absorption ratio increases. The fracture surfaces of failed red sandstone discs were scanned by Talysurf CLI 2000. With the aid of Talymap Gold software, based on ISO25178, a set of statistical parameters was obtained for the fracture surfaces. The maximum peak height (Sp), maximum pit height (Sv) and maximum height (Sz) of the fracture surfaces exhibited the same decreasing trend with increasing water absorption. Sa and Sku values for the fracture surfaces showed a downward trend as the water absorption ratio increased. The fractal dimensions of fracture surfaces were calculated and found to decrease as the water absorption ratio increased. Through analysis of PSD curves, the smallest dominant wavelength was observed to reflect the roughness of the fracture surfaces. Additionally, the results suggest that the roughness of fracture surfaces becomes small as the water absorption ratio increases.


