定点小数乘法器的低功耗算法与实现技术
袁博,刘红侠
(西安电子科技大学 微电子学院,宽禁带半导体材料与器件国家重点实验室,陕西 西安,710071)
摘 要:
端设计中的定点小数乘法器,提出一种既能够优化其内部加法器数量又能优化各级加法结果位宽的低功耗算法,而且在算法的实现技术上,解决目前低功耗设计中算法自身逻辑单元引入被优化系统从而降低系统优化效果的问题。在介绍该算法的理论基础和实现细节后,为了取得更加客观、更具有统计特性的低功耗优化效果,以该算法对某含有大量不同类型小数乘法器的射频模块进行优化。优化后FPGA测试结果显示逻辑占用率降低了39.3%,寄存器总数降低了45.0%,内存占用率降低了36.9%。该算法是一种高效的低功耗算法,并且解决了一般算法实现技术的缺陷与不足,其适用于对含有大量小数乘法运算的系统进行低功耗优化,例如数字信号处理和数字滤波器等。
关键词:
定点小数乘法;加法器数量;位宽;缺省;逻辑单元;功耗;面积;
中图分类号:TN702;TN402 文献标志码:A 文章编号:1672-7207(2014)01-0132-10
Low power methodology and implementation for fixed-point decimal multiplier
YUAN Bo, LIU Hongxia
(Key Lab of Ministry of Education for Wide Band-Gap Semiconductor Devices, School of Microelectronics,
Xidian University, Xi’an 710071, China)
Abstract: A low power methodology for fixed-point decimal multiplier in IC design was presented to optimize the number and width of the adders that were inside of synthesized multiplier. In terms of methodology implementation, it resolved the problem of optimization logic joining into optimized system, which existed in present low power design. The theoretical basis and the design method were explained. In order to get more objective and statistical test result, the methodology and implementation were used to optimize a radio-frequency module. FPGA test results show that logic utilization is reduced by 39.3%, the total number of registers used is reduced by 45.0%, and the total block memory bits utilization is reduced by 36.9%. These results show that the proposed low-power design is an effective method, which has good performance on optimizing the system including large-scale decimal multipliers, such as DSP and digital filter.
Key words: fixed-point decimal multiplication; number of addition; width; omit; logic cell; power consumption; area
随着VLSI(超大规模集成电路)设计技术的进步,高性能处理芯片已经成为通信、电子、空间技术等领域必不可少的组成部分。因此,含有大量小数乘法运算的模块也被频繁地应用于各种芯片和电路中,例如数字滤波器及数字信号处理器等等。对于一般乘法运算,其功耗和面积主要来源于内部加法运算数量,因此若能够在保持乘法运算准确度的前提下减少其内部加法运算数量,则可以有效降低该乘法器的功耗和面积[1]。而对于定点小数乘法运算,为了保持较高的运算精度,必然要求其内部寄存各级加法运算结果的寄存器保持较宽的位宽,但同时会导致系统功耗和面积变大;反之,若试图减小内部各寄存器位宽来降低整个乘法器的功耗和面积,则乘法运算的精度损失将不可避免[2]。现阶段低功耗设计中,人们往往希望通过降低系统时钟频率、减少冗余信号翻转等方法来降低系统功耗。其中降低系统时钟频率会有效降低系统功耗,但系统性能和工作效率也会随之降低;而减少冗余信号翻转虽然不会影响系统性能,但需要在系统中增加额外控制电路,这会使得系统引入额外的功耗和面积。常见的低功耗设计有:
(1) 门控时钟。其主要采用触发器的设计方法,即当触发器状态出现冗余翻转时,通过关闭时序部件的时钟,使触发器保持静态,同时以这些时序部件输出为输入信号的组合逻辑也将处于静态,可以实现降低功耗的作用[3]。该方法的缺点是需要在时序部件的时钟输入端加入控制逻辑,使其能够在部件处于冗余状态时关闭输入时钟,即在降低部件功耗的同时引入控制逻辑带来的额外的功耗,影响部件低功耗优化效果。
(2) 操作数隔离。其优化对象是系统中的算术、逻辑运算模块,主要方法是在系统处于冗余状态下,即不进行算术、逻辑运算的时候,使模块的所有输入保持“0”,禁止操作数进入系统产生冗余信号翻转,该方法使系统输出结果保持静止。而当系统需要进行运算时,将模块的所有输入还原使其正常工作[4]。该方法的缺点是需要在运算模块的输入端增加控制逻辑,使其能够在处于冗余状态所有输入信号赋“0”,但同时引入了控制逻辑带来的额外的功耗,影响模块低功耗优化效果。
(3) 存储器分块访问。主要方法是将系统中存储器按照其内部各子模块所需容量进行分块,然后用高位地址线进行片选译码[5]。假设某系统分配到1块128 kB的RAM,其内部2个子模块各自需要1块64 kB的RAM,这时可以选用2块64 kB的RAM和17位的地址线。其中低16位地址线直接提供给2个RAM,最高位地址线接到下面RAM的片选端CS。通过这种方法,不管从CPU 出来的什么样的地址,则每次只会选中1个64 kB的RAM。若采用单块128 kB的RAM,则每次都要选中1块128 kB的RAM,众所周知,1块64 kB RAM的功耗要远小于1块128 kB RAM的功耗。该方法的缺点是需要将地址总线的位宽扩大,同时加入片选逻辑,使系统在降低功耗同时引入了总线扩宽和片选逻辑带来的额外的功耗,影响系统的低功耗优化效果。
本文的目的在于针对上述应用背景以及现有低功耗设计的不足,提出一种针对定点小数乘法运算的低功耗设计算法与实现技术,其优点在于:
(1) 由于该算法从优化乘法器内部加法结构入手,没有引入任何的缺省操作,因此不损失乘法运算精度,而且只是减少了乘法器综合后转化为加法器的数量,不需要降低系统工作时钟频率和工作电压,不会降低系统工作效率。
(2) 由于该算法可以在各级加法结果中,预先计算出将要在最终乘法结果中被缺省的“最小贡献位”,因此可以直接在本级加法结果中缺省来减小本级加法结果的位宽,即在不降低乘法运算速度与运算精度的基础上降低乘法器的功耗和面积。
(3) 由于在运算过程中只需搜索乘法器系数中“1”的排列和位置并加以计算,因此具有运行速度快,占用资源少,简单易行的优点。
(4) 由于该算法采用了一种全新的实现技术,使得综合后只有优化结果参与生成系统门级电路,而优化算法自身的逻辑单元不会引入到系统中。对于含有大规模乘法运算的系统,避免其内部各乘法器引入优化逻辑自身的功耗和面积累加入被优化系统,从而提升优化效果。
1 关于定点二进制小数乘法运算
在二进制数字电路设计中,数据宽度n所能表达出的最大数被归一化为“1”,小数则被表示为所占该“归一化1”的比例,因此,n位的小数B可以被整数化处理为二进制数X [6]:
 (1)
(1)
例如16位小数0.141677856,由式(1)整数化处理为0.141677856/(216-1)=9285(10010001000101b),这里65536(1111,1111,1111,1111b)被归一化为“1”,从数据操作的角度来看,相当于将0.141677856左移16位。这样小数乘法运算就可以暂时转化为整数乘法运算,但乘法结果需要右移16位转化回小数,才能得到最终的小数乘法运算结果。
以16位小数乘法64921×0.141677856为例,依式(1)整数化处理为64921×9285,其乘法竖式如图1所示,整数乘法运算结果为100011111011011101111000111101b,然后右移16位得到小数乘法运算结果10001111101101.1101111000111101b,保留16位的位宽后结果为10001111101101.11b。
小数乘法器内部寄存器的位宽由其输出结果的精度所决定,寄存器位宽的增加是减少整个数据通路的数据损失[7]。如果输入数据的位宽是Bin,则输出数据的最大位宽为Bmax=Nlog2RM+Bin-1的上限整数值[8],其中,N为内部加法运算次数,RM为小数乘法器运算精度。可以看出Bmax会导致很大的位宽,这时就需要对小数乘法器内部各级加法结果作截断和近似处理[9]。当假设输入和误差源都是相互独立的,并且服从均匀分布,则如果设第i级加法结果的截断误差为Ei=2Bi,其中Bi是舍弃的低位,则误差的均值和方差分别为ui=0.5Ei, [10]。舍弃数据低位而不导致降级精确度的主要依据是要让前2N位误差方差的总合小于或者等于最后第2N+1个误差源所产生的误差,其表达式为
[10]。舍弃数据低位而不导致降级精确度的主要依据是要让前2N位误差方差的总合小于或者等于最后第2N+1个误差源所产生的误差,其表达式为
 ,i=1, 2, …, 2n (2)
,i=1, 2, …, 2n (2)
而其中 ,
,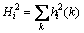 ,
, ,由
,由 ,由此可得其每一级最终舍弃位宽表达式为
,由此可得其每一级最终舍弃位宽表达式为
 (3)
(3)
式中:Bi为不大于右端表达式计算值的最大整数。由式(3)中右端第2项可知:要计算某一级舍弃位宽,首先要计算最后部分舍去的位宽,如果在最后一级输出位宽为Bout,则2N+1级所舍弃的位宽为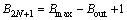 。
。
由图1可见:该乘法运算转化为4次加法运算,且各级加法运算结果的位宽分别为19,23,27和30。若将各级加法结果均保持在16位,即舍弃所有大于16位的数据低位,则乘法运算结果变为1000111110110111b,如图2所示,与图1所示的原结果相比存在相当大的误差。

图1 64921×9285的乘法竖式
Fig. 1 Formula of 64921×9285

图2 保持16位数据宽度的乘法竖式
Fig. 2 Formula of maintain 16-bit data width in each adder
在小数乘法运算中,中间各级加法结果的数据末位会参与下级加法运算,因此为了保持运算结果的准确性,需要完整保留中间各级加法结果,只能在最末级加法结果中进行缺省来满足小数乘法位宽要求,否则会出现较大的误差累积[11]。若能在各级加法结果中预先计算出会在最末级加法结果中被缺省掉的数据末位,进而在各级加法结果中提前缺省,则可以有效减少各级加法结果位宽,同时保证最终运算结果的准确性。
2 数据宽度的优化
整数乘法运算A×B的计算过程如式(4)所示[12],其中被乘数和乘数分别为A和B,B以二进制表示为b3b2b1b0。

 (4)
(4)
提出系数b0后,式(4)可转化为
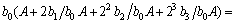
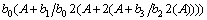 (5)
(5)
由式(5)可得:若b0为“0”,则bi2iA项也为“0”。因此对于每一项,其分母必为“1”,否则整个项均为“0”。由此可得多项式:
 (6)
(6)
其等价多项式为:
 (7)
(7)
由式(7)可以看出:本级加法结果的末位不参与下级加法运算,依然作为下级加法结果的末位存在。如果能够缺省本级加法结果的最末i位(i等于下级加法运算中另一个加数的左移位数),则可以减少下级加法结果的位宽,而缺省掉的也只是“最小贡献位”(The last-significant-bits),这些“最小贡献位”也会在最终运算结果中被缺省掉。
对图1乘法竖式依式(7)进行优化,缺省各级加法结果的“最小贡献位”后的乘法竖式如图3所示,末级加法结果为10001111101101110b,由于在优化过程中共缺省 位,因此,仅需对以上结果右移3位即可得出小数乘法结果,并保留16位数据宽度为10001111101101.11b,与优化前完全一致。但注意到优化后各级加法结果位宽分别变为17,17,17和17,相比较优化前的位宽19,23,27和30,可以计算出在乘法运算64921×9285内部共节省寄存器位宽
位,因此,仅需对以上结果右移3位即可得出小数乘法结果,并保留16位数据宽度为10001111101101.11b,与优化前完全一致。但注意到优化后各级加法结果位宽分别变为17,17,17和17,相比较优化前的位宽19,23,27和30,可以计算出在乘法运算64921×9285内部共节省寄存器位宽 位,同时优化没有带来额外误差,没有降低乘法运算准确度。
位,同时优化没有带来额外误差,没有降低乘法运算准确度。

图3 缺省优化过程
Fig. 3 Omit operation process
3 乘法系数的优化
对于二进制乘法运算,普遍采用移位加算法,即每一个部分积都是由被乘数与乘数中各位相乘产生,然后按照加法运算规则将各部分积相加[13]。以8位二进制乘法运算111011b×1110111b为例,其乘法竖式如图4所示,其乘法结构框图如图5所示,其中x为被乘数。

图4 111011b×1110111b的乘法竖式
Fig. 4 Formula of 111011b×1110111b

图5 乘法器内部结构框图(系数为1110111b)
Fig. 5 Multiplier structure schematic (the coefficient is 1110111b)
观察发现乘法运算内部移位加运算的次数m与乘数中“1”的个数n密切相关,如图4中乘法运算转化为5次移位加运算,而乘数1110111b含有6个“1”,它们的关系满足 。因此如果能够设法减少乘数中“1”的个数,则同一乘法器中所含的加法器个数就会减少,该乘法器的功耗和面积也会随之降低[14]。
。因此如果能够设法减少乘数中“1”的个数,则同一乘法器中所含的加法器个数就会减少,该乘法器的功耗和面积也会随之降低[14]。
对于任意二进制数X,对其中连续“1”取补码后,记为 ,如式(8)所示[15],其中
,如式(8)所示[15],其中 和
和 分别为补码中“1”的最高位和最低位,此时该二进制数中不存在连续的“1”,即
分别为补码中“1”的最高位和最低位,此时该二进制数中不存在连续的“1”,即 。
。
 (8)
(8)
 由式(9)得出,其中
由式(9)得出,其中 为该二进制数。
为该二进制数。
 (9)
(9)
结合式(8)和式(9),若对乘法系数中连续的“1”取补码,则对于给定的系数长度L和M位的补码为
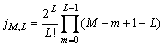 (10)
(10)
当L未约束时, ,
, (其中,K为补码长度);一旦Lmax确定,Kc由式(11)得出。
(其中,K为补码长度);一旦Lmax确定,Kc由式(11)得出。
 (11)
(11)
例如,二进制数1110111b的补码计算过程如图6所示。

图6 二进制数1110111b的补码计算过程
Fig. 6 Complement calculation process of binary 1110111
基于优化后系数 ,新的乘法竖式如图7所示,新的乘法结构框图如图8所示。与优化前的乘法运算相比,它们得出相同的运算结果1101101101101b,但移位加运算由5次减少为2次。可以看出该优化对于减少乘法器中加法运算次数效果显著,同时不影响运算结果与精度。
,新的乘法竖式如图7所示,新的乘法结构框图如图8所示。与优化前的乘法运算相比,它们得出相同的运算结果1101101101101b,但移位加运算由5次减少为2次。可以看出该优化对于减少乘法器中加法运算次数效果显著,同时不影响运算结果与精度。

图7 优化后的二进制乘法竖式
Fig. 7 Optimized binary multiplication formula

图8 优化后的乘法器内部结构框图
Fig. 8 Structure schematic of optimized multiplier
4 优化算法的实现技术
针对现阶段低功耗设计中存在的问题,即优化后的系统往往会引入一部分低功耗算法自身的功耗和面积,它们会累加入优化后的系统从而抵消系统整体优化效果。为了解决该问题,本文开发出一种新的算法实现技术,它可以避免优化算法自身逻辑单元进入优化后的乘法器,进一步提升其低功耗效果。
对于小数乘法器,先将系数按式(1)整数化处理后,对整数系数X由最低位向高位搜索,逢“1”则记录其位置和符号,分别以变量 和
和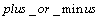 表示,即x(i)=1
表示,即x(i)=1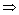 position_of_1(i)=1,
position_of_1(i)=1, ,同时“1”的总数加1,以变量
,同时“1”的总数加1,以变量 表示,即
表示,即 ;逢“0”则判断之前有没有连续的“1”存在,若有,则这些连续“1”按照前面所述算法进行转化,然后,更新上述3个参数:
;逢“0”则判断之前有没有连续的“1”存在,若有,则这些连续“1”按照前面所述算法进行转化,然后,更新上述3个参数: ,
, 和
和 ;若无,则继续向高位搜索。按上述算法搜索至X最高位,整数系数X的优化结束。依此算法对乘法器系数1110111b(如图6所示)进行优化后的仿真波形如图9所示,仿真工具为Mentor Graphic公司的modelsim,优化结果为:total_1=3, position_of_1=730, plus_or_minus=100。即优化后的系数中总共有3个“1”,它们的位置分别在第0位、第3位、第7位,它们的符号分别为+、-、-,即
;若无,则继续向高位搜索。按上述算法搜索至X最高位,整数系数X的优化结束。依此算法对乘法器系数1110111b(如图6所示)进行优化后的仿真波形如图9所示,仿真工具为Mentor Graphic公司的modelsim,优化结果为:total_1=3, position_of_1=730, plus_or_minus=100。即优化后的系数中总共有3个“1”,它们的位置分别在第0位、第3位、第7位,它们的符号分别为+、-、-,即 ,与前面的理论推算结果一致。
,与前面的理论推算结果一致。

图9 1110111b的优化仿真波形
Fig. 9 Simulation waveform of optimized 1110111b
将以上整数化处理及优化算法实现为一个函数find_multi_factor_f(x),并放入库中与被优化对象分离。优化时只需调用该函数,函数的输入x为乘法器的小数系数,输出为优化后的系数,以3个常数表示:
Constant mum_to_add_c:integer:=find_multi_factor_f(x). otal_1;
Constant shift_bits_c:nature_array:=find_multi_factor_ f(x).position_of_1
Constant add_sign_c:std+ulogic_vector:=find_multi_ factor_f(x).plus_or_minus
这里优化结果以常数表示的原因在于:
(1) 在乘法器综合初期,以上3个常数会根据优化函数find_multi_factor_f(x)计算得出。综合后,乘法器仅仅根据这些常数便可转化为对应的移位加结构,而库中的优化算法逻辑单元不会引入乘法器。
(2) 优化结果中的常数shift_bits_c (优化后系数中各“1”的位置)恰好可以为进一步的针对各级加法结果位宽的优化算法所利用,省掉后者搜索过程,加快计算速度。
设计优化乘法器模块mtplr_mutiplication,其类属参数为multi_find_g、输入端口为西x_i与n,输出端口为z_o。其中小数乘法器系数由模块类属参数multi_find_g输入,被乘数由x_i输入,数据宽度由n输入,最终乘法运算结果由z_o输出。图10所示为该优化乘法器模块的实体。
在模块内部,调用优化函数find_multi_factor_f(x),并使小数乘法器系数通过类属参数multi_find_g输入优化函数,输出结果为3个常数:num_to_add_c,shift_bits_c和add_sign_c,其与被乘数构建移位加法运算。

图10 mtplr_mutiplication的实体
Fig. 10 Entity of mtplr_mutiplication
由于优化后系数中“1”的位置已经在常数阵列shift_bits_c中保存,分别记为n1, n2, …, nk。因此,综合后第一个加法器是由被乘数A左移n1位加A左移n2位构成,并缺省加法结果的最末n2位存入寄存器作为第一个中间结果A1;第i个加法器是由A左移ni位加前一个中间结果Ai-1构成,并缺省加法结果的最末ni位存入寄存器作为第i个中间结果Ai,依此类推,直到构建出k-1个加法器。优化算法流图如图11所示。
最后需要对最末级加法结果进行小数化处理。由于开始先对n位小数乘法器A×B中小数系数B进行了整数化处理,相当于将B左移n位,因此最末级加法结果需要右移n位转化回小数后得到最终乘法结果。然而在“缺省”过程中最大缺省位为nk,即在优化过程中已经右移了nk位,所以最后一级加法器的结果只需右移n-nk位并由z_o输出。
对含有大量小数乘法器的系统进行优化时,将优化乘法器模块mtplr_mutiplication置于库中与系统设计分离,在系统中实例化该模块并替换掉原有各定系数乘法器,替换时将各实例化模块的类属参数设定为所对应乘法器系数。
系统设计的参数和特性一旦确定,其内部各乘法器系数也将确定。以FIR滤波器为例,一旦阶数、通带带宽、截止频率等参数确定,其内部各乘法器的系数也将确定。乘法器系数由类属参数传入而不以常数传入的原因是:常数只能从设计实体的内部得到赋值且不能再改变,而类属的值可以由设计实体外部提供,因此设计者可以从外面通过类属参量的重新设定而容易地改变该模块的内部电路结构,即在替换时只需将各乘法系数通过类属参量传入模块便可实现不同的优化乘法器,图12所示为替换16位小数乘法y=0.141677856x的优化乘法器的优化乘法器模块。前面所例举的16位定点小数乘法运算64921×0.141677856的优化仿真波形如图13所示,其中乘法系数multi_find_g为0.141677856;被乘数x_i为 64921;位宽n为16,乘法器内部4个加法运算结果A1,A2,A3和A4分别为10011110011111111b,10001000101101000b,10000111010101111b和10001111101101110b,最终16位运算结果z_o为9197.75,即10001111101101.11b,与图3中的理论运算结果一致。

图11 小数乘法器优化设计算法流图
Fig.11 Optimization methodology schematic of decimal multiplier

图12 替换16位小数乘法y=0.141677856x的优化乘法器模块
Fig. 12 Optimized multiplication module that is instead of 16-bit decimal multiplier y=0.141677856x
在综合初期,乘法器的系数通过模块类属参数multi_find_g传入优化函数中,得到以3个常数表示的优化系数。综合时根据这些常数,乘法器就可以转化为对应的移位加法器,同时根据记录优化后系数中“1”位置的常数shift_bits_c,针对各级加法结果缺省掉对计算精度无任何贡献的数据末位,从而减少各级加法结果位宽。这时库中的优化逻辑单元自身不会进入系统综合后的门级电路中,而模块内部只含有缺省操作,未增加额外的逻辑运算。

图13 小数乘法64921×0.141677856的优化仿真波形
Fig.13 Simulation waveform of optimized decimal multiplication 64921×0.141677856
5 优化效果验证
为了测试优化效果,以某含有大量数字滤波器和数字信号处理的射频模块作为测试对象,对其进行优化。该射频模块具备语音信号调制及发射功能,其内部含有梳状滤波器、WDF滤波器等不同类型的数字滤波器,以及信号处理器等含有大量小数乘法运算的子模块。
优化结果的测试工具为Sequence Design公司的 Power Theater,作为标准功耗计算工具,它可以对系统的前端RTL代码计算出准确的功耗和面积。分别用该工具对优化前的射频模块,经本文所述优化算法匹配一般实现技术优化过的射频模块,以及本文所述优化算法匹配本文所述实现技术优化过的射频模块分别进行测试,3次测试中对射频模块的工作电压,工作时钟频率等所有输入参数均保持一致。表1记录了3次测试所得的功耗测试结果,表2记录了3次实验所得的面积与逻辑单元数。可以看出:优化前模块的功耗为10.7 mW,逻辑单元数为95 962,面积为1.479 mm2;经本文所述优化算法匹配一般实现技术优化后,以上参数分别为6.903 mW,70 220和1.147 mm2,分别降低35.51%,7.06%和22.45%,优化结果证明本文所述算法具有较好的低功耗效果;完全按照本文所述低功耗算法优化后,以上参数分别为6.31 mW、67 888和1.119 mm2,分别再次降低8.55%,3.32%和2.44%,说明本文所述实现技术确实可以提升系统整体低功耗效果,解决了目前低功耗设计所存在的问题。
为了进一步测试本文所述低功耗算法的硬件优化效果,分别对优化前的射频模块和经一般低功耗算法优化后的射频模块以及本文所述低功耗算法优化过的射频模块进行FPGA测试。测试采用Stratix Ⅳ家族EP4SE820F43C3型号FPGA作为测试平台,并且采用QuartusⅡ作为FPGA的编译、综合工具,该工具来自于ATERA公司,并且作为业内普遍认可的一种FPGA开发工具。优化前模块与一般实现技术以及本文所述实现技术优化后的模块经QuartusⅡ编译、综合后由其产生的资源报告对比如表3所示。由表3可见:该报告准确记录了3次测试中测试对象对于该型号FPGA的资源占用情况。可以看出优化前射频模块对该FPGA的逻辑占用率为5.6%,生成寄存器总数为18 175,存储单元占用率为6.5%;经本文所述优化算法匹配一般实现技术优化过的射频模块对该FPGA的逻辑占用率为3.7%,生成寄存器总数为11 558,存储单元占用率为4.2%,分别降低33.93%,36.41%和35.38%;经本文所述优化算法匹配本文所述实现技术优化后,该射频模块对该FPGA的逻辑占用率为3.4%,生成寄存器总数为10 001,存储单元占用率为4.1%,分别再次降低8.11%,13.47%和2.38%。FPGA测试结果对比明显,而且与Power Theater所取得的功耗分析结果相吻合。这是由于经一般实现技术优化后,虽然各乘法器的结构和位宽得以优化,但优化算法逻辑单元同时也被引入到各乘法器中,增加了一些逻辑单元和面积,这抵消掉了一部分整体优化效果;而经本文所述实现技术优化后,乘法器的结构和位宽同样得到优化,而且避免了优化算法逻辑单元引入到各乘法器中,即避免了优化设计所带来的副作用。这是2种实现技术所得测试结果相差很大的主要原因。
表1 3次实验所得的射频模块各项功耗
Table 1 Power analysis record of RF module in 3 experiments mW

表2 3次实验所得的射频模块逻辑单元数和面积
Table 2 Logic cell number and area of RF module in 3 experiments

表3 FPGA测试结果对比
Table 3 FPGA test result comparison

6 与综合工具自动优化结果的对比
在硬件开发流程中的综合阶段,一些综合工具中自带的IP核能够以某些规则对被综合对象进行相应的自动优化,例如面积、功耗等。为了对比本文所述低功耗算法与综合工具自动优化功能的效果,以Synopsys公司的DC(Design Compiler)对未经优化的原始射频模块进行综合,DC作为业内广泛认可的逻辑综合工具,它可以根据设计描述和约束条件自动综合出优化后的门级电路,提高硬件设计性能。
首先在DC的约束文件synopsys_dc.setup中设置面积最小化,这里需要指出的是,DC中的约束文件中可以牺牲某一方面的性能来改变其他方面的性能,其中最直接的就是面积与延时的权衡,因此为了使综合后射频模块的面积与功耗能够达到最小,synopsys_dc.setup中没有对延时做出任何约束,意味着在此约束条件下射频模块的面积与功耗最小,而关键路径的延时可能相当大。但这样做的目的是以DC能够达到的最小面积和最低功耗与本文所述算法和实现技术所取得的结果进行对比。
综合完成后,得到的各项功耗结果如表4所示,面积结果如表5所示,为了便于对比,将表1和表2中本文所述优化技术优化后的测试结果引入。可以看出:同一射频模块经DC在面积最小的约束条件下综合后,模块的总功耗降为8.84 mW,面积降为1.357 mm2;而经本文所述优化技术优化后,以上参数分别降为6.325 mW和1.119 mm2,由此可以得出本文所述优化技术所取得的低功耗效果优于综合工具DC能够达到的最优结果。
表4 射频模块的各项功耗对比
Table 4 Power consumption comparison of RF module mW

表5 射频模块综合后的面积对比
Table 5 Area comparison of RF module mm2

7 结论
(1) 对射频模块的功耗分析和FPGA测试结果均表明,本文提出的低功耗算法对含有大量小数乘法运算的系统的优化效果十分显著。
(2) 在算法的实现技术上,解决了目前低功耗设计中算法自身的逻辑单元被引入系统从而降低系统优化效果的问题,并且与现阶段一般实现技术相比较,功耗分析和FPGA测试结果均表明本文所述实现技术的优化效果优于现阶段一般实现技术的结果。
(3) 与业内广泛认可的逻辑综合工具DC自动优化的结果相比,本文提出的低功耗技术具有更优的低功耗效果。
(4) 目前以该低功耗技术对某一通信芯片优化后,芯片已基于65 nm级工艺投片,芯片测试结果良好。
参考文献:
[1] 邓军, 杨银堂. 全数字接收机中一种低功耗插值滤波器结构及其VLSI实现[J]. 西安电子科技大学学报,2010,37(2):320-325.
DENG Jun, YANG Yintang. The VLSI implementation of a low-power interpolation filter structure in all-digital receiver[J]. Journal of Xidian University, 2010, 37(2): 320-325.
[2] 王斌, 吴伟仁, 曲毓萱, 等. 一种用于UWB接收端的带通滤波器分析与设计[J]. 中南大学学报(自然科学版), 2012, 43(2): 554-560.
WANG Bin, WU Weiren, QU Yuxuan, et al. Analysis and design of a band-pass filter for UWB receiver[J]. Journal of Central South University (Science and Technology), 2012, 43(2): 554-560.
[3] 蒋俊正, 王小龙, 水鹏朗. 一种设计DFT调制滤波器组的新算法[J]. 西安电子科技大学学报,2010,37(4):689-693.
JIANG Junzheng, WANG Xiaolong, SHUI Penglang. A new algorithm of DFT modulated filter[J]. Journal of Xidian University, 2010, 37(4): 689-693.
[4] Kodi A K, Sarathy A, Louri A, et al. Adaptive inter-router links for low-power, area-efficient and reliable Network-on-Chip (NoC) architectures[C]// ASP2DAC 2009. Athens: Ohio Univ, 2009: 1-126.
[5] Kodi A K, Louri A, Wang J M. Design of energy-efficient channel buffers with router bypassing for network-on-chips (NoCs)[C]// 10th International Symposium on Quality of Electronic Design. San Jose, CA, USA, 2009: 826-832
[6] Wong A C W, Kathiresan G, Chan C K T, et al. A1V wireless transceiver for an ultra low power SoC for biotelemetry applications[C]// European Solid State Circuits Conf. Abingdon: Toumaz Technol Ltd, 2007: 127-130.
[7] Priest D M. Algorithms for arbitrary precision floating point arithmetic[C]// 10th IEEE Symposium on Computer Arithmetic. Los Alamitos, CA, USA. 1991: 132-144.
[8] 罗柏文, 万明康, 于宏毅. 两种基于自适应相位补偿的FDOA估计算法[J]. 数据采集与处理, 2012, 27(1): 538-545.
LUO Baiwen, WAN Kangming, YU Hongyi. Two kinds of estimation algorithm based on adaptive phase compensation FDOA[J]. Journal of Data Acquisition and Processing, 2012, 27(1): 538-545.
[9] Daniele L, Macro R. Binary canonic signed digit multiplier for high-speed digital signal processing[C]// The 47th IEEE International Midwest Symposium on Circuits and Systems. Hiroshima, Japan, 2004: 205-208.
[10] Hartley R I. Subexpression sharing in filters using canonic signed digit multipliers[C]// IEEE Transactions on Circuits and Systems Ⅱ. Analog and Digital Signal Processing. Schenectady, NY, 1996: 52-54.
[11] Graillat S, Langlois P, Louvet N. Compensated Horner scheme[R]. Perpignan, France: University of Perpignan, 2005: 10-26.
[12] Losada R A, Lyons R. Reducing CIC filter complexity[M]. Natick, MA, USA: IEEE Signal Processing Magazine MathWorks Inc., 2006: 124-126
[13] Meyer-Baese U. Digital signal processing with field programmable gate arrays[M]. New York: Springer Publishing Company, 2007: 539-790.
[14] Karlsson M. Implementation of digital serial filters[R]. Sweden: Link ping Studies in Science and Technology Dissertations, 2005: 925-1102.
ping Studies in Science and Technology Dissertations, 2005: 925-1102.
[15] Lyons R G. Understanding digital signal processing[M]. Upper Saddle River, New Jersey: Prentice Hall, 2004: 556-561.
(编辑 杨幼平)
收稿日期:2012-12-11;修回日期:2013-03-06
基金项目:国家自然科学基金资助项目(60976068);教育部科技创新工程重大项目培育资金资助项目(708083);教育部博士点基金资助项目(200807010010)
通信作者:袁博(1982-),男,陕西西安人,博士研究生,从事大规模集成电路设计研究;电话: 13991300901;E-mail: wison_yuan@hotmail.com
摘要:针对集成电路前端设计中的定点小数乘法器,提出一种既能够优化其内部加法器数量又能优化各级加法结果位宽的低功耗算法,而且在算法的实现技术上,解决目前低功耗设计中算法自身逻辑单元引入被优化系统从而降低系统优化效果的问题。在介绍该算法的理论基础和实现细节后,为了取得更加客观、更具有统计特性的低功耗优化效果,以该算法对某含有大量不同类型小数乘法器的射频模块进行优化。优化后FPGA测试结果显示逻辑占用率降低了39.3%,寄存器总数降低了45.0%,内存占用率降低了36.9%。该算法是一种高效的低功耗算法,并且解决了一般算法实现技术的缺陷与不足,其适用于对含有大量小数乘法运算的系统进行低功耗优化,例如数字信号处理和数字滤波器等。
[1] 邓军, 杨银堂. 全数字接收机中一种低功耗插值滤波器结构及其VLSI实现[J]. 西安电子科技大学学报,2010,37(2):320-325.
[2] 王斌, 吴伟仁, 曲毓萱, 等. 一种用于UWB接收端的带通滤波器分析与设计[J]. 中南大学学报(自然科学版), 2012, 43(2): 554-560.
[3] 蒋俊正, 王小龙, 水鹏朗. 一种设计DFT调制滤波器组的新算法[J]. 西安电子科技大学学报,2010,37(4):689-693.
[8] 罗柏文, 万明康, 于宏毅. 两种基于自适应相位补偿的FDOA估计算法[J]. 数据采集与处理, 2012, 27(1): 538-545.


