随时间任意变化荷载下砂井地基固结分析
郭彪1,2,韩颖3,龚晓南2,卢萌盟4
(1. 重庆市市政设计研究院,重庆,400020;
2. 浙江大学 软弱土与环境土工教育部重点实验室,浙江 杭州,310058;
3. 机械工业第三设计研究院,重庆,400039;
4. 中国矿业大学 深部岩土力学与地下工程国家重点实验室,江苏 徐州,221008)
摘 要:
化的荷载作用下砂井地基固结问题进行研究。首先推导考虑涂抹效应、井阻作用、土体内径竖向组合渗流、变荷载以及涂抹区水平渗透系数线性连续变化等因素的解析解;然后,将上部荷载进行傅里叶变换转化为三角级数的形式,即将复杂荷载分解为很多简单的正余弦函数之和,通过简单荷载作用下响应的叠加得到原复杂荷载作用下的响应,由此得到一种便于工程应用的简单方法;编制计算程序,与传统解析解进行对比;最后,分析几种荷载模式下砂井地基的固结性状,包括多级线性加载、三角形循环荷载、矩形循环荷载等一般模式,并通过用多段直线段逼近曲线的方法,分析抛物线形循环荷载作用下地基的固结特性。研究结果表明:本文方法合理,具有广泛的适用性。
关键词:
中图分类号:TU41 文献标志码:A 文章编号:1672-7207(2012)06-2369-09
Consolidation analysis with vertical drains and general time-dependent loading
GUO Biao1,2, HAN Ying3, GONG Xiao-nan2, LU Meng-meng4
(1. Chongqing Municipal Institute of Design, Chongqing 400020, China;
2. Key Laboratory of Soft Soils and Geoenvironmental Engineering,
Zhejiang University, Hangzhou 310058, China;
3. China Third Design Institute Engineering Corporation, Chongqing 400039, China;
4. State Key Laboratory for Geomechanics and Deep Underground Engineering,
China University of Mining & Technology, Xuzhou 221008, China)
Abstract: The consolidation behavior of soils with vertical drains subjected to a general time-dependent loading was studied. Firstly, an analytical solution was obtained accounting for the effects of soil smear, drain hydraulic resistance, coupled flows in the radial and vertical directions within the surrounding soil, time-dependent loading and the linear distribution of the horizontal permeability of soils in the disturbed soils zone. Then, the time-dependent loading was transferred to trigonometric series by the technique of Fourier Transform. By this method, the complex loading was transformed into the sum of a series of sine and cosine function. Then the response of the complex loading was obtained by superimposing the responses of these relatively simple ones. A simple-to-use method was proposed according to this method. Consequently, a calculation computer program was developed and the comparison with a theoretical method was made. Finally, the consolidation behavior of sand drains foundation under several conventional types of time-dependent loading was investigated, including multi-ramp loading, triangular cyclic loading and trapezium cyclic loading. Moreover, the consolidation behavior of sand drains foundation under parabolic cyclic loading was investigated by means of piecewise-linear approximation method. The results indicate that the proposed method is accurate and reasonable.
Key words: consolidation; vertical drains; time-dependent loading; Fourier transform
砂井联合堆载预压是提高软土地基承载力、减小地基沉降的有效方法,对常荷载下砂井地基的固结问题,国内外众多学者进行了大量的研究,取得了丰富的成果[1-16]。但在实际工程中,地基荷载通常是随时间变化的,对于变荷载下的砂井地基固结问题,也有不少研究者进行了研究,如:Olson[16]假设砂井为理想井,给出了荷载分级线性施加情况下的解析解;Tang 等[17-18]进一步考虑了涂抹和井阻作用;Zhu等[19]用数值方法对砂井地基进行了研究,并考虑了大变形、非线性等因素的影响;耿雪玉等[20]运用Laplace变换求得了复杂荷载作用下未打穿砂井地基的固结解。上述解答要么考虑的因素不够全面,要么过于复杂,很难应用于工程实践。另外,大量的研究[12-14]表明:涂抹区土体由于受到的施工扰动程度不同,其渗透性是连续变化的,离砂井越近,扰动程度越高,土的渗透性越小。为此,本文作者考虑涂抹效应、井阻作用、地基土横竖向组合渗流等因素,并且涂抹区的水平渗透系数采用更符合实际的线性连续变化模式,将上部荷载通过傅里叶变换转化为三角级数的形式[21],得到更便于工程应用的分析变荷载下砂井地基固结的解析解,并编制了应用程序。
1 固结方程及求解
图1所示为随时间任意变化荷载下砂井地基示意图。在推导过程中,进行以下假定:
① 等应变条件成立;
② 土中水的渗流服从Darcy定律;
③ 荷载在地基中引起的附加应力沿深度均匀分布;
④ 在任一深度z处从土体流入桩体的水量等于桩体中向上水流的增量。
根据等应变条件,有:
![]() (1)
(1)
式中:εv为地基竖向应变;Es为土体压缩模量;q(t)为上部荷载;![]() 为土体任一深度处的平均超静孔压,
为土体任一深度处的平均超静孔压,
![]() (2)
(2)
rw为砂井半径;re为砂井影响区半径;u为土体任一点的超静孔压。
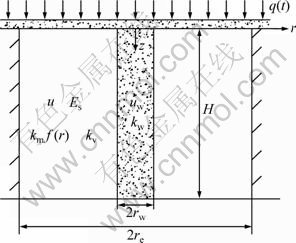
图1 随时间任意变化荷载下砂井地基简化模型
Fig.1 Model for consolidation of soft soil with vertical drains and general time-dependent loading
根据谢康和等[9]的研究,砂井地基的固结方程为:
![]() (3)
(3)
式中:kv为土体竖向渗透系数;kw为砂井渗透系数;kmf(r)为土体水平向渗透系数;km为最大水平渗透系数;f(r)为描述渗透系数随![]() 变化的函数。桩周流量连续方程为:
变化的函数。桩周流量连续方程为:
![]() (4)
(4)
式中:uw为砂井任一深度处的超静孔压。边界条件为:
(1) r=re时,![]() ;
;
(2) r=rw时,u=uw;
(3) z=0时,![]() =0,uw=0;
=0,uw=0;
(4) z=H时,![]() 。
。
任何加载都需要一个过程,即使是瞬时加载也是如此,只不过时间很短。因此,初始条件可写为:
⑤ t=0时,![]() =0。
=0。
参考文献[10,17],可以得到固结控制方程为:
![]() (5)
(5)
![]() (6)
(6)
式中:
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
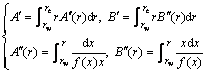 (11)
(11)
![]() ;
;![]() ;土体竖向固结系数
;土体竖向固结系数![]() 。
。
假设地基土体涂抹区水平渗透系数随![]() 增大而线性增大,未扰动区保持不变,不妨称其为模式1,如图2(a)所示。参考文献[10],可以得到:
增大而线性增大,未扰动区保持不变,不妨称其为模式1,如图2(a)所示。参考文献[10],可以得到:
![]() (12)
(12)
其中:
![]()
![]()
![]()
![]()
![]() (13)
(13)
s=rs/rw;rs为涂抹区半径;δ为最小渗透系数和最大渗透系数之比,0<δ=kn/km<1。
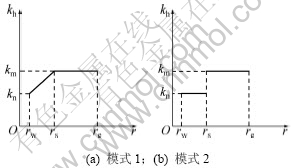
图2 影响区土体水平渗透系数
Fig.2 Horizontal permeability coefficient in influence zone
为了便于比较分析,本文也给出涂抹区水平渗透系数不变情况下(模式2)的解,如图2(b)所示。此时,Fa的表达式为:
![]()
![]() (14)
(14)
方程(5)是非齐次微分方程,其边界条件式③和④以及初始条件式⑤是齐次的,满足冲量定理条件,可设:
![]() (15)
(15)
![]() (16)
(16)
由式(6),![]() 和
和![]() 满足关系式:
满足关系式:
![]() (17)
(17)
其中,![]() 方程(5)对应齐次微分方程的解:
方程(5)对应齐次微分方程的解:
![]() (18)
(18)
边界条件和初始条件为:
⑥ z=0时,![]() ;
;
⑦ z=H时,![]() ;
;
⑧ t=τ+0时,![]() 。
。
采用分离变量法求解,设
![]() (19)
(19)
代入式(18)可得:
![]() (20)
(20)
即
![]() (21)
(21)
![]() (22)
(22)
利用边界条件⑥和⑦以及式(17)和(19),可得:
⑨ z=0时,![]() ;
;
⑩ z=H时,![]() 。
。
常微分方程(21)的特征方程为:
![]() (23)
(23)
其解可表示为:
![]() (24)
(24)
![]() 有一正一负2个值。可设式(23)的根为±λi,±ξ,其中λ>0,ξ>0。
有一正一负2个值。可设式(23)的根为±λi,±ξ,其中λ>0,ξ>0。
式(21)的通解可表示为:
![]()
![]() (25)
(25)
由边界条件⑧和⑨可得:
b=c=d=0
则![]() 。由z=H和Z′(z)=0可得:
。由z=H和Z′(z)=0可得:
sin(λH)=0(a≠0),否则解为0。则![]() ,
,![]() ;m=1,2,3…。
;m=1,2,3…。
将k=λi代入式(23),可得:
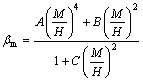 (26)
(26)
方程(22)的通解可表示为:
![]() (27)
(27)
由于其初始时刻为t=τ+0,可设![]() ,Δ为1个常数,则:
,Δ为1个常数,则:
![]() (28)
(28)
方程(18)的解可写成:
![]() (29)
(29)
将式(29)代入式(17)可得:
![]() (30)
(30)
根据三角函数的正交性和初始条件⑧可得:
![]() (31)
(31)
将式(29)和(30)分别代入式(15)和(16)可得固结方程的解为:
![]() (32)
(32)
![]() (33)
(33)
在q(t)比较复杂的情况下,上面的解难以应用,为方便工程应用,需要将其简化。对荷载q(t),一般来说是满足狄利克雷(Dirichlet)条件的,可将其展开成傅里叶级数:
![]()
![]() (34)
(34)
![]() (35)
(35)
![]() (36)
(36)
![]() (37)
(37)
![]() (38)
(38)
![]() (39)
(39)
式中:![]() ;T为q(t)的周期。在q0的作用下,dq0=dt=0,因此,对地基孔压没有影响。
;T为q(t)的周期。在q0的作用下,dq0=dt=0,因此,对地基孔压没有影响。
在变载qn(t)作用下,将式(39)代入式(32)和(33)并积分可以得到:
![]()
![]()
![]() (40)
(40)
![]()
![]()
![]() (41)
(41)
运用叠加原理,地基在荷载q(t)作用下,砂井和地基土的平均超静孔压可写成:
![]() (42)
(42)
![]() (43)
(43)
求得了![]() 后,可以得到地基任意深处的固结度为:
后,可以得到地基任意深处的固结度为:
![]() (44)
(44)
式中:qu为最大荷载。
进一步可以得到地基的总平均估计度为:
![]() (45)
(45)
式中:
![]()
![]()
![]() (46)
(46)
2 an和bn的求解
系数an和bn的求得是上述求解过程中的关键。在分级线性施加荷载情况下(如图3所示),对其中任意一级加载,q(t)可写为:
![]() (47)
(47)
将式(47)代入式(36)和(37)可以得到:
![]() (48)
(48)
![]() (49)
(49)
其中:
![]()
![]()
![]() (50)
(50)
![]()
![]()
![]() (51)
(51)
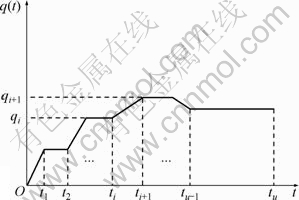
图3 分级线性施加荷载示意图
Fig.3 Loading process consisting of a combination of linear and constant functions with time
在荷载随时间曲线变化的情况下,可以用直线段来模拟,如图4所示。当直线段足够多时,就可以达到足够工程应用的精度要求。这样,可以同样采用式(48)~(51)求得an和bn。
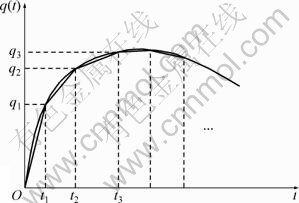
图4 荷载随时间曲线变化示意图
Fig.4 Relationship between loading and time
3 程序的编制
利用计算机编程,上面的求解过程很容易实现。步骤如下。
(1) 输入地基土参数和砂井参数,包括:砂井半径rw,影响区半径re,涂抹区半径rs,土层厚度H,砂井渗透系数kw,土体竖向渗透系数kv,未扰动土水平渗透系数km,扰动程序参数δ,土体压缩模量Es等。
(2) 输入上部荷载参数,若q(t)由如图3所示的一系列直线段组合而成,则输入各拐点处的时间ti和qi;若荷载为如图4所示的随时间曲线变化,则根据需要取一系列t,再由荷载函数q(t)计算对应的q,时间间隔越小,精度便越高;输入q(t)的周期T,若q(t)不是周期函数,则可将最大分析时间取作T。
(3) 由式(26)求得βm。
(4) 利用式(48),(49)和(50)求得一组系数an和bn。
(5) 利用式(40)和(41)求得在荷载qn(t)作用下砂井和地基土的超静孔压uwn(z,t)和![]() 。
。
(6) 递增n,重复步骤(4)和(5),将其结果叠加求得在荷载q(t)作用下砂井和地基土的超静孔压uw(z,t)和![]() 。
。
(7) 利用式(45)求得地基的平均固结度。
4 解的验证
设荷载单级线性施加,如图5所示。图6所示为本文解与唐晓武解[17]的比较结果。由于唐晓武解假设涂抹区水平渗透系数不变,为了使两者条件一致,本例解中采用式(14)表达的Fa,即模式2。
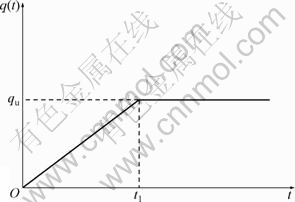
图5 单级线性施加荷载
Fig.5 Single ramp loading
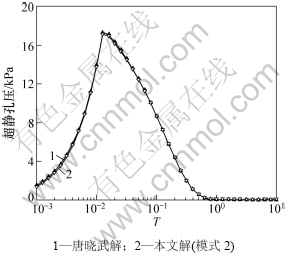
图6 本文解与唐晓武解的比较
Fig.6 Comparison of the present solution with that by Tang X W
由图6可见:2孔压曲线基本上重合,由此可知本文解是可靠的。计算参数为:wr=0.2 m,re=4 m,rs=2 m,H=20 m,kw=1×10-3 cm/s,km=kv=1×10-6 cm/s,δ=0.5,Es=20 MPa,达到最大荷载时间t1=30 d,最终荷载qu=20 kN。
5 几种荷载形式下的固结性状
5.1 多级线性施加荷载
荷载分级线性施加示意图如图7所示。其中,荷载分两级线性施加,t1=30 d,t2=60 d,t3=100 d,q1=20 kN,qu=50 kN。其他计算参数与上例的相同。2种渗透系数模式下超静孔压曲线及固结曲线如图8和图9所示。从图8和图9可以看出:考虑渗透系数呈线性变化时固结要快。
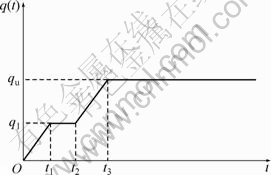
图7 荷载分级线性施加示意图
Fig.7 Multi-ramp loading
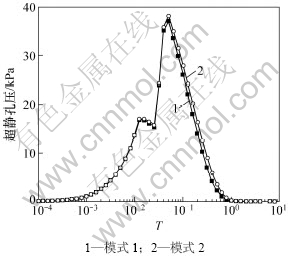
图8 荷载两级线性施加时地基的超静孔压曲线
Fig.8 Excess pore-water pressure of sand drains foundation under double-ramp loading
5.2 三角形循环荷载
三角形循环荷载如图10所示,其中T=60 d,qu=50 kPa,其他计算参数与前面的相同。地基超静孔压变化曲线如图11所示。从图11可以看出:超静孔压呈震荡减小趋势,震荡幅度并不随时间减小,但其震荡中线逐渐趋于一定值;在循环荷载作用下,当上部荷载减小即卸荷时,地基土回弹体积膨胀,从而产生负超静孔压。渗透系数为模式1时的孔压曲线在模式2时孔压曲线的下方,即孔压为正时,模式1的孔压小于模式2的孔压,但模式1的负孔压要比模式2的大。
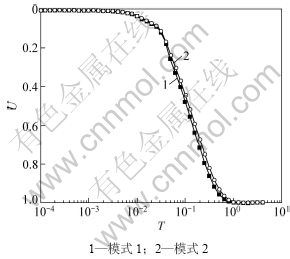
图9 荷载两级线性施加时地基的固结度曲线
Fig.9 Consolidation rate of sand drains foundation under double-ramp loading
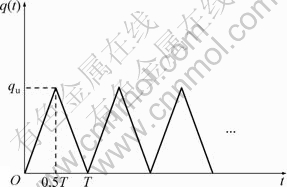
图10 三角形循环荷载
Fig.10 Triangular cyclic loading
图12所示为三角形循环荷载作用下地基有效应力曲线。从图12可以看出:有效应力呈震荡上升趋势,同样其震荡幅度不随时间减小,但其震荡中线逐渐趋于一定值。模式1的有效应力要比模式2的大。
5.3 梯形循环荷载
地基在如图13所示的梯形循环荷载作用下,T=180 d,t1=30 d,t2=90 d,t3=120 d,qu=50 kPa,地基超静孔压曲线和附加有效应力曲线如图14和图15所示,可以看出其与三角形循环荷载作用时有相似的规律。
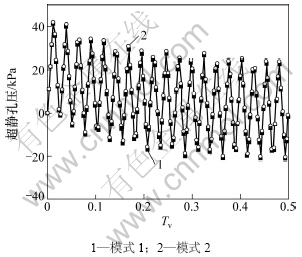
图11 三角形循环荷载作用下地基超静孔压曲线
Fig.11 Excess pore-water pressure of sand drains foundation under triangular cyclic loading
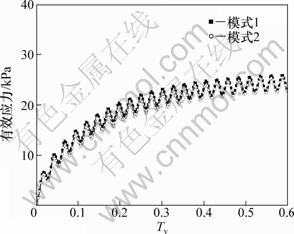
图12 三角形循环荷载作用下地基有效应力曲线
Fig.12 Effective stress of sand drains foundation under triangular cyclic loading
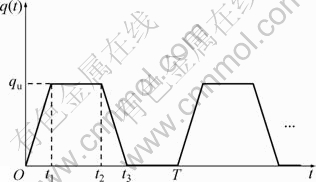
图13 梯形循环荷载
Fig.13 Trapezium cyclic loading
5.4 抛物线形循环荷载
如图16所示为二次抛物线形循环荷载,抛物线方程为:
![]() (54)
(54)
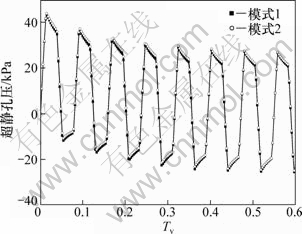
图14 梯形循环荷载下地基超静孔压曲线
Fig.14 Excess pore-water pressure of sand drains foundation under trapezium cyclic loading
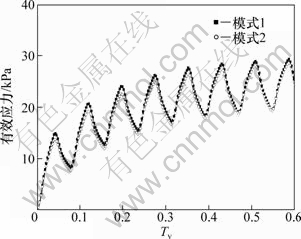
图15 梯形循环荷载下地基有效应力曲线
Fig.15 Effective stress of sand drains foundation under trapezium cyclic loading
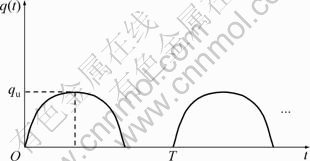
图16 抛物线形循环荷载
Fig.16 Parabolic cyclic loading
如t1=60 d,T=180 d,qu=50 kPa,在循环荷载作用下,考虑渗透系数呈线性变化。地基的超静孔压曲线和附加有效应力曲线如图17和图18所示。其中,X为逼近抛物线的直线段段数。
从图17和图18可以看出:它们均具有很好的收敛性,当X为2时4时有较大差别,X为4时与10时差别不大,而X为10时与为100时的孔压曲线和有效应力曲线基本上重合,这说明采用直线段模拟荷载随时间曲线变化是很有效的。
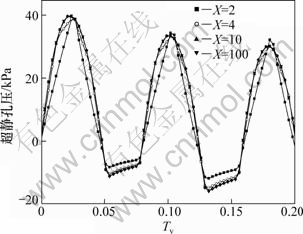
图17 抛物线形循环荷载下地基超静孔压曲线
Fig.17 Excess pore-water pressure of sand drains foundation under parabolic cyclic loading
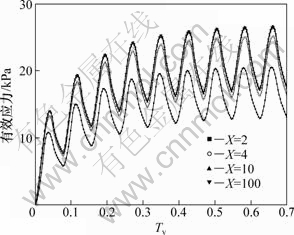
图18 抛物线形循环荷载下地基有效应力曲线
Fig.18 Effective stress of sand drains foundation under parabolic cyclic loading
6 结论
(1) 在荷载分级施加时,考虑涂抹区渗透系数线性变化时地基固结速度比假设其不变时的快。
(2) 在循环荷载作用下,砂井地基超静孔压呈震荡减小趋势,在卸荷时可能会产生负压,震荡幅度并不随时间减小,但其震荡中线逐渐趋于一定值;考虑涂抹区渗透系数线性变化时的正孔压比假设其不变时的小,而负超静孔压更大。
(3) 在循环荷载作用下,地基有效应力呈震荡上升趋势;同样,其震荡幅度不随时间减小,震荡中线逐渐趋于一定值。考虑渗透系数线性变化时有效应力比假设其不变时的大。
(4) 当荷载随时间曲线变化时,采用多段直线段逼近荷载曲线是求解此问题的有效方法。
参考文献:
[1] Barron R A. Consolidation of fine grained soil by drains wells[J]. Transactions of ASCE, 1948, 113: 718-742.
[2] Richart, Jr F E. A review of the theories for sand drains[J]. Proc ASCE, 1957, 83(S3): 1-38.
[3] Yoshikuni H, Nakanodo H. Consolidation of soils by vertical drain wells with finite permeability[J]. Soils and Foundations, 1974, 14(2): 35-46.
[4] Hansbo S, Jamiolkowski M, Kok L. Consolidation by vertical drains[J]. Geotechnique, 1981, 31(1): 45-46.
[5] 曾国熙,王铁儒,顾尧章. 砂井地基的若干问题[J]. 岩土工程学报,1981, 3(3): 74-81.
ZENG Guo-xi, WANG Tie-ru, GU Yao-zhang. Several problems of sand drains[J]. Chinese Journal of Geotechnical Engineering, 1981, 3(3): 74-81.
[6] Hart E G, Kindner R L, Boyer W C. Analysis for partially penetrating sand drains[J]. Journal of Soil Mechanics and Foundation Division, ASCE, 1958, 84(S4): 1-15.
[7] 陈根媛. 多层地基的一维固结计算方法与砂井地基计算的改进建议[J ]. 水利水运科学研究, 1984, 5(2) :18-29.
CHEN Gen-yuan. One-dimensional consolidation of layered systems and a suggestion for improving calculation of sand-drained subsoil[J]. Journal of Nanjing Hydraulic Research Institute, 1984, 5(2): 18-29.
[8] 谢康和. 砂井地基: 固结理论、数值分析与优化设计[D]. 杭州: 浙江大学建筑工程学院, 1987: 1-62.
XIE Kang-he. Sand drained ground: Analytical & numerical solutions of consolidation and optimal design[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 1987: 1-62.
[9] 谢康和, 周开茂. 未打穿竖向排水井地基固结理论[J]. 岩土工程学报, 2006, 28(6): 679-684.
XIE Kang-he, ZHOU Kai-mao. Consolidation theory for soft soil with partially penetrated vertical drains[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 679-684.
[10] 卢萌盟, 谢康和, 张玉国, 等. 考虑土体水平渗透系数变化的复合地基固结解[J]. 浙江大学学报: 工学版, 2008, 41(11): 1996-2001.
LU Meng-meng, XIE Kang-he, ZHANG Yu-guo, et al. Analytical solution for consolidation of composite foundation accounting for variation of soil horizontal permeability coefficient[J]. Journal of Zhejiang University: Engineering Science, 2008, 41(11): 1996-2001.
[11] Tang X W, Onitsuka K. Consolidation of double- layered ground with vertical drains[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25: 449-465.
[12] Bergado D T, Asakami H, Alfaro M C, et al. Smear effects of vertical drains on soft Bangkok clay[J]. Journal of Geotechnical Engineering, 1991, 117(10): 1509-1530.
[13] Indraratna B, Redana I W. Babaoratory determination of smear zone due to vertical drain installation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(2): 180-184.
[14] Sharma J S, Xiao D. Characterization of a smear zone around vertical drains by large-scale laboratory tests[J]. Canadian Geotechnical Journal, 2000, 37(6): 1265-1271.
[15] XIE Kang-he, LU Meng-meng, LIU Gan-bin. Equal strain consolidation for stone columns reinforced foundation[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2009, 33(15): 1721-1735.
[16] Olson R E. Consolidation under time dependent loading[J]. Journal of the Geotechnical Engineering Division, 1977, 103(GT1): 55-60.
[17] Tang X W, Onitsuka K. Consolidation by vertical drains under time-dependent loading. International[J]. Journal for Numerical and Analytical Methods in Geomechanics, 2000, 24(9): 739-751.
[18] Leo C J. Equal strain consolidation by vertical drains[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(3): 316-327.
[19] Zhu G F, Yin J H. Finite element analysis of consolidation of soils with vertical drain[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2000, 24(4): 337-366.
[20] 耿雪玉, 蔡袁强, 徐长节. 复杂荷载作用下考虑下卧层三维渗流的未打穿竖井地基固结分析[J]. 岩土力学, 2008, 29(6): 1521-1529.
GENG Xue-yu, CAI Yuan-qiang, XU Chang-jie. Soil of consolidation with partially penetrated vertical drains under complicated loadings considering three-dimensional seepage in soil beneath vertical drain[J]. Rock and Soil Mechanics, 2008, 29(6): 1521-1529.
[21] Conte E, Troncone A. Radial consolidation with vertical drains and general time-dependent loading[J]. Canadian Geotechnical Journal, 2009, 46(1): 25-36.
(编辑 陈灿华)
收稿日期:2011-06-26;修回日期:2011-09-10
基金项目:国家自然科学基金资助项目(51009135)
通信作者:郭彪(1982-),男,四川安岳人,博士,从事地基处理研究;电话:13883968109;E-mail:gb25891775@163.com
摘要:对随时间任意变化的荷载作用下砂井地基固结问题进行研究。首先推导考虑涂抹效应、井阻作用、土体内径竖向组合渗流、变荷载以及涂抹区水平渗透系数线性连续变化等因素的解析解;然后,将上部荷载进行傅里叶变换转化为三角级数的形式,即将复杂荷载分解为很多简单的正余弦函数之和,通过简单荷载作用下响应的叠加得到原复杂荷载作用下的响应,由此得到一种便于工程应用的简单方法;编制计算程序,与传统解析解进行对比;最后,分析几种荷载模式下砂井地基的固结性状,包括多级线性加载、三角形循环荷载、矩形循环荷载等一般模式,并通过用多段直线段逼近曲线的方法,分析抛物线形循环荷载作用下地基的固结特性。研究结果表明:本文方法合理,具有广泛的适用性。


