J. Cent. South Univ. (2016) 23: 2616-2629
DOI: 10.1007/s11771-016-3323-6
Proportional integral derivative controller design using Legendre orthogonal functions
Reza Moradi, Mohammad Tabatabaei
Department of Electrical Engineering, Khomeinishahr Branch, Islamic Azad University, Isfahan, Iran
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract:
The Legendre orthogonal functions are employed to design the family of PID controllers for a variety of plants. In the proposed method, the PID controller and the plant model are represented with their corresponding Legendre series. Matching the first three terms of the Legendre series of the loop gain with the desired one gives the PID controller parameters. The closed loop system stability conditions in terms of the Legendre basis function pole (λ) for a wide range of systems including the first order, second order, double integrator, first order plus dead time, and first order unstable plants are obtained. For first order and double integrator plants, the closed loop system stability is preserved for all values of λ and for the other plants, an appropriate range in terms of λ is obtained. The optimum value of λ to attain a minimum integral square error performance index in the presence of the control signal constraints is achieved. The numerical simulations demonstrate the benefits of the Legendre based PID controller.
Key words:
1 Introduction
Employing orthogonal functions like Legendre orthonormal functions in system identification, model reduction and controller design have been increased nowadays. Shifted Legendre polynomials have been utilized to identify time varying plants [1]. Legendre operational matrix of integration has been utilized for the identification of linear systems [2]. Legendre orthogonal functions have been employed to approximate analytic functions, too [3]. The orthogonal functions such as classical Laguerre and Legendre functions have been employed in control applications. In Ref. [4], a robust adaptive controller based on Legendre orthogonal functions has been proposed. Legendre orthogonal functions have been employed to design optimal controllers, too [5-7].
On the other hand, the family of proportional- integral-derivative (PID) controllers (including PI, PD and PID controllers) are still widely used to control the real plants [8]. The main benefits of these controllers such as design simplicity and disturbance rejection capability have increased new analytical methods to tune them [9-10]. The well-known Ziegler and Nichols design tables have been known the first attempts to design PID controllers [11]. Optimization based methods have been employed to design PID controllers. [12-13]. These methods could not give explicit relations for PID controller parameters. PID controller based on phase margin and crossover frequency specifications has been proposed, too [14]. Internal model control (IMC) approach has been employed for PID controller design in the literature. IMC-PID controllers for first order plus dead time (FOPDT) and second order plus dead time (SOPDT) plants have been presented [15-16]. The IMC based PID controllers could only be employed to control some special plants.
The moment matching based PID controller design methods have been considered. In Ref. [17], a moment matching based PID controller has been proposed. The plant moments are calculated based on the impulse response data. The main disadvantage of this method is that the resultant PID controller could not guarantee the closed loop system stability. Taylor series expansion has been utilized to design a proportional differential (PD) controller for FOPDT plants, too [18]. The PD controller parameters are obtained by matching the corresponding terms of the Taylor series coefficients of the closed loop system with the desired closed loop transfer function. The application of the proposed method is confined to only FOPDT plants.
PID controller design based on orthogonal functions has been considered in the literature. An orthogonal function based digital PID controller has been designed to meet some time domain specifications [19]. PID controller for multi input multi output (MIMO) systems based on shifted Legendre polynomials has been designed, too [20]. In this work, the state space equations have been converted to a set of algebraic equations by expanding the system input and output variables into their orthogonal functions. In Ref. [21], a PID controller design approach for integer and fractional order plants based on orthogonal Block pulse, Walsh and Haar Wavelets functions have been proposed.
In this work, Legendre orthogonal functions are employed to design family of PID controllers for a variety of plant models. Matching the first two Legendre series expansion terms of the loop gain with the desired one gives the PI and PD controller parameters. For the PID controller case, the first three terms are matched. The proposed method could be utilized to control stable, unstable, non-minimum phase and integrating plants. The pole of the Legendre basis function could be appropriately selected to attain the closed loop system stability. The optimum value of this parameter is computed to have a minimum deviation from the desired closed loop step response according to the integral square error performance index. The practical limitations such as control signal constraints are also considered in the design procedure. The explicit relations for the PID controller parameters makes the proposed method distinguished from other PID controller design methods. The method could be employed to control a variety of plants such as first and second order, double integrator, unstable and FOPDT plants. The simulation results on several plant models demonstrate the advantages of this Legendre based PID controller.
2 Review on Legendre orthogonal functions
The inner product of two functions pi(t) and pj(t) is defined as
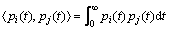 (1)
(1)
The 2-norm of function pi(t) could be calculated in accordance with relation (1) as
 (2)
(2)
Two functions pi(t) and pj(t) with normal length and zero inner product are called orthonormal, or:
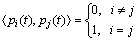 (3)
(3)
The L2 norm space consists of finite norm functions. Any function 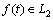 could be described in terms of orthonormal functions pk(t) as
could be described in terms of orthonormal functions pk(t) as
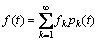 (4)
(4)
Taking the Laplace transform from both sides of Eq. (4) yields
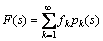 (5)
(5)
where series coefficients (fk) are given by
 (6)
(6)
According to the residue theorem, the series coefficients are calculated as
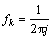
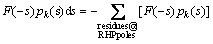 (7)
(7)
The Legendre orthonormal basis functions are defined as [22]
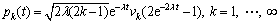 (8)
(8)
where vk(t) is defined as
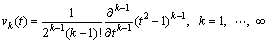 (9)
(9)
The Legendre orthonormal functions in Eq. (8) could be represented in the s-domain as
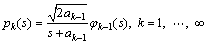 (10)
(10)
where

i=0, 1, …, ∞, k=1, …, ∞ (11)
The first three Legendre basis functions obtained from Eqs. (10) and (11) are

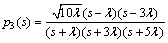 (12)
(12)
The product of each pair Legendre basis functions could be represented as the following Legendre series:
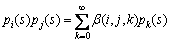 (13)
(13)
where some values of β(i, j, k) calculated are given by

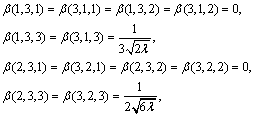
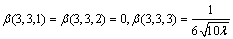 (14)
(14)
3 Using legendre functions to design PID controllers
In this section, a Legendre based PID controller is proposed. The design approach is based on approximating a strictly proper stable transfer function F(s) with the first three terms in its Legendre series expansion, or:
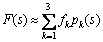 (15)
(15)
The controller design procedure is based on matching the product of the controller C(s) and the plant model G(s) with a desired loop gain transfer function L(s)
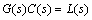 (16)
(16)
Consider a plant with the following transfer function:
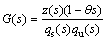 (17)
(17)
where z(s) and qs(s) are Hurwitz polynomials and qu(s) is the unstable part of the denominator of G(s) (including unstable poles of the plant). The degree of z(s), qu(s) and qs(s) are considered m, r and n, respectively. The nonnegative parameter θ determines the unstable zero of the plant. System (17) is a strictly proper transfer function, if the following relation is fulfilled:
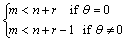 (18)
(18)
It means that the considered plant model includes a variety of strictly proper transfer function. It could be stable or unstable, minimum phase or non-minimum phase with utmost one unstable zero.
Based on dominant poles concept, the standard second-order transfer function is considered as the desired closed loop transfer function in many controller design methods. Moreover, the unstable zero in Eq. (17) could not be canceled through controller poles. Thus, it will be appeared in the closed loop transfer function. Therefore, the desired closed loop transfer function is considered as follows.
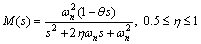 (19)
(19)
where η and ωn are the damping ratio and un-damped oscillations frequency, respectively. The parameter η is considered smaller than 1 and greater than 0.5 to have a fast response with minimum overshoot. The closed loop system transient response speed depends on the parameter ωn. The desired loop gain transfer function corresponding with the desired closed loop transfer function in Eq. (19) is calculated as
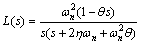 (20)
(20)
The transfer function in Eq. (20) has an unstable pole in s=0. Therefore, it could not be directly expanded in terms of the Legendre basis functions. Therefore, the transfer function in Eq. (20) should be rewritten in the following form
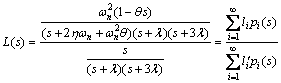 (21)
(21)
The first three Legendre series coefficients in Eq. (21) are calculated according to Eq. (7) as
 (22)
(22)
Stable plants in Eq. (17) (qu(s)=1), could be represented directly in the following Legendre series expansion form:
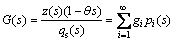 (23)
(23)
But, unstable plants could not directly be described in terms of their Legendre series. In this case, the transfer function in Eq. (17) should be rewritten as

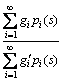 (24)
(24)
The transfer function of the PID controller is considered as
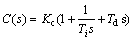 (25)
(25)
Considering (Td=0) or (Ti=∞) leads to PI and PD controllers, respectively. In the remainder of this section, the Legendre based design method for family of PID controllers are presented.
3.1 PI Controller design
Considering Td=0 in Eq. (25) yields the PI controller with the following transfer function
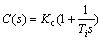 (26)
(26)
The PI controller in Eq. (26) could be represented with the following Legendre series expansion form:
 (27)
(27)
The first two Legendre series coefficients in Eq. (27) are obtained as
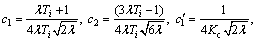
 (28)
(28)
Consider that the plant model is a stable transfer function described with its Legendre series expansion in Eq. (23). Now, substituting relations (21), (23) and (27) in Eq. (16) gives:
 (29)
(29)
Both sides of Eq. (29) could be converted into two Legendre series by employing the multiplication property of the Legendre functions in Eqs. (13) and (14). Matching the first two coefficients of these Legendre series yields the following equations:
 (30)
(30)
Substituting relations (28) in (30) yields the following PI controller parameters:
 (31)
(31)
For unstable plants, Eq. (24) should be utilized. Therefore, Eq. (29) should be replaced with the following expression:
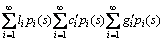 (32)
(32)
Simplifying Eq. (32) according to Eqs. (13) and (14) and matching the first two corresponding terms, gives:

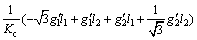 (33)
(33)
Solving Eq. (33) results in the following PI controller parameters
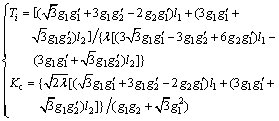 (34)
(34)
3.2 PD controller design
Substituting Ti=∞ in Eq. (25) yields the PD controller with the following transfer function:
 (35)
(35)
Unlike the PI or PID controller, PD controller does not have an integrator which is necessary for tracking constant signals. Therefore, this type of controller could be employed to control plants including at least one integrator in their transfer function. Thus, the plant model should be at least a type 1 transfer function which is compatible with the Legendre series expansion in Eq. (24). This means that Eq. (32) should be utilized to design Legendre based PD controllers.
The PD controller in Eq. (35) should be converted to the following Legendre series description:
 (36)
(36)
where the Legendre series coefficients in Eq. (36) are
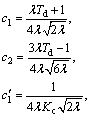
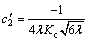 (37)
(37)
Considering Eqs. (13), (14) and (37) and matching the first two Legendre series coefficients in Eq. (32) gives the following expression:
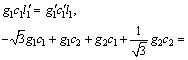
 (38)
(38)
According to Eqs. (37) and (38), the PD controller parameters could be obtained as
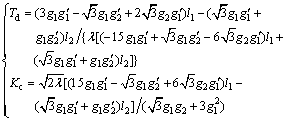 (39)
(39)
3.3 PID controller design
To design a Legendre based PID controller, its transfer function in Eq. (25) should be rewritten as
 (40)
(40)
where the Legendre series coefficients in Eq. (40) are obtained as
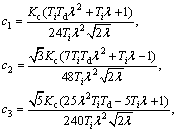
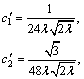
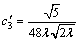 (41)
(41)
Similar to the PI controller design procedure, designing a PID controller for strictly proper stable plants represented by transfer function (23), requires Eq. (29). Simplifying Eq. (29) according to relations (41), (13) and (14) and matching the first three corresponding terms in the Legendre series yields the following three relations:
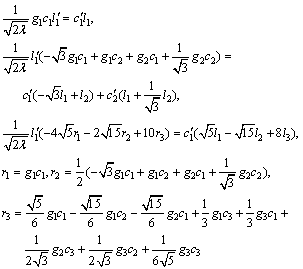 (42)
(42)
According to Eqs. (41) and (42), the PID controller parameters are calculated as
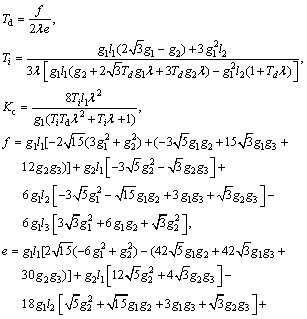
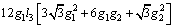 (43)
(43)
To design Legendre based PID controller for unstable plants, the following relations should be satisfied according to Eq. (32)
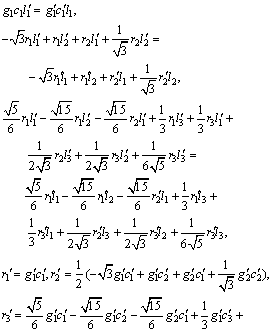
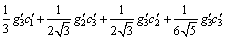 (44)
(44)
The PID controller parameters determined from Eqs. (41) and (44) are
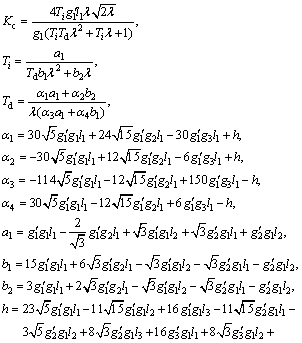
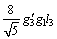 (45)
(45)
4 Selection of Legendre function pole location
The proposed method is based on approximating the loop gain Legendre series expansion with its first three terms. Therefore, the effect of the neglected terms in the Legendre series expansion on the closed loop system stability should be verified. The closed loop system is stable if all the roots of the closed loop characteristic equation lie in the open left-half plane (LHP).
For the PI controller case, the closed loop characteristic equation becomes
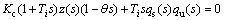 (46)
(46)
The closed loop system characteristic equation for the PD controller is
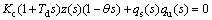 (47)
(47)
And for the PID controller, we have the following closed loop characteristic equation:
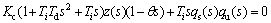 (48)
(48)
The Legendre pole location parameter (λ) should be appropriately selected such that the polynomials (46), (47) and (48) are the Hurwitz polynomials. This results in some conditions in terms of the Legendre basis function pole to assure the stability requirements. In the obtained stability region for λ, the optimum value of this parameter to minimize a performance index should be found. The Legendre basis function pole location should be determined so that the difference between the desired closed loop unit step response (yd(t)) and the closed loop unit step response (y(t)) is minimized. This means that the following integral square error performance index should be minimized:
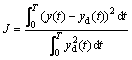 (49)
(49)
where T could be considered the settling time of the closed loop system step response. Optimizing the cost function (49) improves the closed loop system performance but could increase the control signal (u(t)). The control signal must have admissible values considering practical limitations such as actuator saturation and so on. This means that the controller parameters (λ, ωn, η) should be obtained by solving the following constrained optimization problem
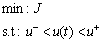 (50)
(50)
where u+ and u- are the upper and lower control signal bounds which should be selected according to the practical limitations. In conclusion, we can say that the controller parameters η, ωn and λ should be adjusted to attain the best closed loop system step response in the presence of the control signal constraints.
5 Applying proposed controller on a lot of plant models
In this section, the performance of the proposed Legendre based PI, PD and PID controllers to control a variety of plants is studied. For each plant model, the stability conditions in terms of the design parameters are extracted.
5.1 Legendre based PI and PID controller design for first-order plants
Consider the following first-order plant
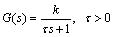 (51)
(51)
where k and τ are the steady state gain and the time constant of the plant, respectively.
The first three Legendre series coefficients of system (51) are computed as
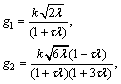
 (52)
(52)
Substituting expressions in Eq. (52) in Eq. (31) leads to the following PI controller parameters:
 (53)
(53)
The closed loop characteristic equation according to relations (46) and (51) is obtained as
 (54)
(54)
According to Eq. (54), the closed loop system is stable if and only if the following conditions are fulfilled
 (55)
(55)
According to Eq. (53), we have
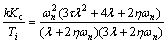 (56)
(56)
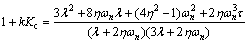 (57)
(57)
Both Eqs. (56) and (57) are positive, considering 0.5≤η≤1 according to Eq. (19). Therefore, the proposed Legendre based PI controller for first-order plants yields to a stable closed loop system for all values of parameter λ.
The PID controller parameters calculated in accordance with Eq. (43) are
 (58)
(58)
The closed loop characteristic equation according to relations (48) and (51) becomes
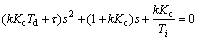 (59)
(59)
According to Eq. (59), the closed loop system stability depends on satisfaction of the following inequalities:
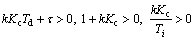 (60)
(60)
Relation (58) gives
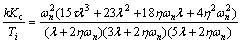 (61)
(61)

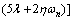 (62)
(62)

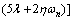 (63)
(63)
According to Eq. (19), it is obvious that the right-hand sides of Eqs. (61), (62) and (63) are always positive. Therefore, the closed loop system obtained from the Legendre based PID controller for the first-order plants is always stable (independent of the value of the parameter λ). The following example illustrates the effectiveness of the proposed Legendre based PI and PID controllers to control the first order plants.
Example 1: Consider system (51) with k=2, τ=0.5. To have a well damped transient response four times faster than the plant step response, the following design parameters are considered:
 (64)
(64)
The upper and lower control signal bounds are considered as -5 and 5, respectively. The MATLAB FMINCON function is employed to solve the optimization problem in Eq. (50). The optimal value of λ and the transfer functions of the resultant PI and PID controllers with their corresponding performance indexes are given in Table 1. Figure 1 shows good matching between the closed loop unit step response and the desired one. Moreover, the control signal requirements are fulfilled.
Table 1 Controller properties corresponding to Examples 1-6


Fig. 1 Closed loop unit step responses (a) and control signal (b) in Example 1
5.2 Legendre based PD controller design for integrating second-order plants
An integrating second-order plant with the following transfer function is considered:
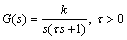 (65)
(65)
The transfer function (65) should be rewritten in the following Legendre series expansion form:
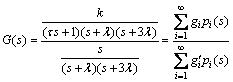 (66)
(66)
The first two Legendre series coefficients in Eq. (66) are determined as

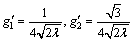 (67)
(67)
The PD controller parameters are obtained according to Eq. (39) as follows:
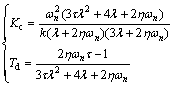 (68)
(68)
The closed loop characteristic equation for the PD controller is calculated as
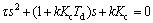 (69)
(69)
The closed loop system stability conditions are
 (70)
(70)
Substituting relation (68) in the left-hand side of inequalities in Eq. (70) gives
 (71)
(71)
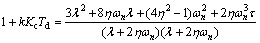 (72)
(72)
The right-hand sides of Eqs. (71) and (72) are positive for all values of λ. This ensures the closed loop system stability for integrating second-order plants controlled by the Legendre based PD controller. The next example is given to show the usefulness of the Legendre based PD controller.
Example 2: The plant parameters in Eq. (65) are considered k=2, τ=10. The design parameters are selected as
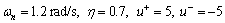 (73)
(73)
The PD controller parameters and the optimal value of λ are shown in Table 1. Figure 2 gives a comparison between the closed loop system step response and the desired one. This comparison proves the performance of the Legendre based PD controller as well. Moreover, the control signal shown in Fig. 2 is in the admissible range.

Fig. 2 Closed loop unit step responses (a) and control signal (b) in Example 2
5.3 Legendre based PD controller design for double- integrator plants
A double-integrator plant could describe with the following transfer function:
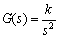 (74)
(74)
The double integrator plant is an unstable system. Thus, its transfer function should be rewritten as
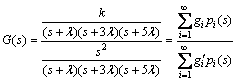 (75)
(75)
The following are the first two Legendre series coefficients in Eq. (75):

 (76)
(76)
The PD controller parameters determined from Eq. (39) are
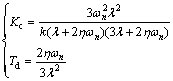 (77)
(77)
The closed loop characteristic equation is given by
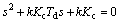 (78)
(78)
To attain the closed loop system stability, the following conditions should be satisfied
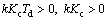 (79)
(79)
According to relation (77), the PD controller parameters are positive. It means that inequalities in relation (79) are fulfilled. This results in a stable closed loop system for a double-integrator plant controlled by a Legendre based PD controller (for all values of parameter λ).
Example 3: Consider the plant (74) with k=0.75. The following design parameters are considered:
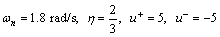 (80)
(80)
Table 1 shows the optimal value of the parameter λ and the PD controller parameters. Figure 3 shows that the closed loop system unit step response is similar to the corresponding desired one. Moreover, Fig. 3 demonstrates that the control signal is in the permissible range.
5.4 Legendre based PI controller design for second- order plants
Consider a second-order plant with two real poles as follows
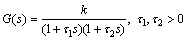 (81)
(81)
The first two Legendre series coefficients in Eq. (81) are calculated as

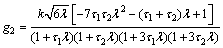 (82)
(82)

Fig. 3 Closed loop unit step responses (a) and control signal (b) in Example 3
Equation (31) gives the following PI controller parameters:
 (83)
(83)
The closed loop system poles are the roots of the following third-order polynomial
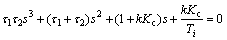 (84)
(84)
According to the Routh-Hurwitz stability criterion, the necessary and sufficient conditions for the closed loop system stability are given by
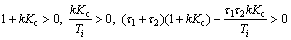 (85)
(85)
Placing PI controller parameters in Eq. (83) in the left sides of inequalities in (85) gives:
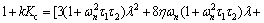
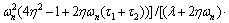
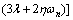 (86)
(86)
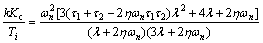 (87)
(87)
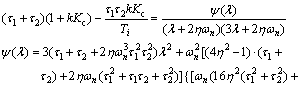
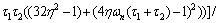
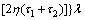 (88)
(88)
It is obvious that the right sides of Eqs. (86) and (88) are always positive. Thus, the closed loop system stability depends on positivity of the right side of Eq. (87). This yields to the following stability conditions:
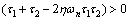 or
or
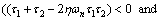
 (89)
(89)
The performance of the Legendre based PI controller for a second-order plant is verified in the next example.
Example 4:Consider plant (81) with k=2, τ1=0.8, and τ2=0.5, the design parameters are chosen as
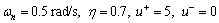 (90)
(90)
The optimum value of the Legendre basis function and the PI controller parameters are given in Table 1. The comparison between the closed loop system unit step response and the desired one in Fig. 4, demonstrates the benefits of the proposed Legendre based PI controller. Moreover, as could be seen from Fig. 4, the control signal constraints are fulfilled.
5.5 Legendre based PID controller design for an unstable first-order plant
In this section, the Legendre base PID controller is employed to control an unstable first-order plant. Consider an unstable first-order plant with the following transfer function
 (91)
(91)
The transfer function (91) should be modified as
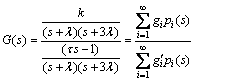 (92)
(92)
The first three Legendre series coefficients in Eq. (92) are determined as
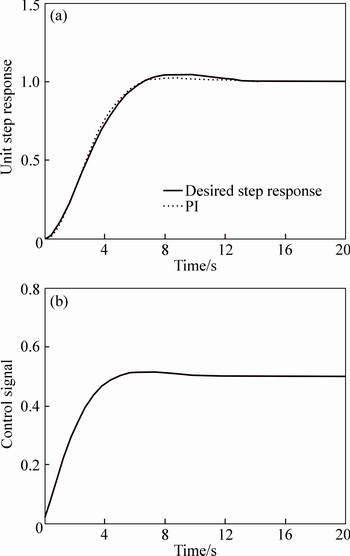
Fig. 4 Closed loop unit step responses (a) and control signal (b) in Example 4
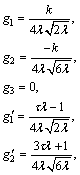
 (93)
(93)
Based on relations (45) and (93), the following PID controller parameters are obtained:
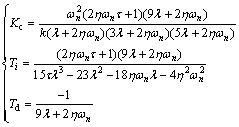 (94)
(94)
The closed loop system characteristic equation is given by
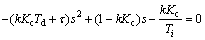 (95)
(95)
The following conditions should be met to attain the closed loop system stability
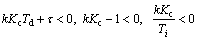 (96)
(96)
The left sides of inequalities (96) are calculated in accordance with Eq. (94) as

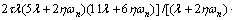
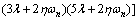 (97)
(97)
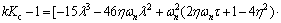
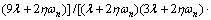
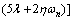 (98)
(98)
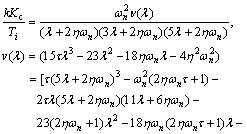
 (99)
(99)
According to relations (96), (97), (98) and (99), the sufficient conditions for the closed loop system stability are

 (100)
(100)
The next example investigates the effectiveness of the Legendre based PID controller to control unstable first-order plants.
Example 5: Consider the unstable plant in Eq. (91) with k=1 and τ=0.02. The design parameters are considered as
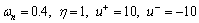 (101)
(101)
The optimal value of λ and PID controller parameters are given in Table 1. The desired step response, the closed loop system step response and the control signal shown in Fig. 5, demonstrate the performance of the proposed PID controller in the presence of the control signal constraints.
5.6 Legendre based PI controller design for FOPDT plants
In this section, the benefit of the Legendre based PI controller to control a FOPDT plant is investigated. An FOPDT plant with the following transfer function is
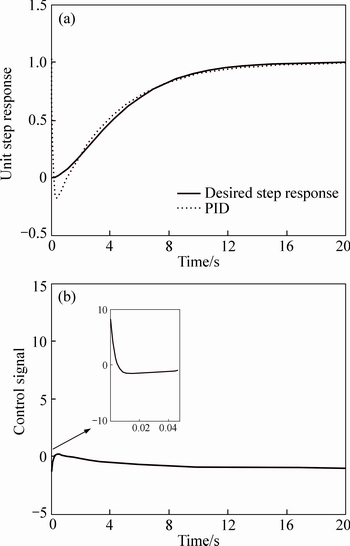
Fig. 5 Closed loop unit step responses (a) and control signal (b) in Example 5
considered:
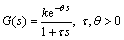 (102)
(102)
The proposed method could be used only for rational transfer functions. Thus, the delay term in Eq. (102) should be approximated based on Taylor expansion as
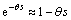 (103)
(103)
Substituting relationship Eq. (103) in (102) gives the following approximated plant model:
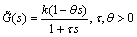 (104)
(104)
The transfer function in Eq. (104) is not a strictly proper transfer function and should be modified to the following Legendre series expansion form:
 (105)
(105)
where
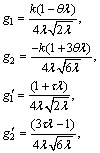
 (106)
(106)
The Legendre based PI controller parameters for FOPDT plant are calculated as
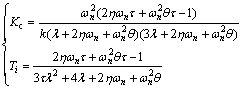 (107)
(107)
The closed loop system characteristic equation (including the approximated model) is
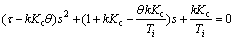 (108)
(108)
The closed loop system is stable if the following inequalities are satisfied
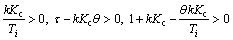 (109)
(109)
The obtained expressions for PI controller parameters in Eq. (107) give:
 (110)
(110)
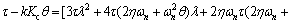
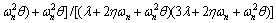 (111)
(111)
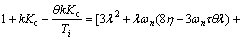
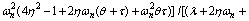
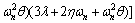 (112)
(112)
It is obvious that relations (110) and (111) are always positive. Thus, the positivity of relation (112) leads to the closed loop system stability. According to relation (112), the following sufficient condition for the closed loop system is derived:
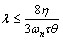 (113)
(113)
The next example is given to illustrate the usefulness of the Legendre based PI controller for FOPDT plants.
Example 6:Consider the FOPDT plant Eq. (102) with k=2, τ=0.5 and θ=0.1. The design parameters are selected as
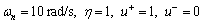 (114)
(114)
Table 1 shows the optimum value of λ and the transfer function of PI controller. The PI controller is designed based on the approximated model (104) but is applied to plant (102). The performance of the Legendre based PI controller is compared with the Cohen-Coon PI already proposed [23]. In this method, the PI controller parameters are calculated according to the following relations:
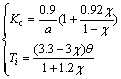 (115)
(115)
where
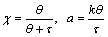 (116)
(116)
The Cohen-Coon PI controller parameters are calculated as
 (117)
(117)
In Fig. 6, the performance of the Legendre based PI and the Cohen-Coon PI are compared. Figure 6 demonstrates the benefits of the Legendre based PI controller comparing with the Cohen-Coon PI in terms of the transient response specifications and control signal limitations.
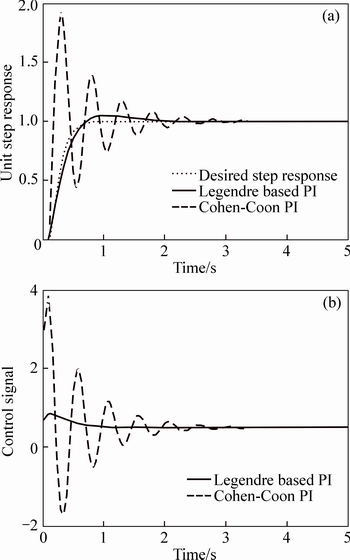
Fig. 6 Closed loop unit step responses (a) and control signal (b) in Example 6
6 Conclusions
1) The proposed Legendre series based approach could be utilized as an efficient analytical tool to design the family of PID controllers (including PI, PD and PID controllers) as well. The explicit relations obtained for the PID controller parameters make the proposed design method distinguished from other usual PID design methods.
2) The performance of the proposed method is studied for a variety of plants with different transfer functions. The proposed method could be utilized to control stable, unstable, integrating and non-minimum phase plants.
3) The pole of the Legendre basis function could be appropriately adjusted to attain the closed loop system stability. It is proved that Legendre based PI and PID controller could stabilize first order plants for all values of λ. The same result is obtained when a double- integrator plant is controlled by a Legendre based PD controller.
4) The optimal value of λ for minimizing an integral square error performance index (considering control signal limitations) is calculated.
References
[1] HWANG C, GUO T Y. Parameter identification of a class of time-varying systems via orthogonal shifted Legendre polynomials [J]. Journal of the Franklin Institute, 1984, 318(1): 56-69.
[2] PARASKEVOPOULOS P N. Legendre series approach to identification and analysis of linear systems [J]. IEEE Transactions on Automatic Control, 1985, 30(6): 585-589.
[3] JUNG S M. Approximation of analytic functions by Legendre functions [J]. Nonlinear Analysis: Theory, Methods & Applications, 2009, 71(12): e103-e108.
[4] WANG H, YU S. Tracking control of robot manipulators based on orthogonal neural network [J]. International Journal of Modelling, Identification and Control, 2010, 11(1/2): 130-135.
[5] MOHAN B M, KAR S K. Optimal control of singular systems via orthogonal functions [J]. International Journal of Control, Automation and Systems, 2011, 9(1): 145-150.
[6] MARZBAN H R, RAZZAGHI M. Optimal control of linear delay systems via hybrid of block-pulse and Legendre polynomials [J]. Journal of the Franklin Institute, 2004, 341(3): 279-293.
[7] RAZZAGHI M, YOUSEFI S. Legendre Wavelet method for constrained optimal control problems [J]. Mathematical Methods in the Applied Sciences, 2002, 25(7): 529-539.
[8] BENNETT S. The past of PID controllers [J]. Annual Reviews in Control, 2001, 25: 43-53.
[9]  T. PID Controllers: Theory, design and Tuning [M]. USA: Instrumentation Society of America, 1995: 120-273.
T. PID Controllers: Theory, design and Tuning [M]. USA: Instrumentation Society of America, 1995: 120-273.
[10] DATTA A, HO M T, BHATTACHARYYA S P. Structure and synthesis of PID controllers [M]. London, UK: Springer-Verlag, 2000: 15-235.
[11] ZIEGLER J G, NICHOLS N B. Optimum settings for automatic controller [J]. Journal of Dynamic Systems, Measurement, and Control, 1993, 115(2B): 220-222.
[12] WANG J S. Optimal design of PI/PD controllers for non-minimum phase system [J]. Transactions of the Institute of Measurement and Control, 2006, 28(1): 27-35.
[13] HERREROS A, BAEYENS E, PERAN J R. Design of PID-type controllers using multiobjective genetic algorithms [J]. ISA Transactions, 2002, 41(4): 457-472.
[14] MIKHALEVICH S S, BAYDALI S A, MANENTI F. Development of a tunable method for PID controllers to achieve the desired phase margin [J]. Journal of Process Control, 2015, 25: 28-34.
[15] VILANOVA R. IMC based robust PID design: Tuning guidelines and automatic tuning [J]. Journal of Process Control, 2008, 18(1): 61-70.
[16] PANDA R C, YU C C, HUANG H P. PID tuning rules for SOPDT systems: review and some new results [J]. ISA Transactions, 2004, 43(2): 283-295.
[17] RAMASAMY M, SUNDARAMOORTHY S. PID controller tuning for desired closed loop responses for SISO systems using impulse response [J]. Computers & Chemical Engineering, 2008, 32(8): 1773-1788.
[18] XU L. A proportional differential control method for a time-delay system using the Taylor expansion approximation [J]. Applied Mathematics and Computation, 2014, 236(1): 391-399.
[19] HORNG I R, CHOU J H. Digital PID controller design via general discrete orthogonal polynomials [J]. International Journal of Control, 1988, 47(1): 188-192.
[20] AYADI B, BRAIEK N B. MIMO PID controllers synthesis using orthogonal functions [C]// Proceedings of the 16th IFAC World Congress. Prague, Czech Republic: IFAC, 2005: 508-513.
[21] BOUAFOURA M K, BRAIEK N B. PIλDμ controller design for integer and fractional plants using piecewise orthogonal functions [J]. Communications in Nonlinear Science and Numerical Simulation, 2010, 15(5): 1267-1278.
[22] HEUBERGER P S C, van den HOF P M J, WAHLBERG B. Modelling and identification with rational orthogonal basis functions [M]. London, UK: Springer-Verlag, 2005: 41-59.
[23] COHEN G H, COON G A. Theoretical consideration of retarded control [J]. Transactions of American Society of Mechanical Engineers, ASME, 1953, 75(1): 827-834.
(Edited by FANG Jing-hua)
Received date: 2015-08-06; Accepted date: 2015-12-10
Corresponding author: Mohammad Tabatabaei PhD, Assistant Professor; Tel: +98-31-33660011; Fax: +98-31-33660088; E-mail: tabatabaei@iaukhsh.ac.ir
Abstract: The Legendre orthogonal functions are employed to design the family of PID controllers for a variety of plants. In the proposed method, the PID controller and the plant model are represented with their corresponding Legendre series. Matching the first three terms of the Legendre series of the loop gain with the desired one gives the PID controller parameters. The closed loop system stability conditions in terms of the Legendre basis function pole (λ) for a wide range of systems including the first order, second order, double integrator, first order plus dead time, and first order unstable plants are obtained. For first order and double integrator plants, the closed loop system stability is preserved for all values of λ and for the other plants, an appropriate range in terms of λ is obtained. The optimum value of λ to attain a minimum integral square error performance index in the presence of the control signal constraints is achieved. The numerical simulations demonstrate the benefits of the Legendre based PID controller.


