Trans. Nonferrous Met. Soc. China 22(2012) s198-s206
Random dynamic response of crack in functionally graded materials layer for plane problem
ZHANG Hui-zhan1, 2, ZHAO Xiao-hua3, ZHANG Jia-zhen1, ZHOU Zhen-gong2
1. Beijing Aeronautical Science and Technology Research Institute of COMAC, Beijing 102211, China;
2. Center for Composite Materials, Harbin Institute of Technology, Harbin 150001, China;
3. Department of Civil Engineering, Shantou University, Shantou 515063, China
Received 9 July 2012; accepted 10 September 2012
Abstract:
In order to dynamically analyze a crack in a functionally graded materials layer for plane problem under dynamic loadings, a stochastic model is established for plane problem in which the material properties of the functionally graded materials layer vary randomly in the thickness direction, and the crack is parallel to the materials faces. A pair of dynamic loadings applied on the crack faces are treated as stationary stochastic processes of time. By dividing the functionally graded materials layer into several sub-layers, this problem is reduced to the analysis of laminated composites containing a crack, the material properties of each layer being random variables. A fundamental problem is constructed for the solution. Based on the use of Laplace and Fourier transforms, the boundary conditions are reduced to a set of singular integral equations, which can be solved by the Chebyshev polynomial expansions. The stress intensity factor history with its statistics is analytically derived. Numerical calculations are provided to show the effects of the related parameters. The results show that the increase of crack length, random field parameter β and crack location ratio h2/h leads to the increase of the mathematical expectation and standard deviation of normalized stress intensity factor history.
Key words:
functionally graded materials; crack; dynamic response; stochastic; stress intensity factor;
1 Introduction
Cracks may be induced in functionally graded materials (FGM) during manufacturing process, as well as in-service loading conditions. Crack failure is one of the most dominant failure mechanisms in the materials. MA et al [1] analyzed the dynamic behavior of two collinear cracks in an FGM layer bonded to dissimilar half planes under anti-plane shear waves. YUE et al [2] presented the analysis for an elliptical crack that is perpendicular to a functionally graded interfacial zone between two fully-bonded solids. MA et al [3] studied the time-harmonic response of two parallel cracks in FGMs. LI and GUO [4] analyzed the transient response of a crack lying at the interface between an FGM strip and an elastic substrate of finite width under antiplane shear impact loads. CHEN and CHUE [5] dealt with the anti-plane problem of two bonded functionally graded finite strips. TORSHIZIAN and KARGARMOVIN [6] studied an internal crack located within an FGM strip bonded between two dissimilar half-planes and anti-plane loading was considered. Both the conventional finite element method and the boundary element method are also widely used in the analysis of dynamic fracture of FGMs, such as TAN and MEGUID [7], 
et al [8]. HE et al [9] studied the effect of fiber characteristics on fracture behavior of Cf/SiC composites. LOU et al [10] analyzed the fracture behavior of B2-ordered iron aluminide with Mn addition. KOSTREVA et al [11] considered the modeling of fatigue fracture under stationary stochastic loading conditions. LI et al [12] presented high cycle fatigue and fracture behavior of 2124-T851 aluminum alloy. GAIDAI et al [13] discussed the effect of fatigue- induced crack propagation on the stochastic dynamics of a nonlinear structure. GAO et al [14] dealt with the fracture behavior of high strength Mg-Gd-Y-Zr magnesium alloy.
In those studies, material properties, loadings and crack geometry were always assumed to be deterministic. Thus, a deterministic approach might be applied for the analysis. Nevertheless, because of the difficulty in manufacturing process, material properties of FGMs may not be tailored exactly as the same as they are expected. In fact, their magnitudes can only be guaranteed within a reasonable range. For most cases, material properties of FGMs change randomly with field position and should be described as random fields. Actual loadings, such as wind and seismic loading, usually vary randomly with time. It is no longer reasonable to describe loadings in a deterministic way, and a stochastic description of loading process is required. All of these show the random nature of material damage processes, which suggests a probabilistic rather than a deterministic approach to solve the problem associated with dynamic fracture of FGMs. Recently, ZHANG et al [15] proposed a stochastic model of FGMs, and both random dynamic response and reliability were analytically obtained for a crack in an FGM layer between two dissimilar elastic half planes subjected to anti-plane loading.
Presently, this model is extended to the case of plane problem. Random dynamic analysis is performed for a crack in an FGM strip. The material properties of the strip vary randomly in the thickness direction, and the loadings applied on the crack faces are treated as stationary stochastic processes of time. In order to obtain the solution, the FGM strip is divided into several sub-strips, and the material properties of each sub-strip are reduced to random variables by an average method. Based on the use of Laplace and Fourier transforms, the boundary conditions are reduced to a set of singular integral equations, which can be solved by the Chebyshev polynomial expansions. The stress intensity factor history with its statistics is analytically derived. Numerical calculations are carried out to show the effects of the related parameters.
2 Formulation of problem
Consider an FGM strip with a crack as shown in Fig. 1. A set of Cartesian coordinates (x, y, z) is chosen such that the x-axis is directed along the crack line and y-axis is perpendicular to it. The crack faces are subjected to a pair of dynamic loadings σ(t), which can be described in a stochastic process:
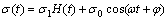(1)
where σ1 and σ0 are constants,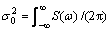 
dω; ω is a random variable and its probability density function is f(ω), 
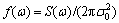; φ is a random variable uniformly distributed in [0, 2π] and independent of ω. Furthermore, suppose that S(ω) may be described by a low-pass white noise process as
(2)
where G0 and ω1 are constants.
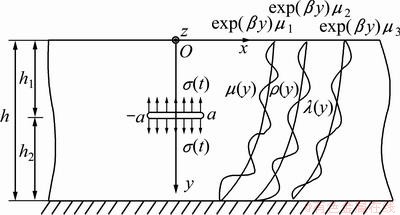
Fig. 1 Geometric configuration of problem
Elastic modulus, density and Lame constant of the FGM strip are assumed to be non-uniform fields of position in the y-direction, and take the form of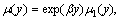 
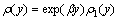and λ(y)= 
, respectively, where μ1(y), ρ1(y) and λ1(y) are assumed to be uniform fields, and β is a parameter.
The constitutive relations for the FGM strip can be expressed as
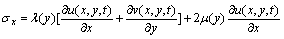(3a)
(3b)
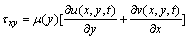(3c)
where σx, σy and σz are stress components;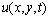 
and 
are displacements.
The equilibrium equations are given by
(4a)
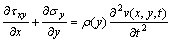(4b)
Substituting Eqs. (3a), (3b)and (3c) into Eqs. (4a) and (4b) results in the following governing equations:
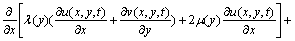
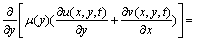
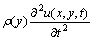(5a)
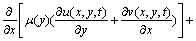
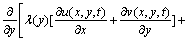
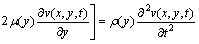(5b)
In order to obtain the solution, the FGM strip is divided into n sub-strips, and each sub-strip has the same thickness of L, as shown in Fig. 2.
Fig. 2 Division of FGM layer into sub-layers
The elastic modulus, density and Lame constant of the kth layer are averaged by
,
,
, 
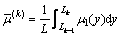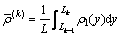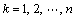(6)
Then, the material properties of each sub-strip are reduced to random variables.
Substituting Eq. (6) into Eqs. (5a) and (5b), we obtain
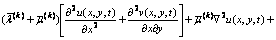
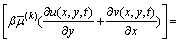
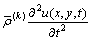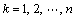, (7a)
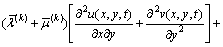
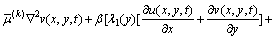
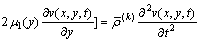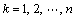, (7b)
The analysis is performed by using Laplace and Fourier transforms over time and space, respectively.
Define a Laplace transform pair by
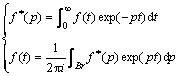(8)
where Br denotes the Bromwich path in transformed complex plane and p is the transform variable.
In the Laplace transform domain, the governing Eqs. (7a) and (7b) are converted to
,
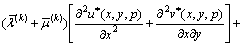
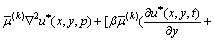
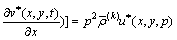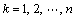(9a)
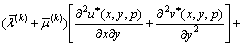
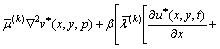
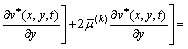
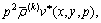
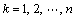(9b)
The boundary conditions can be expressed as
, 
, 
,
, 
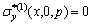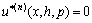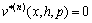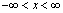(10a)
,
,
,
,
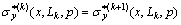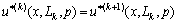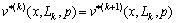(10b)
,
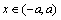(10c)
,
,
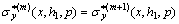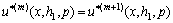(10d)
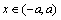, (10e)
,
, (10f)
3 Solution method
The general solutions for displacements in the Laplace transform domain are obtained by solving Eqs. (9a) and (9b) as follows:
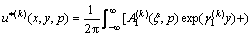
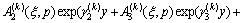
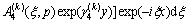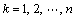, (11a)
,
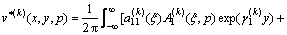
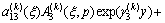
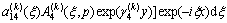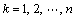(11b)
The stresses are found to be
,
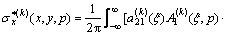
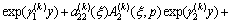
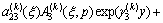
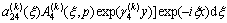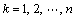(12a)
,
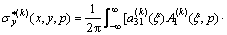
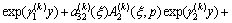
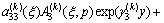
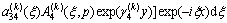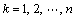(12b)
,
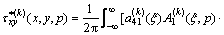
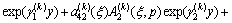
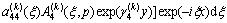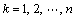(12c)
In the above formulations,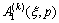 
and 
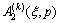
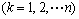are unknown functions to be solved. 
,
,
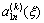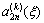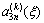and 
(n=1, 2, 3, 4) can be expressed by solving Eqs. (3), (4) and Eq. (9).
By substituting Eqs. (11) and (12) into the boundary conditions (10), we find
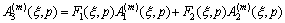(13a)
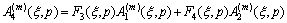(13b)
(13c)
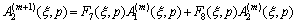(13d)
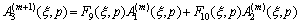(13e)
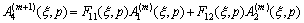(13f)
In the above,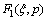 
-
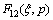can be derived by solving Eqs. (10-12).
We now introduce the following dislocation functions
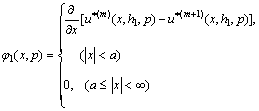(14a)
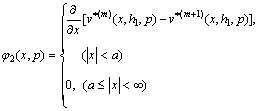(14b)
and these functions must satisfy
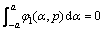(15a)
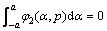(15b)
Substituting Eqs. (11) and (13) into Eqs. (14a) and (14b) yields
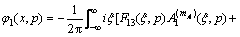
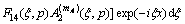(16a)
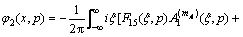
(16b)
where
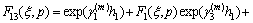
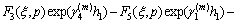
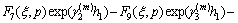
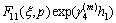
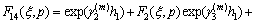
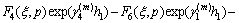
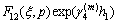
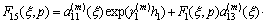
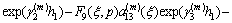
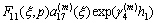
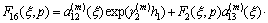
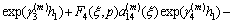
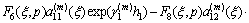
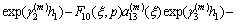
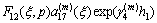
By using Eqs. (16a), (16b) and Fourier transforms, we have
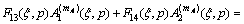
(17a)
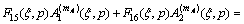
(17b)
From Eqs. (17a) and (17b), we have
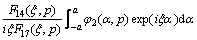(18a)
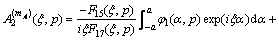
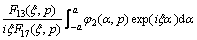(18b)
where
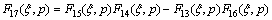
By substituting Eqs. (18a) and (18b) into Eqs. (10c) and (10e), we have
, 
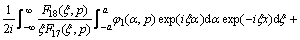
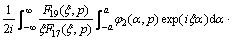
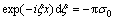(19a)
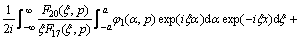
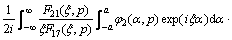
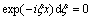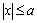, (19b)
where
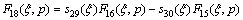
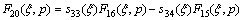
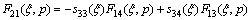
After performing the appropriate asymptotic analysis, the following results can be derived:
,
,
,
.
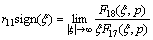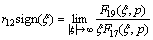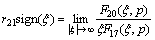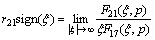From Eqs. (19a) and (19b), we obtain
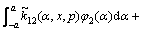
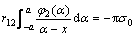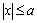, (20a)
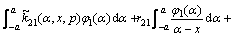
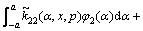
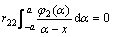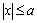, (20b)
where
,
,
,
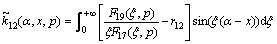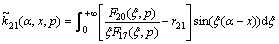Eqs. (20a) and (20b) are singular integral equations of the first kind. Their solutions include the well-known square-root singularity and can be expressed as
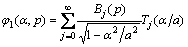(21a)
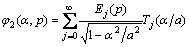(21b)
where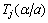 
is Chebyshev polynomials of the first kind, and 
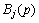and 
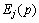are unknown constants. From the orthogonality conditions of Chebyshev polynomials, Eq. (14) leads to 
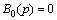and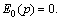 
Substituting Eqs. (21a) and (21b) into Eqs. (20a) and (20b), the following algebraic equations for 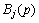and 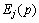are obtained:
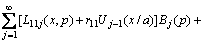
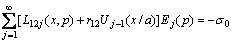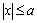, (22a)
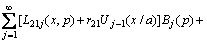
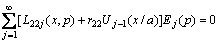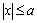, (22b)
where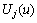 
represents Chebyshev polynomials of the second kind, and
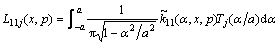
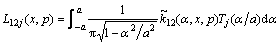
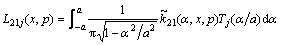
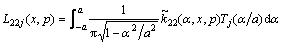
Truncating the Chebyshev polynomials in Eqs. (22a) and (22b) to the Nth term and assuming that Eqs. (22a) and (22b) are satisfied at N collocation points along the crack faces,
, 
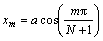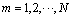(23)
we obtain the following linear algebraic equations:
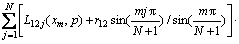
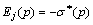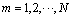, (24a)
, 
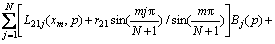
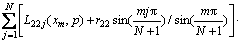
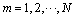(24b)
Then, the dynamic stress intensity factors can be evaluated using the following expressions:
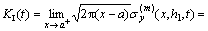
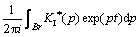(25)
where
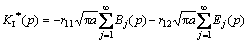
The mathematical expectation of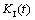 
is derived as
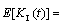
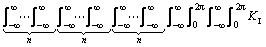
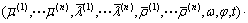
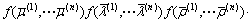
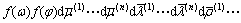
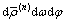(26)
The variance of 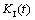becomes
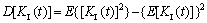(27)
4 Numerical results and discussion
Numerical calculations are carried out to show the influence of pertinent parameters on the dynamic stress intensity factor history. In the following, the FGM strip is assumed to be ceramics [16], with a thickness h=0.1 m. The mathematical expectation of elastic modulus, density and Lame constants are E[μ(y)]=11.811×1010exp(βy) N/m2, E[ρ(y)]=3900exp(βy) kg/m3, E[λ(y)]=13.8× 1010exp(βy) N/m2, and the standard deviations are 
4.7244×1010 N/m2, 
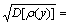1560 kg/m3, 
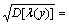5.52×1010exp(βy) N/m2, respectively. It is also assumed that 
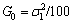and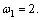 
The Durbin’s technique [17] is employed for the inversion of Laplace transform in Eq. (8).
4.1 Effect of crack length
Figures 3 and 4 show the effect of crack length on the mathematical expectation and standard deviation of normalized stress intensity factor history KI(t)/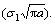
Here,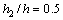 
, 
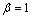. With the increase of crack length, both the mathematical expectation and standard deviation almost remain unchanged, indicating that the stress intensity factor history 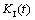is approximately proportional to the static solution 
.
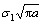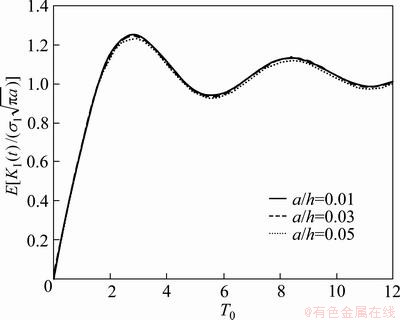
Fig. 3 Effect of crack length on mathematical expectation
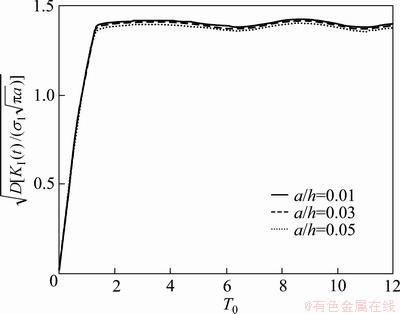
Fig. 4 Effect of crack length on standard deviation
4.2 Effect of parameter β
Figure 5 illustrates the effect of parameter β on the mathematical expectation of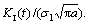 
The increase of this parameter leads to the increase of E[KI(t)/
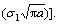At the same time, the standard deviation 
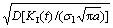becomes large (Fig. 6).
4.3 Effect of crack location
Finally, we examine the effect of crack location h2/h on the mathematical expectation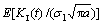 
(Fig. 7) and the standard deviation 
(Fig. 8). It is observed that the increase in the ratio 
leads to an obvious increase in both 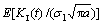and.
Fig. 5 Effect of parameter β on mathematical expectation
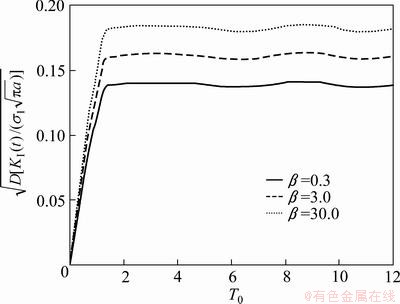
Fig. 6 Effect of parameter β on standard deviation
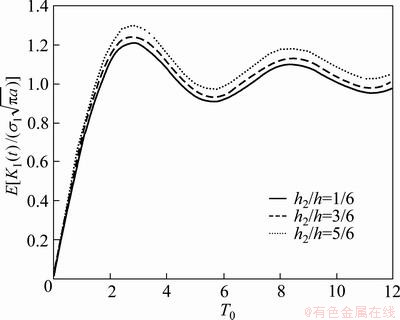
Fig. 7 Effect of crack location on mathematical expectation
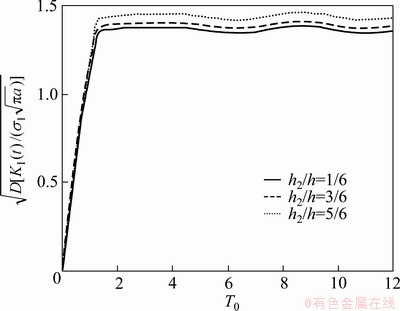
Fig. 8 Effect of crack location on standard deviation
5 Summary
Dynamic analysis is performed for a crack in an FGM strip subjected to plane loadings. The FGM strip is modeled as a random medium, while the transient loadings applied on the crack faces are treated as stochastic processes of time. To derive the solution of this problem, the FGM strip is divided into several sub-strips, and the material properties of each sub-strip are evaluated by the average method. Based on the use of Laplace and Fourier transforms, the boundary conditions are reduced to a set of singular integral equations, which are solved by the use of Chebyshev polynomials. The stress intensity factor history with its statistics is analytically obtained. From the numerical results, the following conclusions may be reached:
1) The normalized stress intensity factor history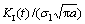 
is a non-stationary stochastic process of time, even if the loadings are stationary. Both the mathematical expectation and the standard deviation of the dynamic stress intensity factor history vary with the crack geometry.
2) The increase of parameter β leads to an increase of both mathematical expectation and standard deviation of normalized stress intensity factor history .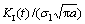
3) The increase in the ratio leads to an obvious increase in both the mathematical expectation and the standard deviation of .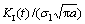
References
[1] MA L, WU L Z, GUO L C. Dynamic behavior of two collinear anti-plane shear cracks in a functionally graded layer bonded to dissimilar half planes [J]. Mechanics Research Communications, 2002, 29: 207-215.
[2] YUE Z Q, XIAO H T, THAM L G. Elliptical crack normal to functionally graded interface of bonded solids [J]. Theoretical and Applied Fracture Mechanics, 2004, 42: 227-248.
[3] MA L, WU L Z, ZHOU Z G. Dynamic stress intensity factors around two parallel cracks in a functionally graded layer bonded to dissimilar half-planes subjected to anti-plane incident harmonic stress waves [J]. International Journal of Engineering Science, 2004, 42: 187-202.
[4] LI X F, GUO S H. Effects of nonhomogeneity on dynamic stress intensity factors for an antiplane interface crack in a functionally graded material bonded to an elastic semi-strip [J]. Computational Materials Science, 2006, 38: 432-441.
[5] CHEN Y J, CHUE C H. Mode III crack problems of two bonded functionally graded strip with internal cracks [J]. International Journal of Solids and Structures, 2009, 46: 331-343.
[6] TORSHIZIAN M R, KARGAMOVIN M H. Anti-plane shear of an arbitrary oriented crack in a functionally graded strip bonded with two dissimilar half-planes [J]. Theoretical and Applied Fracture Mechanics, 2010, 54: 180-188.
[7] TAN M, MEGUID S A. Dynamic analysis of cracks perpendicular to bimaterial interfaces using a new singular finite element [J]. Finite Elements in Analysis and Design, 1996, 22: 69-83.
[8] WUNSCHE M, ZHANG C, SLADEK J. Transient dynamic analysis of interface cracks in layered anisotropic solids under impact loading [J]. International Journal of Fracture, 2009, 157: 131-147.
[9] HE X B, YANG H, ZHANG X M. Effect of fiber characteristics on fracture behavior of Cf/SiC composites [J]. Transactions of Nonferrous Metals Society of China, 2002, 12(1): 30-33.
[10] LOU B Y, YANG J L, LU C D, JIN J. Fracture behavior of B2-ordered iron aluminide with Mn addition [J]. Transactions of Nonferrous Metals Society of China, 2002, 12(5): 822-825.
[11] KOSTREVA M M, TALYBLY L, VIKTOROVA I V. Modeling of fatigue fracture under stationary stochastic loading conditions [J]. Applied Mathematics and Computation, 2007, 184(2): 874-879.
[12] LI X, YIN Z M, NIE B, ZHONG L, PAN Q L, JIANG F. High cycle fatigue and fracture behavior of 2124-T851 aluminum alloy [J]. Transactions of Nonferrous Metals Society of China, 2007, 17: 295-299.
[13] GAIDAI O, NAESS A, SOBCZYK K. The effect of fatigue-induced crack propagation on the stochastic dynamics of a nonlinear structure [J]. Probabilistic Engineering Mechanics, 2008, 23(4): 438-443.
[14] GAO L, CHEN R S, HAN E H. Fracture behavior of high strength Mg-Gd-Y-Zr magnesium alloy [J]. Transactions of Nonferrous Metals Society of China, 2010, 20: 1217-1221.
[15] ZHANG H Z, ZHAO X H, SU J X. Random dynamic response and reliability of a crack in a functionally graded material layer between two dissimilar elastic half planes [J]. Engineering Analysis with Boundary Elements, 2012, 36: 1560-1570.
[16] CAO X S, JIN F, JEON I. Calculation of propagation properties of Lamb waves in a functionally graded material (FGM) plate by power series technique [J]. NDT&E International, 2011, 44: 84-92.
[17] DURBIN F. Numerical inversion of Laplace transforms: An efficient improvement to Duber and Abate’s method [J]. The Computer Journal, 1974, 17: 371-376.
有裂纹的功能梯度材料板平面问题的随机动态响应
张会占1,2，赵晓华3，张嘉振1，周振功2
1. 中国商用飞机有限责任公司 北京民用飞机技术中心，北京 102211；
2. 哈尔滨工业大学 复合材料与结构研究所，哈尔滨 150001；
3. 汕头大学 土木工程系，汕头 515063
摘 要：研究有裂纹的功能梯度材料板平面问题的随机动态断裂，建立平面问题的随机模型。功能梯度材料的物理力学性能沿厚度方向的非均匀随机变化为沿厚度方向的随机场。作用在裂纹面上的动荷载为时间的平稳随机过程，裂纹与功能梯度材料面平行。通过分层法，将随机场的问题转化为多个随机变量的问题进行求解。利用积分变换方法和奇异积分方程技术，得到动态响应的解析形式和裂纹起始扩展的概率计算公式，分析了各参数(裂纹长度、随机场参数和裂纹位置)对动态应力强度因子的影响。结果表明：随着裂纹长度、随机场参数β以及裂纹位置比率h2/h的增大，应力强度因子的数学期望和标准方差均相应增大。
关键词：功能梯度材料；裂纹；动态响应；随机；应力强度因子
(Edited by CHEN Wei-ping)
Foundation item: Project (10972126) supported Partly by the National Natural Science Foundation of China; Project (06027215) supported by Natural Science Foundation of Guangdong Province, China
Corresponding author: ZHANG Hui-zhan; Tel: +86-10-57808721; Fax: +86-10-57808800; E-mail: zhanghuizhan@comac.cc
Abstract: In order to dynamically analyze a crack in a functionally graded materials layer for plane problem under dynamic loadings, a stochastic model is established for plane problem in which the material properties of the functionally graded materials layer vary randomly in the thickness direction, and the crack is parallel to the materials faces. A pair of dynamic loadings applied on the crack faces are treated as stationary stochastic processes of time. By dividing the functionally graded materials layer into several sub-layers, this problem is reduced to the analysis of laminated composites containing a crack, the material properties of each layer being random variables. A fundamental problem is constructed for the solution. Based on the use of Laplace and Fourier transforms, the boundary conditions are reduced to a set of singular integral equations, which can be solved by the Chebyshev polynomial expansions. The stress intensity factor history with its statistics is analytically derived. Numerical calculations are provided to show the effects of the related parameters. The results show that the increase of crack length, random field parameter β and crack location ratio h2/h leads to the increase of the mathematical expectation and standard deviation of normalized stress intensity factor history.
