- Abstract:
- 1 Introduction▲
- 2 Fractional derivat...▲
- 3 1D viscoelastic co...▲
- 4 Numerical solution...▲
- 5 Solution verificat...▲
- 6 Parameter analysis▲
- 7 Conclusions▲
- References
- Figure
- Figure 1 Spring-pot element
- Figure 2 Fractional derivative Merchant model
- Figure 3 Schematic diagram of calculation model with double-layered soil
- Figure 4 Comparison of numerical solutions in this paper with relevant literature:l
- Figure 5 Influence of i0 on consolidation behavior of double-layered soil:
- Figure 6 Influence of b on consolidation behavior of double-layered soil:
- Figure 7 Influence of R1 on consolidation behavior of double-layered soil:
- Figure 8 Influence of R2 on consolidation behavior of double-layered soil:
- Figure 9 Influence of V on consolidation behavior of double-layered soil:
- Figure 10 Influence of ɑ on consolidation behavior of double-layered soil:
- Figure 11 Influence of c on consolidation behavior of double-layered soil:

J. Cent. South Univ. (2021) 28: 284-296
DOI: https://doi.org/10.1007/s11771-021-4602-4
Analysis of one-dimensional rheological consolidation of double-layered soil with fractional derivative Merchant model and non-Darcian flow described by non-Newtonian index
CUI Peng-lu(崔鹏陆), LIU Zhong-yu(刘忠玉), ZHANG Jia-chao(张家超), FAN Zhi-cheng(范智铖)
School of Civil Engineering, Zhengzhou University, Zhengzhou 450001, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Abstract:
To further investigate the one-dimensional (1D) rheological consolidation mechanism of double-layered soil, the fractional derivative Merchant model (FDMM) and the non-Darcian flow model with the non-Newtonian index are respectively introduced to describe the deformation of viscoelastic soil and the flow of pore water in the process of consolidation. Accordingly, an 1D rheological consolidation equation of double-layered soil is obtained, and its numerical analysis is performed by the implicit finite difference method. In order to verify its validity, the numerical solutions by the present method for some simplified cases are compared with the results in the related literature. Then, the influence of the revelent parameters on the rheological consolidation of double-layered soil are investigated. Numerical results indicate that the parameters of non-Darcian flow and FDMM of the first soil layer greatly influence the consolidation rate of double-layered soil. As the decrease of relative compressibility or the increase of relative permeability between the lower soil and the upper soil, the dissipation rate of excess pore water pressure and the settlement rate of the ground will be accelerated. Increasing the relative thickness of soil layer with high permeability or low compressibility will also accelerate the consolidation rate of double-layered soil.
Key words:
Cite this article as:
CUI Peng-lu, LIU Zhong-yu, ZHANG Jia-chao, FAN Zhi-cheng. Analysis of one-dimensional rheological consolidation of double-layered soil with fractional derivative Merchant model and non-Darcian flow described by non-Newtonian index [J]. Journal of Central South University, 2021, 28(1): 284-296.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-021-4602-41 Introduction
Rheological property is an important engineering property of soil, which affects the consolidation and deformation of saturated soft clay ground. Therefore, since the establishment of Terzaghi’s 1D consolidation theory, many scholars have carried out a series of studies on the viscoelastic consolidation of soft soil ground [1-7], but the above studies mainly focus on 1D rheological consolidation problem of single-layer soil. As is known to all, layered soil is another important feature of soil structure. Double-layered soil, as the simplest layered soil, its 1D rheological consolidation problem has gradually attracted scholars’s attention. LAN et al [8] used the Merchant model to reflect the linear rheological properties of soil, deduced the one-dimensional consolidation equation of layered soil, and analyzed the influence of rheological parameters on the consolidation behavior by taking the double-layered soil as an example. Then, ZHENG et al [9], based on Kelvin model, studied the one-dimensional consolidation problem of layered and saturated viscoelastic soil with impeded boundaries under cyclic loading. LIU et al [10] further studied the viscoelastic consolidation problem of double- layered soil based on the generalized Voigt rheological model. Nevertheless, in the past few decades, many scholars [11-13] pointed out that the fractional derivative model (FDM) is more suitable for describing the viscoelastic mechanical of various real materials. Among them, GEMANT [13] verified the applicability of the FDM to viscoelastic soil through experiments, which also paved the way for the application of FDM in the field of geotechnical engineering. Subsequently, some scholars [14-19] have respectively introduced modified Kelvin’s, Burger’s and Merchant’s models based on fractional derivatives to fit these oedometric or triaxial rheological experimental data of different soft soils, and all of which have achieved a better agreement to the field settlement observations. LIU et al [20, 21], and WANG et al [22, 23] have also introduced fractional derivative Merchant model (FDMM) or Kelvin model to study single-layer consolidation of viscoelastic soil. Up to now, the 1D consolidation of viscoelastic soil with double-layered soil has been seldom simulated using a FDM.
In addition, it should be pointed out that at present, most of the studies on 1D consolidation or rheological consolidation theory of double-layered soil assume that the flow of water obeys Darcy’s law. However, many permeability tests and field observation data [24-35] showed that the water flow in fine-grained soil may deviate from Darcy’s law under low hydraulic gradient. HANSBO [24] took the lead in calling this phenomenon as non-Darcian flow, and proposed a non-Darcian flow model with power function and threshold hydraulic gradient. LI et al [36, 37] had also considered this non-Darcian flow model to derive the 1D consolidation difference solution of double-layered soil. However, the mathematical description of Hansbo’s flow model is expressed by a piecewise function, so its form is slightly more complicated and its section interval is also difficult to determine. It is believed that the deviation of water flow from Darcy’s law under low gradient may be caused by the characteristics of non-Newtonian fluid in soil. Therefore, SWARTZENDRUBER [38] proposed an empirical relation expressed by non-Newtonian index to describe the non-Darcian flow, and its mathematical expression is:
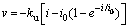 (1)
(1)
where v is the flow velocity; i is the hydraulic gradient; ku and i0 are called the permeability coefficient and the non-Newtonian index, respectively. It is can be seen that Eq. (1) is reduced to Darcy’s law when i0=0.
Compared with Hansbo’s flow model, the parameters of Swartzendruber’s flow model described by Eq. (1) is less, and it can also fit well with the permeability tests reported by HANSBO [24]. LI et al [39] and LIU et al [21, 40] introduced Eq. (1) to simulate the non-Darcy water flow through the pores, and preliminarily analyzed the influence of its parameters on the consolidation behavior of single-layered ground and ideal sand-drained ground.
To further investigate the applicability of FDM in the consolidation theory of double-layered soil, we introduced the FDMM based on Caputo’s definition of fractional derivative [41] to characterize the viscoelastic behavior of soil. Simultaneously, considering Swartzendruber’s flow equation (Eq. (1)) to depict the flow in the pore of soil in the process of consolidation on the basis of LIU et al [21, 40]. Then, the 1D viscoelastic consolidation equation of saturated double-layered soil is rederived, and the implicit finite difference method is used to find its numerical solution. On this basis, the influence of the parameters of Swartzendruber’s flow model and FDMM on 1D viscoelastic consolidation behavior of double- layered soil are studied.
2 Fractional derivative Merchant model
A spring-pot element, as shown in Figure 1, is defined by KOELLER [42], and it represents a relation between stress σ and strain ε at time t as follows:
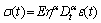 , 0≤α≤1 (2)
, 0≤α≤1 (2)
where η=F/E stands for the relaxation time or creep time of the viscoelastic body; E and F are the elastic modulus and viscosity coefficient, respectively; 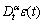 stands for the fractional derivative of Caputo’s definition [42], which is defined by:
stands for the fractional derivative of Caputo’s definition [42], which is defined by:
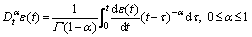 (3)
(3)
where t is the time after loading; Γ(·) is the Gamma function; α stands for the fractional order. When α=0, the element can be simplified into a spring element with elastic modulus E, while it can be reduced into a dashpot element with viscosity coefficient F when α=1. Thus, when α varies from 0 to 1, the element can describe the mechanical behavior of the viscoelastic body.
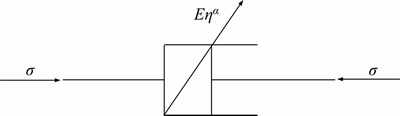
Figure 1 Spring-pot element
The FDMM, as shown in Figure 2, is composed of an independent spring element in a series with a fractional derivative Kelvin model (FDKM) which consists of the other spring-pot element in parallel connection with a Hookean spring.
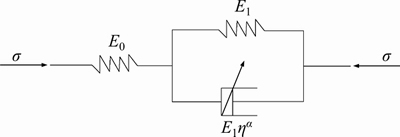
Figure 2 Fractional derivative Merchant model
Assume that the total stress and the total strain for the FDMM are σ and ε, respectively, while the stresses for the independent spring element and the FDKM in series are σ0 and σ1, respectively, and their corresponding strains are ε0 and ε1, respectively. Then the relationships between stress and strain for the spring element and for the FDKM in series can respectively be expressed as:
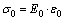 (4)
(4)
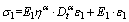 (5)
(5)
where E0 and E1 are the elastic moduli represented by the spring element and the FDKM, respectively.
The serial connection of the spring element and the FDKM gives:
 (6)
(6)
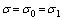 (7)
(7)
The constitutive relationship of the FDMM cannot easily be written as explicit formulation but can easily be as the Laplace transform:
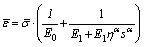 (8)
(8)
where s is a Laplace variable; 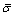 and
and 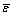 are the Laplace transforms of σ and ε, respectively. And the Laplace inverse transform of Eq. (8) gives the creep compliance of the FDMM:
are the Laplace transforms of σ and ε, respectively. And the Laplace inverse transform of Eq. (8) gives the creep compliance of the FDMM:
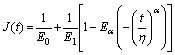 (9)
(9)
where 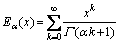 is the single parameter Mittag-Leffler function. It can be acknowledged that, if α=1,
is the single parameter Mittag-Leffler function. It can be acknowledged that, if α=1, 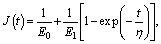 i.e., the FDMM reduces to the integer-derivative or classic Merchant model.
i.e., the FDMM reduces to the integer-derivative or classic Merchant model.
Then under the condition of small strain, the constitutive equation of viscoelastic material based on fractional derivative can be expressed as:
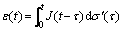 (10)
(10)
where σ′ is the vertical effective stress.
3 1D viscoelastic consolidation equation
Calculation model of double-layered soil is shown in Figure 3.
As shown in Figure 3, the ground consists of two soil layers, with a pervious upper boundary and an impervious lower boundary. The thickness,permeability coefficient, non-Newton index and model parameters of the upper and lower soil layers are respectively as hβ, kuβ, i0β and αβ, Fβ, E0β, E1β (β=1, 2). It is assumed that the ground has been completely consolidated under the action of self-weight stress, and the top surface of the ground is abruptly applied with an infinitely wide uniform load of p0 at a time. Other basic assumptions follow the Terzaghi’s 1D consolidation, and the non- Darcian flow with non-Newtonian index and the FDMM are used to describe the water flow in the consolidation process and the viscoelastic deformation of the soil skeleton, and the parameters of each model are constant. The pore water pressure at time t and depth z is uβ (z, t); the flow velocity is vβ (z, t); and the vertical strain is εβ (z, t). According to the continuity condition that the change of water quantity in a unit cell should be equal to the volume change of the unit cell, the following can be obtained:
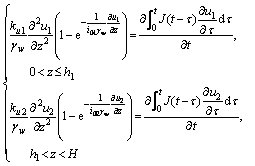 (11)
(11)
The initial conditions of the subject are:
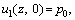
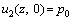 (12)
(12)
The boundary conditions are as follows:

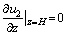 (13)
(13)
The continuous conditions of pore pressure and flow velocity between different soil layers can be expressed as:
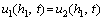 (14)
(14)
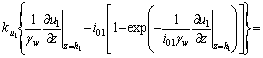
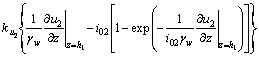 (15)
(15)
To simplify the process of calculation, the dimensionless variables are introduced as follows:

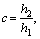
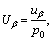
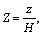
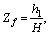
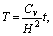
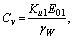


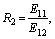
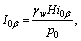
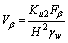 (16)
(16)
where β=1 or 2, similarly hereinafter.
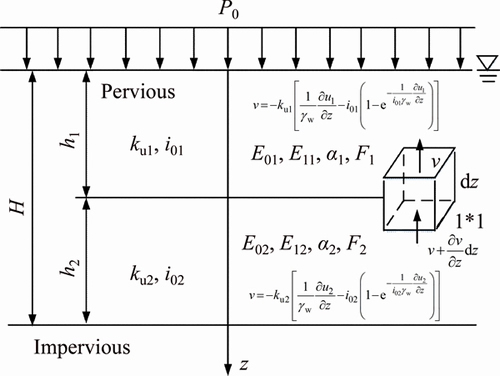
Figure 3 Schematic diagram of calculation model with double-layered soil
Then, Eqs. (11)-(15) can be turned into:
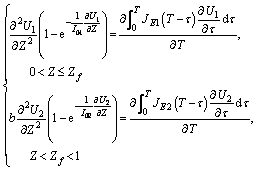 (17)
(17)
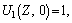
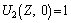 (18)
(18)
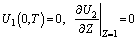 (19)
(19)
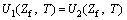 (20)
(20)
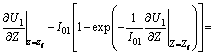
 (21)
(21)
where
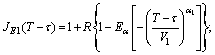
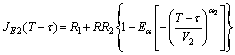 .
.
4 Numerical solution of consolidation equation
The implicit finite difference scheme is introduced to solve Eq. (17), that is, the double- layered soil is uniformly dispersed into the K-1 layer with the thickness △z along the direction of Z axis, and the node number is from 1 to K, wherein the node number of upper soil layer (0-Zf) is from 1 to K1. In addition, the time step is taken as △T to discretize the time axis. Thus, the difference grid is formed in the spatial domain and the time domain, and the governing Eq. (17) can be discretized as:
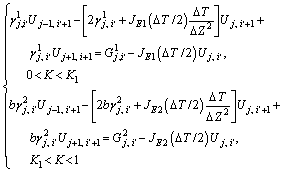 (22)
(22)
where superscript indicates soil layer 1 or 2; subscript j, i′ respectively represent the spatial node and the time node, i′=1, 2, …, N; for the j-th soil layer, hydraulic gradient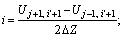 the remaining parameters are respectively expressed as follows:
the remaining parameters are respectively expressed as follows:
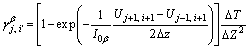 ;
;
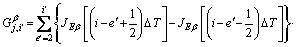
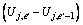
Equation (18) is discretized as follows:
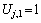 (23)
(23)
For the boundary condition of Eq. (19), the virtual node K+1 is introduced, the boundary point is processed in a similar way to LI et al [39]. Then Eq. (19) is discretized as:
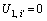 (24)
(24)
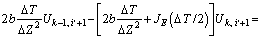
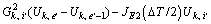 (25)
(25)
The continuity condition of Eq. (21) is:
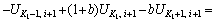
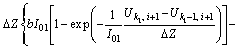
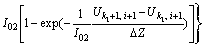 (26)
(26)
Thus, Eqs. (22)-(26) compose a closed system of equations, which can be obtained by the iterative method. After calculating the pore-water pressure U, the average degree of consolidation Up defined by the pore-water pressure and consolidation degree US defined by deformation can be further obtained:
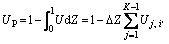 (27)
(27)
 (28)
(28)
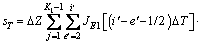
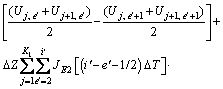
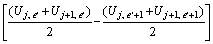 (29)
(29)
where sT and s∞ are respectively the consolidation settlement and the final settlement of the ground at time T.
Particularly, when the parameters of the double-layered soil are the same, the corresponding expression is degraded to one-layer soil.
5 Solution verification
When the parameters of the double-layered soil are completely consistent, it can be degraded into a single-layer ground consolidation problem. LIU et al [21] have discussed in detail the special case of single-layer ground consolidation of this paper. In order to verify the effectiveness of this algorithm, some examples from Ref. [21] are calculated here. The specific material parameters and calculation results are presented in Figure 4(a). In addition, when I01=I02=0 and R=R2=0, the research topic in this paper degenerates into the elastic consolidation problem of double-layered soil under Darcy’s law. LI et al [36] have given the difference calculation results in this case with Crank-Nicolson difference scheme. Here, the same calculation parameters as those in Ref. [36] were selected by this method, and the numerical algorithm in this paper is further verified and the corresponding calculation results are also shown in Figure 4(b). As can be seen from Figure 4, the results in this paper are quite consistent with the results of the example in Refs. [21, 36], which indicates that the numerical algorithm in this paper is reasonable and effective.
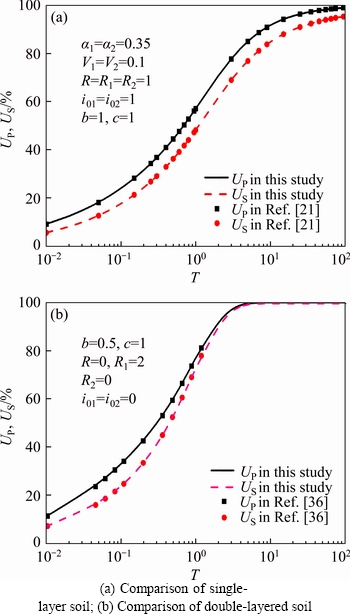
Figure 4 Comparison of numerical solutions in this paper with relevant literature:l
6 Parameter analysis
In order to facilitate the analysis, the influence of single factor variable on each parameter is discussed here.
6.1 Influence of dimensionless variable I0
LIU et al [21] and LI et al [39] pointed out the influence of non-Darcian flow on consolidation behavior when analyzing the single-layer consolidation or rheological consolidation problem described by non-Newton index. The larger the dimensionless variable I0 is, the slower the consolidation rate of single-layer ground will be. Figure 5 shows the influence curves of the dimensionless variable I0 on consolidation degree UPand US in double-layered soil versus time factor T. It can be seen from the two figures that when the dimensionless variable I0 in the upper soil layer is the same and the I0 in the lower soil layer increases from 1 to 5, the consolidation degree of the two different definitions only decreases slightly, and almost coincides in the early and middle stages of consolidation. On the contrary, when the I0 in the lower soil layer is the same ones, the I0 in the upper soil layer increases from 1 to 5, and the consolidation degree of the two definitions slows down significantly. That is to say, under the condition of single drainage on the upper surface, the upper seepage parameters play a decisive role in influencing the consolidation behavior of the double-layered soil, and the seepage parameters in the lower soil layer have a small influence on the consolidation behavior, which is also consistent with LI’s analysis [36] of the influence of exponential flow on the consolidation behavior of double-layered soil. In addition, the transverse comparison of Figures 5(a) and (b) under the same parameters shows that, at the same time, the consolidation degree US in terms of deformation is less than the consolidation degree UP in terms of pore pressure, that is, the settlement of ground in double-layered soil is slower than the overall dissipation of pore water pressure, which is still consistent with the conclusion of single-layer consolidation theory [21].
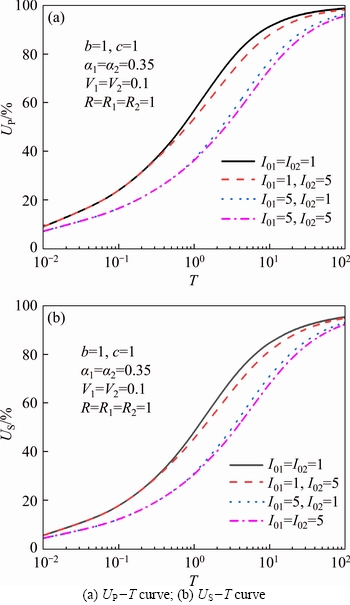
Figure 5 Influence of i0 on consolidation behavior of double-layered soil:
6.2 Influence of relative permeability of soil layer
b=ku2/ku1 is the ratio of permeability coefficient of the lower soil layer to the upper soil layer. In order to investigate the effect of relative permeability on consolidation behavior of double- layered soil, Figure 6 shows the relationships between consolidation degree UP and US with time factor under different b values. It can be observed from Figure 6 that, on the premise that other parameters remain unchanged, with the increase of the relative ratio of permeability coefficient between the lower soil layer and the upper soil layer (i.e., the greater the b value), the greater the consolidation degree UP and the US are, the smaller the relative ratio of the permeability coefficient between the lower soil layer and the upper soil layer is (i.e., the smaller the b value), the smaller the consolidation degree UP and US is. That is, the overall dissipation rate of pore water pressure and the settlement rate of the ground accelerate with the increase of b value, and slow down with the decrease of b value. This is also consistent with the law of LI’s analysis [36] of the influence of relative permeability on double-layered soil.
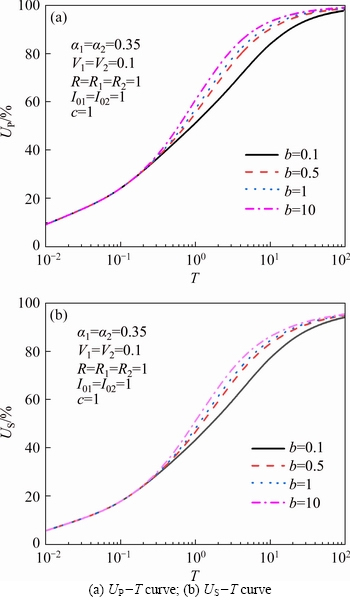
Figure 6 Influence of b on consolidation behavior of double-layered soil:
6.3 Influence of FDMM’s parameters
6.3.1 For modular ratio R1 and R2
R1=E01/E02 is the ratio of independent spring modulus of the upper soil layer to lower soil layer; R2=E11/E12 is the ratio of the series spring of the fractional kelvin body of the upper soil layer to lower soil layer. Figures 7 and 8 show the influence curves of R1 and R2 on the average consolidation degree UP and US of double-layered soil, respectively. It can be seen from Figure 7 that UP and US decrease with the increase of R1, i.e., with the increase of relative compressibility between the lower soil layer and upper soil layer, the overall dissipation rate of the pore pressure and the settlement rate of the ground decrease accordingly. It can also be seen from Figure 7(a) that the consolidation degree UP in terms of pore pressure does not change R1 value at the early stage of consolidation, but changes significantly during the middle and late stages of consolidation, which indicates that the overall dissipation of pore pressure in the early stage of consolidation is almost not changed with the relative compressibility of the upper soil layer and lower soil layer. This is because under the condition of single drainage of the upper surface, the overall dissipation of the pore pressure at the initial stage of consolidation is mainly concentrated on the upper soil layer. So under this scenario, the total dissipation of the pore pressure is mainly determined by the properties of the upper soil layer, and the properties of the lower soil have little influence which can almost be ignored [8]. The influence curves of R2 on consolidation behavior of double-layered soil in Figure 8 are similar to those of R1, except that the influence curves of consolidation degree UP and US change more obviously with the change of R2 value. That is to say, R2 value has a greater influence on consolidation behavior than R1.
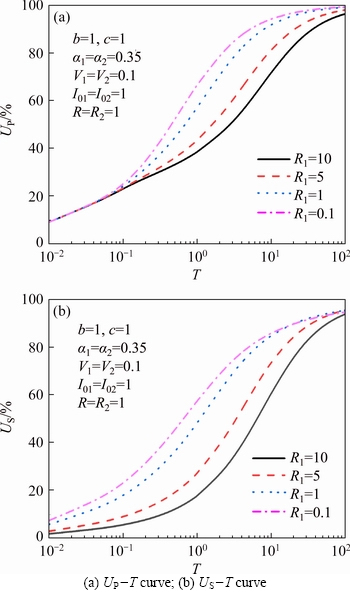
Figure 7 Influence of R1 on consolidation behavior of double-layered soil:

Figure 8 Influence of R2 on consolidation behavior of double-layered soil:
6.3.2 For dimensionless coefficient V and fraction order a
In order to investigate the effect of viscosity coefficient V on consolidation behavior of double- layered soil, Figure 9 shows the curves of consolidation degree UP and US with time T when V in upper and lower soil layers is taken as 1 and 0.01, respectively. It can be seen from Figure 9(a) that the change of V of the upper and lower soil layers has little effect on UP. When the viscosity coefficient V of the upper soil layer is fixed and the parameter V of the lower soil layer is changed, the curves almost overlap. On the contrary, when the viscosity coefficient V of the lower soil layer is fixed, the parameter V of the upper layer is changed, and the curves change more obviously, which indicates that the viscosity coefficient V of the upper layer of the double-layered soil plays a dominant role in the overall dissipation of pore pressure. In Figure 9(b), the influence of viscosity coefficient V on US is similar to that of UP, i.e., the influence of viscosity coefficient of the upper soil layer plays a decisive role on the settlement rate of the double-layered soil, while the viscosity parameters of the lower layer play a smaller role. The difference is that the viscosity coefficient V has a greater influence on the settlement rate of double-layered soil. In addition, when the V value of the upper and lower soil layers is the same or larger, the US decreases more and more obviously in the whole consolidation process with time, while the UP increases slightly at the initial and the middle stages of the consolidation. But with the development of time, the UP is slightly reduced in the later stage of consolidation. For example, when V1=V2=1, the time factors for UP reaching 50% and 95% are T50=0.63, T90=8.9, respectively. When V1=V2=0.01, T50 increases to 0.75 and T90 decreases to 8.8, which is similar to the effect of viscosity coefficient on consolidation properties of single layer soil [21].
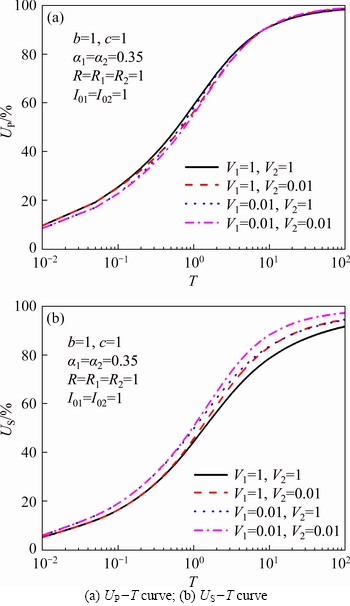
Figure 9 Influence of V on consolidation behavior of double-layered soil:
The influence curves of fractional order ɑ on consolidation behavior of double-layered soil are given in Figure 10. As can be seen from Figure 10, similar to the influence of viscosity coefficient V on double-layered soil, the influence of fractional order ɑ on UP is less sensitive, and the influence on US is greater. And the parameter of the upper soil layer greatly influences the consolidation character of the double-layered soil. It can be furtherly seen from Figure 10(b) that the influence of fractional order ɑ on the settlement rate of the double-layered soil is mainly reflected at the middle and late stages of consolidation. Under the same parameter, the smaller the fractional order ɑ, the slower the consolidation rate of the foundation. This conclusion is also consistent with LIU’s analysis [21] of the influence of fractional order ɑ on the consolidation process of one-layer soil.
6.4 Influence of relative thickness of soil layer
Figure 11 shows the effect of relative thickness c on consolidation behavior when the compressibility or the permeability of the upper and lower soil layers is the same. When b=0.5, R1=1, it indicates that the upper and lower soil layers in the double-layered soil have the same compressibility, while the upper soil layer has a high permeability and the lower soil layer has a low permeability; when b=1, R1=2, it indicates that the upper and lower soil layers in the double-layered soil have the same permeability, and the upper soil layer has a small compressibility and the lower soil layer has a large compressibility. From Figures 11(a)-(d), it can be seen that with the increase of soil thickness with high permeability or low compressibility (the decrease of c value), the dissipation rate of pore water pressure and the settlement rate of ground will gradually accelerate, which means that in actual engineering, replacing soft soil with high- permeability and low-compressibility materials, not only increases the bearing capacity of ground, but also accelerates the consolidation of soil. This is also consistent with the conclusion in Ref. [36] which analyzes the effect of relative thickness on consolidation properties when considering non-Darcian flow.
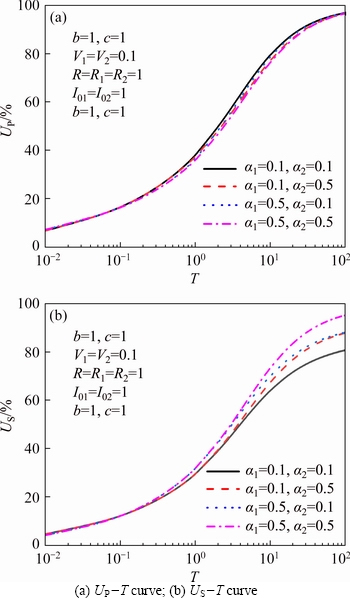
Figure 10 Influence of ɑ on consolidation behavior of double-layered soil:
7 Conclusions
The FDMM and the non-Darcian flow with non-Newtonian index are introduced to simulate the deformation of saturated viscoelastic soil and the water flow through the pores respectively, the 1D rheological consolidation equation of saturated double-layered soil is obtained. Through the comparison of relevant literatures, the rationality of the algorithm in this paper is verified, and the following conclusions are drawn:
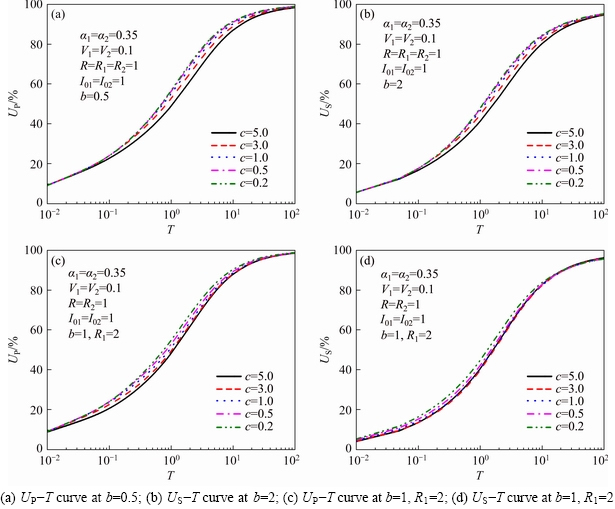
Figure 11 Influence of c on consolidation behavior of double-layered soil:
1) The larger the dimensionless variable I0 is, the slower the consolidation rate of double-layered soil is. In particular, under the condition of single drainage on the upper surface, the I0 value of the first soil layer greatly influences the consolidation rate of double-layered soil, while the influence of I0 value of the lower soil layer is small. That is to say, for doubled-layered soil, the influence of flow parameter in the drainage surface layer on consolidation behavior plays a decisive role, and this rule is also applicable to the parameters of FDMM.
2) The relative compressibility and relative permeability of the upper and lower soil layers greatly influence the consolidation rate of the double-layered soil. Under the premise that the relative thickness of the double-layered soil is the same, the greater the relative permeability (the larger b) or the lower the relative compressibility (the smaller R1 or R2) between the lower and upper soil layer, the faster the consolidation rate of the double-layered soil will be, and R2 has a greater influence on the consolidation behavior than R1. In addition, when the two layers of the double-layered soil maintain the same relative permeability or compressibility, with the increase of the thickness of the soil layer with good permeability or low compressibility, the dissipation rate of pore pressure and ground settlement rate in the foundation will also be accelerated.
3) The influence of fractional order ɑ and viscosity coefficient V on UP is relatively small, but the influence on US is greater. At the middle and late stages of consolidation, with the decrease of ɑ or the increase of V, the consolidation degree US increases obviously, i.e., the influence of ɑ and V on the settlement rate of double-layered soil is mainly reflected at the middle and late stages of consolidation.
Nomenclature
b, c
Ratio of permeability coefficient and thickness of the lower soil layer to the upper soil layer, respectively
Cv
Coefficient of consolidation
E
Elastic modulus
E0β, E1β
Modulus of independent spring and the series spring of the fractional kelvin body of the first soil layer, respectively, β=1, 2
Eɑ(x)
Mittag-Leffler function
Fβ
Viscosity coefficient
H
Total thickness of double-layered soil
hβ
Thickness of the upper and lower soil layer when β=1 or 2, respectively
i’, j
Time node and spatial node, respectively
i0β, kuβ
Non-Newtonian index and permeability coefficient, respectively
I0β, V0β, T,
U, Z
Dimensionless variables of i0, F, t, u and z respectively, as shown in Eq. (1)
J
Creep compliance
P0
Vertical distributed load
s
Variable of Laplace transformation
UP, US
Degree of consolidation in terms of pore pressure and deformation, respectively
R1
Ratio of independent spring modulus of the upper soil layer to lower soil layer
R2
Ratio of the series spring of the fractional kelvin body of the upper soil layer to lower soil layer
v
Flow velocity
αβ
Fractional order
η
Viscous time
γw
Unit weight of water
ε
Vertical strain
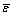
Laplace transformation of ε
σ′
Effective stress
σ
Vertical stress
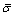
Laplace transformation of σ
Contributors
The overarching research goals were developed by CUI Peng-lu, LIU Zhong-yu, ZHANG Jia-chao, FAN Zhi-cheng, LIU Zhong-yu contributed to the conception of the paper. ZHANG Jia-chao, FAN Zhi-cheng participated in the analysis of relevant calculated results. The initial draft of the manuscript was written by CUI Peng-lu, LIU Zhong-yu. All authors replied to reviewers’ comments and revised the final version.
Conflict of interest
CUI Peng-lu, LIU Zhong-yu, ZHANG Jia-chao, FAN Zhi-cheng declare that they have no conflict of interest.
References
[1] TAYLOR D W, MERCHANT W. A theory of clay consolidation accounting for secondary compression [J]. Journal of Mathematics and Physics, 1940, 19(1-4): 167-185. DOI: 10.1002/sapm1940191167.
[2] CHEN Zong-ji. Secondary time effects and consolidation of clays [J]. Science in China: Ser. A, 1958, 11: 1060–1075. (in Chinese)
[3] CAI Yuan-qiang, XU Chang-jie, YUAN Hai-ming. One- dimensional consolidation of layered and visco-elastic soils under arbitrary loading [J]. Applied Mathematics and Mechanics, 2001, 22(3): 353-360. DOI: 10.3321/j.issn: 1000-0887.2001.03.011.
[4] LO K Y. Secondary compression of clays [J]. Journal of Soil Mechanics and Foundation, ASCE, 1961, 87(4): 39–46.
[5] ZHAO Wei-bing. One-dimensional soil consolidation theory of saturated soil based on generalized Voigt model and its application [J]. Chinese Journal of Geotechnical Engineering, 1989, 11(5): 78-85. (in Chinese)
[6] LI Chuan-xun, XIE Kang-he, WANG Kun. Analysis of 1D consolidation with non-Darcian flow described by exponent and threshold gradient [J]. Journal of Zhejiang University: Science A, 2010, 11(9): 656-667. DOI: 10.1631/jzus. A0900787.
[7] LI Chuan-xun, WANG Chang-jian, LU Meng-meng, LU Jian-fei, XIE Kang-he. One-dimensional large-strain consolidation of soft clay with non-Darcian flow and nonlinear compression and permeability of soil [J]. Journal of Central South University, 2017, 24(4): 967-976. DOI: 10.1007/s11771-017-3499-4.
[8] LAN Liu-he, XIE Kang-he, ZHENG Hui. The analysis of linear rheological consolidation of layered soils [C]// The Academic Conference Proceedings of 5th Conference on Geomechanics and Engineering in Zhejiang Province. Beijing: China Water Power Press, Intellectual Property Press, 2002: 18-22. (in Chinese)
[9] ZHENG Zao-feng, CAI Yuan-qiang, XU Chang-jie, ZHAN Hong. One-dimensional consolidation of layered and visco- elastic ground under arbitrary loading with impeded boundaries [J]. Journal of Zhejiang University: Engineering Science, 2005, 39(8): 1234-1237, 1272. DOI:10.3785/j.issn. 1008-973X.2005.08.029. (in Chinese)
[10] LIU Jia-cai, ZHAO Wei-bing, ZAI Jin-min, WANG Xu-dong. Analysis of one-dimensional consolidation of double-layered viscoelastic ground [J]. Rock and Soil Mechanics, 2007, 28(4): 743-746, 752. DOI: 10.3969/j.issn.1000-7598.2007. 04.021. (in Chinese)
[11] PODKUBNY I. Fractional differential equations [M]. California: Academic Press, 1999.
[12] MULLER S, KASTNER M, BRUMMUND J, ULBRICHT V. A nonlinear fractional viscoelastic material model for polymers [J]. Computational Materials Science, 2011, 50(10): 2938-2949. DOI: 10.1016/j.commatsci.2011.05.011.
[13] GEMANT A. A method of analyzing experimental results obtained from elasto-viscous bodies [J]. Physics, 1936, 7(8): 311-317. DOI: 10.1063/1.1745400.
[14] LIU Lin-chao, YAN Qi-fang, SUN Hai-zhong. Study on model of rheological property of soft clay [J]. Rock and Soil Mechanics, 2006, 27(S1): 214-217. DOI: 10.16285/j.rsm. 2006.s1.069. (in Chinese)
[15] HE Li-jun, KONG Ling-wei, WU Wen-jun, ZHANG Xian-wei, CAI Yu. A description of creep model for soft soil with fractional derivative [J]. Rock and Soil Mechanics, 2011, 32(S1): 239-249. DOI: 10.16285/j.rsm.2011.s2.022.
[16] ZHU Hong-hu, ZHANG Cheng-cheng, MEI Guo-xiong, SHI Bin, GAO Lei. Prediction of one-dimensional compression behavior of Nansha clay using fractional derivatives [J]. Marine Georesources & Geotechnology, 2017, 35(5): 688-697. DOI: 10.1080/10 64119X.2016.1217958.
[17] YIN De-shun, LI Yan-qing, WU Hao, DUAN Xiao-meng. Fractional description of mechanical property evolution of soft soils during creep [J]. Water Science and Engineering, 2013, 6(4): 446-455. DOI: 10.3882/j.issn.1674-2370.2013. 04.008.
[18] LUO Qing-zi, CHEN Xiao-ping, WANG Sheng, HUANG Jing-wu. An experimental study of time-dependent deformation behaviour of soft soil and its empirical model [J]. Rock and Soil Mechanics, 2016, 37(1): 66-75. DOI: 10.16285/j.rsm.2016.01.008. (in Chinese)
[19] ZHANG Chun-xiao, XIAO Hong-bin, BAO Jia-miao, YIN Ya-hu, YIN Duo-lin. Stress relaxation model of expansive soils based on fractional calculus [J]. Rock and Soil Mechanics, 2018, 39(5): 1747–1752, 1760. DOI: 10.16285/ j.rsm.2016.2371. (in Chinese)
[20] LIU Zhong-yu, YANG Qiang. One-dimensional rheological consolidation analysis of saturated clay using fractional order Kelvin’s model [J]. Rock and Soil Mechanics, 2017, 38(12): 3680-3687. DOI: 10.16285/j.rsm.2017.12.036. (in Chinese)
[21] LIU Zhong-yu, CUI Peng-lu, ZHENG Zhan-lei, XIA Yang- yang, ZHANG Jia-chao. Analysis of one-dimensional rheological consolidation with non-Darcy flow described by non-Newtonian index and fractional-order Merchant’s model [J]. Rock and Soil Mechanics, 2019, 40(6): 2029–2038. DOI: 10.16285/j.rsm.2018.1085. (in Chinese)
[22] WANG Lei, SUN De-an, LI Pei-chao, XIE Yi. Semi- analytical solution for one-dimensional consolidation of fractional derivative viscoelastic saturated soils [J]. Computers and Geotechnics, 2017, 83: 30-39. DOI: 10.16285/j.rsm.2017.11.020.
[23] WANG Lei, LI Lin-zhong, XU Yong-fu, XIA Xiao-he, SUN De-an. Analysis of one-dimensional consolidation of fractional viscoelastic saturated soils with semi-permeable boundary [J]. Rock and Soil Mechanics, 2018, 39(11): 4142-4148. DOI:10.16285/j.rsm.2017.0659. (in Chinese)
[24] HANSBO S. Consolidation of clay, with special reference to influence of vertical sand drains [D]. Swedish Geotechnical Institute, 1960.
[25] HANSBO S. Aspects of vertical drain design: Darcian or non-Darcian flow [J]. Géotechnique, 1997, 47(5): 983-992. DOI: 10.1680/geot.1997.47.5.983.
[26] HANSBO S. Consolidation equation valid for both Darcian and non-Darcian flow [J]. Géotechnique, 2001, 51(1): 51-54. DOI: 10.1680/geot.51.1.51.39357.
[27] ING T C, XIAOYAN N. Coupled consolidation theory with non-Darcian flow [J]. Computers and Geotechnics, 2002, 29(3): 169-209. DOI: 10.1016/s0266-352x(01)00022-2.
[28] HANSBO S. Deviation from Darcy’s law observed in one- dimensional consolidation [J]. Géotechnique, 2003, 53(6): 601-605. DOI: 10.1680/geot.2003.53.6.601.
[29] DENG Ying-er, XIE He-ping, HUANG Run-qiu, LIU Ci-qun. Law of nonlinear flow in saturated clays and radial consolidation [J]. Applied Mathematics and Mechanics, 2007, 28(11): 1427-1436. DOI: 10.1007/s10483-007-1102-7.
[30] KIANFAR K, INDRARATNA B, RUJIKIATKAMJORN C. Radial consolidation model incorporating the effects of vacuum preloading and non-Darcian flow [J]. Géotechnique, 2013, 63(12): 1060-1073. DOI: 10.1680/geot.1.P.163.
[31] MISHRA A, PATRA N R. Long-term response of consolidating soft clays around a pile considering non-Darcian flow [J]. International Journal of Geomechanics, 2019, 19(6): 04019040. DOI: 10.1061/(ASCE)GM.1943- 5622.0001392.
[32] CHEN Xu, TANG Chu-nan, YU Jin, ZHOU Jian-feng, CAI Yan-yan. Experimental investigation on deformation characteristics and permeability evolution of rock under confining pressure unloading conditions [J]. Journal of Central South University, 2018, 25(8): 1987-2001. DOI: 10.1007/s11771-018-3889-2.
[33] ZHAO Xu-dong, GONG Wen-hui. Model for large strain consolidation with non-Darcian flow described by a flow exponent and threshold gradient [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2019, 43(14): 2251-2269. DOI: 10.1002/nag.2946.
[34] LIU Zhong-yu, ZHANG Jia-chao, DUAN Shu-qian, XIA Yang-yang, CUI Peng-lu. A consolidation modelling algorithm based on the unified hardening constitutive relation and Hansbo’s flow rule [J]. Computers and Geotechnics, 2020, 117: 103233. DOI: 10.1016/j.compgeo. 2019.103233.
[35] LIU Zhong-yu, XIA Yang-yang, SHI Ming-sheng, ZHANG Jia-chao, ZHU Xin-mu. Numerical simulation and experiment study on the characteristics of non-darcian flow and rheological consolidation of saturated clay [J]. Water, 2019, 11(7): 1385. DOI: 10.3390/w11071385.
[36] LI Chuan-xun, XIE Kang-he, LU Meng-meng, MIAO Yong-hong, XIE Gui-hua. Analysis of one-dimensional consolidation of double-layered soil with exponential flow considering time-dependent loading [J]. Rock and Soil Mechanics, 2012, 33(5): 1565-1571. DOI: 10.16285/j.rsm. 2011.01.045. (in Chinese)
[37] LI Chuan-xun, XIE Kang-he, HU An-feng, HU Bai-xiang. One-dimensional consolidation of double-layered soil with non-Darcian flow described by exponent and threshold gradient [J]. Journal of Central South University, 2012, 19(2): 562-571. DOI:10.1007/sl1771-012-1040-3.
[38] SWARTZENDRUBER D. Modification of Darcy's law for the flow of water in soils [J]. Soil Science, 1962, 93(1): 22-29. DOI: 10.1097/00010694-196201000-00005.
[39] LI Chuan-xun, XIE Kang-he, LU Meng-meng, WANG Kun. Analysis of one-dimensional consolidation with non-Darcy flow described by non-Newtonian index [J]. Rock and Soil Mechanics, 2011, 32(1): 281-287. DOI: 10.16285/j.rsm. 2011.01.045. (in Chinese)
[40] LIU Zhong-yu,CUI Peng-lu, ZHANG Jia-chao, XIA Yang- yang. Analysis of consolidation of ideal sand-well ground with non-Darcian flow described by non-Newtonian index and fractional-derivative Merchant model [J]. Mathematical Problem in Engineering, 2019: 5359076. DOI: 10.1155/ 2019/5359076.
[41] CAPUTO M. Elasticità e dissipazione [M]. Bologna: Zani-chelli., 1969.
[42] KOELLER R C. Applications of fractional calculus to the theory of viscoelasticity [J]. Journal of Applied Mechanics, 1984, 51(2): 299-307. DOI: 10.1115/1.3167616.
(Edited by ZHENG Yu-tong)
中文导读
基于非牛顿指数渗流和分数阶Merchant模型的双层地基一维流变固结分析
摘要:为了进一步深入探讨饱和黏土双层地基一维固结机理,引入Koeller定义的弹壶元件修正Merchant模型描述饱和黏土的黏弹性变形,引入非牛顿指数渗流模型描述固结过程中的非Darcy渗流,推导出一个新的饱和黏性土双层地基一维流变固结方程,并利用隐式差分格式进行数值求解。通过文献对比,验证了本文数值算法的有效性。探讨了非牛顿指数渗流模型参数以及分数阶Merchant流变模型参数对双层地基一维流变固结过程的影响。结果表明,在单面排水条件下,上层中渗流参数和模型参数对固结速率的影响起决定作用,且随着下层土与上层土的相对压缩性的降低或相对渗透性的增加,地基孔压的消散速率和沉降速率都会加快;增大渗透性高或压缩性低的土层相对厚度,也会加快双层地基的固结速率。另外,非牛顿指数的增大会延缓双层地基中的孔压消散,使得沉降发展变慢。
关键词:双层地基;流变固结;分数阶导数;非达西渗流;非牛顿指数;有限差分法;黏弹性
Foundation item: Project(51578511) supported by the National Natural Science Foundation of China
Received date: 2019-09-19; Accepted date: 2020-03-13
Corresponding author: LIU Zhong-yu, PhD, Professor; Tel: +86-13939066332; E-mail: zhyliu@zzu.edu.cn; ORCID: https://orcid.org/ 0000-0002-1127-6569
Abstract: To further investigate the one-dimensional (1D) rheological consolidation mechanism of double-layered soil, the fractional derivative Merchant model (FDMM) and the non-Darcian flow model with the non-Newtonian index are respectively introduced to describe the deformation of viscoelastic soil and the flow of pore water in the process of consolidation. Accordingly, an 1D rheological consolidation equation of double-layered soil is obtained, and its numerical analysis is performed by the implicit finite difference method. In order to verify its validity, the numerical solutions by the present method for some simplified cases are compared with the results in the related literature. Then, the influence of the revelent parameters on the rheological consolidation of double-layered soil are investigated. Numerical results indicate that the parameters of non-Darcian flow and FDMM of the first soil layer greatly influence the consolidation rate of double-layered soil. As the decrease of relative compressibility or the increase of relative permeability between the lower soil and the upper soil, the dissipation rate of excess pore water pressure and the settlement rate of the ground will be accelerated. Increasing the relative thickness of soil layer with high permeability or low compressibility will also accelerate the consolidation rate of double-layered soil.
- Analysis of one-dimensional rheological consolidation of double-layered soil with fractional derivative Merchant model and non-Darcian flow described by non-Newtonian index


