裂纹扩展过程模拟的无网格流形MSIM方法
苏锋1, 2, 3,蔡永昌3
(1. 中国电建集团华东勘测设计研究院有限公司,浙江 杭州,310014;
2. 浙江中科依泰斯卡岩石工程研发有限公司,浙江 杭州,310014;
3. 同济大学 地下建筑与工程系,上海,200092)
摘 要:
网格流形MSIM方法来进行裂纹扩展过程的模拟分析。该方法利用单位分解法和有限覆盖技术来构造插值函数,该插值函数的建立不受域内不连续面的影响,可较好地求解裂纹扩展问题;此外,该插值函数还具有高阶完备性、一致性,且可以在需要的节点处具备delta属性,能够方便、准确地施加各种边界条件。与通常的无网格方法相比,该方法由于采用了有限覆盖技术,试函数的构造不受域内不连续面的影响,克服了传统的无网格方法在处理不连续问题时由于采用光线法所遇到的困难;与数值流形方法相比,该方法用一系列节点的影响域来建立有限覆盖和单位分解函数,具有无网格方法的特性,摆脱了传统数值流形方法中在处理复杂非连续问题时网格所带来的困难,且其覆盖系统的生成远比数值流形方法中覆盖系统的生成简单。数值算例结果表明本文方法用于追踪复杂应力状态下裂纹扩展过程的正确性和有效性。
关键词:
无网格方法;数值流形方法;单位分解法;有限覆盖理论;裂纹扩展;Shepard函数;
中图分类号:TU411 文献标志码:A 文章编号:1672-7207(2014)07-2360-09
Simulation of crack propagation by MSIM method
SU Feng1, 2, 3, CAI Yongchang3
(1. PowerChina Huadong Engineering Corporation, Hangzhou 310014, China;
2. HydroChina Itasca R&D Center, Hangzhou 310014, China;
3. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China)
Abstract: A newly proposed meshless Shepard interpolation method (MSIM) interpolation was employed for the simulation of crack growth. The shape functions in this method were formed by the partition of unity and the finite cover technology, so the shape functions are not affected by discontinuous domains and crack problems can be more properly treated. This MSIM shape function possesses three distinguished features: the interpolation property, the arbitrarily high order consistency, and satisfy delta property at any desired node. Thus the essential boundary conditions can be treated as easily as they are in finite element method (FEM). Compared with the conventional meshless methods, the shape functions are not influenced by the discontinuities in the solution domain because finite cover technology is used. Compared with the numerical manifold method, the finite covers and the partition of unity functions are formed by using the influence domains of a series of nodes with advantages over the mesh-based numerical manifold method, and the algorithm for the finite covers of the MSIM is much simpler than the popular finite cover method based on the finite meshes. Numerical examples indicate the advantages and the accuracy of the present method for the analysis of cracks propagation.
Key words: meshless method; numerical manifold method; partition of unity; finite cover theory; crack propagation; Shepard function
在长期的实践中,人们已经逐渐意识到岩石或混凝土等结构的安全与稳定与其微裂纹萌生、扩展、演化到宏观裂纹的形成和最终的断裂破坏有着密不可分的关系[1-3],因此近二三十年来,研究带裂纹的材料和构件中裂纹扩展条件和扩展规律的断裂力学分析方法,在理论研究与工程应用中得到了越来越多的关注。尽管断裂力学在工程应用中取得了一定的成就[4-6],但在断裂机理及其与环境之间的关系研究方面还很不完善,尤其对于复杂的多裂纹之间的相互作用等问题的研究更是欠缺。对于具有复杂几何形状和边界条件的岩土工程问题,采用解析方法进行裂纹扩展及演化过程的分析在目前的理论和技术水平下是不现实的,也是不可能的,在实际应用中主要采用数值计算方法来进行分析和求解。以有限元为代表的数值方法用特殊单元(如Goodman单元)来模拟少数几条裂纹,或用奇异等参元、改变形函数的内嵌裂缝的非连续单元等方法来解决裂纹尖端的应力奇异性[7-9]。但是,对于具有动边界的裂纹扩展问题,有限元类基于网格的方法需要不断地调整或重建网格,其过程繁琐,分析难度大,且严重降低了解的精度。无网格方法由于在插值时只需要离散结点,突破了单元和网格对插值的限制,从而得到了众多学者的关注与重视。在无网格方法里,裂纹可以沿任意方向动态扩展,且易于推广到三维,比基于网格的方法具有明显的优势[10-14]。但是,作为一种新兴的数值方法,无网格方法大多还存在着形函数的求导及计算复杂、本质边界条件难以施加、计算时间长、影响半径的选取对计算结果影响大等缺点,并且该法在构造试函数时受域内不连续的影响,在求解断裂力学问题时均采用光线法(如可视、衍射准则)来处理域内的不连续问题,对于复杂的多条裂纹问题可能会由于插值点不足导致试函数难以建立、产生数值解的不稳定等问题[15-17]。数值流形方法采用分离的数学覆盖和物理覆盖来统一处理连续和非连续的力学问题,通过引入数学与物理双重网格和有限覆盖技术使得连续变形分析与非连续变形分析得到了统一[18-20]。数值流形方法在进行裂纹扩展模拟时其数学网格可保持不变,只需调整流形单元的物理覆盖编号,故比有限元方法更适合于裂纹扩展模拟,但是,在处理动边界的裂纹扩展问题时,数值流形方法的覆盖系统生成算法十分复杂[21],严重地限制了其进一步应用及向三维的扩展。近年来,有些学者将无网格方法和流形方法相结合所提出的无网格流形类方法,借鉴无网格插值技术和流形方法的有限覆盖技术,较好地克服了原有流形方法的覆盖系统生成受制于网格的缺 点[22-24]。但目前的无网格流形方法均无一例外地采用了滑动最小二乘插值(MLS)作为覆盖权函数,其计算复杂、计算时间长和本质边界条件难以施加等困难也得到了继承。本文作者采用新发展的基于单位分解法和有限覆盖技术建立起来的无网格流形MSIM方法(meshless Shepard interpolation method,简称MSIM)[25]来克服或减少目前无网格流形方法所面临的主要困难。该方法兼具无网格摆脱单元限制的优点和流形方法的有限覆盖技术,可处理任意复杂的不连续问题;且该方法在位移边界节点处的局部近似函数采用了Shepard-最小二乘(SLS)[26]插值技术,满足了delta属性,能够方便、准确地施加本质边界条件,其计算和求导过程也比基于MLS插值的无网格流形方法简 单。在本文中采用J积分法计算混合裂纹的应力强度因子。
1 无网格流形MSIM插值函数
在无网格流形MSIM方法中,位移试函数的建立是基于单位分解概念构造。如图1所示的任意分析区域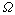 ,共离散成了N个结点。对于每一个节点i,它的圆形覆盖子域可表示为
,共离散成了N个结点。对于每一个节点i,它的圆形覆盖子域可表示为
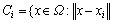 ≤
≤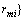 (1)
(1)
其中:rmi为子覆盖Ci的覆盖半径;节点i处的位移变量可表示为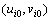 。
。
对于一个给定的计算点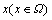 ,基于单位分解函数的概念,其位移近似函数(以
,基于单位分解函数的概念,其位移近似函数(以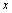 方向的位移
方向的位移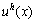 为例)可由
为例)可由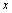 周围的n个邻接结点定义如下:
周围的n个邻接结点定义如下:
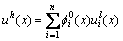 (2)
(2)
式中:n为包含在计算点x影响域内的节点个数;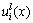 为在结点i的局部影响域上定义的局部近似函数。在MSIM方法中,对于任意形状的二维离散域区域,局部近似函数是在位于离散域位移边界上的节点处和离散域其他位置(统称为离散域内部)的节点处分别建立的,
为在结点i的局部影响域上定义的局部近似函数。在MSIM方法中,对于任意形状的二维离散域区域,局部近似函数是在位于离散域位移边界上的节点处和离散域其他位置(统称为离散域内部)的节点处分别建立的,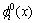 是和覆盖
是和覆盖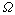 相关的单位分解函数,取Shepard形函数(也称0阶MLS形函数),即
相关的单位分解函数,取Shepard形函数(也称0阶MLS形函数),即
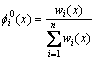 (3)
(3)
式中: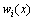 是结点i相关的权函数。
是结点i相关的权函数。
若在x=xi处奇异,则Shepard形函数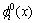 满足
满足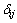 条件,则文中采用如下形式的奇异权函数[27]:
条件,则文中采用如下形式的奇异权函数[27]:
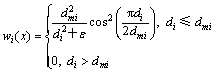 (4)
(4)
其中: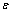 为一个很小的实数如 10-15,其作用是为了避免结点处权函数计算的数值奇异性;
为一个很小的实数如 10-15,其作用是为了避免结点处权函数计算的数值奇异性;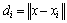 表示计算点x与结点xi之间的距离。
表示计算点x与结点xi之间的距离。
对于任意结点i,其对应于式(1)的局部近似函数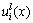 定义为如下形式:
定义为如下形式:
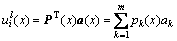 (5)
(5)
其中: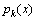 是形如
是形如 的多项式基函数;m为基函数的数量;ai为系数。
的多项式基函数;m为基函数的数量;ai为系数。
下面以二维空间的二次基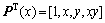 为例来阐述无网格流形MSIM的插值试函数推导过程。
为例来阐述无网格流形MSIM的插值试函数推导过程。
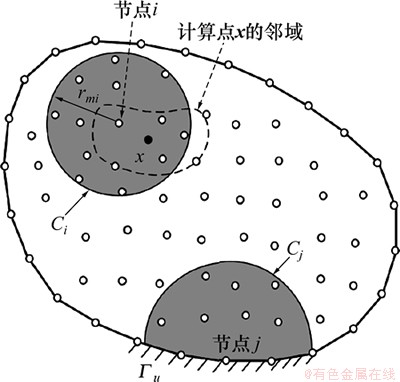
图1 任意形状的分析区域
Fig. 1 Arbitrary discrete domain
1.1 当节点位于二维离散域内部时局部近似函数的建立
如图1所示,节点i位于二维离散域内部(不在位移边界上),则节点i处的局部近似函数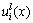 (以x方向的位移为例)可表示为
(以x方向的位移为例)可表示为
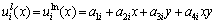 (6)
(6)
当计算点位于节点i处时,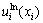 在节点i处,必须满足
在节点i处,必须满足
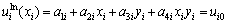 (7)
(7)
由此推出
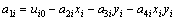 (8)
(8)
将式(5)代入式(3)可得
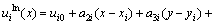
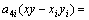
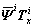 (9)
(9)
其中:
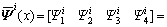
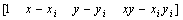 (10)
(10)
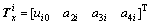 (11)
(11)
根据同样的原理,可得y方向的位移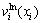 :
:
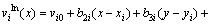
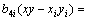
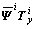 (12)
(12)
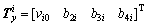 (13)
(13)
式(9)和式(12)可以被写为
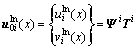 (14)
(14)
其中:
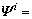
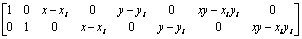 (15)
(15)
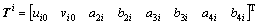 (16)
(16)
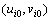 为节点i处的位移;系数
为节点i处的位移;系数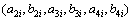 为节点i处的多余自由度,通过式(9)可得
为节点i处的多余自由度,通过式(9)可得
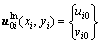 (17)
(17)
1.2 当节点位于二维离散域位移边界上时局部近似函数的建立
如图1所示,节点j表示为二维离散域位移边界上的节点,Cj表示节点j的影响域,假设在j点影响域Cj中有M个节点;对结点j影响范围内的任意点x,其局部近似位移函数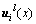 (以x方向的位移为例)可定义为
(以x方向的位移为例)可定义为
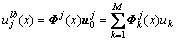 (18)
(18)
其中:
 (19)
(19)
 (20)
(20)
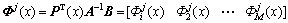 (21)
(21)
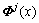 为结点k(k=1, …, M)相关的最小二乘形函数;
为结点k(k=1, …, M)相关的最小二乘形函数;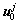 是节点函数值向量;M为处于结点j影响范围
是节点函数值向量;M为处于结点j影响范围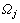 内的结点个数;
内的结点个数;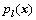 为多项式基函数。
为多项式基函数。
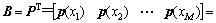
 (22)
(22)
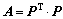 (23)
(23)
可以看出式(19)中最小二乘插值函数不满足在节点j处的插值条件,即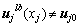 ,为了能够方便地施加本质边界条件,对式(18)作如下修正:
,为了能够方便地施加本质边界条件,对式(18)作如下修正:
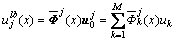 (24)
(24)
其中:
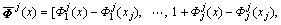
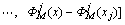 (25)
(25)
 为节点j的坐标。从式(25)中可以得出修改后的函数满足
为节点j的坐标。从式(25)中可以得出修改后的函数满足
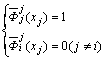 (26)
(26)
故有
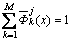 (27)
(27)
从而强制其满足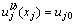
根据同样的原理,可得y方向的位移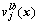
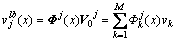 (28)
(28)
其中:
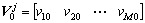 (29)
(29)
式(24)和式(28)可写为
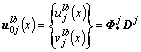 (30)
(30)
其中:
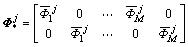 (31)
(31)
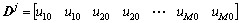 (32)
(32)
由此可见:位于本质边界上的节点j,其子域内仅有代表节点位移的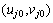 2个未知量;位于区域内部的节点i,有
2个未知量;位于区域内部的节点i,有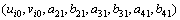 8个未知量,其中
8个未知量,其中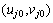 代表节点i处的位移,而多余的6个自由度用来模拟逼近函数。
代表节点i处的位移,而多余的6个自由度用来模拟逼近函数。
将式(14)和式(30)代入式(2)得
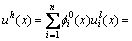
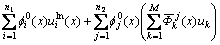 (33)
(33)
其中: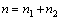 为包含在计算点x影响域内的节点个数,n1代表位于离散域
为包含在计算点x影响域内的节点个数,n1代表位于离散域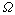 内部的点的个数,n2代表区域
内部的点的个数,n2代表区域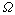 内位于离散域边界上的点的个数,可以验证本文的MSIM插值函数满足Kronecher-delta特性、近似一致性和高阶完备性[25]。
内位于离散域边界上的点的个数,可以验证本文的MSIM插值函数满足Kronecher-delta特性、近似一致性和高阶完备性[25]。
1.3 非连续情况下MSIM插值试函数的建立
在无网格流形MSIM方法中,对于不连续的模拟,是通过增加1个或多个子覆盖得以实现的;当不连续穿过节点数学覆盖时,节点数学覆盖被不连续分解成2个或多个子覆盖,试函数在每一子覆盖内都是连续的。
对于任意分析区域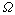 ,共离散成N个结点,每个节点的圆形覆盖域可表示为
,共离散成N个结点,每个节点的圆形覆盖域可表示为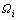 (i=1, 2, …, N);对于一个任意给定的计算点
(i=1, 2, …, N);对于一个任意给定的计算点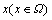 ,假设在其插值域内的节点i的覆盖被域内不连续分解成了k个子覆盖,此时计算点x的位移近似函数表示为
,假设在其插值域内的节点i的覆盖被域内不连续分解成了k个子覆盖,此时计算点x的位移近似函数表示为
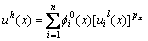 (px=1, 2, …, M) (34)
(px=1, 2, …, M) (34)
其中:n为包含在计算点x插值域内的节点个数,m为节点i的覆盖被不连续分割成的子覆盖的个数;px为计算点x所在节点i的第k个子覆盖中的编号。
如图2所示的计算点x插值域内包含节点i、节点j、节点k和节点d 4个节点(图2(a)),其中节点i被裂纹1和裂纹2切割成了4个子覆盖(图2(b)),计算点x位于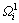 子覆盖中,即在式(34)中节点i处取px=1;节点j被裂纹线1割成了2个子覆盖(图2(c)),计算点x位于
子覆盖中,即在式(34)中节点i处取px=1;节点j被裂纹线1割成了2个子覆盖(图2(c)),计算点x位于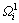 子覆盖中,即在式(34)中节点j处取px=1;由于节点k(图2(d))和节点d处(图2(e))的覆盖没有被裂纹切割,故图2(a)所示计算点x的插值函数可表示为:
子覆盖中,即在式(34)中节点j处取px=1;由于节点k(图2(d))和节点d处(图2(e))的覆盖没有被裂纹切割,故图2(a)所示计算点x的插值函数可表示为:
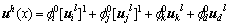 (35)
(35)
无网格流形MSIM方法的优势首先在于可以解决传统的无网格方法在处理复杂的多条裂纹问题时,由于采用光线法(如可视、衍射准则)可能会由于插值点不足导致试函数难以建立,产生数值解的不稳定的问题;如图3所示,在无网格计算中,由于2条裂纹线1和裂纹线2的影响,计算点x的插值节点在限制在两条裂纹线之间,当裂纹线夹角取很小值时,计算点x就可能由于插值点不足导致试函数难以建立。其次无网格流形MSIM方法也解决了基于MLS的无网格流形方法位移边界条件难以施加的问题。
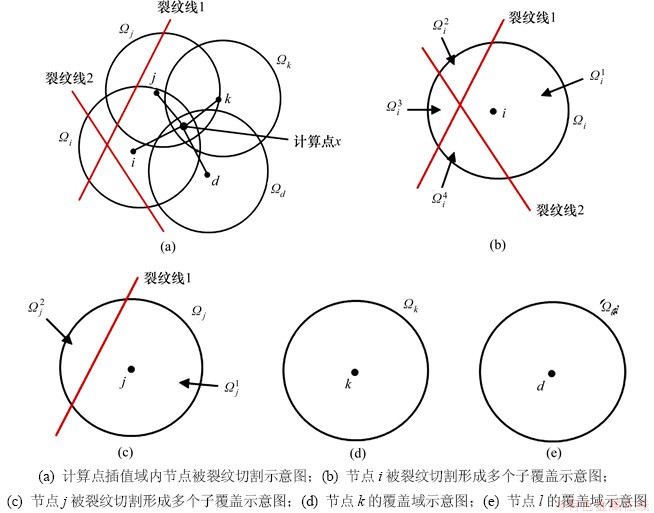
图2 无网格流形MSIM子覆盖生成示意图
Fig. 2 Illustrations of basic concepts of MSIM
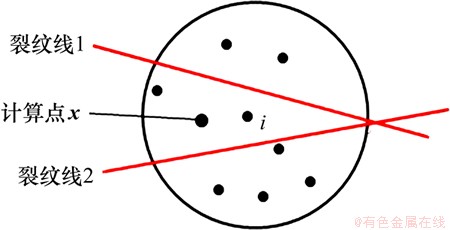
图3 无网格方法裂纹线附近节点插值示意图
Fig. 3 Meshless interpolation points for multiple crack problem
2 离散控制方程与裂纹扩展准则
考虑二维弹性静力求解问题,可以给出MSIM要求的控制方程的能量泛函的积分(弱)形式可表示为
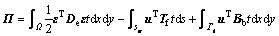 (36)
(36)
其中: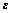 为应变量;t为二维体的厚度;Bb为体积力向量;Tf为面力向量;De为弹性矩阵。
为应变量;t为二维体的厚度;Bb为体积力向量;Tf为面力向量;De为弹性矩阵。
采用最小势能原理最终可导出如下离散控制方 程[28]:
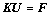 (37)
(37)
式中:K为刚度矩阵;F为荷载矩阵。则
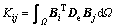 (i=1, 2, 3, …; j=1, 2, 3, …) (38)
(i=1, 2, 3, …; j=1, 2, 3, …) (38)
式中:Bi为应变子矩阵。
研究裂纹体结构中裂纹的扩展时,合理断裂准则的确定以及应力强度因子的精确计算是十分重要的。目前计算复杂几何形状和复杂载荷下的混合型裂纹应力强度因子主要有围线积分法、边界配置法虚拟裂纹法和J 积分法[29]等,而复合裂纹的断裂准则有最大周向应力准则、最大能量释放率准则和应变能密度因子准则等。本文采用J 积分法来计算混合型裂纹的应力强度因子,采用最大周向应力准则来确定裂纹的开裂角,并认为裂尖沿着最大周向应力的法向扩展,其计算公式为
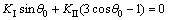 (39)
(39)
由式(39)求出了裂纹的开裂角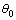 后,即可得
后,即可得 圆周上的最大周向应力为
圆周上的最大周向应力为
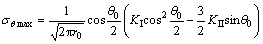 (40)
(40)
式(40)中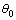 的方向是由前段裂缝延伸线逆时针方向算起,如图4所示。
的方向是由前段裂缝延伸线逆时针方向算起,如图4所示。
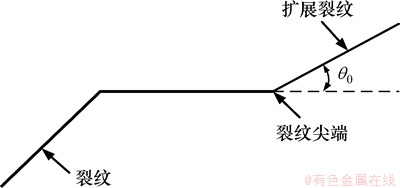
图4 裂缝尖端扩展方向角
Fig. 4 Crack propagation angle
根据周向应力理论的第二个假设可建立相应的断裂准则
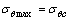 (41)
(41)
其中: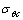 为最大周向应力的临界值,它可以通过Ⅰ型裂纹的断裂韧度
为最大周向应力的临界值,它可以通过Ⅰ型裂纹的断裂韧度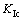 来确定。
来确定。
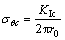 (42)
(42)
此外,裂纹扩展步长的选择也很重要,在本研究中采用0.15a i (a i为初始裂纹长度,i为裂纹个数)作为裂纹扩展步长[30],以取得较满意的计算结果。
3 算例验证
本文进行裂纹扩展过程模拟分析的MSIM无网格流形程序采用Matlab编制,并利用如下算例对其理论和方法进行测试和验证。
3.1 有限平板分叉裂纹应力强度因子分析
图5所示为1个有限平板分叉裂纹示意图,图6所示为无网格模型图。计算中取板长和宽均为2W=10 m,为了消除板边界对裂纹应力强度影子的影响,取a/W=0.1即a=0.5 m,板的上下方对称分布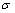 =1 Pa的均布拉力。材料弹性模量E=1 kPa,泊松比取μ=0.3;取
=1 Pa的均布拉力。材料弹性模量E=1 kPa,泊松比取μ=0.3;取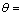 45°,b/a=0.1,b/a=0.3,b/a=0.5,b/a=0.7等几种情况,分析了A和B两点的应力强度因子计算值。该问题中A和B 2点的应力强度因子解析解由Chen等[31]推导得出:
45°,b/a=0.1,b/a=0.3,b/a=0.5,b/a=0.7等几种情况,分析了A和B两点的应力强度因子计算值。该问题中A和B 2点的应力强度因子解析解由Chen等[31]推导得出:
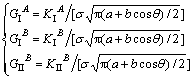 (43)
(43)
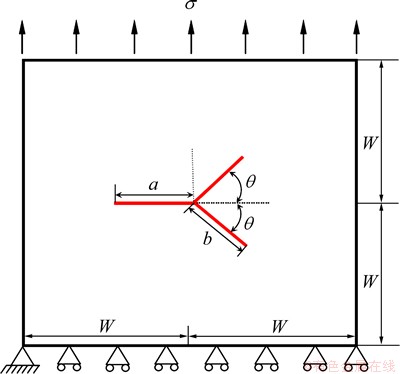
图5 有限平板分叉裂纹示意图
Fig. 5 Symmetrically branched crack in finite plate under tension
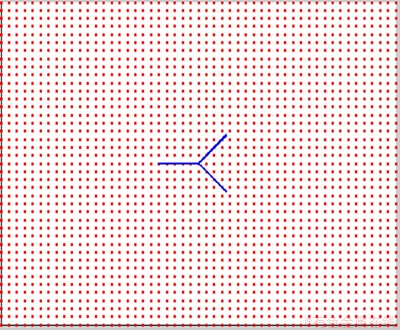
图6 有限平板分叉裂纹无网格模型图
Fig. 6 Meshless model for branched crack in finite plate under tension
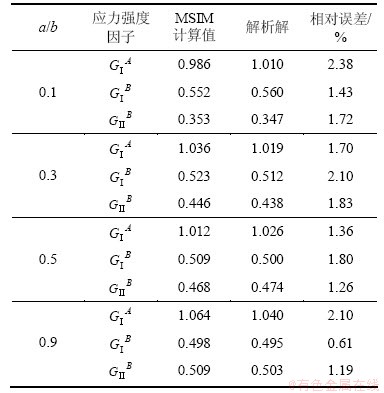
采用50×50的无网格结点进行计算。表1所示为用MSIM方法计算得到的结果与解析解的结果,可以发现本文结果与解析解吻合较好,最大相对误差仅为2.38%。
表1 分叉裂纹的应力强度因子
Table 1 Stress intensity factors for a branched crack
3.2 带水平裂纹的悬臂梁试件裂纹扩展模拟
图7所示为集中荷载作用下带水平边裂纹的悬臂梁试件。其中:W=6 m;H=1 m;水平边裂纹位于板中间H=1 m处;F表示一对作用于悬臂梁左端的集中力,悬臂梁右端为位移固定端。分析中共布置1 261个离散结点。图8所示为无网格计算模型图,图9所示为MSIM方法模拟裂纹扩展的路径。通过与Zhang等[32]用数值流形方法(NMM)所得的扩展路径相比较(图10),用无网格流形MSIM方法和用数值流形方法(NMM)所得的扩展路径吻合较好。
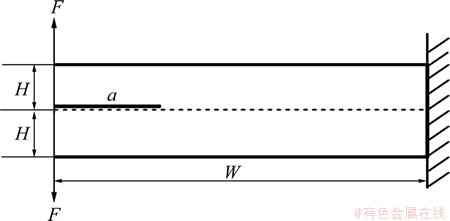
图7 集中力作用下的带水平裂纹的悬臂梁试件
Fig. 7 Cantilever beam with edge crack under concentrated forces

图8 悬臂梁裂纹无网格模型图
Fig. 8 Meshless model for cantilever beam with edge crack under concentrated forces
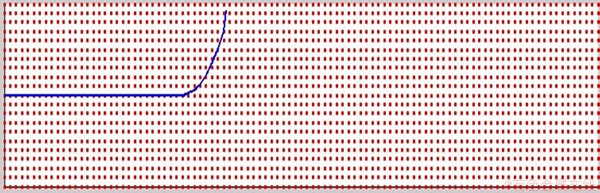
图9 裂纹扩展过程中的某一状态
Fig. 9 One stage of crack growth of cantilever beam with edge crack under concentrated forces

图10 NMM与MSIM裂纹扩展路径比较
Fig. 10 Comparison of crack growth path between MSIM and NMM
3.3 含5条竖向平行裂纹的三弯点梁裂纹扩展模拟
图11所示为1个含有5条竖向平行裂纹的三弯点梁试件,其中梁高H=0.2 m,梁的长度W=1 m。5条裂纹在梁长方向上等间距分布,5条初始裂纹的长度相等,均为0.02 m,在梁的上边缘中心点作用集中力为F。图12所示为无网格离散模型图,在分析中共布置了2 584个离散结点;图13所示为无网格流形MSIM方法模拟裂纹扩展状态图。通过与Elisa[33]用扩展有限元(XFEM)所得的扩展路径相比较(图14和图15),用无网格流形MSIM方法和用扩展有限元(XFEM)方法所得的扩展路径吻合较好。
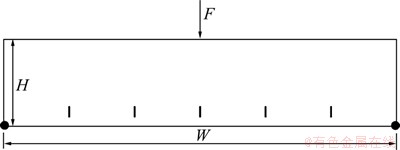
图11 含5条裂纹的三弯点梁试件
Fig. 11 Three point bending beam containing five parallel cracks

图12 含5条裂纹的三弯点梁无网格模型图
Fig. 12 Meshless model for three point bending beam containing five parallel cracks
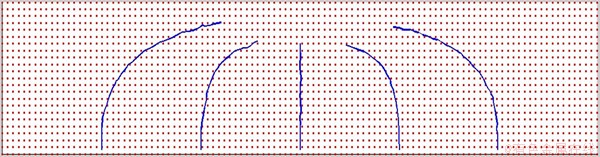
图13 含5条裂纹的三弯点梁裂纹扩展过程中的某一状态
Fig. 13 One stage of crack growth of three point bending beam containing five parallel cracks
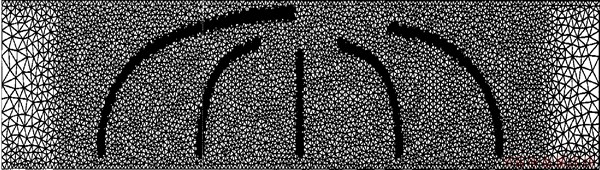
图14 含5条裂纹的三弯点梁 XFEM 裂纹扩展模拟图
Fig. 14 XFEM crack growth simulation for three point bending beam containing five parallel cracks
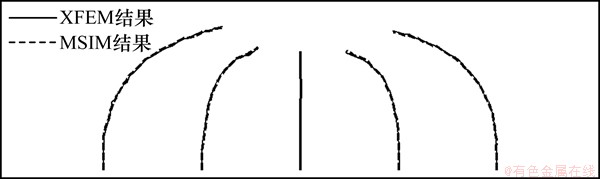
图15 含5条裂纹的三弯点梁MSIM和XFEM计算的扩展路径比较结果
Fig. 15 Comparison of crack growth path between MSIM and XFEM
4 结论
(1) 结合单位分解法和有限覆盖技术提出的无网格流形MSIM方法可以克服或减少目前无网格流形方法所面临的主要困难。该方法兼具无网格摆脱单元限制和流形方法易于处理不连续分析的优点,且可以在位移边界处的节点满足Kronecher-delta属性,克服了目前基于MLS插值的无网格流形方法本质条件难以施加,计算复杂、计算时间长等困难。
(2) 将MSIM方法推广应用于复杂应力状态下裂纹扩展过程的追踪模拟与分析,给出了相应的理论和具体的实现方法。数值算例表明所提出理论和方法的正确性和对解决非连续问题的可行性和有效性。
参考文献:
[1] Daux C, Moes N, Dolbow J, et al. Arbitrary branched and intersecting cracks with the extended finite element method[J]. International Journal for Numerical Methods in Engineering, 2000, 48(2): 1741-1760.
[2] 沈成康. 断裂力学[M]. 上海: 同济大学出版社, 1995: 70-96.
SHEN Chengkang. Fracture mechanics[M]. Shanghai: Tongji University Press, 1995: 70-96.
[3] 张行. 断裂力学[M]. 北京: 中国宇航出版社, 1990: 20-64.
ZHANG Xing. Fracture mechanics[M]. Beijing: Astronautics Publishing House, 1990: 20-64.
[4] 王水林, 冯夏庭, 葛修润. 高阶流形方法模拟裂纹扩展研究[J]. 岩土力学, 2003, 24(4): 621-625.
WANG Shuilin, FENG Xiating, GE Xiurui. Study on crack propagation modeling by high ordermanifold method[J]. Rock and Soil Mechanics, 2003, 24(4): 621-625.
[5] 唐辉明, 晏同珍. 岩石断裂力学理论与工程应用[M]. 武汉: 中国地质大学出版社, 1993: 122-134.
TANG Huiming, YAN Tongzhen. Fracture mechanics theory and its application of the rock[M]. Wuhan: China University of Geosciences Press, 1993: 122-134.
[6] 王水林. 数值流形方法与裂纹扩展的模拟[D]. 武汉: 中国科学院武汉岩土力学研究所, 1998: 24-30.
WANG Shuilin. Numerical manifold method and crack growth modeling[D]. Wuhan: Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, 1998: 24-30.
[7] Tradegard A, Nilsson F, Ostlund S. FEM-remeshing technique applied to crack growth problems[J]. Computer Methods in Applied Mechanics and Engineering, 1998, 160(10): 115-131.
[8] Bouchard P O, Bay F, Chastel Y. Numerical modeling of crack propagation:automatic remeshing and comparison of different criteria[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(16): 3887-3908.
[9] Benzley S E. Representation of singularities with isoperimetric finite elements[J]. International Journal for Numerical Methods in Engineering, 1974, 8(21): 537-545.
[10] Gingold R A, Moraghan J J. Smoothed particle hydrodynamics: Theory and applications to non-spherical stars[J]. Monthly Notice of the Royal Astronomical Society, 1977, 18(6): 375-389.
[11] Liu G R, Gu Y T. A point interpolation method for two- dimensional solids[J]. International Journal for Numerical Methods in Engineering, 2001, 50(12): 937-951.
[12] Atluri S N, Zhu T. A new Meshless local Petrov-Galerkin (MLPG) approach in computational mechanics[J]. Computational Mechanics, 1998, 22(2): 117-127.
[13] Belytschko T, Krongauz Y, Organ D. Meshless methods: An overview and recent developments[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139(2): 3-47.
[14] Belytschko T, Lu Y Y, Gu L. Element-free Galerkin method [J]. International Journal for Numerical Methods in Engineering, 1994, 37(8): 229-256.
[15] Gu Y T, Wang Q X, Lam K Y. A meshless local Kriging method for large deformation analyses[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(2): 1673-1684.
[16] Fernandez S, Huerta A. Imposing essential boundary conditions in mesh-free methods[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(6): 1257-1275.
[17] Belytschko T, Organ D, Krongauz Y. A Coupled finite element- element free Galerkin method[J]. Computational Mechanics, 1995, 17(6): 186-195.
[18] Shyu K, Salami M R. Manifold method with four-node isoperimetric finite element method[C]// Working Formn on the Manifold of Material Analysis. California, USA, 1995: 165-182.
[19] Shi G H. Manifold method[C]// Proceedings of the First Int Forum on Discon Defor Anal & Simu of Discon. Media, Berkeley, California. USA, 1996: 52-204
[20] Shi G H. Modeling rock joints and blocks by manifold method[C]// Proceedings of 32nd U.S. Symposium on Rock Mechanics. Santa Fe, New Mexico, 1992: 639-648.
[21] 蔡永昌, 朱合华, 夏才初. 流形方法覆盖系统自动生成算法研究[J]. 同济大学学报(自然科学版), 2004, 32(5): 585-590.
CAI Yongchang, ZHU Hehua, XIA Caichu. Automatically forming of cover system in numerical manifold method[J]. Journal of Tongji University (Natural Science), 2004, 32(5): 585-590.
[22] 李树忱, 程玉民, 李术才. 扩展的无网格流形方法[J]. 岩石力学与工程学报, 2005, 24(12): 2065-2073.
LI Shuchen, CHENG Yumin, LI Shucai. Enriched meshless manifold method[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(12): 2065-2073.
[23] 李树忱,程玉民. 基于单位分解法的无网格流形方法[J]. 力学学报, 2004, 36(4): 496-500.
LI Shuchen, CHENG Yumin. Meshless numerical manifold method based on unit partition[J]. Acta Mechanica Sinica, 2004, 36(4): 496-500.
[24] 田荣. 连续与非连续变形分析的有限覆盖无网格方法及其应用研究[D]. 大连: 大连理工大学水利工程学院, 2000: 112-134.
TIAN Rong. Finite-cover-based element-free method for continuous and discontinuous deformation analysis with applications in geotechnicalengineering[D]. Dalian: Dalian University of Technology. School of Hydraulic Engineering, 2000: 112-134.
[25] Cai Y C, Zhu H H. A PU-based meshless Shepard interpolation method satisfying delta property[J]. Engineering Analysis with Boundary Elements, 2009, 34(2): 9-16.
[26] Cai Y C, Zhu H H. A local meshless Shepard and least square interpolation method based on local weak form[J]. Computer Modeling in Engineering and Sciences (CMES), 2008, 34(2): 179-204.
[27] Lancaster P, Salkauskas K. Surfaces generated by moving least squares methods[J]. Mathematics of Computation, 1981, 37(2): 141-158.
[28] 刘桂荣, 顾元通. 无网格法理论及程序设计[M]. 济南: 山东大学出版社, 2007: 100-107.
LIU Guirong, GU Yuantong. An introduction to meshfree methods and their programming[M]. Jinan: Shandong University Press, 2007: 100-107.
[29] Rice J. A path independent integral and approximate analysis of strain concentration by notches and cracks[J]. Journal of App1ied Mechanics, 1968, 35(2): 379-386.
[30] 蔡永昌, 朱合华. 裂纹扩展过程模拟的无网格MSLS方法[J]. 工程力学, 2010, 27(7): 21-27.
CAI Yongchang, ZHU Hehua. Simulation of crack growth by the MSLS method[J]. Engineering Mechanics, 2010, 27(7): 21-27.
[31] Chen Y, Hasebe N. New integration scheme for the branch crack problem[J]. Engineering Fracture Mechanics, 1995, 52(2): 791-801.
[32] Zhang H H, Li L X, An X M, et al. Numerical analysis of 2-D crack propagation problems using the numerical manifold method[J]. Engineering Analysis with Boundary Elements, 2010, 34(2): 41-50.
[33] Elisa R L. Multiple crack growth by extended finite element method[D]. Evanston, USA: Northwestern University. School of Engineering and Applied Science, 2004: 145-147.
(编辑 杨幼平)
收稿日期:2013-07-28;修回日期:2013-10-25
基金项目:国家自然科学基金资助项目(10972161);国家重点基础研究发展计划(“973”计划)项目(2011CB013800)
通信作者:苏锋(1979-),男,甘肃兰州人,博士,从事岩石力学与地下工程等研究;电话:13616547548;E-mail: sufeng0205@163.com
摘要:采用一种新的无网格流形MSIM方法来进行裂纹扩展过程的模拟分析。该方法利用单位分解法和有限覆盖技术来构造插值函数,该插值函数的建立不受域内不连续面的影响,可较好地求解裂纹扩展问题;此外,该插值函数还具有高阶完备性、一致性,且可以在需要的节点处具备delta属性,能够方便、准确地施加各种边界条件。与通常的无网格方法相比,该方法由于采用了有限覆盖技术,试函数的构造不受域内不连续面的影响,克服了传统的无网格方法在处理不连续问题时由于采用光线法所遇到的困难;与数值流形方法相比,该方法用一系列节点的影响域来建立有限覆盖和单位分解函数,具有无网格方法的特性,摆脱了传统数值流形方法中在处理复杂非连续问题时网格所带来的困难,且其覆盖系统的生成远比数值流形方法中覆盖系统的生成简单。数值算例结果表明本文方法用于追踪复杂应力状态下裂纹扩展过程的正确性和有效性。
[2] 沈成康. 断裂力学[M]. 上海: 同济大学出版社, 1995: 70-96.
[3] 张行. 断裂力学[M]. 北京: 中国宇航出版社, 1990: 20-64.
[4] 王水林, 冯夏庭, 葛修润. 高阶流形方法模拟裂纹扩展研究[J]. 岩土力学, 2003, 24(4): 621-625.
[5] 唐辉明, 晏同珍. 岩石断裂力学理论与工程应用[M]. 武汉: 中国地质大学出版社, 1993: 122-134.
[6] 王水林. 数值流形方法与裂纹扩展的模拟[D]. 武汉: 中国科学院武汉岩土力学研究所, 1998: 24-30.
[21] 蔡永昌, 朱合华, 夏才初. 流形方法覆盖系统自动生成算法研究[J]. 同济大学学报(自然科学版), 2004, 32(5): 585-590.
[22] 李树忱, 程玉民, 李术才. 扩展的无网格流形方法[J]. 岩石力学与工程学报, 2005, 24(12): 2065-2073.
[23] 李树忱,程玉民. 基于单位分解法的无网格流形方法[J]. 力学学报, 2004, 36(4): 496-500.
[24] 田荣. 连续与非连续变形分析的有限覆盖无网格方法及其应用研究[D]. 大连: 大连理工大学水利工程学院, 2000: 112-134.
[28] 刘桂荣, 顾元通. 无网格法理论及程序设计[M]. 济南: 山东大学出版社, 2007: 100-107.
[30] 蔡永昌, 朱合华. 裂纹扩展过程模拟的无网格MSLS方法[J]. 工程力学, 2010, 27(7): 21-27.


