Article ID: 1003-6326(2005)05-1085-04
Maximum solid solubility of transition metals in vanadium solvent
ZHANG Jin-long(张金龙)1, FANG Shou-shi(方守狮)1, ZHOU Zi-qiang(周自强)1,
LIN Gen-wen(林根文)1, GE Jian-sheng(葛建生)1, FENG Feng(冯 锋)2
(1. Institute of Hydrogen Storage Materials, Shanghai University, Shanghai 200072, China;
2. Department of Mechanical, Automotive and Materials Engineering, University of Windsor, Windsor, Ont., Canada N9B 3P4)
Abstract:
Maximum solid solubility (Cmax) of different transition metals in metal solvent can be described by a semi-empirical equation using function Zf that contains electronegativity difference, atomic diameter and electron concentration. The relation between Cmax and these parameters of transition metals in vanadium solvent was studied. It is shown that the relation of Cmax and function Zf can be expressed as lnCmax=Zf=7.3165-2.7805(ΔX)2-71.278δ2-0.85556n2/3. The factor of atomic size parameter has the largest effect on the Cmax of the V binary alloy; followed by the factor of electronegativity difference; the electrons concentration has the smallest effect among the three bond parameters. Function Zf is used for predicting the unknown Cmax of the transition metals in vanadium solvent. The results are compared with Darken-Gurry theorem, which can be deduced by the obtained function Zf in this work.
Key words:
solid solubility; vanadium alloys; function Zf; electronegativity difference; atomic size parameters; electron concentration CLC number: TG139.7;
Document code: A
1 INTRODUCTION
Recently, alloys with a high density of hydrogen were enthusiastically studied not only for high-performance negative electrodes, but also for fuel cells or for other applications. Vanadium or V-based solid solution alloys with BCC structure are very attractive because of their high hydrogen absorption and desorption capacity at moderate pressure and temperature[1, 2]. Another reason is that the diffusion rate of hydrogen in vanadium is extremely high. The hydrogenation properties of vanadium have been controlled and improved by alloying with other metals[3-6].
The maximum solid solubility Cmax of alloys is one of the basic issues of the theoretical research on phase formation. It is significant to understand the phase formation theory and improve the ability to predict extensive solid solutions, which restricts the possible adjustment range of components in vanadium alloys. It is also important for V-based solid solution alloys to apply for fuel cells and Ni-MH batteries. There are some theories to analyze the solid solubility such as Hume-Rotherys Rules, Paulings Electronegativity Concept and Friedels electronic theory, which respectively emphasize the effects of the electronegativity, atomic size and outer layer electron[7]. Darken and Gurry[8] proposed a method by considering both atomic diameter and electronegativity to predict the formation of solid solution alloys. However, there are some questions that can not be explained. Function Zf has been successfully proposed to calculate the Cmax of transition metals in Ti, Zr, Hf and Pd solvents in our previous work, which is convenient to know the relative contributions of atomic parameters[9-14]. In this paper, we shall deal with Cmax of transition metals in vanadium by function Zf and determine which is the main atomic factor effect on Cmax.
2 MATHEMATICAL MODEL FOR RELATION BETWEEN Cmax AND FUNCTION Zf
2.1 Mathematical model
According to our previous work[9-14], there is a relation between the Cmax of transition metals dissolved in a given solvent metal and the function Zf.
lnCmax=Zf(1)
and the function Zf is defined as
Zf=a0+a1(ΔX)2+a2δ2+a3n2/3(2)
where ΔX=X0-X, is the electronegativity difference between solute and solvent element (subscript 0 means solvent, it has the same meaning in D0 and n0 below); δ=1-D/D0 is the atomic size difference between solute and solvent element; n=(n0+n1)/2 is the average out-layer electrons of solute and solvent element; a1, a2 and a3 are the proportional coefficients and a0 is a constant, which needs to be fixed.
2.2 Determining of coefficients in function Zf of vanadium binary alloys
The coefficients in function Zf of the binary alloys for a given solvent can be fixed using a regression analysis from the known data of Cmax, X ,δ and n. The Cmax data of the binary alloys for a given solvent can be read from the equilibrium phase diagrams[15] and the other data were read as that in Ref.[16].
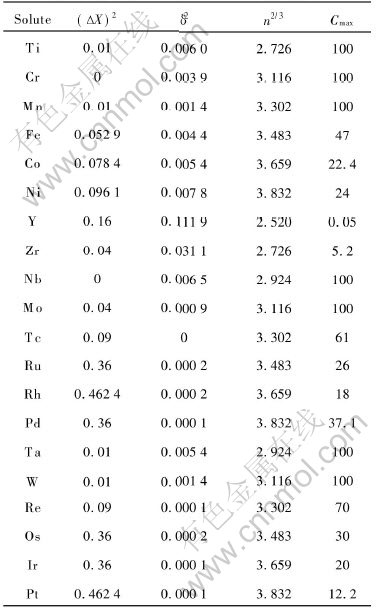
For the vanadium binary alloys the data needed to determine the coefficients in function Zf are listed in Table 1.
Table 1 Data of Cmax, electronegativity difference ΔX, atomic size parameter δ and
electron concentration n for solvent V
3 RESULTS AND DISCUSSION
3.1 Function Zf of vanadium binary alloys
Function Zf of vanadium binary alloys is obtained by a regression analysis using the proposed model.
Zf=lnCmax=7.3165-2.7805(ΔX)2-
71.278δ2-0.85556n2/3(3)
[BJ(,,,][BJ)] Vol.15 №.5 Maximum solid solubility of transition metals in vanadium solvent The correlation coefficient of Eqn.(3) is 0.98. Fig.1 shows a comparison between the calculated and experimental values of lnCmax for V alloys. It can be seen from Fig.1 that the values of lnCmax calculated from Eqn.(3) are in good agreement with the experimental data.
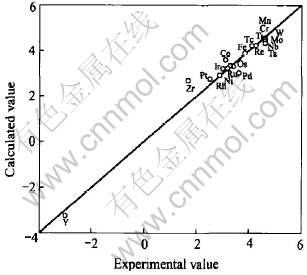
Fig.1 Comparison between calculated and experimental values of lnCmax
3.2 Application of function Zf
Function Zf can be easily used for dealing with the following questions of the Cmax of transition metals in a given solvent.
Cmax and function Zf can be expressed as an equation of the three factors: electronegativity difference(ΔX), atomic size parameter δ and electron concentration n on the basis of energetics of alloys. According to the theory of regression analysis, it can determine the relative contribution by comparing the statistic values Fi.
Table 2 lists the statistic Fi of items in the Eqn.(3) by regression analysis. It is well known according to the theory of regression analysis that the larger the statistic values of the Fi items, the larger the effect of the item is. Therefore, it can be deduced from Table 2 that the factor of atomic size parameter (δ2) has the largest effect on the Cmax of the V binary alloy, followed by the factor of electronegativity difference; the electrons concentration (n2/3) has the smallest effect among the three bond parameters, yet it cannot be neglected.
The values of the unknown Cmax of some transition metals solved in vanadium can be predicted by Eqn.(3). Table 3 lists the prediction values and the fiducial range of Cmax of some transition metals solved in vanadium whose maximum solid solution limits are not sure from the phase diagram.
Function Zf can explain the rules of D-G theo rem, which is proved to be the special examples of Cmax equation by neglecting some certain items[12]. According to the Cmax equation, when Cmax is set to Cmax0, it is easy to get a Z-F ellipse equation:
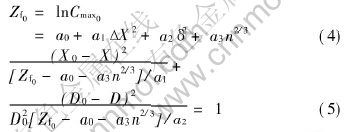
Table 2 Values of statistic items in Eqn.(3)
Table 3 Prediction values of Cmax and their atomic parameters

Eqn.(5) is an ellipse when Zf0-a0-a3n2/3=k, that the central coordinate is point (X0, D0) and the long and short axis are ![]() and
and![]() respectively. We can obtain the D-G theorem just by letting
respectively. We can obtain the D-G theorem just by letting ![]() =X±0.4 for abscissa and
=X±0.4 for abscissa and ![]() =D0±15% for vertical coordinate, which is the conditions for D-G theorem coming into existence.
=D0±15% for vertical coordinate, which is the conditions for D-G theorem coming into existence.
Thus, D-G ellipse of V binary alloys can be expressed as
![]()
The shape and size of the ellipse drawn by Eqn.(5) are influenced by the value of Zf0-a0-a3n2/3. The effects of n on the shape and size of Z-F ellipse equation of V binary alloys when Cmax0=50% are expressed as Eqn.(7).

D-G theorem can be seen as a special example of Z-F ellipse equation in which omitting the effect of item n2/3 is omitted by comparing Eqn.(6) with Eqn.(7).
D-G ellipse that the minor axis is Dv±15% (abscissa) and the major axis is X±0.4 (ordinate) is shown in Fig.2. The center of the ellipse is at (2.72, 1.6) that stands for the atomic diameter and electronegativity of vanadium respectively. Cmax of most transition metals (Ta, W, Nb, Mo, Ti, Cr, Mn, Fe, Re, Tc) in vanadium in the ellipsoid are larger than 50%, which is in agreement with the D-G method. But Cmax of other transition metals (Co, Ni) are less than 50%, which is not in agreement with D-G method. Cmax out of the ellipsoid (La, Y, Sc, Hf, Zr, Os, Ru, Ir, Rh, Pt, Pd) are less than 50%, which is in agreement with D-G method. Thus the rules of variable Cmax of most transition metals (not all solute) in vanadium can be judged according to D-G method. It mainly ascribes to the reason that all the d-group elements have the common metallic structures and have d-electrons, when one substitutes a d-group solute element into the d-group solvent there is no major distortion of the electronic bands and no large change in the total energy of the system[7, 8].

Fig.2 D-G ellipse and Z-F ellipse about solvent vanadium
Z-F ellipse equation of V binary alloys when n=6.4 is expressed as Eqn.(8) and shown in Fig.2. It is clear that Cmax of (Co, Ni) are in D-G ellipse, but outside Z-F ellipse. Function Zf theory is in agreement with the experiment that Cmax of all elements in Z-F ellipse are larger than 50% while it is smaller than 50% for the element outside the ellipse.
Function Zf can also be applied to explain M-C theorem that Miedema -Chelikowsky estimated the value of solid solubility by a dimensional chart with parameters n1/3 and Φ* which is relative with electronegativity. Function Zf can also be applied to explain the rule of electron concentration[12].
4 CONCLUSIONS
1) The maximum solid solubility of transition metals in vanadium can be represented as function Zf of electronegativity difference, atomic size parameter and electron concentration as follows: lnCmax=Zf=a0+a1(ΔX)2+a2δ2+a3n2/3.
2) The factor of atomic size parameter has the largest effect on the Cmax of the V binary alloy, followed by the factor of electronegativity difference; the electrons concentration has the smallest effect among the three bond parameters.
3) Function Zf can be applied to determine the main atomic factor effect on Cmax and predict Cmax of transition metals in vanadium solvent. Function Zf can also be applied to explain D-G theorem.
REFERENCES
[1]Kim J H, Lee H, Lee P S, et al. A study on the improvement of the cyclic durability by Cr substitution in V-Ti alloy and surface modification by the ball-milling process [J]. J Alloys & Compounds, 2003, 348: 293-300.
[2]Uno M, Takahashi K, Maruyama T, et al. Hydrogen solubility of BCC titanium alloys [J]. J Alloys & Compounds, 2004, 366: 213-216.
[3]ZHU Y F, PAN H G, GAO M X, et al. Influence of annealing treatment on Laves phase compound containing a V-based BCC solid solution phase—Part I: Crystal structures [J]. International Journal of Hydrogen Energy, 2003, 28: 389-394.
[4]LI R, PAN H G, GAO M X, et al. Structural and electrochemical properties of hydrogen storage alloys Ti0.8Zr0.2V2.7Mn0.5Cr0.8Nix (x=1.50-2.25) [J]. J Alloys & Compounds, 2004, 373: 223-230.
[5]Avashima H, Takahashi F, Ebisawa T, et al. Correlation between hydrogen storage properties and homogeneity of TiVCr alloys [J]. J of Alloys & Compounds, 2003, 356-357: 405-428.
[6]CHAI Yu-jun, ZHAO Min-shou. Structure and electrochemical properties of Ti0.25V0.35Cr0.40-xNix (x=0.05-0.40) [J]. International Journal of Hydrogen Energy, 2005, 30: 279-283.
[7]Gschneidner K A, Larry L S. Darkens contributions to the theory of alloy formation and where we are today [A]. Bennett L H. Theory of Alloy Phase Formation [C]. A Publication of the Metallurgical Society of AIME, 1980. 1-39.
[8]Darken L S, Gurry R W. Physical Chemistry of Metals [M]. New York: McGraw-Hill Co Inc, 1953. 74-92.
[9]ZHOU Zi-qing, FANG Shou-shi, FENG Feng. Rules for the maximum solid solubility of transition metals in Ti, Zr and Hf solvents [J]. Trans Nonferrous Met Soc China, 2003, 13(4): 864-868.
[10]FANG Shou-shi, LIN Gen-wen, ZHANG Jin-long, et al. The maximum solid solubility of the transition metals in palladium [J]. International Journal of Hydrogen Energy, 2002, 27: 329-332.
[11]ZHOU Zi-qing, ZHANG Jin-long, PING Xin-yi, et al. The maximum solid solubility of the transition metals in titanium alloys [A]. Advance in Energy Sources Materials, Intelligent Materials and Gradient Materials [C]. Beijing: Metallurgical Industry Press, 1998. 37-40. (in Chinese)
[12]ZHOU Zi-qing, FANG Shou-shi, FENG Feng. Comparison between methods for predicting maximum solid solubility of transition metals in solvent metal [J]. Trans Nonferrous Met Soc China, 2003, 13(5): 1185-1189.
[13]ZHOU Zi-qing, ZHANG Jin-long, GE Jian-sheng, et al. Effect of 3d transition-metal additive on the hydrogen storage properties of Mm1-xMlxNi5-yMy alloys [A]. Ohta T, Homma T. New Energy Systems and Conversions [C]. Universal Academy Press, 1993. 79.
[14]FANG Shou-shi, ZHOU Zi-qing, ZHANG Jin-long, et al. Two mathematical models for the hydrogen storage properties of AB2 type alloys [J]. J Alloys & Compounds, 1999, 293-295: 10-13.
[15]Massalski T B. Binary Alloy Phase Diagrams [M]. Ohio: ASM, Metals Park, 1996.
[16]XIAO Ji-mei. Energetics of Alloys [M]. Shanghai: Shanghai Science and Technology Press, 1985. 296.(in Chinese)
Foundation item: Project(045211019) supported by Shanghai Municipal Commission of Science and Technology
Received date: 2004-12-22; Accepted date: 2005-05-09
Correspondence: ZHOU Zi-qiang, Professor; Tel: +86-21-56651556; E-mail: zqzhou408@21cn.com


