
J. Cent. South Univ. (2021) 28: 898-910
DOI: https://doi.org/10.1007/s11771-021-4652-7
Prediction of resilient modulus for subgrade soils based on ANN approach
ZHANG Jun-hui(张军辉)1, HU Jian-kun(胡健坤)1, PENG Jun-hui(彭俊辉)1,FAN Hai-shan(范海山)1, ZHOU Chao(周超)2
1. National Engineering Laboratory of Highway Maintenance Technology, Changsha University of Science & Technology, Changsha 410114, China;
2. Department of Civil and Environmental Engineering, The Hong Kong Polytechnic University,Hong Kong 999077, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Abstract:
The resilient modulus (MR) of subgrade soils is usually used to characterize the stiffness of subgrade and is a crucial parameter in pavement design. In order to determine the resilient modulus of compacted subgrade soils quickly and accurately, an optimized artificial neural network (ANN) approach based on the multi-population genetic algorithm (MPGA) was proposed in this study. The MPGA overcomes the problems of the traditional ANN such as low efficiency, local optimum and over-fitting. The developed optimized ANN method consists of ten input variables, twenty-one hidden neurons, and one output variable. The physical properties (liquid limit, plastic limit, plasticity index, 0.075 mm passing percentage, maximum dry density, optimum moisture content), state variables (degree of compaction, moisture content) and stress variables (confining pressure, deviatoric stress) of subgrade soils were selected as input variables. The MR was directly used as the output variable. Then, adopting a large amount of experimental data from existing literature, the developed optimized ANN method was compared with the existing representative estimation methods. The results show that the developed optimized ANN method has the advantages of fast speed, strong generalization ability and good accuracy in MR estimation.
Key words:
Cite this article as:
ZHANG Jun-hui, HU Jian-kun, PENG Jun-hui, FAN Hai-shan, ZHOU Chao. Prediction of resilient modulus for subgrade soils based on ANN approach [J]. Journal of Central South University, 2021, 28(3): 898-910.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-021-4652-71 Introduction
The resilient modulus (MR) of subgrade soils, as the characterization parameter of stiffness, describes the non-linear stress-strain characteristics of subgrade soils and reflects the dynamic characteristics under vehicular traffic loading [1, 2]. Because of the major impact on the pavement performance, the resilient modulus has been widely used in mechanistic pavement thickness design [3], such as AASHTO [4] and the Mechanistic Empirical Pavement Design Guide (MEPDG) [5]. Therefore, accurately predicting the resilient modulus of subgrade soils is essential to build a durable pavement.
At present, the resilient modulus prediction methods can be classified into three categories [6]. The method in Category I is a back-calculation based on non-destructive testing technology, such as falling weight deflectometer (FWD). The method in Category II is a laboratory repeated load triaxial test, and the method in Category III is to adopt the prediction models. The method in Category I can be used to the existing subgrades, and the method in Category II is time-consuming and cumbersome. Compared to methods in Category I and Category II, establishing prediction models of subgrade soils is much simpler and more efficient. Therefore, many related researches have been carried out.
Firstly, SEED et al [7] introduced the resilient modulus when studying the relationship between the resilient characteristic of subgrade soils and the fatigue failure of asphalt concrete pavement, and defined it as the ratio of the deviator stress to the recoverable resilient strain. And then, many researchers developed a great many models to predict MR of subgrade soils, such as SEED et al [8], UZAN et al [9, 10]. Among them, the widely accepted one is the model presented by National Cooperative Highway Research Program 1-28A [11], as shown in Eq. (1):
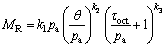 (1)
(1)
where τoct is the octahedral shear stress, 
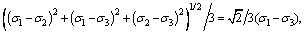 kPa; θ is the bulk stress, θ=σ1+σ2+σ3, kPa; σ1, σ2, σ3 are the maximum principal stress, the intermediate principal stress and the minor principal stress, respectively; pa is the atmospheric pressure, pa=101.3 kPa; k1, k2 and k3 are the regression coefficients.
kPa; θ is the bulk stress, θ=σ1+σ2+σ3, kPa; σ1, σ2, σ3 are the maximum principal stress, the intermediate principal stress and the minor principal stress, respectively; pa is the atmospheric pressure, pa=101.3 kPa; k1, k2 and k3 are the regression coefficients.
Since then, by incorporating the matric suction, many researchers have established moisture-dependent MR models based on Eq. (1) [12-15]. Although using these models to predict the resilient modulus has higher accuracy, different model coefficients are required for different soil samples. To solve this problem, many researchers found that there was a strong correlation between physical properties of soils and model coefficients.
YAO et al [16] analyzed the influence of matric suction and stress state on resilient modulus and proposed the predictive equation of resilient modulus with the minimum bulk stress, octahedral shear stress, and matric suction, as shown in Eq. (2):
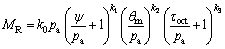 (2)
(2)
where θm is the minimum bulk stress, θm=θ-σd, kPa; ψ is the matric suction, kPa; k0-k3 are the model coefficients.
Combined with the experimental data from exciting literature and the established MR prediction model, the correlation between physical properties of soils and model coefficients was proposed as following:
 (3)
(3)
where Ip is the the plasticity index; ωl is the liquid limit, P0.075 is 0.075 mm passing percentage; and dry density γd is the physical properties of the subgrade soils.
ZHANG et al [15] conducted multiple regression analyses on 22 soil samples and established a more widely used relationship based on Eq. (2), which presented the relationship between physical properties of soils and model coefficients of subgrade soils, as shown in Eq. (4):
 (4)
(4)
where liquid limit ωl, plasticity index IP, maximum dry density γdmax, saturated volume moisture content θs, 0.075 mm passing percentage P0.075, dry density γd, optimum moisture content ωopt are physical properties of subgrade soils; DmaxP is the product of 0.075 mm passing percentage P0.075 and the maximum dry density γdmax, as shown in Eq. (5); DmaxIP is the product of the maximum dry density γdmax and the plasticity index IP, as shown in Eq. (6):
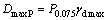 (5)
(5)
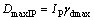 (6)
(6)
Although most of these models can predict the resilient modulus of different soil samples, some problems, like low precision and high prediction bias, still remain [17]. With the popularization of artificial intelligence, some researchers tried to use the artificial neural network prediction method to predict the resilient modulus [17-22]. The regression coefficients k1, k2 and k3 of one MR model were estimated through three different ANN models established by NAZZAL et al [19]. A three-layered artificial neural network model was established to predict the resilient modulus of nine different soil samples by KIM et al [18]. An adaptive neuro-fuzzy inference system was adopted to predict resilient modulus of flexible pavements subgrade soils and the sensitivity of selected input parameters is also analysed by SADROSSADAT et al [22]. To obtain the model coefficients of resilient modulus for plastic and non-plastic soils, two three-layered ANN models were performed by SAHA et al [17]. SADROSSADAT et al [21] established a new empirical equation through the experimental database and estimated resilient modulus by using gene expression programming approach. However, these ANN models are under-developed and have many defects now. Firstly, too few input variables selected will cause low prediction accuracy when the data volume is too large [18, 19]. Besides, for the method of establishing the relationship between physical properties of soils and model coefficients, different MR prediction models need to establish different equations, which will cause poor applicability [19]. Thirdly, using indirect estimation of the k coefficient to obtain the resilient modulus instead of directly estimating will lead to a quadratic error [17-19, 23].
In this study, adopting the experimental data from the existing literature, a dataset was established. Next, based on the dataset, an ANN method for the prediction of MR considering physical properties of soils, state variables and stress variables of subgrade soils was established. The physical properties of soils contain liquid limit (ωl), plastic limit (ωp), plasticity index (IP), 0.075mm passing percentage (P0.075), maximum dry density (γdmax), optimum moisture content (ωopt). The state variables include degree of compaction (K) and moisture content (ω). The confining pressure (θ) and deviatoric stress (σ) were contained in stress variables. And, the resilient modulus is directly used as the output layer. And then, the ANN approach was optimized by multi-population genetic algorithm. Finally, the generalization ability and accuracy of the developed optimized ANN method were evaluated by comparing to the existing representative estimation methods.
2 Establishment of optimized ANN prediction method
2.1 Basic principle
The artificial neural network originated from the MP model proposed by MCCULLOCH et al [24]. Because of its strong parallel distributed processing, nonlinear mapping, self-adaptive and self-organizing learning ability, artificial neural networks have been applied in many fields, such as information, medicine, and transportation, etc. NIELSEN [25] demonstrated with a visualization that artificial neural networks can approximate arbitrary nonlinear functions, which makes it more suitable for solving problems that are difficult for traditional numerical analysis methods. The network model can be divided into feedforward network and feedback network. In this study, the back-propagation (BP) neural network proposed by RUMELHART et al [26] in the prediction method is a typical feedforward network. The BP algorithm searches the loss by forwarding propagation and searches the error by back-propagation to update the network weight so that the output error can reach an expected one. The neural structure of the network is presented in Figure 1. Firstly, the input signal is normalized to make the network more convergent, and then the signal is linearly transformed into the hidden layer according to the forward propagation mode. At last, through the non-linearly transformed by the activation function, the signal reaches the output layer to obtain the output value. If the error between the output value and the true value is less than or equal to the expected, the output is what we need. Otherwise, the error signal will arrive at the input layer through the hidden layer in a back-propagation manner, and the network weight and threshold will be updated simultaneously. After updating all the weight and threshold, the network signal will get a new output according to the forward propagation mode until the error value is less than or equal to the expected.
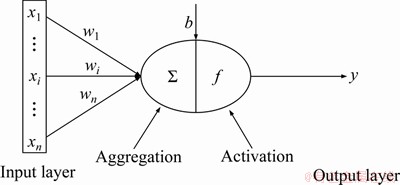
Figure 1 Diagram of neuron structure
The relationship between input and output variables of the neuron is illustrated in Eq. (7):
 (7)
(7)
where f is the activation function, generally using the sigmoid, tanh or relu function; yi is the output value; wji is the network weight; xi is the normalized input variable; bj is the bias, b≡-threshold.
The gradient descent algorithm was adopted to update the network weights, as given in the following equation:
 (8)
(8)
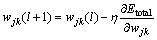 (9)
(9)
where ωij(l) and ωij(l+1) are the connection weights of training iteration l and l+1 between the i-th neuron in the input layer and the j-th neuron in the hidden layer, respectively; ωjk(l) and ωjk(l+1) are the connection weights of training iteration l and l+1 between the i-th neuron in the hidden layer and the j-th neuron in the output layer, respectively; η is the learning rate, η=0.1.
As presented in Eq. (10), Etotal was defined as the sum of squared errors, also known as the loss function:
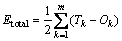 (10)
(10)
where m is the figure for output layer nodes; Tk is the target output; Ok is the value of the k output layer.
The gradient descent algorithm was used to update the network thresholds, as shown in Eq. (11):
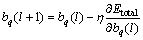 (11)
(11)
where bq(l) and bq(l+1) are the q-th biases at iteration l and l+1, respectively.
2.2 Prediction method of resilient modulus based on optimized ANN approach
The Matlab software was adopted in this study to write programs of artificial neural network. The activation function of the neural network is S (sigmoid) function, as shown in Eq. (12). The Levenberg-Marquardt optimization algorithm was selected as the training function to minimize the mean square error (MSE). Then the sum of squared errors was taken as the loss function, and the minimum value of the loss function was calculated by the gradient descent algorithm. As given in Figure 2, a three-layered network structure was applied in this study, which consists of the input layer, one single hidden layer, and the output layer. For the selection of input variables, too few input variables will lead to a large prediction error when there is too much data, and there will be too many tests and low efficiency when the input variables are too many. Some researchers have found that, for the same soil, the resilient modulus is significantly correlated with the state and stress variables [27-29]. At the same time, ZHANG et al [14] also found that, for different soils, the influence of state and stress variables on the resilient modulus will be affected by the physical properties of soils. Therefore, three categories of variables including physical properties of soils, state variables, and stress variables were selected as input variables in this study. Among them, the state variables include degree of compaction and moisture content, and the stress variables include confining pressure and deviatoric stress. It has been found that all of these variables are closely related to the resilient modulus [30]. Meanwhile, physical properties of soils such as liquid limit, plastic limit,plasticity index, 0.075 mm passing percentage, maximum dry density, and optimum moisture content were selected to ensure that the developed estimation method can be used to predict different soils, which have also been proved to have an impact on the value of resilient modulus [31, 32]. Subsequently, the number of input layer nodes (n1) is set to 10, including physical properties of soils, state variables and stress variables of subgrade soils. A relationship between the figure for hidden layer nodes (n2) and input layer nodes (n1) in this ANN method was established by SHI et al [33], as given in Eq. (13). Therefore, the number of the hidden layer nodes is 21. There is only one node in the output layer, which is the resilient modulus value. For this network structure, the mapping relationship between the input layer and output layer in the network can be shown in Eq. (14).
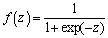 (12)
(12)
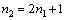 (13)
(13)
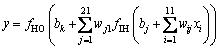 (14)
(14)
where fHO is the activation function between the hidden layer and the output layer; fIH is the activation function between the input layer and hidden layer; wij is the weight connection between the input layer and hidden layer; wj1 is the weight connection between the hidden layer and output layer; xi is the input variables; bj is the bias of the hidden layer; bk is the bias of the output layer [34, 35].
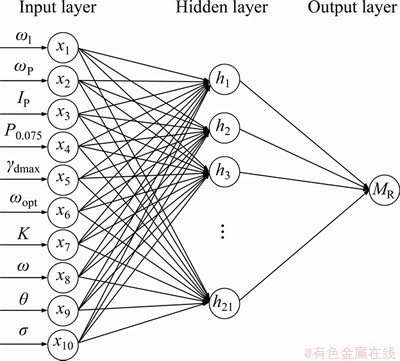
Figure 2 Typical three-layered neural network architecture
BP algorithm is an iterative learning algorithm based on gradient descent, which determined that it has many defects such as low convergence rate, getting into local minimum and possible oscillation when approaching the optimal solution, etc. Genetic algorithm (GA) is a method to find the optimal solution by simulating the natural evolution process [20]. Many researchers have used GA to optimize the initial weights and thresholds of BP neural network, to solve the shortcomings of BP algorithm [36-38]. However, BP neural network optimized by GA (GA-BP) requires a random interval to generate weights and thresholds. It is difficult to find the global optimal solution when the optimal weights and thresholds of the network are not in this interval. Besides, the offspring population has the same number of individuals as the parent population will lead to a low probability to produce elite individuals, which may also slow down the convergence rate of the network and make it easy to fall into the local optimum. To overcome these defects, the multi-population genetic algorithm was developed to optimize the network to search the optimal weights and thresholds, further to obtain the global optimal solution. In the first place, the parameters were initialized to determine the initial interval of weights and thresholds and the excepted error. Afterward, the initial population was generated within the interval to form the parent population. The fitness of individuals in the population was calculated based on the linear fitness function, and individuals with higher fitness were retained as elite individuals. Then, after intra-population selection, crossover, mutation, and competition, a new population was formed. Finally, the program calculated whether the output error of the network is less than or equal to the expected. If so, the calculation will be terminated and the network weights and thresholds will be output. Otherwise, the interval will be moved to form a new one and the program will be re-executed. The optimization flow chart of the neural network is presented in Figure 3.
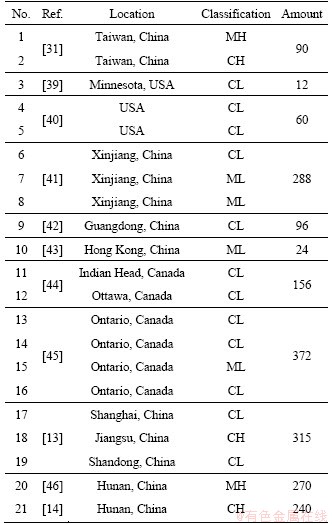
The sources of collected data of soil samples and the list of the soil parameters selected in this study are presented in Tables 1 and 2, respectively. A total of 1923 experimental data from existing literature were selected to establish the ANN approach. The data of these soil samples were collected from parts of China, the United States and Canada, which can be classified as low liquid limit clay (CL), low liquid limit silt (ML), high liquid limit clay (CH), and high liquid limit silt (MH). The range of ωl, ωp, IP, P0.075, γdmax, ωopt, K, ω, θ and σ are 19.6%-70.8%, 13.0%-35.2%, 6.0%-35.6%, 9.6%- 99.3%, 1.56-2.03 g/cm3, 11.5%-23.5%, 0.87-1.00, 8.1%-30.6%, 10-60 kPa and 10-105 kPa, respectively. The measured values of MR range from 7.98 to 362.14 MPa. It can be seen that the data of selected soil samples cover a wide range and are of certain representativeness. In these soil samples, 50% of them were used as the training set for building neural networks initially; 25% of them were used as the validation set for further optimization of weights and thresholds and making a preliminary evaluation of the model; the rest were used as the testing set to verify the accuracy of the established prediction method.
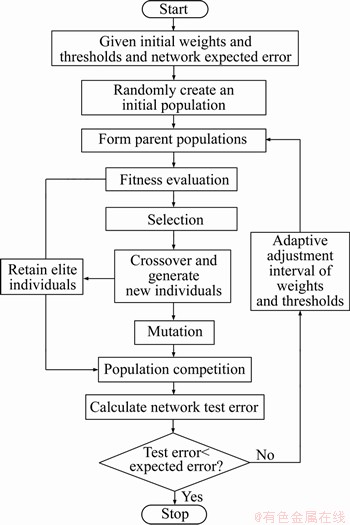
Figure 3 Flow chart of artificial neural network based on multi-population genetic algorithms
In this study, the coefficient of determination (R2) and the root mean square error (RMSE) were selected to assess the performance of the ANN method. R2 describes the fitting degree of the established method, which can be defined as the proportion of the variance in the dependent variable that is predictable from the independent variable (s). When R2≥0.9, it can be considered that the model has a perfect fit; a good fit can be defined when 0.70≤R2≤0.89; and it can be defined as a fair fit when R2 is in the range of 0.40-0.69 [30]. The comparison of the measured and predicted MR values by the ANN method has been presented in Figure 4. It can be seen from Figure 4 that the established estimation method has relatively high accuracy and can be applied to estimate the resilient modulus. Different data sets provided in Table 1 were considered to evaluate the accuracy of the model as shown in Figure 5. There are four types of soil were contained in these data sets. The high R2 and low RMSE indicate that the ANN method has a perfect fit. Because of fewer soil samples of MH and CH in Table 1 to train and validate, it can be seen that RMSE of No. 1 (MH) and No. 2 (CH) are higher than No. 6 (CL) and No. 7 (ML). This reflects the characteristics of ANN as a prediction method that needs a lot of training data to obtain higher accuracy.
Table 1 Source and classification of soil samples
2.3 Sensitivity analysis of independent variables
It is difficult to get the relative importance of each variable in the neural network using traditional sensitivity analysis methods. Many researchers have found that the importance of input variables to output variables can be obtained from the functional relationship of output variables to input variables and the connection weight between layer neurons [47-49]. In this study, GARSON algorithm was adopted to analyze the sensitivity of the ANN approach. The method uses the product of the absolute value of connection weights to calculate the relative importance of each input variable.As a representative of the sensitivity analysis method based on connection weight, it has been implemented by several researchers [34, 50].
Table 2 Soil parameters in soil sample database
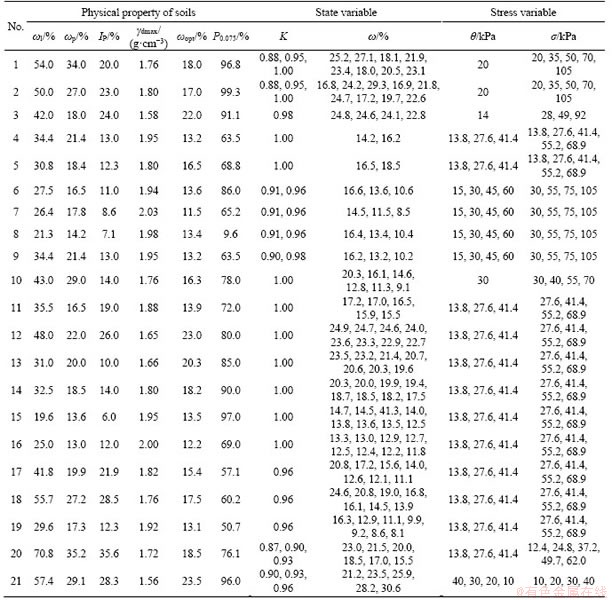
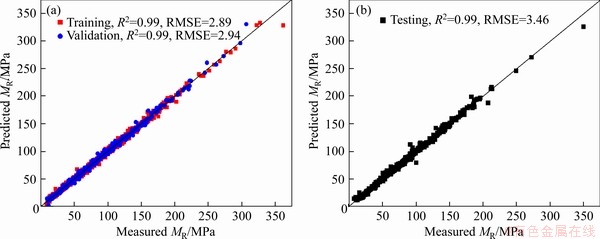
Figure 4 Measured versus predicted resilient modulus for training and validation data (a) and testing data (b)

Figure 5 Measured versus predicted resilient modulus on different data sets
Figure 6 shows the relative importance of each input variable. It is clear that the most significant variable is ωl, followed by P0.075, ωp, Ip, ωopt, γdmax, ω, K, θ, σ, respectively. And the relative importance of physical properties (ωl, ωp, Ip, P0.075, γdmax, ωopt), state variables (K, ω) and stress variables (θ, σ) are 85.77%, 13.53% and 0.70%, respectively. The physical properties represent the essential characteristics of soils, and the state variables describe the physical state of soils. Therefore, they account for a larger proportion. However, it should be noted that each input variable has a great contribution to MR. The sensitivity analysis just shows the comparison between input variables. Thus, none of them can be removed from these variables, even though the percentages of relative importance are at a low figure [20, 22, 34].
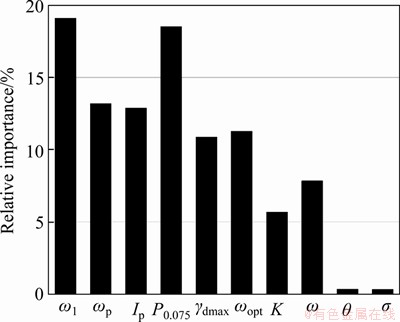
Figure 6 Relative importance of each input variables for ANN prediction method based on Garson algorithm
3 Comparative analysis of prediction methods
There are two methods to estimate the resilient modulus by prediction models. One way is to adopt the prediction model that requires many MR tests, as shown in the method of Eq. (1) presented by NCHRP [11]. The other way is to establish the relationship between physical properties of soils and the regression coefficients of MR models established by ZHANG et al [15]. It only requires testing the physical properties of soils. What these two methods have one thing in common is that they both predict the k coefficient first and then calculate the resilient modulus based on the prediction model. In this study, the prediction methods of NCHRP [11], ZHANG et al [15] and traditional ANN approach were selected and compared to detect the accuracy and applicability of the ANN approach based on MPGA. Combined with the experimental data in this study, five kinds of soil samples in Table 1 were randomly selected. And the k coefficients obtained by these two methods are shown in Table 3.
For 885 test data of 6 soil samples, the methods of NCHRP [11], ZHANG et al [15], traditional ANN approach and the ANN approach in this study were used to obtain the predicted and measured values of resilient modulus. Comparisons between measured and predicted MR values were shown in Figures 7-9. Significant differences in accuracy were observed between the traditional prediction model, traditional ANN approach and the ANN approach in this study. It is obvious that the MR values predicted by the ANN approach matched very well with the measured results. It is worth noting that traditional ANN approach method has great instability, which is mainly reflected in the estimation of different soil samples and the outputs of every time the program runs. Figure 9 depicts that R2 are all over 0.98; the RMSE are in the range of 0.96-3.03; and the prediction results of selected test data are all near the equality line, which indicates that the prediction method established in this study has higher prediction accuracy and stronger generalization ability. Therefore, compared with the traditional ANN estimation method, the optimized ANN method of this study has higher accuracy and stability. And it also has the advantages of fast speed, strong generalization ability, great stability and good accuracy, compared with the cumbersome process of model establishing and parameter fitting in the traditional estimation model. Summing up the above, the optimized ANN method is suitable for subgrade soils to accurately determine the resilient modulus.
Table 3 Regression coefficients of different soils
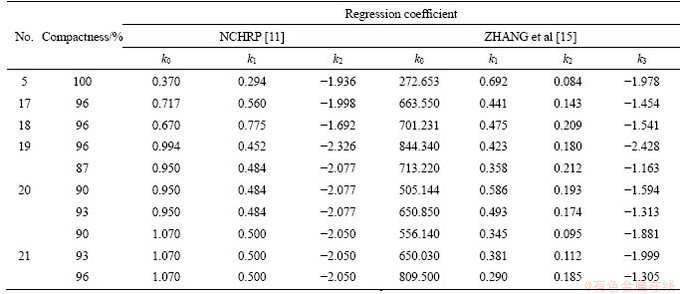
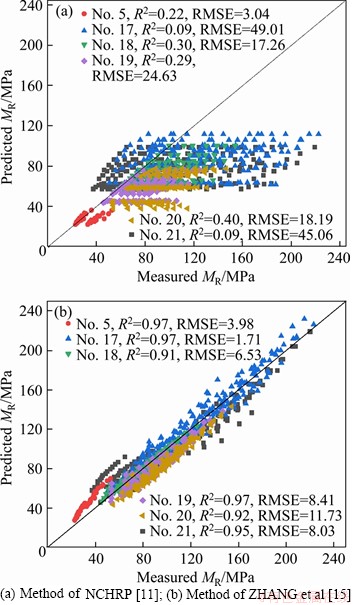
Figure 7 Comparison of measured versus predicted resilient modulus using traditional model:
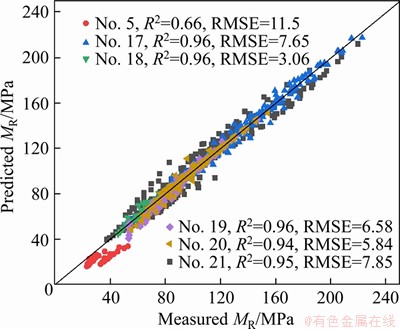
Figure 8 Comparison of measured versus predicted resilient modulus using traditional ANN approach
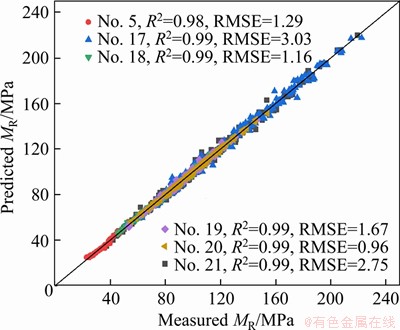
Figure 9 Comparison of measured versus predicted resilient modulus using ANN approach in this study
As previously mentioned, through a large database of resilient modulus of subgrade soils, an optimized artificial neural network method can be built by introducing physical properties of soils (ωl, ωp, Ip, P0.075, γdmax, ωopt), state variables (K, ω) and stress variables (θ, σ). The ANN method provides a special functional mapping relationship between the input layer and the output layer, and it cannot give any insight into the complex physical and mechanical relationship between MR and the input parameters. Thus, it is recommended that the input variables at the range of training dataset when using this prediction method. For the engineering site, firstly, the stress state of subgrade soil and its corresponding compaction state and moisture content state are obtained through the pavement design document, and then the physical properties of soils are obtained through the basic physical property tests. Finally, by using the established estimation method, the resilient modulus of subgrade soils is directly obtained at any condition for pavement design.
4 Conclusions
In this study, based on the experimental data collected from existing literature, an efficient and accurate MR prediction method based on the ANN approach and the multi-population genetic algorithm was developed. The major conclusions of this study can be summarized as follows:
1) A three-layered ANN method optimized by MPGA was established to estimate resilient modulus for subgrade soils. Input variables include ωl, ωp, Ip, P0.075, γdmax, ωopt, K, ω, θ and σ. The output variable is MR.
2) The prediction method based on ANN approach was evaluated by different types of soil. The result shows that the estimation accuracy has a positive correlation with the number of data sets.
3) The relative importance of each input variable of the ANN method was calculated. The most significant parameters are physical properties, followed by state variables, stress variables, respectively.
4) Compared with the traditional resilient modulus prediction model, the prediction method based on ANN approach can be applied to predict the resilient modulus directly instead of predicting the model coefficients of a specific model, saving complicated parameter fitting and calculation process.
5) The prediction method based on ANN approach presented a higher prediction accuracy and stability compared with the latest and classic representative models of the existing literature and traditional ANN approach. The coefficients of determination of 6 kinds of soil samples randomly selected range from 0.98 to 0.99.
6) The ANN method cannot explain the physics and mechanics relationship between input variables and MR. Therefore, it is not recommended to use it as a prediction method when the input variables out of the range of training dataset.
Contributors
The main innovation point of this paper was developed by ZHANG Jun-hui, PENG Jun-hui and ZHOU Chao. The Matlab software was used to establish the ANN estimation method by FAN Hai-shan. PENG Jun-hui and HU Jian-kun collected the data and analyzed it. HU Jian-kun is responsible for writing the initial draft of the manuscript. All authors replied to reviewers’comments and revised the final version.
Conflict of interest
ZHANG Jun-hui, HU Jian-kun, PENG Jun-hui, FAN Hai-shan and ZHOU Chao declare that they have no conflict of interest.
References
[1] ZHANG Jun-hui, PENG Jun-hui, ZHENG Jian-long, DAI Liang-liang, YAO Yong-sheng. Prediction of resilient modulus of compacted cohesive soils in South China [J]. International Journal of Geomechanics, 2019, 19(7): 04019068. DOI: 10.1061/(asce)gm.1943-5622.0001446.
[2] ZHAO Yang, LU Zheng, YAO Hai-lin, GU Fan, DUAN Ya-hui. Experimental study of dynamic resilient modulus of subgrade soils under coupling of freeze-thaw cycles and dynamic load [J]. Journal of Central South University, 2020, 27(7): 2043-2053. DOI: 10.1007/s11771-020-4429-4.
[3] YAN Ke-zhen, XU Hong-bin, SHEN Guang-hui. Novel approach to resilient modulus using routine subgrade soil properties [J]. International Journal of Geomechanics, 2014, 14(6): 04014025. DOI: 10.1061/(asce)gm.1943-5622.000 0369.
[4] AASHTO. Standard method of test for determining the resilient modulus of soils and aggregate materials [S]. Washington, DC: AASHTO, 2003.
[5] AASHTO. Guide for mechanistic-empirical design of new and rehabilitated pavement structures [S]. Washington, DC: AASHTO, 2004.
[6] ZHANG Jun-hui, PENG Jun-hui, ZHENG Jian-long. Progress and prospect of the prediction model of the resilient modulus of subgrade soils [J]. China Journal of Highway and Transport, 2020, 33(1): 1-13. DOI: 10.19721/j.cnki.1001-7372.2020.01.001. (in Chinese)
[7] SEED H B, CHAN C K, LEE C E. Resilience characteristics of subgrade soils and their relation to fatigue failures in asphalt pavements [C]// International Conference on the Structural Design of Asphalt Pavements. Ann Arbor, University of Michigan, 1962: 77-113.
[8] SEED H B, MITRY F G, MONISMITH C L, CHAN C K. Prediction of flexible pavement deflections from laboratory repeated-load tests [R]. Washington, DC: Transportation Research Board, 1967.
[9] UZAN J. Characterization of granular material [M]. Washington, DC: Transportation Research Record, 1985: 52-59.
[10] WITCZAK M W, UZAN J. The universal airport pavement design system, Report I of IV: Granular material characterization [R]. University of Maryland, College Park, MD, 1988.
[11] NCHRP. Harmonized test methods for laboratory determination of resilient modulus for flexible pavement design [S]. Washington, DC: NCHRP, 2003.
[12] AZAM A M, CAMERON D A, RAHMAN M M. Model for prediction of resilient modulus incorporating matric suction for recycled unbound granular materials [J]. Canadian Geotechnical Journal, 2013, 50(11): 1143-1158. DOI: 10.1139/cgj-2012-0406.
[13] QIAN Jin-song, LI Jia-yang, ZHOU Ding, LING Jian-ming. Prediction model of resilient modulus for unsaturated clay soils considering the effect of matric suction [J]. Rock and Soil Mechanics, 2018, 39(1): 123-128. DOI: 10.16285/j.rsm. 2016.0239. (in Chinese)
[14] ZHANG Jun-hui, PENG Jun-hui, ZHENG Jian-long, YAO Yong-sheng. Characterisation of stress and moisture-dependent resilient behaviour for compacted clays in South China [J]. Road Materials and Pavement Design, 2020, 21(1): 262-275. DOI: 10.1080/14680629.2018.1481138.
[15] ZHANG Jun-hui, PENG Jun-hui, ZENG Ling, LI Jue, LI Feng. Rapid estimation of resilient modulus of subgrade soils using performance-related soil properties [J]. International Journal of Pavement Engineering, 2019. DOI: 10.1080/ 10298436.2019.1643022.
[16] YAO Yong-sheng, ZHENG Jian-long, ZHANG Jun-hui, PENG Jun-hui, LI Jue. Model for predicting resilient modulus of unsaturated subgrade soils in South China [J]. KSCE Journal of Civil Engineering, 2018, 22(6): 2089-2098. DOI: 10.1007/s12205-018-1703-1.
[17] SAHA S, GU Fan, LUO Xue, LYTTON R L. Use of an artificial neural network approach for the prediction of resilient modulus for unbound granular material [J]. Transportation Research Record: Journal of the Transportation Research Board, 2018, 2672(52): 23-33. DOI: 10.1177/0361198118756881.
[18] KIM S H, YANG Ji-dong, JEONG J H. Prediction of subgrade resilient modulus using artificial neural network [J]. KSCE Journal of Civil Engineering, 2014, 18(5): 1372-1379. DOI: 10.1007/s12205-014-0316-6.
[19] NAZZAL M D, TATARI O. Evaluating the use of neural networks and genetic algorithms for prediction of subgrade resilient modulus [J]. International Journal of Pavement Engineering, 2013, 14(4): 364-373. DOI: 10.1080/ 10298436.2012.671944.
[20] WANG Xiao-kai, HUA Lin, WANG Xiao-xuan, MEI Xue-song, ZHU Qian-hao, DAI Yu-tong. Soft measurement model of ring's dimensions for vertical hot ring rolling process using neural networks optimized by genetic algorithm [J]. Journal of Central South University, 2017, 24(1): 17-29. DOI: 10.1007/s11771-017-3404-1.
[21] SADROSSADAT E, GHORBANI B, ZOHOURIAN B, KABOUTARI M, RAHIMZADEH OSKOOEI P. Predictive modelling of the MR of subgrade cohesive soils incorporating CPT-related parameters through a soft-computing approach [J]. Road Materials and Pavement Design, 2020, 21(3): 701-719. DOI: 10.1080/14680629.2018.1527241.
[22] SADROSSADAT E, HEIDARIPANAH A, OSOULI S. Prediction of the resilient modulus of flexible pavement subgrade soils using adaptive neuro-fuzzy inference systems [J]. Construction and Building Materials, 2016, 123: 235-247. DOI: 10.1016/j.conbuildmat.2016.07.008.
[23] GOPALAKRISHNAN K. Neural network–swarm intelligence hybrid nonlinear optimization algorithm for pavement moduli back-calculation [J]. Journal of Transportation Engineering, 2010, 136(6): 528-536. DOI: 10.1061/(asce)te.1943-5436.0000128.
[24] MCCULLOCH W S, PITTS W. A logical calculus of the ideas immanent in nervous activity [J]. Bulletin of Mathematical Biology, 1990, 52(1, 2): 99-115. DOI: 10.1016/S0092-8240(05)80006-0.
[25] NIELSEN M. Neural networks and deep learning [M]. San Francisco, CA, USA: Determination Press, 2015.
[26] RUMELHART D E, HINTON G E, WILLIAMS R J. Learning representations by back-propagating errors [J]. Nature, 1986, 323(6088): 533-536. DOI: 10.1038/323533a0.
[27] PENG Jun-hui, ZHANG Jun-hui, LI Jue, YAO Yong-sheng, ZHANG An-shun. Modeling humidity and stress-dependent subgrade soils in flexible pavements [J]. Computers and Geotechnics, 2020, 120: 103413. DOI: 10.1016/ j.compgeo.2019.103413.
[28] ZHANG Jun-hui, LI Feng, ZENG Ling, PENG Jun-hui, LI Jue. Numerical simulation of the moisture migration of unsaturated clay embankments in Southern China considering stress state [J]. Bulletin of Engineering Geology and the Environment, 2021, 80(1): 11-24. DOI:10.1007/s10064-020-01916-6.
[29] ZIDAN A F, ABOUKHADRA A A, GABER Y. Enhancement of resilient modulus of cohesive soil using an enzymatic preparation [J]. Journal of Central South University, 2019, 26(9): 2596-2608. DOI: 10.1007/s11771-019-4197-1.
[30] ZHANG Jun-hui, PENG Jun-hui, ZHANG An-shun, LI Jue. Prediction of permanent deformation for subgrade soils under traffic loading in Southern China [J]. International Journal of Pavement Engineering, 2020: 1-10. DOI: 10.1080/ 10298436.2020.1765244.
[31] YANG Shu-rong, HUANG Wei-hsing, TAI Yu-tsung. Variation of resilient modulus with soil suction for compacted subgrade soils [J]. Journal of the Transportation Research Board, 2005, 1913(1): 99-106. DOI: 10.1177/036119810 5191300110.
[32] ZHANG Shi-ping, PAK R Y S, ZHANG Jun-hui. Vertical time-harmonic coupling vibration of an impermeable, rigid, circular plate resting on a finite, poroelastic soil layer [J]. Acta Geotechnica, 2020. DOI: 10.1007/s11440-020-01067-8.
[33] SHI Feng, WANG Xiao-chuan, YU Lei, LI Yang. MATLAB neural network analysis of 30 cases [M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2010. (in Chinese)
[34] ZIAEE S A, SADROSSADAT E, ALAVI A H, MOHAMMADZADEH SHADMEHRI D. Explicit formulation of bearing capacity of shallow foundations on rock masses using artificial neural networks: Application and supplementary studies [J]. Environmental Earth Sciences, 2015, 73(7): 3417-3431. DOI: 10.1007/s12665-014-3630-x.
[35] ALAVI A H, GANDOMI A H. Prediction of principal ground-motion parameters using a hybrid method coupling artificial neural networks and simulated annealing [J]. Computers & Structures, 2011, 89(23, 24): 2176-2194. DOI: 10.1016/ j.compstruc.2011.08.019.
[36] VADOOD M, JOHARI M S, RAHAI A R. Relationship between fatigue life of asphalt concrete and polypropylene/polyester fibers using artificial neural network and genetic algorithm [J]. Journal of Central South University, 2015, 22(5): 1937-1946. DOI: 10.1007/s11771-015-2713-5.
[37] AGHAJANI H F, YENGEJEH M G, KARIMZADEH A, SOLTANI-JIGHEH H. A new procedure for determining dry density of mixed soil containing oversize gravel [J]. Journal of Central South University, 2018, 25(12): 2841-2856. DOI: 10.1007/s11771-018-3957-7.
[38] LIANG Yue-ji, REN Chao, WANG Hao-yu, HUANG Yi-bang, ZHENG Zhong-tian. Research on soil moisture inversion method based on GA-BP neural network model [J]. International Journal of Remote Sensing, 2019, 40(5, 6): 2087-2103. DOI: 10.1080/01431161.2018.1484961.
[39] GUPTA S, RANAIVOSON A, EDIL T, BENSON C, SAWANGSURIYA A. Pavement design using unsaturated soil technology [R]. Minnesota Dept. of Transportation, St. Paul, MN, 2007.
[40] LIANG R Y, RABAB’AH S, KHASAWNEH M. Predicting moisture-dependent resilient modulus of cohesive soils using soil suction concept [J]. Journal of Transportation Engineering, 2008, 134(1): 34-40. DOI: 10.1061/(asce)0733-947x(2008) 134: 1(34).
[41] LAN Wei. Unsaturated characteristics and resilient modulus prediction model of subgrade soil [D]. Shanghai: Tongji University, 2009. (in Chinese)
[42] QIU Xin, QIAN Jin-song, ZHANG Shi-zhou. Research on prediction model of dynamic resilient modulus of subgrade soil based on matric suction [J]. Hydrogeology and Engineering Geology, 2011, 38(3): 49-90. DOI: 10.16030/j.cnki.issn.1000-3665.2011.03.017. (in Chinese)
[43] NG C W W, ZHOU C, YUAN Q, XU J. Resilient modulus of unsaturated subgrade soil: Experimental and theoretical investigations [J]. Canadian Geotechnical Journal, 2013, 50(2): 223-232. DOI: 10.1139/cgj-2012-0052.
[44] HAN Zhong, VANAPALLI S K. Relationship between resilient modulus and suction for compacted subgrade soils [J]. Engineering Geology, 2016, 211: 85-97. DOI: 10.1016/ j.enggeo.2016.06.020.
[45] HAN Zhong, VANAPALLI S K, ZOU Wei-lie. Integrated approaches for predicting soil-water characteristic curve and resilient modulus of compacted fine-grained subgrade soils [J]. Canadian Geotechnical Journal, 2017, 54(5): 646-663. DOI: 10.1139/cgj-2016-0349.
[46] LIU Wei-zheng, ZENG Yi-jun, YAO Yong-sheng, ZHANG Jun-hui. Experimental study and prediction model of dynamic resilient modulus of compacted subgrade soils subjected to moisture variation [J]. Chinese Journal of Geotechnical Engineering, 2019, 41(1): 175-183. (in Chinese)
[47] HEDAYAT A A, AHMADI AFZADI E, KALANTARIPOUR H, MORSHEDI E, IRANPOUR A. A new predictive model for the minimum strength requirement of steel moment frames using artificial neural network [J]. Soil Dynamics and Earthquake Engineering, 2019, 116: 69-81. DOI: 10.1016/j.soildyn.2018.09.046.
[48] TCHABAN T, TAYLOR M J, GRIFFIN J P. Establishing impacts of the inputs in a feedforward neural network [J]. Neural Computing & Applications, 1998, 7(4): 309-317. DOI: 10.1007/BF01428122.
[49] GEVREY M, DIMOPOULOS I, LEK S. Two-way interaction of input variables in the sensitivity analysis of neural network models [J]. Ecological Modelling, 2006, 195(1, 2): 43-50. DOI: 10.1016/j.ecolmodel.2005.11.008.
[50] LEONG H Y, ONG D E L, SANJAYAN J G, NAZARI A, KUEH S M. Effects of significant variables on compressive strength of soil-fly ash geopolymer: Variable analytical approach based on neural networks and genetic programming [J]. Journal of Materials in Civil Engineering, 2018, 30(7): 04018129. DOI: 10.1061/(asce)mt.1943-5533.0002246.
(Edited by ZHENG Yu-tong)
中文导读
基于人工神经网络的路基土回弹模量预估方法
摘要:回弹模量作为路基结构的刚度指标,是路面结构设计中的重要参数。为快速准确地获取路基土回弹模量,本文采用BP神经网络对回弹模量进行直接预估,以多种群遗传算法对BP算法进行优化,解决了传统BP神经网络效率低、易陷于局部最优和过拟合等问题。建立了由10个输入变量、21个隐含层和1个输出变量组成的回弹模量预估方法。其中,输入变量包括路基土的物性参数(液限、塑限、塑性指数、细粒含量、最大干密度、最佳含水率)、状态变量(压实度、含水率)和应力变量(围压、偏应力);输出变量为回弹模量。结合已有文献中的大量试验数据,将所建立的优化神经网络方法与现有代表性的预估模型进行对比分析。研究结果表明,相比于传统预估模型,基于多种群遗传算法优化的BP神经网络预估方法在回弹模量预估中具有速度快、泛化能力强和预估精度高等优点。
关键词:回弹模量;路基土;人工神经网络;多种群遗传算法;预估方法
Foundation item: Project(51878078) supported by the National Natural Science Foundation of China; Project(2018-025) supported by the Training Program for High-level Technical Personnel in Transportation Industry, China; Project(CTKY-PTRC-2018-003) supported by the Design Theory, Method and Demonstration of Durability Asphalt Pavement Based on Heavy-duty Traffic Conditions in Shanghai Area, China
Received date: 2020-09-27; Accepted date: 2021-01-08
Corresponding author: PENG Jun-hui, PhD; Tel: +86-15974146231; E-mail: pjh@stu.csust.edu.cn; ORCID: https://orcid.org/0000-0002-8890-5343
Abstract: The resilient modulus (MR) of subgrade soils is usually used to characterize the stiffness of subgrade and is a crucial parameter in pavement design. In order to determine the resilient modulus of compacted subgrade soils quickly and accurately, an optimized artificial neural network (ANN) approach based on the multi-population genetic algorithm (MPGA) was proposed in this study. The MPGA overcomes the problems of the traditional ANN such as low efficiency, local optimum and over-fitting. The developed optimized ANN method consists of ten input variables, twenty-one hidden neurons, and one output variable. The physical properties (liquid limit, plastic limit, plasticity index, 0.075 mm passing percentage, maximum dry density, optimum moisture content), state variables (degree of compaction, moisture content) and stress variables (confining pressure, deviatoric stress) of subgrade soils were selected as input variables. The MR was directly used as the output variable. Then, adopting a large amount of experimental data from existing literature, the developed optimized ANN method was compared with the existing representative estimation methods. The results show that the developed optimized ANN method has the advantages of fast speed, strong generalization ability and good accuracy in MR estimation.


