网络首发时间: 2018-04-18 17:49

稀有金属2019年第3期

基于应变补偿的含稀土Ti₂AlNb基合金高温本构模型

周峰 王克鲁 鲁世强 任书杰 陈虚怀 万鹏

南昌航空大学航空制造工程学院

摘 要：

利用Gleeble-3500热模拟试验机对Ti-22Al-24Nb-0.5Y合金试样进行等温恒应变速率压缩试验, 采用摩擦及温度对试验数据进行修正, 通过多元线性回归拟合的材料参数与应变量多项式函数关系, 构建了基于应变补偿的Ti-22Al-24Nb-0.5Y合金本构模型。结果表明:摩擦及温度修正的流动应力更能够真实反映合金在高温变形过程中的动态响应;经摩擦修正后的流动应力均低于实验测得的流动应力, 随温度的升高, 摩擦修正的流动应力越接近于实测值;在低温高应变速率条件下, 温升引起的流动应力变化较大, 在低应变速率条件下和变形温度高于1050℃时, 温升引起的流动应力变化较小。以应变为4次多项式拟合得到的本构模型能够较好预测热压缩模拟过程中流动应力, 其相关系数R达到0.9907, 平均相对误差E为4.79%。该模型可作为Ti₂AlNb基合金塑性成形过程中有限元模拟的本构关系。

关键词：

Ti-22Al-24Nb-0.5Y合金;摩擦修正;温度修正;应变量补偿;本构模型;

中图分类号： TG146.23;V252

作者简介：周峰 (1992-) , 男, 河南信阳人, 硕士研究生, 研究方向:金属材料微观结构调控研究, E-mail:13207090876@163.com;*王克鲁, 教授;电话:13133804266;E-mail:wangkelu@126.com;

收稿日期：2018-03-13

基金：国家自然科学基金项目 (51464035) 资助;

High Temperature Constitutive Model of Rare Earth Ti₂AlNb Based Alloy Based on Strain Compensation

Zhou Feng Wang Kelu Lu Shiqiang Ren Shujie Chen Xuhuai Wan Peng

Institute of Aeronautical Manufacturing Engineering, Nanchang Hangkong University

Abstract：

Isothermal constant strain rate compression tests were carried out for samples of Ti-22 Al-24 Nb-0.5 Y alloy by Gleeble-3500 thermal simulator, and correction of test data by friction and temperature and the constitutive model of Ti-22 Al-24 Nb-0.5 Y alloy based on the strain compensation were constructed by the relation between the material parameters and the polynomial function of the variable linear regression. The results showed that the flow stress corrected by friction and temperature could reflect the dynamic response of the alloy in the process of high temperature deformation; the flow stress after friction correction was lower than the experimentally measured flow stress, with the increase of temperature, the frictional corrected flow stress was closer to the measured value; under the condition of low temperature and high strain rate, the flow stress caused by temperature rise was larger, under low strain rate conditions and deformation temperature higher than 1050 ℃, the change of flow stress caused by temperature rise was small. The constitutive model based on strain 4 polynomial fitting could better predict the flow stress in the simulation of thermal compression, and the correlation coefficient R was 0.9907, and the average relative error E was 4.79%. The model could be used as the constitutive relation of the finite element simulation in the plastic forming process of Ti₂AlNb based alloy.

Keyword：

Ti-22Al-24Nb-0.5Y alloy; friction correction; temperature correction; strain compensation; constitutive model;

Received： 2018-03-13

Ti₂AlNb基合金是Ti-Al系金属间化合物的一种, 与镍基合金相比, 密度小, 约为镍基合金的一半, 有利于设备重量的减轻, 提高发动机效率; 与陶瓷材料相比, 在高温下具有一定的塑性, 与传统的TiAl基合金和Ti₃Al基合金相比, 尽管Ti₂AlNb基合金的密度略大, 但其具备更高的比强度、 优良的抗蠕变能力和良好的可成形性 ^[1,2,3,4] 。 Ti₂AlNb基合金作为600～800 ℃温度范围内的潜在高温结构材料, 被认为是航空领域的高端结构材料, 其极具开发潜力及应用前景, 在航空航天领域的应用也越来越广泛 ^[5,6] 。 但Ti₂AlNb基合金属难变形材料 ^[7,8] , 其力学性能及组织对变形工艺参数较为敏感, 了解其热加工条件下的变形特点, 可为合金在热加工工艺的制订提供参考。 因此, 建立拟合精度较高的本构关系模型对合金的基础研究具有重要的意义。

材料的流动应力本构模型是指材料流动应力和热力参数或状态参数之间的函数关系 ^[9] , 在材料塑性变形的有限元数值模拟应用上较为重要。 目前, 许多学者研究材料的本构模型多采用传统的Arrhenius型方程中的双曲正弦函数建立本构模型, 通过Arrhenius型方程推导和计算出材料在热变形过程中流变应力与应变速率和变形温度的线性关系 ^[10,11] 。 但该模型未考虑应变量对流动应力及材料参数的影响, 无法全面准确的反映出热变形条件对合金热变形过程的影响。 为此, 国内外学者考虑应变量对材料热变形行为的影响, 建立了一些材料的本构关系模型, 均取得了较为理想的预期效果 ^[12,13,14] 。

本研究以Ti-22Al-24Nb-0.5Y合金热压缩模拟试验获得的数据为基础, 为防止试验产生误差, 影响合金本构模型的预测精确度, 采用摩擦及温度对试验数据进行修正, 然后利用多元线性回归拟合建立材料参数与应变量的多项式函数, 充分考虑应变量对Ti₂AlNb基合金合金热变形行为的影响, 建立基于应变量补偿的本构模型, 重在为Ti₂AlNb基合金的热成形工艺及有限元数值模拟提供参考。

1 实 验

试验材料为铸态Ti₂AlNb基合金, 其原始组织如图1所示, 其名义成分为Ti-22Al-24Nb-0.5Y, 从图1中可以看到, 弥散分布的白色颗粒物和α₂/O相层片组织分布在B2相基体中, 经能谱 (EDS) 分析, 白色颗粒物为Y₂O₃稀土相, 其中α₂/O相层片尺寸约5～15 μm, 稀土相颗粒尺寸约1～3 μm。 热压缩试样尺寸为Φ8 mm×12 mm的圆柱体, 利用Gleeble-3500热模拟试验机进行等温恒应变速率压缩试验。 热压缩变形温度为900, 930, 960, 990, 1020, 1050, 1080和1100 ℃; 应变速率为0.001, 0.010, 0.100, 1.000和10.000 s^-1; 高度压下量为70%, 对应的真应变为1.2, 以5 ℃·s^-1加热至设定的变形温度后保温300 s, 为使试样内部组织温度均匀, 压缩结束后立即水冷。

图1Ti-22Al-24Nb-0.5Y合金原始组织的扫描电镜 (SEM) 图像

Fig.1 SEM image of original microstructure of Ti-22Al-24Nb-0.5Y alloy

2 流动应力曲线修正及分析

2.1 摩擦修正

在Gleeble-3500热模拟试验机压缩圆柱体变形过程中, 试样端头与压头之间存在摩擦, 因此压缩变形后的试样呈鼓形, 然而热模拟试验机实验过程应力的计算实际是完全按照无摩擦来进行输出的, 为了真实反映材料在动态高温变形过程中的动态响应, 需要对热压缩实验数据进行摩擦修正, 流变应力摩擦修正采用如下公式 ^[15] :

σ=σ0(2mRh)22[exp(2mRh)-2mRh-1]?????????(1) σ=σ0(2mRh)22[exp(2mRh)?2mRh?1]?????????(1)

式中, m为摩擦因子, 采用下式进行计算 ^[16] :

m=Rb/Η4√3-2√3b/9?????????(2)b=4ΔRR?ΗΔΗ?????????(3)ΔR=RΜ-RΤ=RΜ-√3h0R20Η-2R2Μ?????????(4)

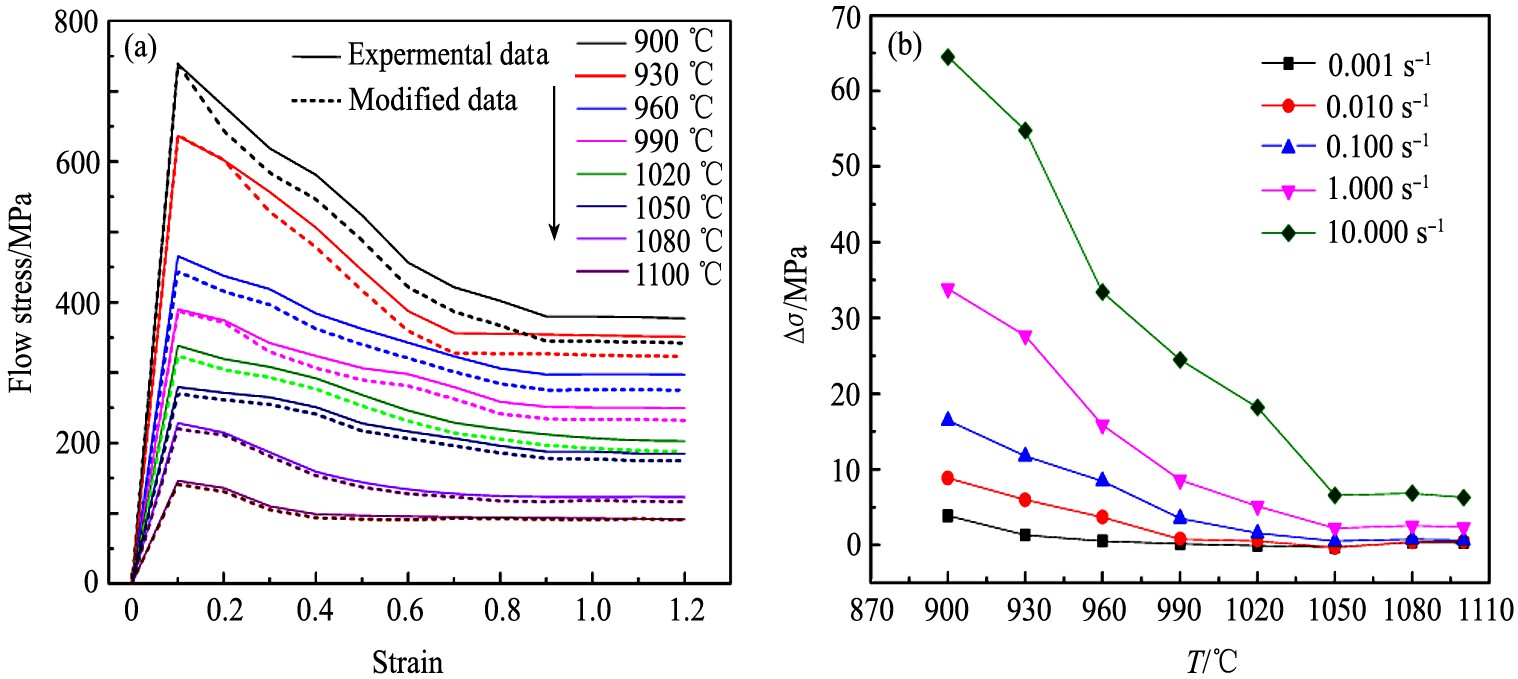
式中, H为变形结束后的试样高度; R₀为试样的原始半径4 mm; R_M为变形结束后的试样半径; R_T为与压头接触的试样底面半径。 图2 (a) 为应变1.0 s^-1时的流变应力实验值与摩擦修正后的流变应力值对比。 从图2 (a) 可以看出, 经摩擦修正的流动应力均低于实验测得的流动应力; 随温度的升高, 摩擦修正的流动应力越接近于实测值。

2.2 温度修正

利用热模拟试验机进行热压缩试验时, 测得试样表面温度为变形温度, 但试样在变形过程中的温度是变化的, 其受到的塑性变形功约90%都转化为变形热, 在较高应变速率条件下, 变形的时间较短, 变形处于或趋近于绝热状态, 导致这部分能量不能及时向周围散失, 即热压缩过程产生了温升与散热效应。 因此试样在受温升与散热效应的影响, 可能导致高应变速率条件下合金的实际变形温度高于理论温度或低应变速率条件下的实际变形温度低于理论温度等。 本研究采用式 (5) 计算热压缩过程中的升温。

ΔΤ=Ρ/Cε∫0σdε?????????(5)

式中, ΔT为材料变形时所引起的温升 (℃) , P为与应变速率有关的热转换系数, C为材料的热容系数 (N·mm^-2·℃^-1) , 该实验选取热容系数C=4 ^[17] 。 其中

{Ρ=0????˙ε<0.001s-1Ρ=1+˙ε3???0.001s-1≤˙ε≤1.000s-1Ρ=1???˙ε>1.000s-1?????????(6)

由温升引起的流变应力的变化可由式 (7) 表示 ^[18] :

Δσ=ΔΤdσdΤ?????????(7)

式中, Δσ是由温升引起的流动应力变化值, dσ/dT为经摩擦修正的流动应力σ与T (实验温度+温升) 的斜率。 图2 (b) 为温升引起的流变应力变化的最大值。 从图2 (b) 可以看出, 在应变速率为10.000 s^-1、 变形温度为900 ℃条件下, 温升引起的流动应力变化最大值达到64.37 MPa, 说明温升对流动应力的影响不可忽视; 在低温高应变速率条件下, 温升引起的流动应力变化较大; 在0.001, 0.010 s^-1条件下, 温升引起的流动应力变化较小; 在高于1050 ℃时, 温升引起的流动应力变化较小。

2.3 流变应力分析

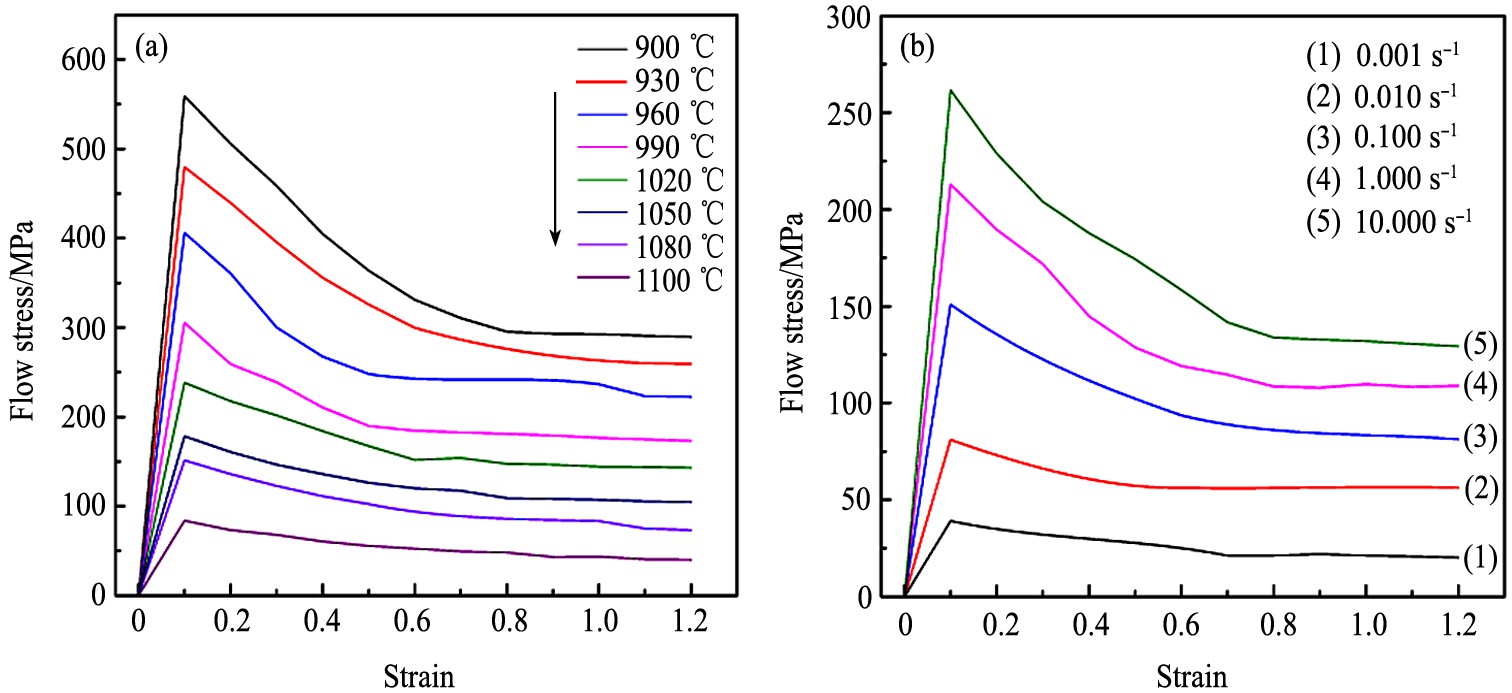
图3为Ti-22Al-24Nb-0.5Y合金经摩擦和温度修正的不同变形条件下的应力-应变曲线。 在高温压缩变形的初始阶段, 应变硬化占主导作用, 使合金流变应力随应变量的增加而迅速增大; 随压缩变形的继续进行, 软化作用逐步加强, 流变应力到达峰值后, 动态回复和动态再结晶引起的流变软化作用开始大于加工硬化作用, 导致流变应力开始迅速下降, 当变形量达到某一定值时, 加工硬化与动态软化达到动态平衡, 在应力-应变曲线上表现出流变应力随变形量的增加而变化不大。

从图3 (a) 可以看出, 在应变速率为0.100 s^-1条件下, 随变形温度的降低, 流动应力逐渐升高表明合金流动应力对温度的影响较敏感; 在高温下, 合金流动应力-应变曲线为典型的动态回复型, 1100 ℃表现尤为明显。 从图3 (b) 可以看出, 在变形温度为1080 ℃条件下, 随应变速率速率的升高, 合金流动应力越高, 说明合金流动应力对应变速率的影响较为敏感; 在低应变速率下, 合金流动应力到达峰值后, 流动应力随应变量的增加变化不大。

图2 与摩擦及温度修正的相关曲线

Fig.2 Correlation curves with friction and temperature correction

(a) Comparison between flow curve obtained by experiment and friction correction; (b) Maximum change of flow stress caused by temperature rise

图3 不同变形条件下的流动应力曲线

Fig.3 Flow stress curves under different deformation conditions

(a) Strain rate of 0.1 s^-1; (b) Deformation temperature of 1080℃

3 本构关系模型

3.1 传统Arrhenius本构模型

对于不同的材料, 其反映材料动态特性的本构关系相差很大, 流动应力、 应变速率和变形温度之间的关系函数可用Zener和Hollomon提出的Z参数 (温度补偿的应变速率因子) 来优化Arrhenius型方程描述 ^[19] , 该方程有3种表示形式:

Ζ=˙εexp(QRΤ)=A1σn1?????????(8)Ζ=˙εexp(QRΤ)=A2exp(βσ)?????????(9)Ζ=˙εexp(QRΤ)=A3[sinh(ασ)]n?????????(10)

式中, σ为流动应力, MPa; ˙ε 为应变速率, s^-1; Q为热激活能, kJ·mol^-1; R为气体常数 (一般取8.314 J·mol^-1·K^-1) ; T为热力学温度, K; 式中, A₁, A₂, A₃分别为材料常数; n, n₁, α, β表示加工硬化指数, 其中α=β/n₁。 式 (1) 和 (2) 分别适用于高应力水平和低应力水平, 式 (3) 由Sellars和Tegart提出对Arrhenius方程进行双曲正弦修正, 对高应力和低应力水平均适应 ^[20] 。

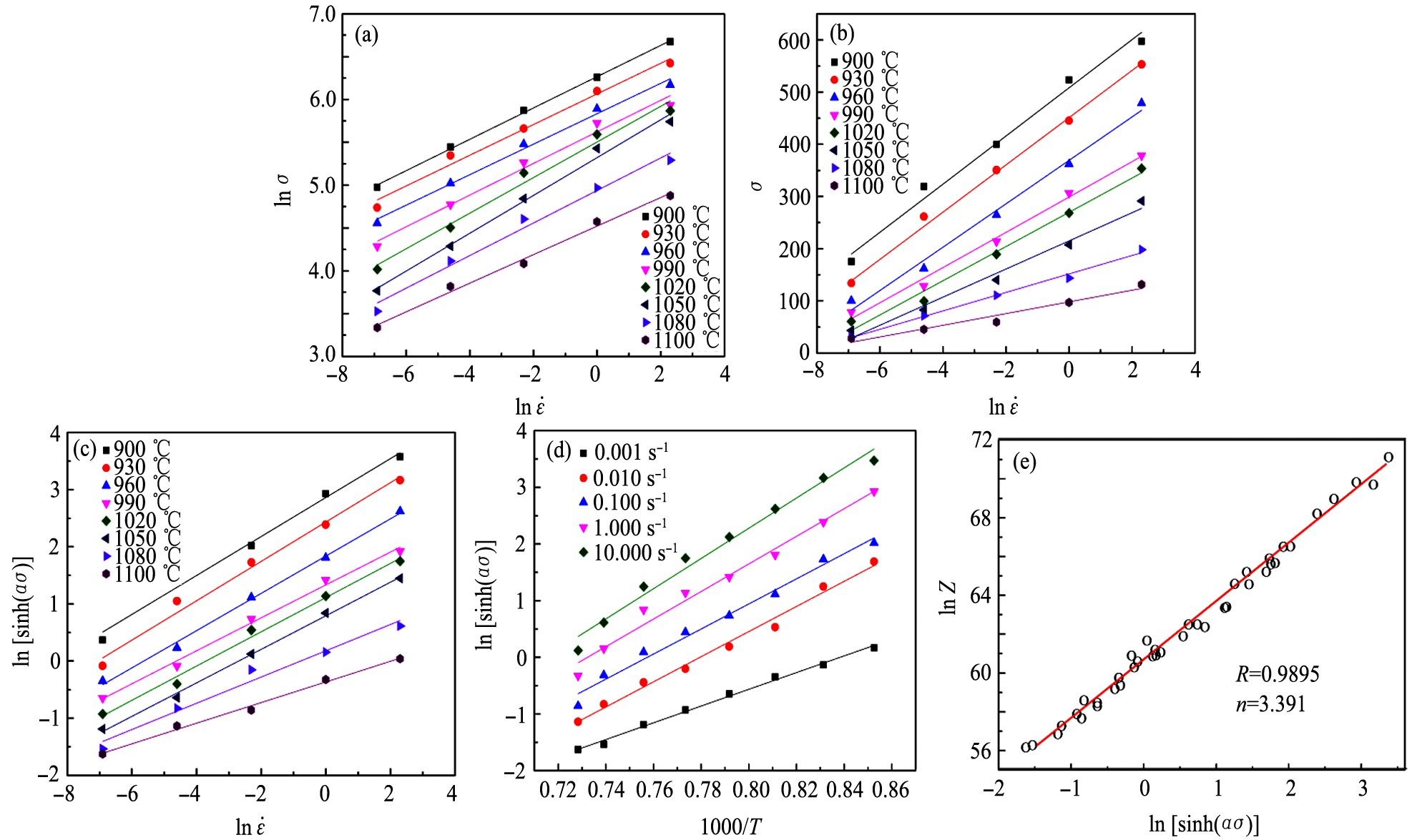
以应变为0.5时的流动应力为例, 建立Ti-22Al-24Nb-0.5Y合金的双曲正弦函数本构方程, 由双曲正弦型函数可知, 需要对待定系数α求解, 首先将式 (8) ～ (10) 两边取对数并整理得式 (11) ～ (13) , 当温度一定时, 将应变量为0.5时经摩擦和温度修正的数据代入式 (11) ～ (12) 进行一元线性拟合, 可获得合 lnσ-ln˙ε 和 σ-ln˙ε 的拟合斜率1/n₁, 1/β, 求得平均值α= (1/n₁) / (1/β) =6.924×10^-3。

lnσ=ln˙εn1+Qn1RΤ-lnA1n1?????????(11)σ=ln˙εβ+QβRΤ-lnA2β?????????(12)ln[sinh(ασ)]=ln˙εn+QnRΤ-lnA3n?????????(13)

当变形温度T恒定时, 对式 (13) 求ln ˙ε 的偏导, 整理得式 (14) , 通过拟合 ln[sinh(ασ)]-ln˙ε 之间的线性关系获得n=3.5的值; 当应变速率一定时, 对式 (14) 求1/T的偏导, 整理得式 (15) 代入拟合ln[sinh (ασ) ]-1/T之间的线性关系获得k=21735.92。

n=?ln˙ε?ln[sinh(ασ)]?????????(14)k=QnR=?ln[sinh(ασ)]?(1/Τ)?????????(15)

故变形激活能表达式:

Q=R[?ln˙ε?ln[sinh(ασ)]]Τ[?ln[sinh(ασ)]?(1/Τ)]˙ε?????????(16)

应变为0.5时的变形激活能为Q=632.494 kJ·mol^-1, 经Z参数优化后的n为3.391, 其截距为lnA为55.394, 通过以上常数n, α, Q, A的计算, 可得Ti-22Al-24Nb-0.5Y合金在应变为0.5下的Ar-rhenius本构方程:

图4 应变为0.5时线性关系拟合

Fig.4 Linear relationships fitting with strain of 0.5

(a) Between lnσand ln

; (b) Betweenσand ln

; (c) Between ln[sinh (ασ) ]and ln

; (d) Between ln[sinh (ασ) ]and 1/T; (e) Between ln Z and ln[sinh (ασ) ]

˙ε=e55.394[sinh(6.924×10-3σ)]3.391exp(-6324948.314Τ)?????????(17)

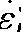
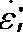
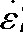
为了验证经Z参数优化的传统Arrhenius本构方程对应变0.5时的流动应力的精确度, 将试验条件代入求得的本构方程中, 计算其预测值, 并与实际值进行比较, 采用相关系数R和平均相对误差E定量描述本构模型的精确度, 公式如下:

R=Ν∑i=1(Ci-ˉC)(Τi-ˉΤ)√Ν∑i=1(Ci-ˉC)2√Ν∑i=1(Τi-ˉΤ)2?????????(18)E=Ν∑i=1|Ci-ΤiCi|×100%Ν?????????(19)

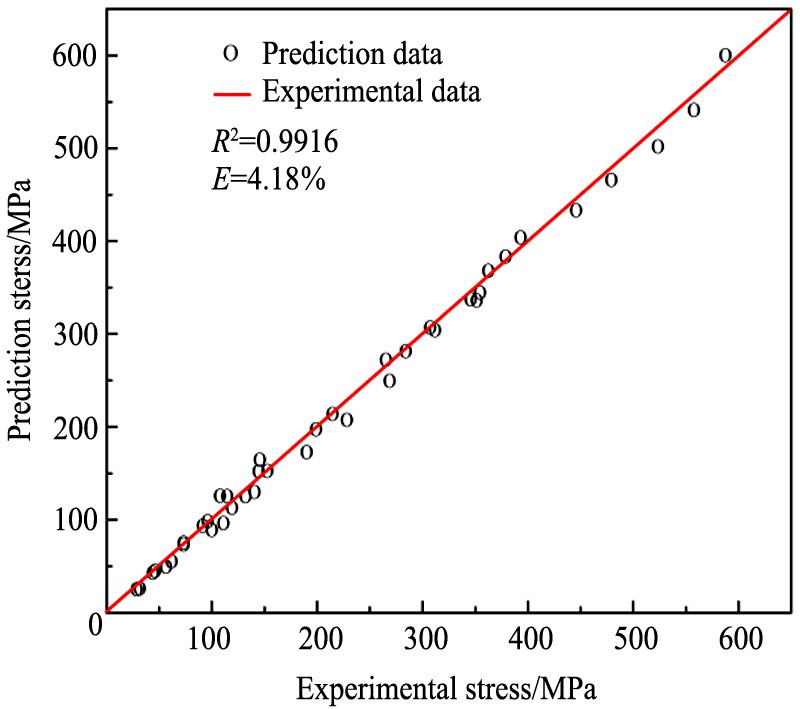
式中, C为实际值, T为预测值, N为数据点个数。 图5为应变为0.5时的预测值与实验值相关性。 经计算得相关系数R为0.9916, 平均相对误差为4.18%, 表明该本构模型能够较好的预测应变为0.5时的流动应力。 虽然该本构模型具有较高的预测精度, 但该本构模型未能考虑应变量对流动应力的影响, 对预测全部的流动应力带来不便。

3.2 基于应变量补偿的Arrhenius本构模型

在塑性变形过程中, 应变对高温流变行为有重要影响, 例如在整个应变范围内, 应变对材料的变形激活能Q和其他材料参数n, α, lnA等的影响, 由图2应力-应变曲线可知, 应变对流动应力有重要的影响, 尤其是在变形过程中流动应力到达峰值应力前的初始阶段。 然而传统的Arrhenius本构模型并未考虑应变量因素的影响, 为了建立较优的本构模型, 需要建立考虑应变补偿的本构模型, 可以通过对不同应变下变形激活能和各材料参数进行多项式拟合来实现。

图5 应变为0.5时的预测值与实验值相关性

Fig.5 Correlation between predicted value and experimental value with strain of 0.5

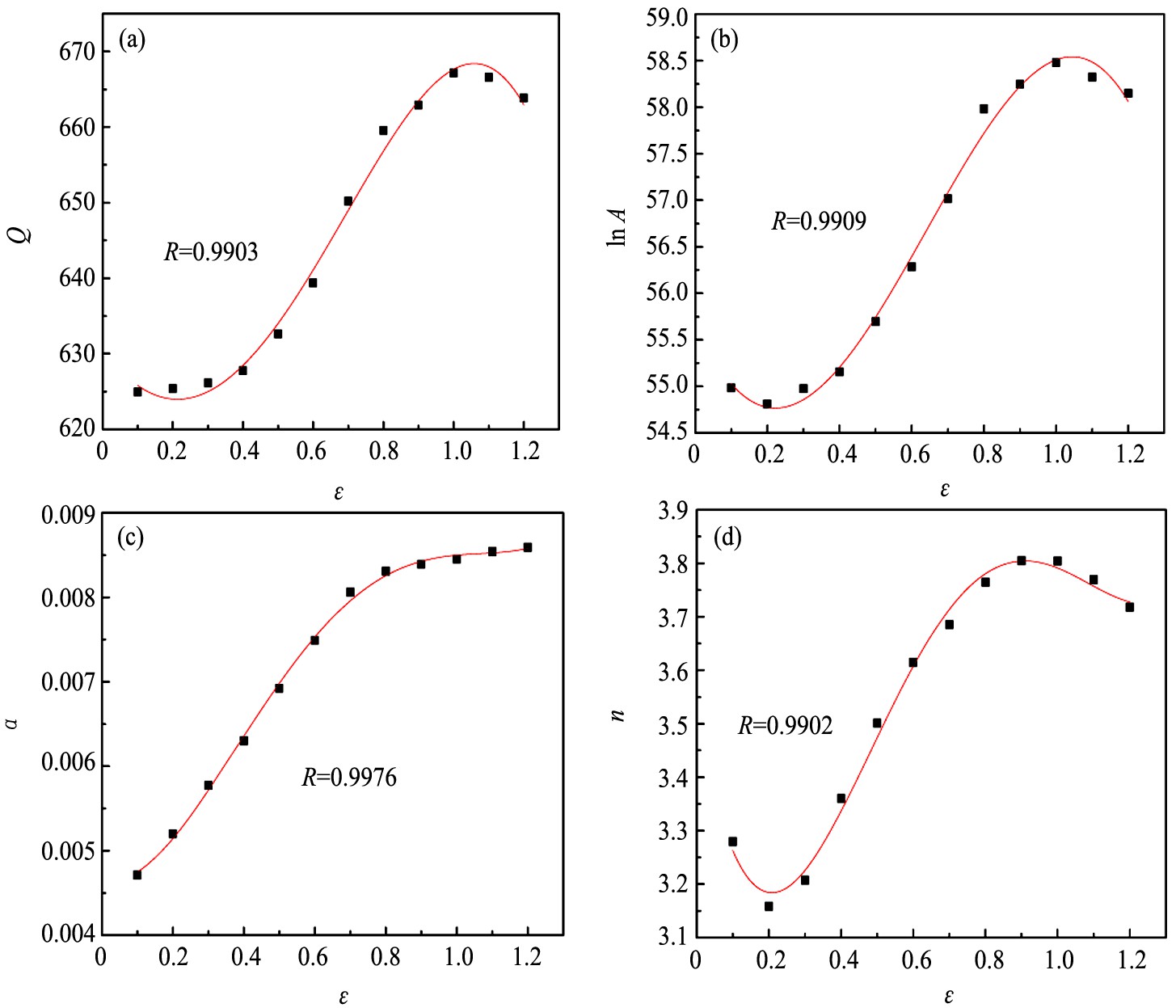
利用传统本构模型, 计算出应变在0.1～1.2, 间隔为0.1条件下的各材料参数Q, n, α, lnA。 通过对数据进行2～8次多项式拟合对比, 发现采用4次多项式拟合精度最高, 表明它们之间存在复杂的非线性关系; 材料常数与应变之间的拟合结果见图6。

{Q=630.4071-59.2992ε+133.8059ε2+33.9849ε3-71.2333ε4lnA=55.6909-8.8713ε+23.7107ε2-10.989ε3-1.031ε4α=0.0046-0.0011ε+0.0227ε2-0.0272ε3+0.0094ε4n=3.5222-3.7224ε+12.5069ε2-12.5018ε3+3.9861ε4?????????(20)

将多元线性回归拟合得到材料变形激活能和各材料参数与应变量的多项式函数 (20) 引入到经Z参数优化的传统Arrhenius本构模型中, 整理后得到基于应变量补偿的本构关系 (21) , 利用该本构模型就可以预测不同应变量、 应变速率和变形温度下的流动应力。

{σ=1αln{(ΖA)1/n+[1+(ΖA)2/n]1/2}Ζ=˙εexp(QRΤ)?????????(21)

3.3 本构模型验证及预测分析

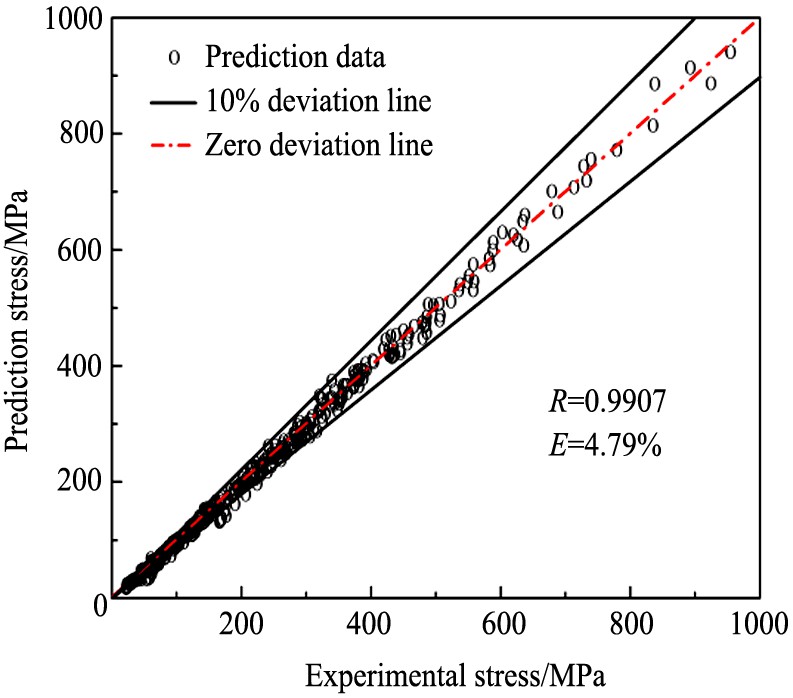
为了验证基于应变补偿的本构模型的精确度, 将实验全部的应变 (应变0.1～1.2, 间隔为0.1) 、 应变速率和变形温度代入基于应变补偿的本构模型中获得预测值, 并与实验值进行对比, 如图7所示, 并根据式 (18) 和 (19) 进行该本构模型的精确度分析, 整理结果如图8所示。

经计算, 该本构模型相关系数R为0.9907, 预测值偏差在10%以内的数据点占96.91%, 平均相对误差E为4.79%, 同时结合图7, 8可以看出, 基于应变补偿的本构模型对流动应力的预测与试验值较为接近, 表明该本构模型具有较高的预测精度。 基于应变补偿的本构模型因考虑了应变对流动应力的影响, 具有较优的预测效果, 优于传统的Arrhenius本构模型, 可合理的应用于优化热加工工艺参数和有限元数值模拟中。

图6 材料参数与应变的多项式线性拟合

Fig.6 Polynomial linear fitting of material parameters and strain

(a) Activation energy Q and ε; (b) lnA and strain; (c) α and strain; (d) n and strain

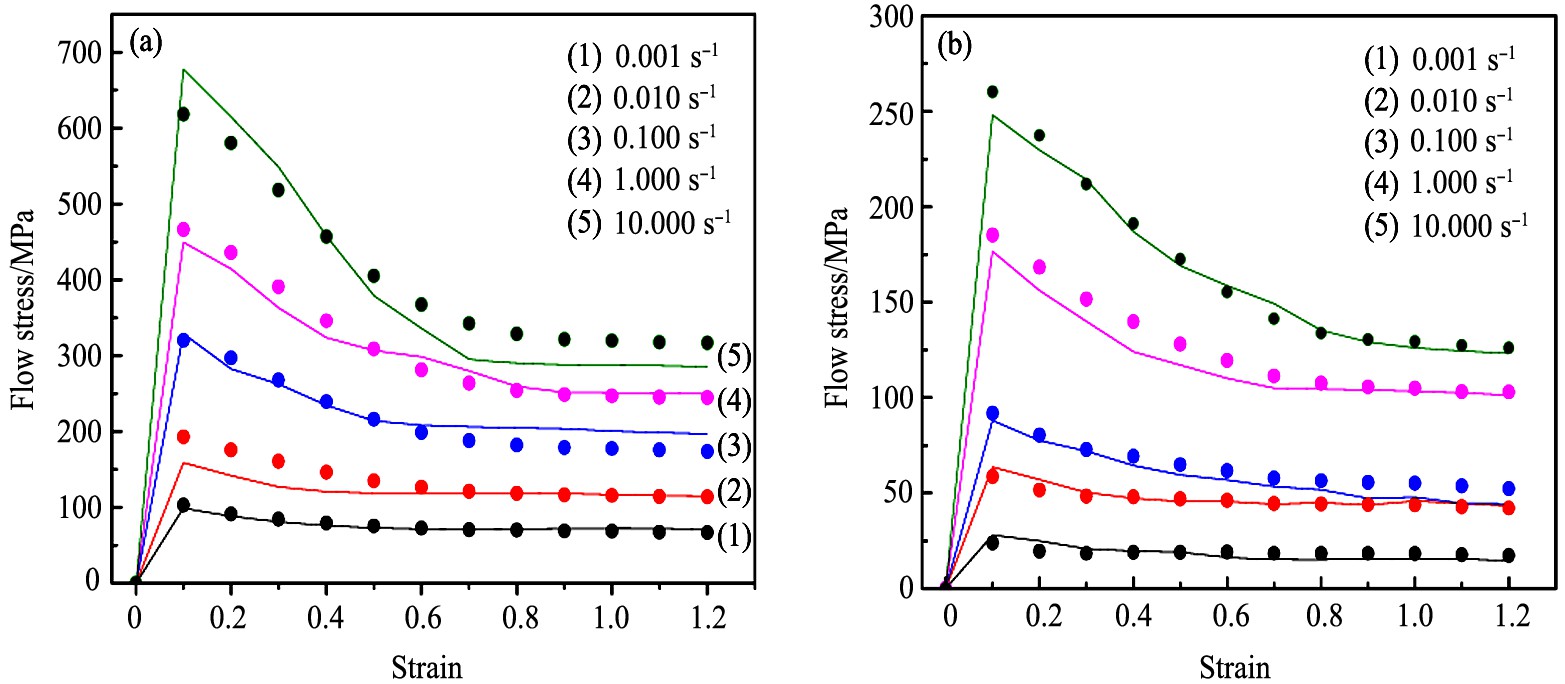
图7 不同变形条件下预测值与试验值的对比

Fig.7 Comparison between predicted value and test value under different deformation conditions

(a) T=990 ℃; (b) T=1100 ℃

图8 基于应变补偿本构模型的预测流动应力与实验值相关性

Fig.8 Correlation of prediction of flow stress and experimental value based on strain compensation constitutive model

4 结 论

1. Ti-22Al-24Nb-0.5Y合金经摩擦及温度修正的流变应力更能真实反映合金在高温变形过程中的动态响应。 经摩擦修正的流动应力小于实测值, 变形温度越高, 摩擦修正的流动应力越接近实测值; 低温高应变速率下, 温升引起的流动应力变化较为显著, 高于1050 ℃时, 温升引起的流动应力变化较小。

2. Ti-22Al-24Nb-0.5Y合金的流动行为对温度和应变速率的影响较为敏感。 随变形温度的降低, 流动应力逐渐升高, 随应变速率的升高, 合金流动应力越高; 当变形温度较高、 应变速率较低, 合金流动应力随应变量的增加变化不大。

3. 在传统Arrhenius本构模型的基础上考虑了应变对流动应力的影响, 采用4次多项式拟合应变与激活能Q和材料参数的函数关系, 建立的本构模型, 具有较高的预测精度, 其相关系数R达到0.9907, 平均相对误差E达到4.79%, 该模型预测的流动应力与实际流动应力吻合度较高, 符合热压缩过程中流动应力变化趋势。 该预测模型可作Ti-22Al-24Nb-0.5Y合金塑性成形过程中有限元模拟的本构关系。

参考文献

[1] Li S Q, Zhang J W, Cheng Y J, Liang X B.Current status on development of Ti₃Al and Ti₂AlNb intermetallic structural materials [J].Rare Metal Materials and Engineering, 2005, 34 (s1) :104. (李世琼, 张建伟, 程云君, 梁晓波.Ti₃Al和Ti₂AlNb基金属间化合物结构材料研发现状 [J].稀有金属材料与工程, 2005, 34 (s1) :104.)

[2] Chen Y Y, Kong F T.Research on TiAl based alloys materials and precision forming [J].Acta Metallurgica Sinica, 2002, 38 (11) :1141. (陈玉勇, 孔凡涛.TiAl基合金新材料研究及精密成形 [J].金属学报, 2002, 38 (11) :1141.)

[3] Si Y F, Meng L H, Chen Y Y.Research development of Ti₂AlNb-based alloy [J].Aerospace Materials and Technology, 2006, 36 (3) :10. (司玉锋, 孟丽华, 陈玉勇.Ti₂AlNb基合金的研究进展 [J].宇航材料工艺, 2006, 36 (3) :10.)

[4] Feng A H, Shen J, Li B B.Recent advanced on Ti₂AlNb-based alloys [J].Journal of Materials and Metallurgy, 2011, 10 (1) :30. (冯艾寒, 沈军, 李渤渤.Ti₂AlNb基合金的研究进展 [J].材料与冶金学报, 2011, 10 (1) :30.)

[5] Emura S, Tsuzaki K, Tsuchiya K.Improvement of room temperature ductility for Mo and Fe modified Ti₂AlNb alloy [J].Materials Science and Engineering A, 2010, 528 (1) :355.

[6] Shagiev M R, Galeyev R M, Valiakhmetov O R, Safiullin R V.Improved mechanical properties of Ti₂AlNb-Based intermetallic alloys and composites [J].Advanced Materials Research, 2008, 59:105.

[7] Guo H P, Zeng Y S, Li Z Q.Research progress of superplasticity of intermetallic Ti₂AlNb orthorhombic alloys [J].Aeronautical Manufacturing Technology, 2009, (10) :64. (郭和平, 曾元松, 李志强.O相合金Ti₂AlNb的超塑性研究进展 [J].航空制造技术, 2009, (10) :64.)

[8] Germann L, Banerjee D, Guédou J Y, Strudel J L.Effect of composition on the mechanical properties of newly developed Ti₂AlNb-based titanium aluminide [J].Intermetallics, 2005, 13 (9) :920.

[9] Du Z, Wu S.A kinetic equation for damage during superplastic deformation [J].Journal of Materials Processing Technology, 1995, 52 (2) :270.

[10] Zhang C, Li X Q, L i D S, Jin C H, Xiao J J.Modelization and comparison of Norton-Hoff and Arrhenius constitutive laws to predict hot tensile behavior of Ti-6Al-4V alloy [J].Transactions of Nonferrous Metals Society of China, 2012, 22 (S2) :s457.

[11] Duan Y P, Huang Z J, Yu X L, Xing C, Sun Y F.Flow stress behavior and constitutive model of as-cast TB6 titanium alloy based on friction correction [J].Chinese Journal of Rare Metals, 2014, 38 (2) :202. (段园培, 黄仲佳, 余小鲁, 邢昌, 孙宇峰.基于摩擦修正的TB6合金流变应力行为研究及本构模型建立 [J].稀有金属, 2014, 38 (2) :202.)

[12] Wu Y, Yi N, Qiao H J, Guo H S, Zhao H L, Yao X N.High-temperature deformation constitutive relationship model considering strain compensation of Nb10Zr alloy [J].Rare Metal Materials and Engineering, 2013, 42 (10) :2117. (武宇, 宜楠, 乔慧娟, 郭海生, 赵鸿磊, 姚修楠.Nb10Zr合金高温变形应变补偿型本构关系模型 [J].稀有金属材料与工程, 2013, 42 (10) :2117.)

[13] Cai Z W, Chen F X, Guo J Q.Constitutive model for elevated temperature flow stress of AZ41M magnesium alloy considering the compensation of strain [J].Journal of Alloys and Compounds, 2015, 648:215. (蔡志伟, 陈拂晓, 郭俊卿.考虑应变补偿的AZ41M镁合金高温流动应力本构模型 [J].合金与化合物, 2015, 648:215.)

[14] Chen G, Chen W, Ma L, Guo A Z, Lü J, Zhang Z M, Zheng S Q.Strain-compensated Arrhenius-type constitutive model for flow behavior of Al-12Zn-2.4Mg-1.2Cu alloy [J].Rare Metal Materials and Engineering, 2015, 44 (9) :2120. (陈刚, 陈伟, 马力, 郭安振, 吕娟, 张治民, 郑顺奇.Al-12Zn-2.4Mg-1.2Cu合金流动行为的应变补偿Arrhenius型本构模型 [J].稀有金属材料与工程, 2015, 44 (9) :2120.)

[15] Wanjara P, Sarraga M C, Jahazi M, Monajati H.Hot working behavior of near-α alloy IMI834 [J].Materials Science and Engineering A, 2005, 396 (1-2) :50.

[16] Ebrahimi R, Najafizadeh A.A new method for evaluation of friction in bulk metal forming [J].Journal of Materials Processing Tech., 2004, 152 (2) :136.

[17] Luo J T, Chen Y M, Yin Z M, Zhang Y S, Zhang C X.Stress strain curve and constitutive model of TA15 titanium alloy in hot deformation [J].Rare Metal Materials and Engineering, 2017, (2) :399. (骆俊廷, 陈艺敏, 尹宗美, 张艳姝, 张春祥.TA15钛合金热变形应力应变曲线及本构模型 [J].稀有金属材料与工程, 2017, (2) :399.)

[18] Gholamzadeh A, Taheri A K.The prediction of hot flow behavior of Al-6%Mg alloy [J].Mechanics Research Communications, 2009, 36 (2) :252.

[19] Zener C, Hollomon J H.Effect of strain rate upon plastic flow of steel [J].Journal of Applied Physics, 1944, 15 (1) :22.

[20] Sellars C M, Mctegart W J.On the mechanism of hot deformation [J].Acta Metallurgica, 1966, 14 (9) :1136.