文章编号:1004-0609(2011)11-2751-06
铝合金方环件压缩变形规律及机理
李 峰1, 徐永超2, 李 超1, 刘晓晶1
(1. 哈尔滨理工大学 材料科学与工程学院,哈尔滨 150040;
2. 哈尔滨工业大学 材料科学与工程学院,哈尔滨 150001)
摘 要:
为了揭示锻件预制坯中方环件压缩变形的机理,采用有限元模拟及试验,对7075铝合金方环件压缩过程进行分析,研究工艺条件对方环件压缩变形流动行为的影响规律。结果表明:随着方环件高度的增大,压缩变形不均匀性明显增大,金属沿径向外流量显著增多,且压缩变形后金属变形行为的复杂程度也随之增大。通过工艺实验进行了验证,所得与模拟结果吻合较好,为复杂锻件预制坯工艺的制定提供了理论依据。
关键词:
中图分类号:TG316 文献标志码:A
Deformation rule and mechanism in compress process of aluminium alloy square ring
LI Feng1, XU Yong-chao2, LI Chao1, LIU Xiao-jing1
(1. College of Materials Science and Engineering, Harbin University of Science and Technology,Harbin 150040, China;
2. School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China)
Abstract: In order to reveal the mechanism of the square ring compression of the pre-forging billet. The numerical simulation and experiment were employed to analyze the compression of square ring with 7075 aluminium alloy. The effect of deformation condition on the metal flow behaviour of aluminium alloy during the square ring compression was analyzed. The results show that with increasing the height-diameter ratio, the uniformity of deformation increases markedly, the metal outside flow along the radial increases significantly, and the complex degree of metal flow behavior also increases evidently. The results agree well with one of the numerical simulation. This provides a theoretical reference for the investigation of pre-fabricated billet technology.
Key words: aluminium alloy; square ring; compression; numerical simulation
镦粗是塑性成形中最基本的加工工序之一,也是复杂锻件成形中预制坯过程所采用的主要加工方法,所以,深入研究其变形特征可对复杂锻件成形的工艺方案设计提供理论依据[1]。
圆柱和圆环镦粗的变形特征为压缩变形,许多学者对此展开了深入研究[2-5]。如在压缩变形过程中对圆柱施加特定的外部约束条件,进而可使圆柱压缩过程中金属的变形流动行为发生相应的改变[6]。对3种传统减小圆柱压缩变形时产生鼓形措施的对比研究结果表明:套环内压缩减小鼓形的效果最为明显,在很大程度上提高了试件变形的均匀性,这与实际生产是相吻合[7]。因试件形状及工具接触等条件的不同,圆环与圆柱压缩的差异显著[8-11]。HAMZAH和STAHLBERG[12]通过对圆环在平板间压缩变形过程的模拟研究表明,在摩擦因数和变形程度相同的条件下,随着高径比的增大,圆环外径呈外凸单鼓形,内径的变形特征则为3种[12];摩擦显著影响圆环压缩变形过程中分流面的位置分布,ROBINSON和ARMSTRONG[13]通过对圆环压缩变形过程的深入分析,揭示了使用不同润滑剂时受压圆环的形状变化规律,进而确定了不同润滑剂作用时所对应的摩擦因数;利用超声波可显著降低金属的变形抗力,通过对比可知,常温时随着方环件高度的减小,超声波作用下圆环内径的缩减量均显著大于传统圆环压缩变形的结果,即使与圆环热压缩相比,超声波作用下圆环的内径缩减量仍略高一些[14]。
综上可知,目前研究多限于圆柱及圆环等简单形状[15],对于特殊几何变形体压缩行为的研究则鲜见报道。针对以上不足,本文作者以方环件压缩过程为例,通过数值模拟研究了工艺条件对金属变形流动的影响,并进行验证分析。
1 实验
1.1 有限元模型建立
采用有限元软件DEFORMTM-3D对成形过程进行模拟。为了减少单元划分数量、提高计算速度和时间,仅取坯料的1/4作为模拟研究对象。利用四面体单元对坯料进行离散,在计算过程中随时根据网格畸变的情况进行重划,以保证计算的精度和收敛性。沿对称面的法向速度为零,有限元模型如图1所示。
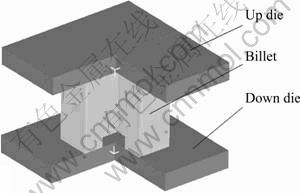
图1 有限元模型示意图(3/4)
Fig.1 Schematic diagram of finite element model(3/4)
模拟过程中不考虑模具的变形,材料属性为刚性体;坯料选用7075铝合金作为理想刚塑性模型材料。
1.2 模拟方案
研究用坯料为外边长24 mm及内边长分别为8和10 mm两种规格的方环件。压缩变形过程中影响方环件变形的因素很多,为了便于研究,模拟过程中,仅改变方形件的高度,分别取为10、15和20 mm,其它方环件的参数值均保持不变,以进行对比分析。压缩变形的成形速度为1 mm/s,温度为室温。
2 结果与分析
2.1 方环件的形状变化特征
图2所示为外边长为24 mm、内孔边长为10 mm的方环件在不同高度下压缩变形特征对比。
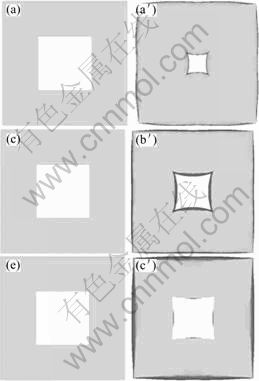
图2 不同高度方环件压缩变形特征对比(内边长10 mm)
Fig.2 Comparison of compression deformation of square rings with different heights (inner width 10 mm): (a), (a′) 10 mm; (b), (b′) 15 mm; (c), (c′) 20 mm; (a) 15 step; (a′) 35 step; (b) 15 step; (b′) 35 step; (c) 15 step; (a′) 35 step
从图2(a)和(a′)可以看出,方环件压缩变形后外侧呈外凸双鼓形,内侧为内凸单鼓形。随着压下量的增大,方环外侧双鼓变形趋势更为显著,内侧孔径则进一步缩小。由此可见,压缩过程中金属沿径向内流的变形趋势更为显著。高度增大为15 mm时(见图2(b)和(b′)),随着压下量增大,方环件外侧及内孔的变形特征与前者类似,但内孔径向缩减率显著降低,由此可知,金属沿径向内流量明显减小;当高度增大到20 mm时,随着压下量的增大,方环外边呈外凸单鼓变形趋势,如图2(c)和(c′))所示,内孔径缩减率则进一步降低,而沿径向外流量则显著地增大。
由此可知,当方坯件外边长为24 mm、内孔边长为10 mm时,随着坯料高度的增加,方环件压缩过程中外侧变形特征由外凸双鼓形转变为外凸单鼓形,金属沿径向向外侧变形量显著增大,内孔径向缩减率显著降低。
外边长为24 mm、内孔边长为8 mm的方环件,不同坯料高度下方环件的压缩变形特征对比如图3所示。

图3 不同高度压缩变形特征的对比(内边长8 mm)
Fig.3 Comparison of compression deformation of square rings with different heights (inner width 8 mm): (a) 15 step, 10 mm; (a′) 35 step, 10 mm; (b) 15 step, 15 mm; (b′) 35 step, 15 mm; (c) 15 step, 20 mm; (c′) 35 step, 20 mm
由图3(a)和(a′)可以看出,方环件压缩后内外侧均呈外凸单鼓形变形。随着压下量的继续增大,方环外边的鼓形变形更加显著,而内孔孔径显著缩小,因此可知,压缩过程中变形体沿径向的变形分布相对较均匀。当高度为15 mm时,如图3(b)和(b′)所示,随着压下量的增大,方环件外侧外凸单鼓形变形趋势增大,内孔依然呈单鼓形,但变形量较小。当压下量增大时,方环件外侧外凸单鼓形趋势更显著,但内孔径缩减率相对降低,可知此时金属沿径向内流量相对减小;当高度增大至20 mm时,如图3(c)和(c′)所示,方环件外侧外凸单鼓形变形趋势更加显著,内孔缩减率则进一步降低,金属沿径向的变形行为相对集中在外边区域。研究结果表明,当坯料外边长为24 mm,内孔边长为8 mm时,随着坯料高度的增加,压缩过程中方环外边的外凸单鼓变形趋势更加明显,同时金属沿径向向外侧的变形量明显增大,金属沿径向的内孔变形量逐渐减少。
2.2 等效应力分析
图4所示为外边长为24 mm、内孔边长为10 mm的方环件在不同压缩过程中等效应力分布对比。
由图4(a)可以看出,压下量为10步时,坯料中等效应力数值最大处分布在方环外侧上下边棱及内孔中部,该处开始发生塑性变形。而端面处靠近内孔附近区域等效应力数值较小,相对前者发生塑性变形相对滞后;随着压下量的增大,变形体中最大等效应力分布在方环外边、内孔的中部及上下端面靠近内孔处,等效应力最小值则分布在方环外边的上下棱。由此可知,随着压下量的增大,外侧由两端向中心转移,内侧则主要集中于中间部位并逐渐增大;当坯料高度为15 mm时,如图4(b)所示,压下量为15步时,坯料中最大等效应力分布在方环外侧的上下棱和内孔中部,等效应力最小值则分布在上下端面靠近内孔处;当压下量增大到35步时,坯料中的最大等效应力分布在方环外边的中部以及上下端面除内孔附近的大部分区域,等效应最小值则分布在方环外边的上下棱。经对比可知,随着压下量的增大,外边由两端向中部区域转移并在整个外边呈现均匀的分布,上下端面区域的金属变形趋势也明显,而内边中部区域变形趋势相对减弱;当坯料高度增大至20 mm,如图4(c)所示,压下量为15步,等效应力分布趋势与前者大致相同,但最大值降低至594 MPa,等效应力数值较小区域分布与前者分布相同,但最小值降低至329 MPa。当压下量增大到35步时,坯料中最大等效应力分布在除棱边外的绝大部分区域,因此可知,此时绝大部分区域都发生塑性变形,而外侧棱边处和内侧中部区域变形相对困难。

图4 不同压缩过程中不同坯料高度时等效应力分布对比(内边长10 mm)
Fig.4 Comparison of equivalent stress distribution of square rings (inner width 10 mm): (a), (a′) 10 mm; (b), (b′) 15 mm; (c), (c′) 20 mm
外边长为24 mm,内孔边长为8 mm的方环件,在不同压缩过程中等效应力分布对比如图5所示。
从图5(a)和(a′)可以看出,坯料高度为10 mm时,压下量为10步,等效应力较大值仍分布于外侧棱边和内孔中部,等效应力最小值分布则于端面上靠近内孔处;当压下量增大到25步,坯料中等效应力较大值分布于外侧和内孔中部及端面内孔处,该区发生了塑性变形,等效应力较小值分布于方环件外侧棱边处,可知等效应力分布变化趋势如下:随着压下量增大,外侧由两端向中心转移,内边则主要集中于中间部分并逐渐增大。当坯料高度为15 mm,如图5(b)和(b′)所示,压下量为15步,变形体中等效应力分布趋势与前者相似,仅数值略有升高。且由对比可知等效应力分布变化趋势如下:随着压下量增大,外侧由两端向中部区域转移,端面区金属的变形趋势显著,而内侧中部区的变形相对趋势减弱。高度增大至20 mm,如图5(c) 和(c′)所示。变形体中等效应力分布趋势如下:外侧由两端逐渐扩展为整个区域,端部发生塑性变形区明显扩大,而内侧中部塑性变形区显著缩小。

图5 不同压缩过程中不同压坯高度时等效应力分布对比(内边长8 mm)
Fig.5 Comparison of Equivalent stress distribution (inner width 8 mm): (a), (a′) 10 mm; (b), (b′) 15 mm; (c), (c′) 20 mm
2.3 金属流动行为
外边长为24 mm,内孔边长为10 mm的方环件,压缩变形过程中速度矢量场分布对比如图6所示。
从图6(a)可以看出,压下量为10步,方环件外侧由上至下速度值逐渐减小,其端部金属的流速最快,而方环件内侧速度矢量分布与外边相似,但同一平面上内侧流速值要显著低于外侧。压下量增加至25步(见图6(a′)),坯料金属流动最快的区域集中在外边,且整个外侧速度场的分布变得均匀,而与压缩方向夹角显著增大,且随压缩量增加,金属沿径向的流速增大;图6(b)、(b′)所示分别为变形体高度15 mm、20 mm时的速度矢量分布对比。当压下量较小时(见图6(b)和(c))中变形初期,其速度矢量的分布规律大致与前者相似,且在同一平面上内外侧流速也变得相对均匀;但随着压下量继续增大(见图6(c)和(c′)),其速度矢量的分布与高度10 mm时有一定差异,但变形体外侧速度值仍为由上到下递减的趋势分布。
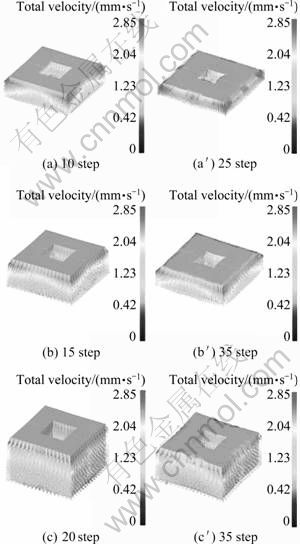
图6 速度矢量分布对比(内边长10 mm)
Fig.6 Comparison of velocity field distribution (inner width 10 mm): (a), (a′) 10 mm; (b), (b′) 15 mm; (c), (c′) 20 mm
图7所示为外边长为24 mm,内孔边长为10 mm的方环件,压缩变形过程中速度矢量场分布对比。
如图7(a)所示,当压下量为10步,金属流动速度最快的区域为方环外边上部,方环件外侧速度值仍为由上到下递减,方环件内侧速度分布与外侧相似;压下量增大至25步(见图7(a′)),坯料金属流动最快的区域集中在外边,且外侧速度矢量分布变得相对均匀,与压缩方向夹角则显著变大,但同一平面内侧值仍小于外侧。图7(b)和(c)所示分别为方环件高度为15和20 mm时速度场分布对比。当压下量较小时,其速度矢量的分布规律大致与高度10 mm时相同,当压下量继续增大,高度15 mm的变形体外侧速度矢量值仍为由上到下递减规律分布,上速度场呈相对均匀分布,但速度矢量数值较小,即金属的流动趋势相对缓慢。

图7 速度矢量分布对比(内边长8 mm)
Fig.7 Comparison of velocity field distribution (inner width 8 mm): (a), (a′) 10 mm; (b), (b′) 15 mm; (c), (c′) 20 mm
3 实验验证
该实验是在1 000 kN油压万能材料试验机上进行的,通过控制台控制压缩的位移、速度等。采用百分表观测滑块行程即方环件的相对压缩量,其它条件均与模拟相同。
图8所示为外边长24 mm,内边长分别为8、10 mm的方环件在不同压下量的实验结果对比。
经对比可知,随着压下量的增加,内外侧压缩变形趋势相对均匀,端面形状变化并不明显,金属的流动方向多与压缩方向一致;外边长24 mm,内边长8 mm的方环件,随着压下量的增加,内侧呈明显地外凸单鼓形变形,外侧也呈现出较为显著地外凸变形,相对于内边长10 mm的方环件,端面形状的变化较显著,即金属沿径向的变形量相对增大。

图8 压缩结果对比
Fig.8 Comparison of compression results: (a), (a′) Blank; (b), (b′) After deformation; (a), (b) Outer width 24 mm; (a′), (b′) Outer width 24 mm, inner width 10 mm
4 结论
1) 方环件压缩变形过程中,随着高径比增加,金属沿径向内流量逐渐减小,而向外流动的金属量显著增大。
2) 当变形程度相同时,方环件压缩变形过程中金属流动复杂程度随坯料高度的增加而加大。
3) 当方环的内边长逐渐减小,端面面积增大,即高径比减小,金属的轴向上的变形量逐渐减少,径向上的变形量逐渐增加,即金属沿轴向越难以压缩,坯料上下端面的形状变化越发明显。
REFERENCES
[1] 李 峰. 盘类件模锻过程金属变形模式及流动规律研究[D]. 哈尔滨工业大学, 2007.
LI Feng. Deformation modes and flow behaviour of metal in die forging process of disk components[D]. Harbin: Harbin University of Science and Technology, 2007.
[2] MUNGI M P, RASANE S D, DIXIT P M. Residual stresses in cold axisymmetric forging[J]. J Mater Process Technol, 2003, 142(1): 256-266.
[3] LIU Z B, NIE M S, WANG L D. A new theory for upsetting a cylinder between flat platens[J]. Chinese Journal of Mechanical Engineering, 1992, 5(4): 297-303.
[4] 刘助柏, 倪利勇, 梁 晨, 刘国晖, 邓冬梅. 普通平板镦粗高圆柱体的拉应力理论的模拟[J]. 中国机械工程, 2005, 16(1): 74-77.
LIU Zhu-bai, NI Li-yong, LIANG Chen, LIU Guo-hui, DENG Dong-mei. Simulation of tensile stress theory of conventional upsetting between flat plates for high cylindrical forgings[J]. China Mechanical Engineering, 2005, 16(1): 74-77.
[5] 詹艳然, 张中元, 王仲仁. 对圆柱体镦粗过程中塑性变形发生和发展的探讨[J]. 塑性工程学报, 1999, 6(2): 82-85.
ZHAN Yan-ran, ZHANG Zhong-yuan, WANG Zhong-ren. Study of production and development of plastic deformation in the upsetting process of a cylinder[J]. Journal of Plasticity Engineering, 1999, 6(2): 82-85.
[6] SCHLEMMER K L, OSMAN F H. Differential heating forming of solid and bi-metallic hollow parts[J]. J Mater Process Technol, 2005, 162/163: 564-569.
[7] 孙前江, 王高潮. 减小镦粗鼓形的措施及有限元模拟分析[J].南昌航空工业学院学报: 自然科学版, 2004, 18(1): 34-38.
SUN Qian-jiang, WANG Gao-chao. Measures of decreasing drum shape and simulation analysis of FEM in the upsetting process[J]. Journal of Nanchang Institute of Aeronautical Technology: Natural Science, 2004, 18(1): 34-38.
[8] MEINERS F, R?HR S, SCHMIDT-JURGENSEN R. Extension of forming limits in forging of less ductile light weight metals by means of superimposed hydrostatic pressure[C]//Advanced Technology of Plasticity, 2002: 37-42.
[9] KUGLER D, MOON T J. A technique for compression testing of composite rings[J]. Composites A, 2002, 33: 507-514.
[10] YEH Wei-ching, WU Ming-chang. A variational upper-bound method for analysis of upset forging of rings[J]. J Mater Process Technol, 2005, 170(1/2): 392-402.
[11] LIU Gang, WANG Li-liang, YUAN Shi-jian, WANG Zhong-ren. Compressive formability of 7075 aluminum alloy rings under hydrostatic pressure[J]. Transactions of Nonferrous Metals Society of China, 2006, 16(4): 1103-1109.
[12] HAMZAH S, STAHLBERG U. A study of pore closure in the manufacturing of heavy rings[J]. J Mater Process Technol, 1998, 84(1/3): 25-37.
[13] ROBINSON T, OU H, ARMSTRONG C G. Study on ring compression test using physical modeling and FE simulation[J]. J Mater Process Technol, 2004, 153/154: 54-59.
[14] HUNG Jung-chung, TSAI Yu-chung, HUNG Ching-hua. Frictional effect of ultrasonic-vibration on upsetting[J]. Ultrasonics, 2007, 46(3): 277-284.
[15] HASAN S, JAHAN R. On the measurement of friction coefficient utilizing the ring compression test[J]. Tribology International, 1999, 32(6): 327-335.
(编辑 龙怀中)
基金项目:黑龙江省博士后科研启动基金资助项目(LBH-Q10065);哈尔滨市青年科技创新人才基金资助项目(2010RFQXG021)
收稿日期:2010-02-25;修订日期:2011-07-11
通信作者:李 峰,副教授,博士;电话:0451-86392501;E-mail: hitlif@126.com
摘 要:为了揭示锻件预制坯中方环件压缩变形的机理,采用有限元模拟及试验,对7075铝合金方环件压缩过程进行分析,研究工艺条件对方环件压缩变形流动行为的影响规律。结果表明:随着方环件高度的增大,压缩变形不均匀性明显增大,金属沿径向外流量显著增多,且压缩变形后金属变形行为的复杂程度也随之增大。通过工艺实验进行了验证,所得与模拟结果吻合较好,为复杂锻件预制坯工艺的制定提供了理论依据。


