J. Cent. South Univ. Technol. (2011) 18: 319-322
DOI: 10.1007/s11771-011-0698-2
CC-CV charge protocol based on spherical diffusion model
LI Lian-xing(李连兴)1, TANG Xin-cun(唐新村)1, 2, QU Yi(瞿毅)1, LIU Hong-tao(刘洪涛)1
1. School of Chemistry and Chemical Engineering, Central South University, Changsha 410083, China;
2. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract:
A new insight into the constant current–constant voltage (CC–CV) charge protocol based on the spherical diffusion model was presented. From the model, the CV-charge process compensates, to a large extent, the capacity loss in the CC process, and the capacity loss increases with increasing the charging rate and decreases with increasing the lithium-ion diffusion coefficient and using a smaller τ value (smaller particle-size and larger diffusion coefficient) and a lower charge rate will be helpful to decreasing the capacity loss. The results show that the CC and the CV charging processes, in some way, are complementary and the capacity loss during the CC charging process due to the large electrochemical polarization can be effectively compensated from the CV charging process.
Key words:
lithium-ion battery; charge protocol; constant current-constant voltage mode; capacity loss；
1 Introduction
The lithium-ion secondary batteries have been extensively used in many portable electronic devices such as laptop computers, camcorders and cellular phones. The reaction process in the lithium-ion batteries can be briefly described as the lithium-ion transfer between the positive and negative electrodes through an ionically conducting phase [1]. In fact, the ion transfer at the interface between the positive (and negative) electrode and electrolyte is the most fundamental reaction during the charging and discharging processes in the lithium-ion batteries. The intercalation (or deintercalation) of lithium ions in both the positive and the negative electrode matrices determines the battery charging and discharging rate to a large extent [2-6]. Since the intercalation/deintercalation process is controlled by the lithium-ion diffusion, it is necessary to apply a low charging rate in case of serious polarization. So far, a substantial amount of work has been devoted to the study of the charging technology [7-12], among which the constant current–constant voltage (CC–CV) mode (i.e. low rate constant current charging to a predetermined cut-off potential followed by the float charging at the cut-off potential until the current drops to a very low preset value) is mostly employed and seems to be more effective in practice.
In this work, a theoretical model associated with the CC-CV charging protocol is proposed, and a plausible explanation for this generally used charging technique is provided. It is highlighted that the kinetics in the charging process plays the most key role.
2 Theoretical modeling
The porous electrode filled with electrolyte solution was modeled in the previous work [13]. Because the diffusion coefficient of Li+ in the porous electrode (ca. 10-12 cm2/s) is much smaller than that in the electrolyte solution (ca. 10-5cm2/s), the solution-phase diffusion resistance could be neglected rationally [14].
According to the Fick’s Second Law, the spherical diffusion equation and initial boundary conditions can be expressed as
(1)
(2)
(3)
(4)
where c(r, t) is the concentration distribution of Li+ in the porous material, r and t are the corresponding radius and time, R is the radius of particles, D is the intercalation diffusion coefficient, c* is the initial Li+ concentration, I represents the charge/discharge current of single particle, n is the ion charge (for Li+, n=1), F is Faraday constant, and A is the surface area of particle.
From the above Eqs.(1)-(4), the concentration distributions, c(r, t) and c(R, t), can be solved as [1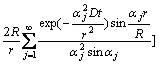5]
(5)
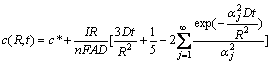
(t≤R2/10D) (6)
where c(R, t) is the concentration of Li+ in the porous electrode, and αj is the positive roots of equation: tan α=α.
The polarization capacity loss caused by the Li+ diffusion in the insertion-host materials during the constant-current charge process is analyzed as follows. According to the Faraday’s law, the amount of Li+ extracted from the porous host in the CC charge process can be expressed as
(7)
By assuming that tcc is the CC charging time, Eq.(7) is changed into
(8)
Obviously, It item is just the theoretical charge capacity in the CC process (Ccc), that is to say, if 1C rate is applied to charge the battery, it should take 1 h to charge the battery to the nominal capacity. However, in most real cases, the batteries would automatically end the CC charge process (less than 1 h) before the arrival of nominal capacity.
In order to further evaluate and pinpoint the capacity loss in the CC process, a charging mode is designed as: first CC-charge to a preset voltage, and then CV-charge to nearly zero current (0.02C). One can see From Eq.(4) that the flux of Li+ in the porous electrode host is also approximately equal to zero. Thus,
(9)
Supposing that the Li+ concentration distribution in the porous host is uniform and equal to the surface concentration c(R,t), the total amount of Li+ deintercalated during total charge process can be expressed as
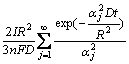(10)
Let z=r/R and τ=R2/D, and define S(t, τ) as potentio- over-compensation-factor:
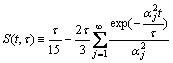(11)
Thus, Eq.(10) can be written as
(12)
(13)
where 
item represents the excessive amount
of Li+ deintercalated during the overall charge process compared with the theoretical amount It/nF in the CC process. Eq.(12) shows that the CV-charge process compensates the capacity loss in the CC process to a large extent. This also indicates that the CV-charge process plays an important role in improving the charge capacity of batteries.
3 Experimental
The BYD commercial quadrate lithium-ion batteries (LP063450AR Model) with a nominal capacity of 950 mA?h were used for tests. The constant current–constant voltage (CC–CV) charging and CC discharging protocols were adopted. (0.2-2)C of currents was used to charge the batteries to the cut-off voltage of 4.2 V. Then, the batteries were further charged at 4.2 V till the current dropped to 20 mA. After finishing charge process, the batteries were discharged with (0.2-2)C of currents to the cutoff voltage of 3.0 V. By Using this CC-CV charging protocol, the batteries achieved basically the nominal capacity. All tests were carried out on a LAND CT2001A batteries test instrument at room temperature.
4 Results and discussion
As presented in Eq.(13), the charge capacity loss in the CC charge step is associated with the charge current, charge time, radius of particles, and lithium-ion diffusion coefficient. It can be seen from Fig.1 that the charge capacity loss increases with increasing the charge current and t (t=R2/D). In the previous work [16], the t value of 8 500 around was got. Here, t=8 500 (7 500, 10 000) was chosen to simulate the charge capacity loss (Fig.1). For the convenient comparison, (0.2-2)C of currents was used in experiments to charge the batteries during the CC charging process. It is obvious that using a smaller t (smaller particle size and larger diffusion coefficient) and a lower charge rate will be helpful to decreasing the capacity loss. Also, it can be observed from Fig.2(b) that the simulated capacity loss during the CC charging process is just compensated from the followed CV charging process.
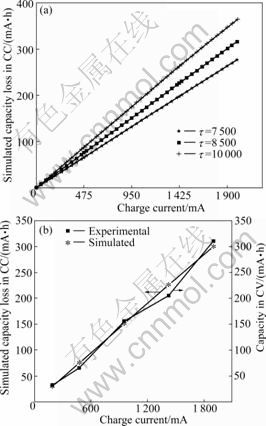
Fig.1 Simulated capacity losses in CC charge step at different charge currents (a) and comparison of charge capacity in CV charge step and simulated capacity loss in CC charge step at (0.2-2)C charge rates (b)
The variation of voltage/current of batteries with time and capacity at different charge rates are shown in Fig.2. The BYD batteries were charged at a constant current (0.2-2)C to a predetermined cut-off voltage (4.2 V) followed by the float charging at 4.2 V until the current dropped to a very low preset value (20 mA). During the CC charging, the cell voltage slowly climbs and the charge capacity of the battery increases linearly. Taking charging the battery at 1C for example, when the voltage climbs to the upper limit (4.2 V), the charge capacity reaches 83.3% of the total capacity. The remained 16.7% capacity could be attained through reducing the charge current during the CV charging process. The total charging time and its distribution between the CC and CV processes are determined by the charging current. Generally, a higher time ratio of CC to CV favors a longer battery life, but it requires a longer charging time [17]. As shown in Fig.2(c), the charge time increases visibly with increasing the charging current.
As shown in Fig.3, the charge capacity/time for batteries during the constant current (CC) charge and Variation of voltage and current of batteries with capacity; (c) Relationship between charge capacity and time
constant voltage (CV) charge vary with the charge current. The CC charge capacity decreases with increasing the charge current (e.g. from 899.9 mA?h at 0.2C to 623.3 mA?h at 2C, and about 69.2% of it at 0.2C), whereas the CC charge time also decreases very quickly (e.g. from 284.2 min at 0.2C to 19.7 min at 2C, and about 0.07% of it at 0.2C). On the contrary, the CV charge capacity increases with increasing the charge current (e.g. from 31.9 mA?h at 0.2C to 310.3 mA?h at 2C, and about 10.3% of it at 0.2C), whereas the CV charge time increases remarkably (from 27.9 min at 0.2C to 51.4 min at 2C, and about 184.2% of it at 0.2C). Interestingly, it is noted that the CC and the CV charging processes, in some way, are complementary and the capacity loss during the CC charging process due to the large electrochemical polarization can be effectively compensated from the CV charging process.
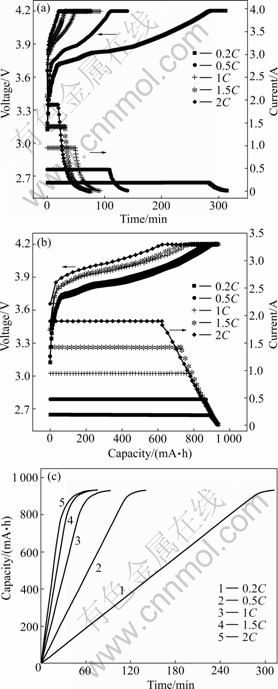
Fig.2 Typical CC-CV charging profiles of BYD LP063450AR batteries: (a) Variation of voltage and current of batteries with time; (b)
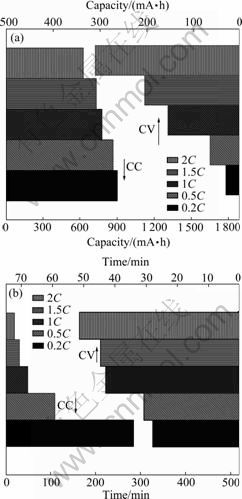
Fig.3 Variations of charge capacity (a) and time (b) for BYD LP063450AR batteries during constant current (CC) charge and constant voltage (CV) charge with different charge currents
5 Conclusions
1) The constant current–constant voltage (CC–CV) charging protocol and the capacity loss in the CC step are successfully simulated based on the spherical diffusion mode.
2) The capacity loss represented in the model in the CC step is confirmed during the CC-CV mode of charging in the charging test. The results show that the capacity loss in the CC step results from the electrochemical polarization due to the larger charge currents and lower lithium-ion diffusion coefficient and can be mostly compensated in the CV charge step.
3) From the model, it is obviously observed that the capacity loss increases with increasing the charging current and the radius of particles, and decreases with increasing the lithium-ion diffusion coefficient. Thus, the smaller particle-size, larger diffusion coefficient and lower charge rates are beneficial to decreasing the capacity loss in the charging process.
References
[1] ABE T, SAGANE F, OHTSUKA M, IRIYAMA Y, OGUMI Z. Lithium-ion transfer at the interface between lithium-ion conductive ceramic electrolyte and liquid electrolyte—A key to enhancing the rate capability of lithium-ion batteries
[2] ARORA P, WHITE R E, DOYLE M. Capacity fade mechanisms and side reactions in lithium-ion batteries
[3] RAMADASS P, DURAIRAJAN A, HARAN B, WHITE R E, POPOV B N. Studies on capacity fade of spinel-based Li-ion batteries [J]. J Electrochem Soc, 2002, 149(1): A54-A60.
[4] AURBACH D, MARKOVSKY B, WEISSMAN I, LEVI E, EIN-ELI Y. On the correlation between surface chemistry and performance of graphite negative electrodes for Li ion batteries
[5] DOYLE M, NEWMAN J, GOZDZ A S, SCHMUTZ C N, TARACSON J M. Comparison of modeling predictions with experimental data from plastic lithium ion cells
[6] BROUSSLEY M, BIENSAN P, SIMON B. Lithium insertion into host materials: The key to success for Li ion batteries [J]. Electrochim Acta, 1999, 45(1/2): 3-22.
[7] NOTTEN P H L, OP HETVELD J H G, VAN BEEK J R G. Boostcharging Li-ion batteries: A challenging new charging concept
[8] LIN P C, LIU Y H, LIU YH, CHEN J K, CHEN C H. A fully digital rapid charger for electric scooters [J]. Proceedings of 18th Symposium on Electrical Vehicles, Session D7A, 2001: 1-13.
[9] LIU Y H, TENG J H, LIN Y C. Search for an optimal rapid charging pattern for lithium-ion batteries using ant colony system algorithm [J]. IEEE Trans Ind Electron, 2005, 52(5): 1328-1336.
[10] CHUNG S K, ANDRIIKO A A, MON’KO A P, LEE S H. On charge conditions for Li-ion and other secondary lithium batteries with solid intercalation electrodes
[11] SIKHA G, RAMADASS P, HARAN B S, WHITE R E, POPOV B N. Comparison of the capacity fade of Sony US 18650 cells charged with different protocols
[12] LI J, MURPHY E, WINNICK J, KOHL P A. The effects of pulse charging on cycling characteristics of commercial lithium-ion batteries
[13] TANG X C, PAN C Y, HE L P, LI L Q, CHEN Z Z. A novel technique based on the ratio of potentio-charge capacity to galvano- charge capacity (RPG) for determination of the diffusion coefficient of intercalary species within insertion-host materials: Theories and experiments [J]. Electrochimica Acta, 2004, 49(19): 3113-3119.
[14] VERBRUGGE M W, KOCH B J. Electrochemistry of intercalation materials: Charge-transfer reaction and intercalate diffusion in porous electrodes
[15] TANG Z Y, XUE J J, LI J G, WANG Z L. Discharge process of insertion electrodes controlled by lithium ion diffusion in solid materials [J]. Acta Phys-Chim Sin, 2001, 17(6): 526-530.
[16] JIN L, TANG X C, PAN C Y, JIANG C K. Variation of solid diffusion coefficient for lithium ions in LiCoO2 with charge- discharge cycles
[17] ZHANG S S, XU K, JOW T R. Study of the charging process of a LiCoO2-based Li-ion battery
(Edited by YANG Bing)
Foundation item: Projects(20676152, 20876178) supported by the National Natural Science Foundation of China
Received date: 2010-01-31; Accepted date: 2010-06-02
Corresponding author: TANG Xin-cun, Professor, PhD; Tel: +86-731-88836961; Fax: +86-731-88879616; E-mail: tangxincun@163.com
