- Abstract:
- 1 Introduction▲
- 2 Governing equation...▲
- 3 Numerical results ...▲
- 4 Conclusions▲
- References
- Figure
- Fig. 1 A floating pile in a saturated viscoelastic soil layer overlaying bedrock
- Fig. 2 Comparison of results of present work and Ref. [25]:
- Fig. 3 Comparison of results of present work and WU [26]:
- Fig. 4 Comparison of results of present work and other cases [6, 25]:
- Fig. 5 Effect of relative depth of pile–bedrock on dynamic impedance:
- Fig. 6 Effect of liquid-to-solid coupled coefficient on dynamic impedance:
- Fig. 7 Effect of length-to-radius ratio of pile on dynamic impedance:
- Fig. 8 Effect of relative rigidity of pile–soil on dynamic impedance:
- Fig. 9 Effect of viscous damping coefficient of soil on dynamic impedance:
J. Cent. South Univ. (2016) 23: 220-232
DOI: 10.1007/s11771-016-3065-5
Vertical vibration of a floating pile in a saturated viscoelastic soil layer overlaying bedrock
CUI Chun-yi(崔春义)1, 2, ZHANG Shi-ping(张石平)1, YANG Gang(杨刚)1, LI Xiao-fei(李晓飞)1
1. Institute of Road and Bridge Engineering, Dalian Maritime University, Dalian 116026, China;
2. School of Civil Engineering, Beijing University of Technology, Beijing 100022, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract:
An axisymmetrical analytical solution is developed to investigate the vertical time-harmonic vibration of a floating pile in a saturated viscoelastic soil layer overlaying bedrock. The soil is described by porous medium model established by Boer, while the pile is described by a beam vibration theory. By using separation theory of differential operator and variables to solve the dynamic governing equations for the soil, the fundamental solutions for the soil reactions on side and bottom of the pile are obtained. The dynamic impedance of the pile head is then derived by solving the vibration equation for the pile according to the compatibility condition between the pile and the soil. The proposed model is validated by comparing special cases of our model with the existing results. Numerical examples are presented to analyze the vibration characteristics of the pile.
Key words:
1 Introduction
The dynamic interaction between saturated soil and pile is the key of studying the vibration characteristics of single pile, group piles and pile–soil-structure system, and important for further comprehension of mechanism of pile–soil system and guidelines of quakeproof and impact-absorbing design and nondestructive testing of piles in saturated soil. The problem was given increasing importance from scholars in recent years. YU et al [1] presented an analytical method for the elastic analysis of vertically loaded single pile in multilayered saturated soil based on plane strain assumption. WANG et al [2–3] developed comprehensive analytical solutions to investigate the harmonic torsional vibration of an end bearing pile embedded in a homogeneous poroelastic medium and transversely isotropic saturated soil, respectively. HU et al [4] investigated the influence of initial strain state on the dynamic response of an end bearing pile embedded in isotropic saturated soil through the linearized theory of small elastic perturbation superposed on largely stressed bodies. LIU et al [5] developed an analytical solution to investigate the vertical time-harmonic response of a pipe pile embedded in a viscoelastic saturated soil layer. These studies were for end-bearing pile, and no consideration of the dynamic interaction between pile and the soil under pile bottom was taken.
Except for these cases on end-bearing pile, dynamic responses of floating pile in saturated soil were also studied extensively. ZENG and RAJAPAKSE [6] considered the time-harmonic response of an elastic pile partially embedded in a homogeneous poroelastic medium and subjected to a vertical load by establishing the second kind of Fredholm’s integral equation. JIN et al [7] studied the time-harmonic response of a pile in a poroelastic half space under lateral loadings by establishing Green’s functions for distributed lateral force field acting inside a poroelastic half space. LU et al [8–9] investigated the frequency domain dynamic responses of a pile embedded in a porous medium subjected to SH seismic waves, and layered poroelastic half-space to an axial harmonic load, respectively, by using the Hankel’s integral transformation, Muki and Sternberg’s fictitious pile methodology, and transmission and reflection matrices. CAI et al [10] studied the response of a cylindrical elastic pile embedded in a homogeneous poroelastic medium and subjected to torsional loading based on Muki’s fictitious pile model. WANG et al [11] investigated the axisymmetrical dynamic response of single pile vertically embedded in the saturated half space and subjected to harmonic torsional loadings by means of integral transform and Muki’s methods. ZHOU et al [12] analyzed the dynamic response of a pile embedded in a saturated half-space subjected to transient vertical loading by the fictitious pile model. XU et al [13] investigated the isolation of the vibration due to harmonic Rayleigh waves using pile rows embedded in a saturated poroelastic half-space based on the potential function method and Muki’s method. CAI et al [14] studied the transient dynamic response of an elastic pile in viscoelastic saturated soil by using Laplace transform and thin layers method. CHEN et al [15] studied the transient dynamic response of a pile embedded in transversely isotropic saturated soil and subjected to transient torsional loading by using Laplace transform and thin layers method. LI et al [16] established a dynamic model of a friction pile embedded in saturated soil on the basis of interface model with a frequent-dependent damping between the pile and soil, with the use of potential functions. But, their studies were only suitable to the half space without bedrock, and unable to consider the effect of the bedrock on the vibration characteristics of pile–soil system. Actually, in many cases, the saturated soil may rest on rigid bedrock and the study on vibration characteristic of a floating pile in the soil is important in the guidance for engineering application. To the author’s best knowledge, less work has been done on the vertical vibration of a floating pile in the saturated soil layer overlaying bedrock. In this work, the vertical vibration of a floating pile in a saturated viscoelastic soil layer overlaying bedrock will be studied by employing analytical method.
It should be noted that the above-mentioned studies employed Biot’s theory to describe the mechanical behaviors of saturated soil. Although the motion equations proposed by Biot have been successfully applied in many engineering domains, as pointed out by EDELMAN and WILMANSKI [17] and BOER [18], they are not developed from the fundamental axioms and principles of mechanics and thermodynamics. Thus, the subsequent conclusions are unsatisfactory. By contrast, the porous medium model established by BOER and LIU [18–19] is not only able to meet the requirements, but also has many advantages. For example, it coincides with the axioms of continuum mechanics, and the huge formalism of the mixture theory due to the averaging procedure can be abandoned. Furthermore, some microscopic properties of saturated porous medium can be presented in macroscopic quantities directly. Especially, its validity has been verified in existing studies [18–23].
In light of these, the purpose of this work is to present the first attempt in studying the vertical vibration of a floating pile embedded in saturated viscoelastic soil layer overlaying bedrock. The soil is described by mentioned Boer’s porous medium model, while the pile embedded in the soil is treated as a beam and described by a beam vibration theory. By using separation theory of differential operator and variables to solve the dynamic governing equations for the soil, the fundamental solutions for the soil reactions on side and bottom of the pile are obtained. Further, combined with the obtained reactions, the differential equation for the pile vertically vibrating in the soil is established. The axisymmetrical analytical solution for vertical dynamic impedance of the pile head is then derived by solving the governing equation for the pile according to the compatibility condition between the pile and the soil. The proposed model is validated by comparing special cases of our model with the existing results. Finally, employing the solution developed, a parametric study has been undertaken to assess the effect of principal soil and pile parameters on the vertical dynamic impedance of the pile head. The results of the parametric study are also presented in this work.
2 Governing equations and general solutions
As shown in Fig. 1, an elastic floating cylinder pile with radius r0 and length L, which is subjected to a harmonic exciting force 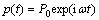
 with the frequency ω at its top (z=0), is embedded in a saturated viscoelastic soil layer with overlaying bedrock in thickness H. The modulus of the pile is EP, and the density is ρP. The volume fractions of the pore liquid and soil granule of the saturated viscoelastic soil layer are nL and nS, respectively, and nS+nL=1. The shear modulus of the soil granule is G, viscous damping coefficient is η,and the Possion ratio is υ. The macroscopic densities of the soil granule and pore liquid are ρS and ρL, respectively. Furthermore, it is assumed that the vibrations of the pile–soil system is infinitesimal, and the pile and the soil are connected tightly at their interfaces during vibration, namely, the displacements and stresses are continuous at the interfaces between the pile and the soil. And fs and RP in Fig. 1 denote the soil reactions on side and bottom of the pile, respectively.
with the frequency ω at its top (z=0), is embedded in a saturated viscoelastic soil layer with overlaying bedrock in thickness H. The modulus of the pile is EP, and the density is ρP. The volume fractions of the pore liquid and soil granule of the saturated viscoelastic soil layer are nL and nS, respectively, and nS+nL=1. The shear modulus of the soil granule is G, viscous damping coefficient is η,and the Possion ratio is υ. The macroscopic densities of the soil granule and pore liquid are ρS and ρL, respectively. Furthermore, it is assumed that the vibrations of the pile–soil system is infinitesimal, and the pile and the soil are connected tightly at their interfaces during vibration, namely, the displacements and stresses are continuous at the interfaces between the pile and the soil. And fs and RP in Fig. 1 denote the soil reactions on side and bottom of the pile, respectively.
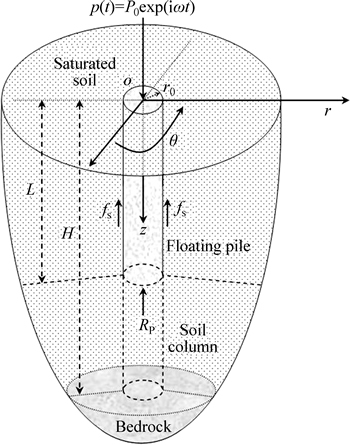
Fig. 1 A floating pile in a saturated viscoelastic soil layer overlaying bedrock
2.1 Dynamic governing equations for soil and mixed boundary conditions
Assuming that the soil granule and pore liquid are incompressible microscopically, and neglecting viscosity of the pore liquid and gravities of the soil granule and pore liquid, from the saturated porous medium model established by BOER and LIU [19–20], the three-dimensional dynamic governing equations for the saturated viscoelastic soil can be expressed as
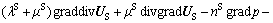
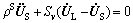 (1)
(1)
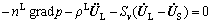 (2)
(2)
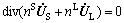 (3)
(3)
where 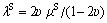 and
and 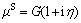 are the macroscopic complex Lame constants of the soil; Sv=
are the macroscopic complex Lame constants of the soil; Sv= 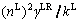 is the liquid–solid coupled coefficient which represents the interaction between soil granule and pore liquid, kL is the Darcy permeability coefficient of the soil, and
is the liquid–solid coupled coefficient which represents the interaction between soil granule and pore liquid, kL is the Darcy permeability coefficient of the soil, and 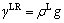 is the specific weight of the pore liquid; US and UL denote displacement vectors of the soil granule and pore liquid, respectively; p is the pore liquid pressure. (·) indicates the differentiation with respect to time variable t.
is the specific weight of the pore liquid; US and UL denote displacement vectors of the soil granule and pore liquid, respectively; p is the pore liquid pressure. (·) indicates the differentiation with respect to time variable t.
Introduce variables us and uL to denote the radial displacements of the soil granule and pore liquid, respectively, wS and wL the vertical displacements of the soil granule and pore liquid, respectively, and wP the vertical displacement of the pile. When the pile is in harmonic vertical vibration with exp(iωt), the soil also vibrates harmonically with exp(iωt). Hence, us= Usexp(iωt), uL=ULexp(iωt), ws=Wsexp(iωt), wL=WLexp(iωt), wP=WPexp(iωt), p=Pexp(iωt),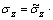
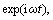
 Taking the axisymmetrical condition of the pile–soil system and above-mentioned expressions into account, Eqs. (1)–(3) can be deduced as
Taking the axisymmetrical condition of the pile–soil system and above-mentioned expressions into account, Eqs. (1)–(3) can be deduced as
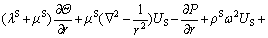
 (4)
(4)
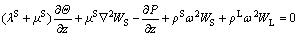 (5)
(5)
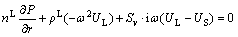 (6)
(6)
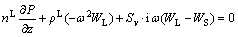 (7)
(7)
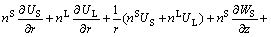
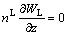 (8)
(8)
where  and
and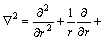
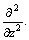
For the sake of convenience in the following analyses, we introduce dimensionless parameters and variables as follows: 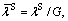
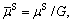
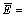
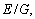

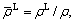
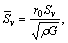


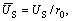
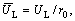
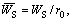
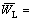
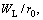
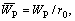
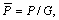
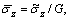
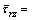
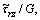
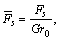
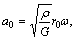 in which
in which 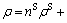
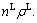
After introducing the dimensionless parameters and variables, Eqs. (4)–(8) can be written as
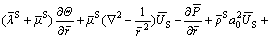
 (9)
(9)
 (10)
(10)
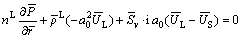 (11)
(11)
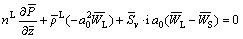 (12)
(12)

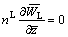 (13)
(13)
It is obtained from Eqs. (11) and (12) that
 (14)
(14)
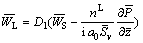 (15)
(15)
where 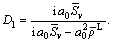
It is convenient that the simultaneous process between Eq. (9) and Eq. (10) can be expressed as 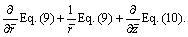 And then, substitute Eqs. (14) and (15) into it and yield
And then, substitute Eqs. (14) and (15) into it and yield
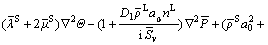
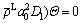 (16)
(16)
In a similar way, it is obtained from Eqs. (14) and (15) as 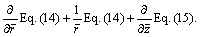 And then, substituting Eq. (13) into it, we have:
And then, substituting Eq. (13) into it, we have:
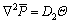 (17)
(17)
where 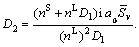
The constitutive relation of the stresses and displacements of the soil skeleton can be expressed as
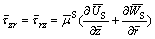 (18)
(18)
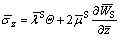 (19)
(19)
The pile–soil system in steady-state vibration should satisfy the following dimensionless boundary and continuity conditions:
1) The displacements and stresses should be zero at the infinite, namely
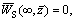
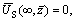
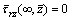 (20)
(20)
2) If the top surface of the soil is traction-free and permeable, then it requires
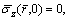
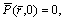
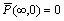 (21)
(21)
3) Assume that the bottom of the soil layer is rigid and impermeable, and then it requires
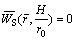 (22)
(22)
4) The pile/soil interface is impermeable, namely
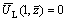 (23)
(23)
5) The radial displacement at the pile/soil interface is zero, namely
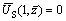 (24)
(24)
6) As the pile and the soil are connected tightly at their interfaces during vibration, the displacements and stresses are continuous at the interfaces between the pile and the soil. Then, we have
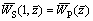 (25)
(25)
2.2 Fundamental solutions for soil reactions on side and bottom of pile
Setting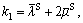
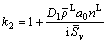 and
and 
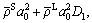 then Eq. (16) can be simplified as
then Eq. (16) can be simplified as
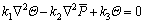 (26)
(26)
Equations (17) and (26) can be collectively expressed as
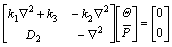 (27)
(27)
If Eq. (27) has nonzero solutions, the determinant of its coefficient matrix involving Laplace operator must be equal to zero. Namely,
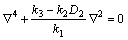 (28)
(28)
Equation (28) can be further written as
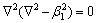 (29)
(29)
where 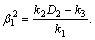
According to the separation theory of differential operator [24], define 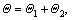 in which Θ1 and Θ2 satisfy the following equations, respectively:
in which Θ1 and Θ2 satisfy the following equations, respectively:
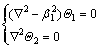 (30)
(30)
Assuming 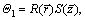 plug it into Eq. (30) and yield
plug it into Eq. (30) and yield
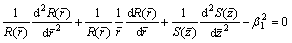 (31)
(31)
It can be obtained from Eq. (31) that
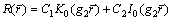 (32)
(32)
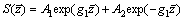 (33)
(33)
where 
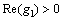 and
and 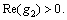
Thus
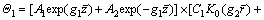
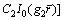 (34)
(34)
Similarly, we can get
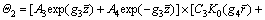
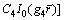 (35)
(35)
where I0(·) and K0(·) are the first and second kinds of modified Bessel functions, respectively. A1, A2, A3, A4, C1, C2, C3 and C4 are undetermined coefficients. And 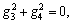
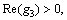
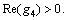
Therefore
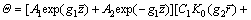
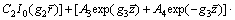
 (36)
(36)
In a similar way, it can be obtained that
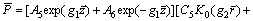
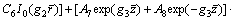
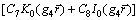 (37)
(37)
where A5, A6, A7, A8, C5, C6, C7 and C8 are undetermined coefficients.
It can be identified from the boundary conditions, Eqs. (20) and (21), that
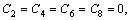
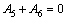 ,
, 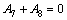 .
.
Substituting them into Eqs. (36) and (37), one obtains:

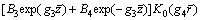 (38)
(38)
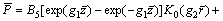
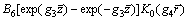 (39)
(39)
where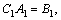

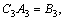
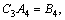
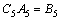 and
and 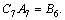
The substitution for Eqs. (38) and (39) into Eqs. (17) and (26) results in  and
and 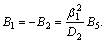
Thus, Eqs. (38) and (39) can be simplified as
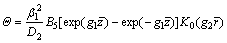 (40)
(40)

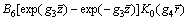 (41)
(41)
Equations (9) and (10) can be further expressed as

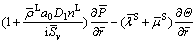 (42)
(42)
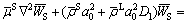
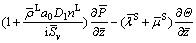 (43)
(43)
The homogeneous equation of Eq. (42) is
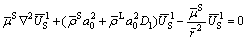 (44)
(44)
Defining 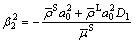 leads to
leads to
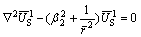 (45)
(45)
The solution for Eq. (45) can be easily obtained as
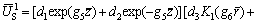
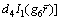 (46)
(46)
where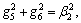
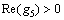 and
and 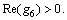 d1, d2, d3 and d4 are undetermined coefficients.
d1, d2, d3 and d4 are undetermined coefficients.
It can be derived from the boundary conditions Eq. (20) that d4=0. Thus, it has
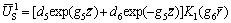 (47)
(47)
where d5=d1d3 and d6=d2d3.
Substituting Eqs. (40) and (41) into Eq. (42) yields

 (48)
(48)
The particular solution of Eq. (48) can be assumed as
 (49)
(49)
The substitution of Eq. (49) into Eq. (48) results in
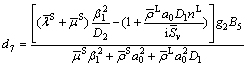 (50)
(50)
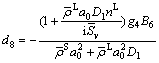 (51)
(51)
Thus, the solution of Eq. (42) is
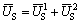
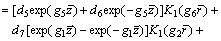
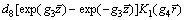 (52)
(52)
Similarly, the homogeneous equation of Eq. (43) is
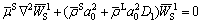 (53)
(53)
Setting 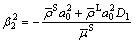 yields
yields
 (54)
(54)
The general solution of Eq. (54) is
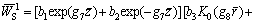
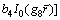 (55)
(55)
where 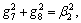
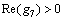 and
and 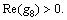 b1, b2, b3 and b4 are undetermined coefficients.
b1, b2, b3 and b4 are undetermined coefficients.
It can be obtained from the boundary condition Eq. (20) that b4=0. Defining b5=b1b3 and b6=b2b3 results in
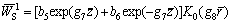 (56)
(56)
Substituting Eqs. (40) and (41) into Eq. (43), one obtains
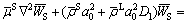
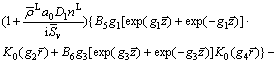
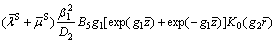 (57)
(57)
Similarly, the particular solution of Eq. (57) can be assumed as

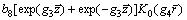 (58)
(58)
Plugging Eq. (58) into Eq. (57) leads to
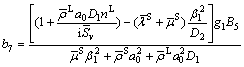 (59)
(59)
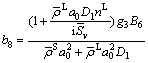 (60)
(60)
Thus, the solution of Eq. (43) is
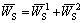
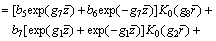
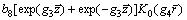 (61)
(61)
Substituting 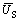 and
and 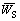 into
into 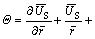
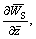 one obtains
one obtains 
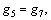
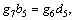
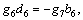
 and
and 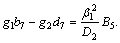
It can be derived from the boundary condition Eq.(21) that b5=b6 and d5=–d6.
Then, we can get
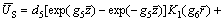
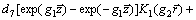
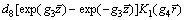 (62)
(62)
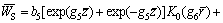
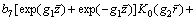
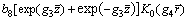 (63)
(63)
Plugging Eqs. (41), (62) and (63) into Eqs. (14) and (15) yields
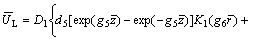
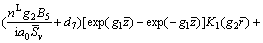
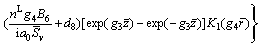 (64)
(64)
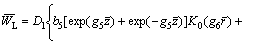
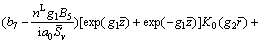
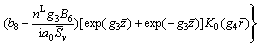 (65)
(65)
The substitution for Eq. (63) into the boundary condition (22) results in
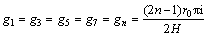 (66)
(66)
where gn is a unified symbol.
Plugging Eqs. (62) and (64) into the boundary conditions Eqs. (23) and (24) yields
 (67)
(67)
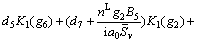
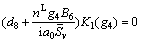 (68)
(68)
It can be obtained from Eqs. (67) and (68) that
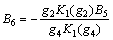 (69)
(69)
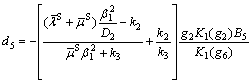 (70)
(70)
The shear stress of the soil at pile/soil interface is
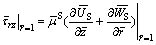
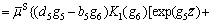
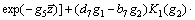
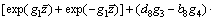
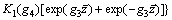 (71)
(71)
Then, the soil reaction fs on the pile side can be obtained as
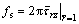 (72)
(72)
From superposition principle, the reaction fs can be written as
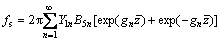 (73)
(73)
where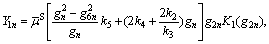
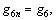
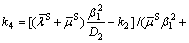

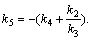
In a similar way, the vertical displacement 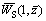 of the soil granule at pile/soil interface can be expressed as
of the soil granule at pile/soil interface can be expressed as
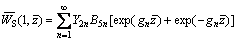 (74)
(74)
where 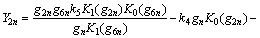
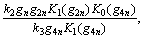 and
and 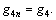
The dimensionless axial force of the soil pillar in vertical projection zone of the pile can be obtained as
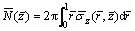 (75)
(75)
Similarly,  can be written as
can be written as
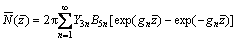 (76)
(76)
where
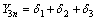
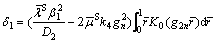
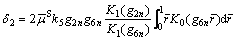
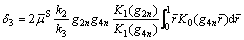
Then, when we put 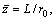 the soil reaction RP on the pile bottom can be determined as
the soil reaction RP on the pile bottom can be determined as
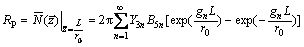 (77)
(77)
2.3 Vertical dynamic impedance of pile head
As shown in Fig. 1, using the soil reactions derived above, the dimensionless dynamic governing equation for the pile can be established as
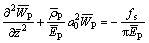 (78)
(78)
And the pile satisfies the following boundary conditions:
1) At the pile top, we have
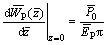 (79)
(79)
2) At the pile bottom, we have
 (80)
(80)
where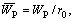
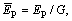
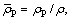
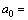
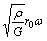 and
and 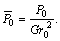
The general solution of the homogeneous equation of Eq. (78) is
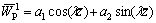 (81)
(81)
where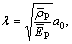 and a1 and a2 are undetermined coefficients.
and a1 and a2 are undetermined coefficients.
The particular solution of Eq. (78) can be assumed as
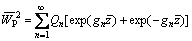 (82)
(82)
where Qn is undetermined coefficient.
Substituting Eq. (82) into Eq. (78) yields
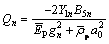 (83)
(83)
Therefore, the solution of Eq. (78) is
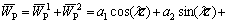
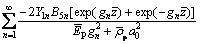 (84)
(84)
The substitution for Eqs. (74) and (84) into the continuity condition (25) results in
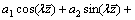
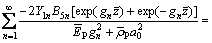
 (85)
(85)
With the orthogonality of functions 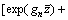
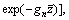 it can be deduced from Eq. (85) that
it can be deduced from Eq. (85) that
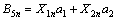 (86)
(86)
where
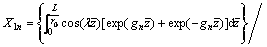
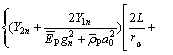

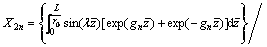
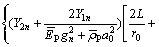

Then, Eq. (84) can be expressed as
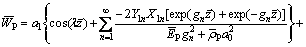
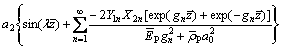 (87)
(87)
From the substitution of Eq. (87) into the boundary conditions Eqs. (79) and (80), one obtains
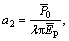
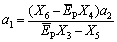 (88)
(88)
where
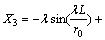
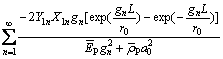
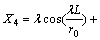
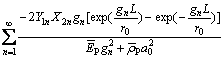
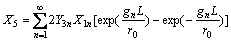
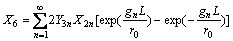
The normal stress at arbitrary point of the pile can be derived as
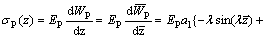
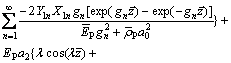
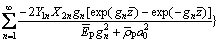 (89)
(89)
Hence, the vertical dynamic impedance of the pile head can be defined as
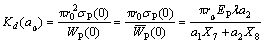 (90)
(90)
where 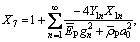
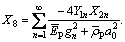
Defining the dimensionless form of  as
as
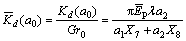 (91)
(91)
Introduce 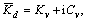 in which
in which  represents the actual dynamic stiffness, and
represents the actual dynamic stiffness, and 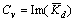 is the damping caused by waves radiation in the pile–soil system and relative movement between the pore liquid and the soil granule.
is the damping caused by waves radiation in the pile–soil system and relative movement between the pore liquid and the soil granule.
3 Numerical results and discussion
In this section, numerical computations are conducted to validate the accuracy of the solution and investigate the characteristics on vertical vibration of the pile. Unless otherwise stated, the following parameter values are employed: G=20 MPa, υ=0.2, nL=0.4, ρS=1800 kg/m3, ρL=1000 kg/m3, kL=9×10–7 m/s, EP= 20 GPa, ρP=2500 kg/m3, and r0=0.25 m. In the following analysis, for the sake of convenience in contrast, the stiffness of the pile head is normalized as Kv/K0, in which 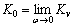 denotes the static stiffness at the pile head.
denotes the static stiffness at the pile head.
3.1 Verification of solution
This solution is verified by comparing with LIU and YANG’s solution [25] for an end bearing pile in saturated viscoelastic soil. Given L=H, the problem of this work is degenerated to the vertical vibration of an end bearing pile in saturated viscoelastic soil. The dynamic impedance of the degenerated solution of this work and LIU and YANG’s solution is compared with varying the length-to-radius ratio of the pile l=L/r0 (shown in Fig. 2, η=0.01). It can be noted that for different l, the degenerated solution of this work agrees well with the solution proposed by LIU and YANG.

Fig. 2 Comparison of results of present work and Ref. [25]:
WU [26] studied the vertical dynamic response of a floating pile in single-phase soil. Given 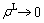 and
and 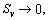 the solution in this work is reduced to that of a floating pile in single-phase soil and compared with WU’s solution [26] for varying l (shown in Fig. 3,
the solution in this work is reduced to that of a floating pile in single-phase soil and compared with WU’s solution [26] for varying l (shown in Fig. 3, 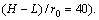 For different l, excellent agreement is observed between the reduced solution in this work and WU’s solution. Therefore, according to the results in Figs. 2 and 3, the validity of the present solution is confirmed. And the solution in this work can be considered as an extension of both LIU and YANG’s solution and WU’s solution.
For different l, excellent agreement is observed between the reduced solution in this work and WU’s solution. Therefore, according to the results in Figs. 2 and 3, the validity of the present solution is confirmed. And the solution in this work can be considered as an extension of both LIU and YANG’s solution and WU’s solution.
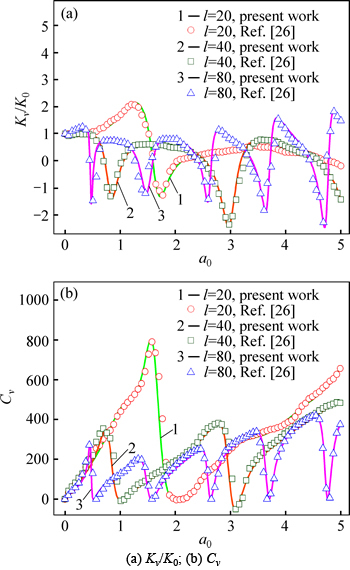
Fig. 3 Comparison of results of present work and WU [26]:
3.2 Parametric study for dynamic impedance of pile head
The dynamic impedance of the pile head is often employed to estimate the vibration resistance of pile foundations and analyze the vibration characteristics of pile–soil system. The real part of the dynamic impedance is the real stiffness, while the imaginary part is the damping which reflects the energy dissipation of the pile–soil system. The stiffness and damping are influenced by many parameters such as the relative depth of pile-bedrock, liquid–solid coupled coefficient, length- to-radius ratio of pile, relative rigidity of pile–soil, and viscous damping coefficient of soil. The effects of them are shown in Figs. 4–9. It is noted that both the stiffness and damping of the pile head fluctuate steeply with the excitation frequency. Resonances occur at the natural frequencies, and the oscillation amplitudes of the stiffness and damping increase as the excitation frequency increases.
Figure 4 shows the comparison of the results of present work and end-bearing pile [25] and half space [6]. It can be easily seen that compared with the results of end-bearing pile [25] and half space [6], the results of present work are notably different and depend on the relative location of bedrock intensely. The concrete effect of relative location of the bedrock on the dynamic impedance of the pile head is shown in Fig. 5 (η=0.01, 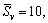 l=20, and EP/G=1000). It can be found that due to the dynamic interaction between the pile and the soil under the pile bottom, there exist many differences between the results of the floating pile and the end bearing pile (H/L=1), whether the variation trend or oscillation amplitude, and the relative depth of pile–bedrock has a remarkable influence on the dynamic impedance of the pile head against the excitation frequency. When the pile length is certain, in the low-frequency range, the resonance frequencies and amplitudes of the stiffness decrease gradually with the augment of the relative depth of pile–bedrock, also the resonance frequencies of the damping, but its resonant amplitudes firstly decrease and then increase. In the high-frequency range, the resonance frequencies of the stiffness and damping vary slightly while their oscillation amplitudes at resonance frequencies decrease steeply as the relative depth of pile–bedrock increases. It is not difficult to find that the smaller the spacing between the bedrock and the pile bottom is, the more pronounced the effect of the bedrock on the dynamic impedance of the pile head is.
l=20, and EP/G=1000). It can be found that due to the dynamic interaction between the pile and the soil under the pile bottom, there exist many differences between the results of the floating pile and the end bearing pile (H/L=1), whether the variation trend or oscillation amplitude, and the relative depth of pile–bedrock has a remarkable influence on the dynamic impedance of the pile head against the excitation frequency. When the pile length is certain, in the low-frequency range, the resonance frequencies and amplitudes of the stiffness decrease gradually with the augment of the relative depth of pile–bedrock, also the resonance frequencies of the damping, but its resonant amplitudes firstly decrease and then increase. In the high-frequency range, the resonance frequencies of the stiffness and damping vary slightly while their oscillation amplitudes at resonance frequencies decrease steeply as the relative depth of pile–bedrock increases. It is not difficult to find that the smaller the spacing between the bedrock and the pile bottom is, the more pronounced the effect of the bedrock on the dynamic impedance of the pile head is.
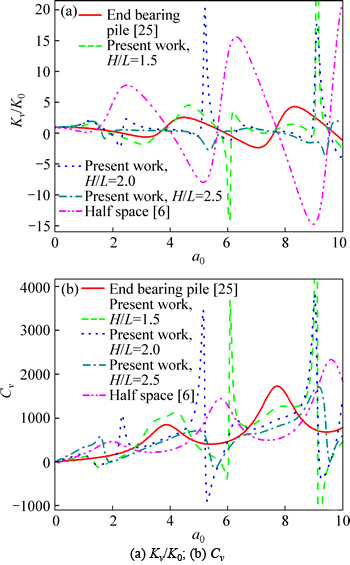
Fig. 4 Comparison of results of present work and other cases [6, 25]:
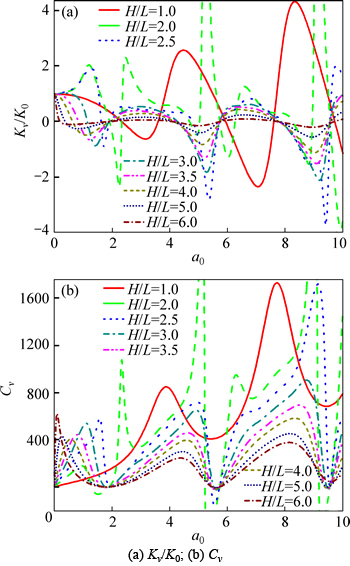
Fig. 5 Effect of relative depth of pile–bedrock on dynamic impedance:
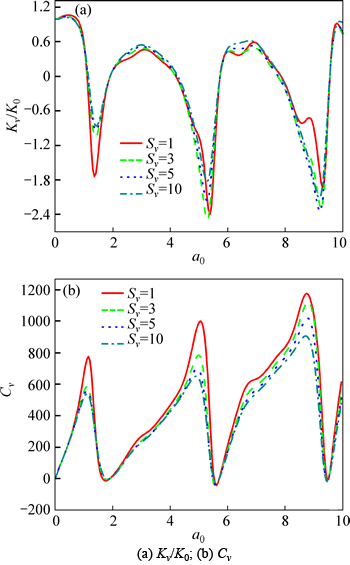
Fig. 6 Effect of liquid-to-solid coupled coefficient on dynamic impedance:
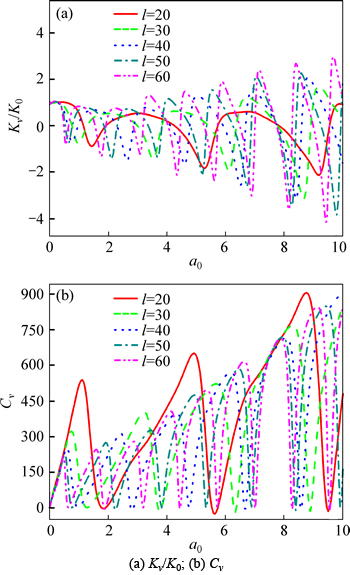
Fig. 7 Effect of length-to-radius ratio of pile on dynamic impedance:

Fig. 8 Effect of relative rigidity of pile–soil on dynamic impedance:
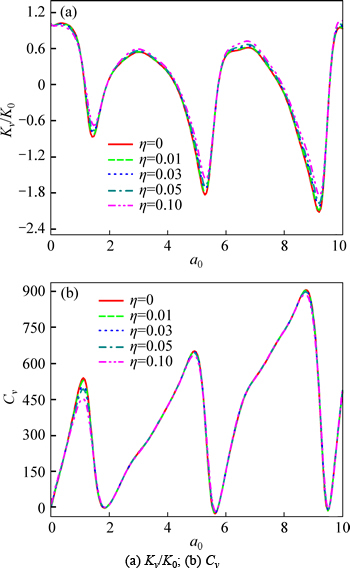
Fig. 9 Effect of viscous damping coefficient of soil on dynamic impedance:
The effect of liquid–solid coupled coefficient on the dynamic impedance of the pile head is shown in Fig. 6 (η=0.01, H/L=3, l=20, and EP/G=1000). It can be seen that with the increase of the liquid–solid coupled coefficient, the resonance amplitudes of the stiffness decrease in low-frequency range, but firstly increase and then decrease in high-frequency range. And the damping gradually decreases with the increase of the liquid–solid coupled coefficient. And the resonance frequencies of both the stiffness and damping show negligible change as the liquid–solid coupled coefficient increases.
Figure 7 shows the effect of the length-to-radius ratio of pile on the dynamic impedance of the pile head (η=0.01, 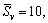 (H–L)/r0=40, and EP/G=1000). It can be found that when the spacing between the bedrock and the pile bottom is certain, with the augment of the length-to-radius ratio of pile, the resonance frequencies of the stiffness show significant decrease, but the oscillation amplitudes at resonance frequencies decrease slightly. The resonance frequencies and amplitudes of the damping decrease steeply with it. Especially, different with results of end bearing pile problem [1–5], there is not the concept of critical pile length for the floating pile in saturated soil layer overlaying bedrock.
(H–L)/r0=40, and EP/G=1000). It can be found that when the spacing between the bedrock and the pile bottom is certain, with the augment of the length-to-radius ratio of pile, the resonance frequencies of the stiffness show significant decrease, but the oscillation amplitudes at resonance frequencies decrease slightly. The resonance frequencies and amplitudes of the damping decrease steeply with it. Especially, different with results of end bearing pile problem [1–5], there is not the concept of critical pile length for the floating pile in saturated soil layer overlaying bedrock.
The effect of the relative rigidity of pile–soil on the dynamic impedance of the pile head is shown in Fig. 8 (η=0.01, 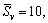 H/L=3, and l=20). It can be seen that with the relative rigidity of pile-soil increasing, the resonance frequencies of both the stiffness and damping significantly increase, yet the resonant amplitudes of the stiffness first prominently increase and then slightly decrease, as well as those of the damping in low- frequency range. In high-frequency scope, the resonance amplitudes of the damping increase steeply with it.
H/L=3, and l=20). It can be seen that with the relative rigidity of pile-soil increasing, the resonance frequencies of both the stiffness and damping significantly increase, yet the resonant amplitudes of the stiffness first prominently increase and then slightly decrease, as well as those of the damping in low- frequency range. In high-frequency scope, the resonance amplitudes of the damping increase steeply with it.
Figure 9 shows the effect of the viscous damping coefficient of soil on the dynamic impedance of the pile head (l=20, H/L=3, 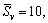 and EP/G=1000). It can be found that with the increase of the viscous damping coefficient of soil, the resonance frequencies of both the stiffness and damping show little change, but the resonant amplitudes of the stiffness gradually decrease, and those of the damping in low-frequency range also decrease. In high-frequency range, those for the damping show negligible variation with it.
and EP/G=1000). It can be found that with the increase of the viscous damping coefficient of soil, the resonance frequencies of both the stiffness and damping show little change, but the resonant amplitudes of the stiffness gradually decrease, and those of the damping in low-frequency range also decrease. In high-frequency range, those for the damping show negligible variation with it.
4 Conclusions
1) Comparison with the existing solutions confirms the accuracy of the proposed formulations and also the numerical computation involved. Both the vertical vibration of an end bearing pile in saturated soil and a floating pile in single-phase soil overlaying bedrock are special cases of the solutions as the pile length equals the soil thickness, and the liquid–solid coupled coefficient and density of pore liquid tend to be zero, respectively. Consequently, appropriately varying parameters, some extended problems on them can be conveniently investigated by means of the presented solution.
2) The dynamic impedance for vertical vibration of the floating pile in saturated viscoelastic soil overlaying bedrock fluctuates with the excitation frequency and shows noticeable resonant phenomenon. But due to the effect of the bedrock, the change trend and amplitude for parameters variation are different and more complicated compared with previous results of end bearing pile and half space.
3) Parametric study illustrates that the principal influence factors affecting the pile’s dynamic impedance are the location of bedrock relative to pile, physical and geometrical properties of pile–soil system, and applied loads. The dynamic impedance at the pile head will be evidently different at varying depth of bedrock relative to pile, liquid–solid coupled coefficient, length-to-radius ratio of pile, rigidity of pile relative to soil, viscous damping coefficient of soil and excitation frequency. Especially, it should be mentioned that the impedance of the pile head significantly depends on relative location of the bedrock, and the smaller the spacing between the bedrock and the pile bottom is, the more remarkable the effect of the bedrock on it is.
References
[1] YU Jun, CHEN Hai-ming, YANG Zhao, LIU Cheng. Dynamic analysis of vertical loaded single pile in multilayered saturated soils [J]. Computational Structural Engineering, 2009(1): 761–769.
[2] WANG Kui-hua, ZHANG Zhi-qing, LEO Chin-jian, XIE Kang-he. Dynamic torsional response of an end bearing pile in saturated poroelastic medium [J]. Computers and Geotechnics, 2008, 35: 450–458.
[3] WANG Kui-hua, ZHANG Zhi-qing, LEO Chin-jian, XIE Kang-he. Dynamic torsional response of an end bearing pile in transversely isotropic saturated soil [J]. Journal of Sound and Vibration, 2009, 327: 440–453.
[4] HU Wen-tao, XIA Tang-dai, ZHANG Zhi-qing. Dynamic torsional response of pre-strained end bearing pile embedded in pre-strained isotropic saturated soil medium [J]. Applied Mathematics and Mechanics, 2013, 34(12): 1521–1534.
[5] LIU Han-long, ZHENG Chang-jie, DING Xuan-ming, QIN Hong-yu. Vertical dynamic response of a pipe pile in saturated soil layer [J]. Computers and Geotechnics, 2014, 61: 57–66.
[6] ZENG X, RAJAPAKSE R K N D. Vertical vibrations of a rigid disk embedded in a poroelastic medium [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1999, 23: 2075–2095.
[7] JIN Bo, ZHOU D, ZHONG Z. Lateral dynamic compliance of pile embedded in poroelastic half space [J]. Soil Dynamics and Earthquake Engineering, 2001, 21: 519–525.
[8] LU Jian-fei, JENG Dong-sheng, NIE Wei-dong. Dynamic response of a pile embedded in a porous medium subjected to plane SH waves [J]. Computers and Geotechnics, 2006, 33: 404–418.
[9] LU Jian-fei, XU Bin, WANG Jian-hua, JENG Dong-sheng. Dynamic responses of a pile embedded in a layered poroelastic half-space to a harmonic axial loading [J]. Acta Mech, 2009, 207: 29–49.
[10] CAI Yuan-qiang, CHEN Gang, XU Chang-jie, WU Da-zhi. Torsional response of pile embedded in a poroelastic medium [J]. Soil Dynamics and Earthquake Engineering, 2006, 26: 1143–1148.
[11] WANG Guo-cai, GE Wei, PAN Xiao-dong, WANG Zhi. Torsional vibrations of single piles embedded in saturated medium [J]. Computers and Geotechnics, 2008, 35: 11–21.
[12] ZHOU Xiang-lian, WANG Jian-hua, JIANG Ling-fa, XU Bo. Transient dynamic response of pile to vertical load in saturated soil [J]. Mechanics Research Communications, 2009, 36: 618–624.
[13] XU Bin, LU Jian-fei, WANG Jian-hua. Numerical analysis of the isolasion of the vibration due to Rayleigh waves by using pile rows in the poroelastic medium [J]. Arch Appl Mech, 2010, 80: 123–142.
[14] CAI Yuan-qiang, CHEN Gang, LIU Fei-yu. Torsional pile subjected to transient loading in viscoelastic poroelastic medium [C]// International Conference on Computational Science. 2007, 1188– 1196.
[15] CHEN Gang, CAI Yuan-qiang, LIU Fei-yu, SUN Hong. Dynamic response of a pile in a transversely isotropic saturated soil to transient torsional loading [J]. Computers and Geotechnics, 2008, 35: 165–172.
[16] LI Qiang, Zheng Hui, WANG Kui-hua. Analytical solution and its application of vertical vibration of a friction pile in saturated soil [J]. Engineering Mechanics, 2011, 28(1): 157–170. (in Chinese)
[17] EDELMAN I, WILMANSKI K. Asymptotic analysis of surface waves at vacuum/porous medium and liquid/porous medium interfaces [J]. Continuum Mech Thermodyn, 2002, 14: 25–44.
[18] BOER D R. Some issues in the macroscopic porous media theory [M]. Siekmann-Festschrift: University-GH Essen, 1995: 310-323.
[19] BOER D R, LIU Z F. Propagation of acceleration waves in incompressible saturated porous solids [J]. Transport in Porous Media, 1995, 21: 163–173.
[20] BOER D R, LIU Z F. Plane waves in a semi-infinite fluid saturated porous medium [J]. Transport in Porous Media, 1994, 16: 147–173.
[21] BOER D R, LIU Z F. Growth and decay of acceleration waves in incompressible saturated porous elastic solids [J]. J Appl Math Mech, 1996, 76(6): 341–347.
[22] LIU Zhan-fang, LI De-yuan, YAN Bo. Inhomogeneous plane waves in a saturated porous medium [J]. Rock and Soil Mechanics, 1999, 20(4): 31–35. (in Chinese)
[23] YANG Xiao, CHE Jing-lan. Plane waves and their energy dissipations in a saturated viscoelastic porous medium [J]. Chinese Journal of Theoretical and Applied Mechanics, 2005, 37(5): 579–585. (in Chinese)
[24] SENJUNTICHAI T, RAJAPAKSE RKND. Transient response of a circular cavity in a poroelastic medium [J]. Int J Numer Anal Meth Geomech, 1993, 17: 357–383.
[25] LIU Lin-chao, YANG Xiao. Study of vertical coupled vibrations of piles in saturated soils using porous medium theory [J]. China Civil Engineering Journal, 2009, 42(9): 89–95. (in Chinese)
[26] WU Wen-bing. Vertical vibration theory of pile-soil system based on fictitious soil pile method and its application [D]. Hangzhou: Zhejiang University, 2012. (in Chinese)
(Edited by YANG Bing)
Foundation item: Projects(50809009, 51578100) supported by the National Natural Science Foundation of China; Projects(3132014326, 3132015095) supported by the Fundamental Research Funds for the Central Universities of China
Received date: 2014-12-04; Accepted date: 2015-04-29
Corresponding author: CUI Chun-yi, Associate Professor, PhD; Tel: +86–411–84723186; E-mail: cuichunyi@dlmu.edu.cn
Abstract: An axisymmetrical analytical solution is developed to investigate the vertical time-harmonic vibration of a floating pile in a saturated viscoelastic soil layer overlaying bedrock. The soil is described by porous medium model established by Boer, while the pile is described by a beam vibration theory. By using separation theory of differential operator and variables to solve the dynamic governing equations for the soil, the fundamental solutions for the soil reactions on side and bottom of the pile are obtained. The dynamic impedance of the pile head is then derived by solving the vibration equation for the pile according to the compatibility condition between the pile and the soil. The proposed model is validated by comparing special cases of our model with the existing results. Numerical examples are presented to analyze the vibration characteristics of the pile.
- Vertical vibration of a floating pile in a saturatedviscoelastic soil layer overlaying bedrock


