基于粒子群优化算法和ANFIS的矿体品位插值-有色金属在线

地质模型在矿产勘探与开发中具有重要作用，但在矿山生产实践中，由于成本和技术等诸多因素影响，很难获得整个区块的地质数据，而且传统插值方法依靠经验确定参数有很大局限性。提出将粒子群优化算法(PSO)和自适应神经模糊推理系统(ANFIS)应用到矿体品位插值中，利用粒子群优化算法的快速搜索能力，神经网络的学习机制和模糊系统的语言推理能力等优势构建PSO-ANFIS品位插值模型，并借助MATLAB生成571组样本数据作为输入空间对模型进行训练，其中每一个训练样本由待估点三维坐标及真实值和其周围8个样品点组成，最后用训练后的PSO-ANFIS模型对待估点进行品位插值，并与距离幂次反比插值法进行对比，其均方根误差(RMSE)提高了近15%，验证了该模型的可行性和有效性。

关键词：

矿石品位；空间插值；粒子群优化算法；自适应模糊神经推理系统；优化；

文章编号：1004-0609(2019)-01-0194-09　　中图分类号：TD853　　文献标志码：A

矿体品位模型的构建从矿山勘探阶段开始贯穿矿山开采的整个周期，基于原始勘探钻孔数据构建的品位模型用来计算矿石储量和品位空间分布情况，用有限的样本数据集进行矿床储量计算^[1]，是矿床开采整个过程中的核心问题，其中品位空间插值是计算矿床储量的重要步骤之一。

矿体品位插值本质上是根据周围已知信息预测待估点品位的非参数回归问题，待估点品位与周围样品品位、样品距待估点距离、样品点所属岩性等因素有关，是包含大量自变量的模糊或灰色空间测度问题。自20世纪80年代利用能高精度从输入空间向输出空间完成任何映射的机器学习^[2-4]来研究非线性数学模型构建解决矿床品位插值问题，引起了学者们的关注，谭正华等^[5]利用地质统计学中变异函数理论分析元素品位空间变异性，改进了距离反比加权插值方法，李娟等^[6]使用与自组织神经网聚类相结合的支持向量回归机预测模型对矿体体素品位进行插值，贾明涛等^[7]针对传统BP神经网络的不足，着重研究矿床品位估值的径向基函数神经网络构建技术，李翠平等^[8-9]利用遗传算法全局搜索的优势将支持向量机(SVM)^[10-11]和遗传算法(GA)^[12]集成应用到矿体品位插值问题中，说明了该插值方案的可行性，同时通过分析泰森多边形性质，建立了跟距离有相关性的品位插值关系，解决了泰森多边形法的空间品位插值问题；周仲礼等^[13]通过采用改进的模拟退火蚁群算法作为径向基神经网络径向基层的训练法确定更为优化的初始中心，增强径向基网络的性能。但是这些品位插值学方法有的需要对研究对象做出了各种假定，其插值结果受经验与相关知识的掌握程度影响较大，限制了其效果的充分发挥和应用，有的在对神经网络进行训练过程中容易出现收敛速度很慢、迭代次数较多，或最小误差陷入局部最小不能达到全局最优的情况，且人工神经网络类似一个黑箱，缺少透明度，不能很好地表达人脑的推理功能。

为克服传统插值方法依靠经验确定参数的局限性，本文作者提出将粒子群优化算法(PSO)^[14-15]和自适应模糊神经推理系统(ANFIS)^[16]应用到矿体品位插值中，利用粒子群优化算法快速搜索能力，神经网络的学习机制和模糊系统的语言推理能力优势构建PSO-ANFIS^[17-20]模型进行品位插值，同时利用距离幂反比法交叉验证模型的可行性和有效性。

1 粒子群优化的自适应神经模糊推理系统算法

1.1 粒子群优化算法(PSO)

粒子群算法(PSO)是通过模拟鸟群捕食行为设计的一种智能算法，它的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解，目前在神经网络训练、函数优化、模糊系统控制等领域已被广泛应用，它的优势如下。

1) 依靠粒子速度完成搜索，并且在迭代进化中只有最优的粒子把信息传递给其他粒子，搜索速度快。

2) 具有强大记忆功能，粒子群体的历史最好位置可以记忆并传递给其他粒子。

3) 结构简单，需调整的参数少，易于工程实现。

4) 采用实数编码，所求问题解的变量个数直接作为粒子的维数。

鸟被抽象为没有质量和体积的点，并延伸到N维空间，粒子i在N维空间的位置表示为矢量x_i=(x₁，x₂，…，x_N)，飞行速度表示为矢量v_i=(v₁，v₂，…，v_N)。PSO算法初始化为一群随机粒子，每个粒子都有通过目标函数决定的适应值，并且知道自己到目前为止发现的最好位置(p_best)和现在的位置X_i，然后通过迭代找到最优解，在每一次的迭代中，粒子通过跟踪两个“极值”(p_best，g_best)来更新自己，其结构如图1所示，在找到这两个最优值后，粒子通过下面的公式来更新自己的速度和位置：

(1)

图1 粒子群优化算法位置更新结构

Fig. 1 Location update structure of particle swarm optimization algorithm

(2)

式(1)和(2)中：i=1，2，3，…，N，N是此群中粒子的总数；v_i是粒子的速度；ω是惯性因子；r₁、r₂介于(0，1)之间的随机数；x_i是粒子的当前位置；c₁、c₂是学习因子；v_i的最大值为v_max (大于0)，如果v_i大于v_max，则v_i=v_max。

1.2 自适应神经模糊推理系统(ANFIS)

自适应神经模糊推理系统(ANFIS)是通过简单清晰方式将模糊逻辑表达出来以符合人类认知事物的习惯，同时将具有强大的自组织学习能力的神经网络镶嵌在模糊推理的每一步骤中，使神经网络的每一层都具有明确的物理意义，也使模糊规则和隶属度函数的参数调整具有自适应性，能很好解决数据建模问题，ANFIS以Sugeno模型为基础，设两输入单输出模型具有两条普通模糊if-then规则：

规则1：如果x是A₁，且y是B₁，则f₁=p₁x+q₁y+r₁；

规则2：如果x是A₂，且y是B₂，则f₂= p₂x+q₂x+q₂y+r₂。

其中：x、y为输入；A₁、B₁、A₂、B₂为模糊语言(如大或小)；f₁、f₂为规则输出；{p_j，q_j，r_j}(i=1，2，3，…)为结论参数集。

实现上述规则的ANFIS结构如图2所示。

图2 自适应神经模糊推理系统(ANFIS)结构

Fig. 2 Structure of adaptive neuro-fuzzy inference system (ANFIS)

第1层：运用隶属度函数对输入数据进行模糊化；

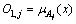，j=1，2

或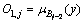，j=3，4 (3)

第2层：分别计算各个规则下的激励强度；

，j=1，2 (4)

第3层：计算第i条规则下激励强度占总激励强度的比值，使其生成归一化的激励强度；

，j=1，2 (5)

第4层：计算第i条规则对总输出的贡献比例；

，j=1，2 (6)

第5层：计算所有输入的总输出量。

，j=1，2 (7)

式中：x，y为输入；O_k_,i为各层各结点的输出(k=1，2，3，4，5；j=1，2)；和分别为x，y的

隶属度函数，；为前提参数集；

为各条规则的激励强度；为归一化激励强度；f_j为规则输出；{p_j，q_j，r_j}为结论参数集。

给定前提参数后，ANFIS的输出可以表示成结论参数的线性组合：

(8)

式中：列向量θ的元素构成结论参数集合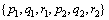，使用最小二乘法求解使值最小情况下结论参数向量的最佳估值θ，即

(9)

然后根据结论参数的辨识结果θ，根据下式计算ANFIS的估值输出f：

(10)

则计算出当前的前提参数和结论参数下的均方根误差(Root-mean-squire error，R)：

(11)

1.3 PSO-ANFIS模型算法

运用粒子群优化算法和最小二乘法对ANFIS的前提参数和结论参数进行优化，PSO-ANFIS算法的每一次学习过程皆包括前提参数学习阶段和结论参数学习阶段，其流程如图3所示，PSO-ANFIS算法的具体流程。

1) 当迭代次数为n=1时，在搜索空间随机初始化粒子群，第i个粒子位置向量为，速度向量为，其中1≤i≤m，1≤d≤D，m为粒子群大小，D为搜索空间维数也即是前提参数个数；

图3 PSO-ANFIS算法流程图

Fig. 3 Flowchart of PSO-ANFIS algorithm

2) 将每个粒子位置向量依次作为ANFIS的前提参数，根据公式(3)~(5)计算出所有规则的激励强度和归一化激励强度(1≤j≤l，l为规则数)；根据公式(8)计算得到系数矩阵A；然后采用最小二乘法辨识出结论参数，最后根据公式(10)~(11)计算出粒子所对应的ANFIS所产生的损失误差作为该粒子的适应度值；

3) 用每个粒子的当前适应度值与其本身最好适应度值进行比较，若，则，；

4) 用每个粒子的当前适应度值与粒子群的最好适应度值进行比较，若，则，；

5) 按照公式(1)~(2)更新每个粒子的速度和位置向量，n=n+1，返回第2步直到达到最大迭代次数。

2 基于PSO-ANFIS模型的品位插值

2.1 输入变量及个数的选取

构建基于粒子群优化算法和ANFIS的品位插值模型首先要设计和确定输入变量类型及个数，选定的输入变量应是对品位有重要影响的因素，由于输入变量的个数直接影响模型训练过程中的存储、计算复杂度、输入到输出映射函数的映射能力及所建模型对品位估值的精度，因此，合理选定输入变量的类型及个数异常重要，在三维地质模型空间中，某点的成矿模式、类型及所属岩性等因素决定着该点否含有有用元素，所以输入变量类型应包括彼此独立亦或对估值有较大影响的因素，同时对估值结果精度影响不大的因素可以忽略，既能减少由于输入变量因素过多导致模型训练计算复杂度增加的问题，又能准确地反映输入变量和输出变量之间的复杂关系。

根据地质勘探提交样品构建的地质数据库样品的分布情况，参考地质统计学等其他数学地质方法，采用球体8扇区搜索方法对输入变量进行选择与设定，每个扇区内有1个样品点，待估点周围均匀分布已知样品点，形成一种内插格局，其中每一个训练样本由待估点三维坐标及周围8个样品点和待估点的真实值组成。图4所示为八分圆的三维示意图。图5所示为八分圆二维形式四分圆示意图。

图4 八分圆的三维示意图

Fig. 4 Three-dimensional sketch of eight parts circle

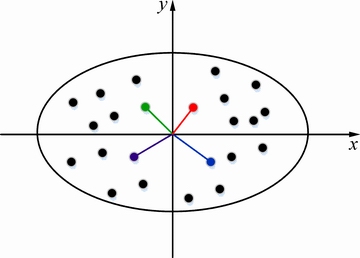
图5 八分圆二维形式示意图

Fig. 5 Two-dimensional sketch of eight parts circle

2.2 工程数据样本

为验证PSO-ANFIS品位插值结果的准确性，借助DIMINE采矿软件产生原始样本，如图6所示，同时用MATLAB对样本进行预处理，对每一个样品点，根据钻孔的实际分布情况设定搜索球体半径，将搜索球体沿其3个轴的垂直面分割得到8个扇区，并设置每个扇区数据个数为1，对每个扇区内的全部数据点按照距离待估点的远近排序，选取最近的样品点，用距离幂反比法对待估点进行估值，将每个待估点及选取的周边样品点信息全部输出到文件构成输入空间共571条，如表1所示，每个数据依次为待估点的XYZ坐标，附近的8个样品点以及待估点的真实品位信息，其中从上述571条数据中随机选取400条作为模型训练样本，其余的171条数据作为测试样本，在运用模型求解时对待估点坐标进行归一化处理，减小数据变化过大对结果影响。

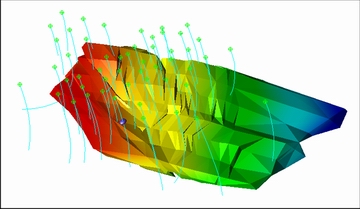
图6 矿体和钻孔数据库

Fig. 6 Orebody and drilling database

表1 工程数据样本

Table 1 Sample of engineering data

2.3 PSO-ANFIS品位插值模型及验证

根据品位插值的输入变量及个数的讨论，建立PSO-ANFIS模型，考虑到影响因素输入变量量纲上的差异，将样本数据按属性进行归一化处理，采用离差标准化对原始数据的线性变换，使结果值映射到[0-1]之间，其计算式(12)为

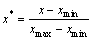(12)

式中：x_max为样本数据的最大值；x_min为样本数据的最小值。

通过改变粒子群算法的迭代次数m，最大粒子个数n，初始化权重W，权重下降速率W_dsmp以及参数c₁和c₂，对自适应模糊神经推理系统(ANFIS)的前提参数进行优化，其详细参数见表2所示。

表2 PSO-ANFIS品位插值模型参数

Table 2 PSO-ANFIS grade interpolation model parameters

最后利用上述工程样本数据及粒子群优化算法对自适应模糊神经推理系统(ANFIS)进行训练，通过分析工程数据及模糊神经推理系统可知，模型输入总共有11个变量，由于采用模糊c均值聚类产生FIS结构，此次设置模糊规则为10，每个变量产生10个分类，总共有11×10个模糊隶属函数进行优化，每个高斯隶属函数包含两个前提参数，最终得到每个变量的隶属函数曲线，只显示了其中的4个，如图7(a)~(d)所示，也即是确定了模糊神经推理系统的前提参数。

同时，模型的输出为1个结果，根据模糊神经推理系统(ANFIS)的结构可知，在给定前提参数后，ANFIS的输出可以表示成结论参数的线性组合，每条规则有12个结论参数，分别用p，q，r表示样本数据x，y，z坐标的结论参数，用s，t，u，v，w，n，k表示每个样本数据的8个周围采样点的结论参数，用a表示模糊规则松弛的结论参数，见表3所示。

通过粒子群优化算法优化得到模糊神经推理系统的前提参数和结论参数，则PSO-ANFIS模型就能确定，同时训练的结果如图8所示，其中图8(a)所示为预测输出品位与目标品位的对比分析图，图8(b)所示为每个训练样本的输出品位和目标品位的偏差图，图8(c)所示为偏差值的累积频率直方图，由图可知训练样本的均方根误差(R)为1.8454，均方误差(R′)为3.4056，同时从偏差的统计分析可以看出，偏差大都集中在0附近。

2.4 不同插值模型结果比较

为说明PSO-ANFIS插值模型应用在品位插值中的可靠性，采用地球科学领域比较常用的多元插值方法——距离幂次反比法进行对比分析，该方法是通过分析空间散乱点的已知值计算待估点的值，它是邻近点距离倒数的函数，对于待估点x的估计值Z一般形式(Z(x))为式(13)：

(13)

式中：x为插值点；x_i为已知点；Z_i为已知点x_i处的值；N为用于插值的已知点的总数；d为已知点x_i到未知点x的距离；权重W_i随着与未知点距离的增加而减小，p值越大，则距离未知点越近，对未知点的值影响也越大。

对于优化的PSO-ANFIS模型和距离幂次反比法品位插值模型，分别利用171个测试数据样本在MATALB中进行求解验证，其求解结果如图9所示。图中有3条曲线，分别为距离次反比法求解的待估点品位情况，待估点的真实品位信息和利用PSO-ANFIS模型求解的品位信息，3条曲线的走势大致相同，由于真实值存在部分较大的噪声点，对结果会有部分影响，整体来看符合要求。

从各个模型的预测结果来看，整体满足要求，需要进一步定量分析其均方根误差(R)，来更清晰准确地衡量预测值同真值之间的偏差情况，其中均方根误差越小，说明预测值与真值越接近，效果越好，从结果来看PSO-ANFIS模型测试数据R为1.8397优于距离幂次反比法的2.1568，具体求解结果见表4。

图7 输入变量的高斯隶属度曲线

Fig. 7 Gaussian membership curves of input variables

表3 PSO-ANFIS模型的结论参数

Table 3 Conclusion parameters of PSO-ANFIS model

同时从图10中可以直观看出，无论对于训练数据，测试数据还是所有的数据样本而言PSO-ANFIS模型优于距离幂次反比法，R值都比距离幂次反比插值法小，其中测试数据的R提高了近15%，因此，总体而言，基于粒子群优化算法和模糊神经推理系统(PSO-ANFIS)模型的矿体品位插值效果将更好，准确度更高。

图8 PSO-ANFIS模型的测试数据结果

Fig. 8 Test data for PSO-ANFIS model

图9 不同模型品位插值结果

Fig. 9 Grade interpolation results of different model

表4 不同模型的RMSE结果

Table 4 RMSE results of different models

3 结论

图10 不同模型的R柱状图

Fig. 10 R histogram of different models

1) 利用粒子群优化算法快速搜索能力，神经网络的学习机制和模糊系统的语言推理能力优势构建PSO-ANFIS品位插值模型，通过学习方式避开繁琐且不易求解的理论分析，有效解决矿体品位变异性强的问题。

2) 利用交叉验证方法选取地质数据库中待估点三维坐标及真实值和其周围8个样品点作为训练数据，运用粒子群优化算法优化品位插值的ANFIS前提参数和结论参数，克服了传统插值方法依靠经验确定参数的局限性，使模型参数的选择更具可靠性。

3) 通过与目标品位及距离幂次反比法品位估值的对比分析，其均方根误差(R)提高了近15%，说明粒子群优化算法(PSO)的自适应模糊神经推理系统(ANFIS)方法进行品位插值具有更好的预测精度和良好的应用前景。

REFERENCES

[1] 崔清松. 空间插值算法在地质建模中的应用[D]. 成都: 西南石油大学, 2010.

CUI Qing-song. Application of spatial interpolation algorithm in geological modeling[D]. Chengdu: Southwest Petroleum University, 2010.

[2] 刘青, 袁玮, 王宝, 彭良振. 基于GA-BP神经网络的金精矿品位的预测[J]. 东北大学学报(自然科学版), 2015, 36(2): 237-240.

LIU Qing, YUAN Wei, WANG Bao, PENG Liang-zhen. Concentrate grade prediction of gold ore based on GA-BP neural network[J]. Journal of Northeastern University(Natural Science), 2015, 36(2): 237-240.

[3] 韩万林, 张幼蒂, 张作祥. 智能化方法在矿石品位估值中的应用[J]. 有色金属(矿山部分), 2000, 52(5): 6-8.

HAN Wan-lin, ZHANG You-di, ZHANG Zuo-xiang. Application of intelligent method in ore grade valuation[J]. Nonferrous Metals(Mining Section), 2000, 52(5): 6-8.

[4] 韩万林, 张幼蒂. 用改进BP算法估算矿石品位[J]. 中国矿业, 2000, 9(3): 83-85.

HAN Wan-lin,ZHANG You-di. Estimation of ore grade by improved BP algorithm[J]. China Mining Magazine, 2000, 9(3): 83-85.

[5] 谭正华, 荆永滨, 王李管, 文中华, 黄俊歆, 陈建宏. 基于空间变异性的IDW矿石品位估值改进方法[J]. 中国矿业大学学报, 2011, 40(6): 928-932.

TAN Zheng-hua, JING Yong-bin, WANG Li-guan, WEN Zhong-hua, HUANG Jun-xin, CHEN Jian-hong. Improved IDW method for ore grade estimation based on spatial variation[J]. Journal of China University of Mining & Technology, 2011, 40(6): 928-932.

[6] 李娟, 李翠平, 李仲学. 基于支持向量回归机的矿体品位插值[J]. 北京科技大学学报, 2009, 31(12): 1498-1502.

LI Juan, LI Cui-ping, LI Zhong-xue. Grade interpolation in orebody based on support vector regression[J]. Journal of University of Science and Technology Beijing, 2009, 31(12): 1498-1502.

[7] 贾明涛, 叶加冕, 寇向宇, 王李管. 品位估值的自适应径向基神经网络构建技术[J]. 煤炭学报, 2010, 35(9): 1524-1530.

JIA Ming-tao, YE Jia-mian, KOU Xiang-yu, WANG Li-guan. The adaptive Radius Basis Function neural network modeling for the deposit grade estimation[J]. Journal of China Coal Society, 2010, 35(9): 1524-1530.

[8] 李翠平, 郑瑶瑕, 张佳, 侯定勇. 基于遗传算法优化的支持向量机品位插值模型[J]. 北京科技大学学报, 2013, 35(7): 837-843.

LI Cui-ping, ZHENG Yao-xia, ZHANG Jia, HOU Ding-yong. Ore grade interpolation model based on support vector machines optimized by genetic algorithms[J]. Journal of University of Science and Technology Beijing, 2013, 35(7): 837-843.

[9] 李翠平, 李仲学, 余东明. 基于泰森多边形法的空间品位插值[J]. 辽宁工程技术大学学报, 2007, 26(4): 488-491.

LI Cui-ping, LI Zhong-xue, YU Dong-ming. Ore grade interpolation based on Thiessen polygon method[J]. Journal of Liaoning Technical University, 2007, 26(4): 488-491.

[10] SHI Xiu-zhi, ZHOU Jian, WU Bang-biao, HUANG Dan, WEI Wei. Support vector machines approach to mean particle size of rock fragmentation due to bench blasting prediction[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(2): 432-441.

[11] ZHOU Jian, LI Xi-bing, SHI Xiu-zhi, WEI Wei, WU Bang-biao. Predicting pillar stability for underground mine using Fisher discriminant analysis and SVM methods[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(12): 2734-2743.

[12] 张玉祥. 小波神经网络遗传算法及其在矿山压力预报中的应用[J]. 中国有色金属学报, 1999, 9(2): 240-244.

ZHANG Yu-xiang. Gentic algorithm of wavelet network and its application in forecasting ground pressure[J]. The Chinese Journal of Nonferrous Metals, 1999, 9(2): 240-244.

[13] 周仲礼, 马腾, 陈秀荣, 秦飞龙. 基于改进RBF的空间插值算法及其在矿体三维可视化中的应用[J]. 成都理工大学学报(自然科学版), 2014, 41(5): 645-650.

ZHOU Zhong-li, MA Teng, CHEN Xiu-rong, QIN Fei-long. Spatial interpoltaion algorithm based on improved RBF and its application to orebody 3D visualization[J]. Journal of Chengdu University of Technology(Science & Technology Edition), 2014, 41(5): 645-650.

[14] SHI Y, EBERHART R C. Empirical study of particle swarm optimization[C]. Proceedings of the 1999 Congress. Washington: DC: IEEE, 1999: 1945-1950.

[15] 崔益安, 李溪阳, 向恩明, 柳建新, 朱肖雄, 纪铜鑫. 基于粒子群优化的双频激电数据联合反演[J]. 中国有色金属学报, 2013, 23(9): 2498-2505.

CUI Yian-an, LI Xi-yang, XIANG En-ming, LIU Jian-xin, ZHOU Xiao-xiong, JI Tong-xin. Joint inversion of dual frequency IP data using PSO[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(9): 2498-2505.

[16] REZAKAZEMI M, DASHTI A, ASGHARI M, SHIRAZIA S. H2-selective mixed matrix membranes modeling using ANFIS, PSO-ANFIS, GA-ANFIS[J]. International Journal of Hydrogen Energy, 2017, 42(22): 15211-15225.

[17] HASANIPANAH M, SHAHNAZAR A, ARAB H, GOLZAR S B, AMIRI M. Developing a new hybrid-AI model to predict blast-induced backbreak[J]. Engineering with Computers, 2017, 33(3): 349-359.

[18] RINI D P, SHAMSUDDIN S M, YUHANIZ S S. Particle swarm optimization for ANFIS interpretability and accuracy[J]. Soft Computing, 2016, 20(1): 1-12.

[19] POUSINHO H M I, MENDES V M F, CATALAO J P S. A hybrid PSO-ANFIS approach for short-term wind power prediction in Portugal[J]. Energy Conversion & Management, 2011, 52(1): 397-402.

[20] LIU P, LENG W, FANG W. Training ANFIS model with an improved quantum-behaved particle swarm optimization algorithm[J]. Mathematical Problems in Engineering, 2013, 2013(1): 78-88.

Grade interpolation of orebody based on particle swarm optimization algorithm and ANFIS

REN Zhu-li^{1, 2}, WANG Li-guan^{1, 2}, JIA Ming-tao^{1, 2}

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;

2. Center of Digital Mine Research, Central South University, Changsha 410083, China)

Abstract: Geological model plays an important role in mineral exploration and development, but in the practice of mine production, because of the influence of cost and technology, it is difficult to obtain the geological data of the whole block, and the spatial interpolation is an important means to solve this problem. The particle swarm optimization (PSO) and adaptive neuro-fuzzy inference system (ANFIS) were applied to the grade interpolation of orebody, which overcomes the limitation of traditional interpolation method based on empirical determination of parameters, PSO-ANFIS grade interpolation model was constructed by using the fast searching ability of particle swarm optimization, the learning mechanism of neural network and the language reasoning ability of fuzzy system. Selecting 571 groups of sample points as training data to train the model with the cross verification method in MATALB, each of these training samples consists of three-dimensional coordinates and true values of the estimated points and eight surrounding sample points, finally, the PSO-ANFIS model was used to evaluate the evaluation point and the mean square root error (RMSE) was improved by comparing with the distance power-time inverse interpolation method, which is nearly 15%. The feasibility and effectiveness of the model were validated.

Key words: ore grade; spatial interpolation; particle swarm optimization algorithm; adaptive neuron-fuzzy inference system; optimization

Foundation item: Project(2017YFC0602905) supported by National Key Research and Development Program

Received date: 2017-11-01; Accepted date: 2018-06-26

Corresponding author: JIA Ming-tao; Tel: +86-13873194121; E-mail: Mingtao_jia@163.com

(编辑李艳红)

基金项目：国家重点研发计划项目(2017YFC0602905)

收稿日期：2017-11-01；修订日期：2018-06-26

通信作者：贾明涛，副教授，博士；电话：13873194121；E-mail：Mingtao_jia@163.com

摘要：地质模型在矿产勘探与开发中具有重要作用，但在矿山生产实践中，由于成本和技术等诸多因素影响，很难获得整个区块的地质数据，而且传统插值方法依靠经验确定参数有很大局限性。提出将粒子群优化算法(PSO)和自适应神经模糊推理系统(ANFIS)应用到矿体品位插值中，利用粒子群优化算法的快速搜索能力，神经网络的学习机制和模糊系统的语言推理能力等优势构建PSO-ANFIS品位插值模型，并借助MATLAB生成571组样本数据作为输入空间对模型进行训练，其中每一个训练样本由待估点三维坐标及真实值和其周围8个样品点组成，最后用训练后的PSO-ANFIS模型对待估点进行品位插值，并与距离幂次反比插值法进行对比，其均方根误差(RMSE)提高了近15%，验证了该模型的可行性和有效性。