J. Cent. South Univ. (2021) 28: 2238-2256
DOI: https://doi.org/10.1007/s11771-021-4765-z
Probabilistic model and analysis of coupled train-ballasted track-subgrade system with uncertain structural parameters
MAO Jian-feng(毛建锋)1, 2, 3, XIAO Yuan-jie(肖源杰)1, 2, 3, YU Zhi-wu(余志武)1, 2, 3Erol TUTUMLUER1, 2, 3, 4, ZHU Zhi-hui(朱志辉)1, 2, 3
1. School of Civil Engineering, Central South University, Changsha 410075, China;
2. National Engineering Laboratory for High-Speed Railway Construction, Changsha 410075, China;
3. Key Laboratory of Engineering Structures of Heavy Haul Railway of Ministry of Education,Central South University, Changsha 410075, China;
4. Department of Civil and Environmental Engineering, University of Illinois at Urbana-Champaign, Urbana,IL 61801, United States
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Abstract:
Random dynamic responses caused by the uncertainty of structural parameters of the coupled train-ballasted track-subgrade system under train loading can pose safety concerns to the train operation. This paper introduced a computational model for analyzing probabilistic dynamic responses of three-dimensional (3D) coupled train-ballasted track-subgrade system (TBTSS), where the coupling effects of uncertain rail irregularities, stiffness and damping properties of ballast and subgrade layers were simultaneously considered. The number theoretical method (NTM) was employed to design discrete points for the multi-dimensional stochastic parameters. The time-histories of stochastic dynamic vibrations of the TBSS with systematically uncertain structural parameters were calculated accurately and efficiently by employing the probability density evolution method (PDEM). The model-predicted results were consistent with those by the Monte Carlo simulation method. A sensitivity study was performed to assess the relative importance of those uncertain structural parameters, based on which a case study was presented to explore the stochastic probability evolution mechanism of such train-ballasted track-subgrade system.
Key words:
Cite this article as:
MAO Jian-feng, XIAO Yuan-jie, YU Zhi-wu, Erol TUTUMLUER, ZHU Zhi-hui. Probabilistic model and analysis of coupled train-ballasted track-subgrade system with uncertain structural parameters [J]. Journal of Central South University, 2021, 28(7): 2238-2256.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-021-4765-z1 Introduction
The dynamic, uneven track settlement caused by the uncertainty associated with the equivalent stiffness and damping properties of the coupled ballast-substructure system has long been the challenging engineering problem adversely affecting railroad operation safety for decades. Such settlement would severe the random track irregularities under the repeated wheel/rail interactions. Therefore, it remains indispensable and critical to efficiently assess the stochastic dynamic responses and performance of the coupled ballast-subgrade system from advanced computational models where the uncertain stiffness and damping properties of the ballast-substructure system, random track irregularities, and their interactions are coupled and properly considered.
The dynamic simulation of the coupled train-ballast-subgrade systems is often indispensable to reveal the dynamic properties of structural components which are triggered by random excitations and parameter uncertainties. For example, the sensitivity and relative importance of system parameters including the car body, rails, ballasted track, subgrade to dynamic responses under random excitations can be obtained through numerical analyses of the coupled train-track model [1]. However, due to the complex nature and multiple sources of such random excitations, the majority of the existing publications were focused on the deterministic analysis with random excitation considered by varying one single factor at a time for simplicity. As one of the most important motivators, the track irregularity has been investigated in many publications. In the last decades, a large number of articles focused on the influence analysis of the track irregularity on the dynamic behaviors of the coupled train-track-substructure systems [2-10]. Furthermore, several researchers paid attention to the studies of random model of track irregularities in contrast to the deterministic analysis. At an early stage, a non-Gaussian model was developed by IYENGAR et al [11] based on the measured irregularities data to simulate the unevenness samples, after which this model is considered a standard way to estimate the expected values on level crossing and peaks [12]. Recently, YU et al [13] developed a nonstationary track irregularity model based on the stochastic harmonic function [14], which is proven to be highly efficient and reasonably effective for the coupled train-ballast-subgrade simulation. XU et al [15, 16] developed a probabilistic model for random track irregularities in the dynamic simulation of the coupled vehicle-track system, which is proven to be effective to better clarify the random vibration characteristics and probabilistic relations between random track irregularities and dynamic behaviors of the vehicle/track system. Also, considerable meaningful work has been done in data mining and stochastic modeling of track irregularities based on experimentally measured data [17-19]. On the other hand, besides the random track irregularity, researchers also focused on the influences of random system parameters involved in the coupled train/track system. The varying material properties and other mechanical uncertainties were investigated for stochastic vibration of the coupled train-ballast-subgrade system based on the perturbation method (PM) with several advanced models, e.g., JIN et al [20], MUSCOLINO et al [21], HUANG et al [22], and CAVDAR et al [23].
In the existing studies, either random track irregularity or uncertainty of system parameters has been well investigated in train-substructure coupled dynamics individually. XIN et al [24] have done well research on the uncertainty and sensitivity analysis for train-ballasted track–bridge system by employing PDEM, in which the material, geometry, structural damping of bridge superstructure and the temporal–spatial ergodic properties of track irregularities are highlighted. WAN et al [25] provided an investigation as to study the uncertainty in the parameter influencing the dynamic responses of time varying time-varying train-track-bridge system, which refers to dynamic sensitivity analysis in the context of stochastic dynamic system. Thus, in reality, these random factors interact with each other and are inseparable in the train-track coupled system. An advanced model, which is able to realistically consider the randomness, complexity and probability of track irregularities and system parameters, needs to be developed to fully characterize stochastic dynamic responses of the train-ballast-subgrade system so that the railway system performance and safety can be maintained or improved.
The aim of this paper was to develop a probabilistic model of the coupled train-ballast track-subgrade system (TBTSS) for estimating the stochastic dynamic interactions between ballast and subgrade, where the coupling effect of track irregularities and the uncertainty of structural parameters of the coupled ballast-subgrade system was considered. The multi-dimensional system parameters were generated by the discrete points design method termed as the number theoretical method (NTM) [26] in hypercube space. The time histories of dynamic vibrations of TBSS under stochastic excitations including the uncertainty of system parameters (e.g., equivalent stiffness and damping of rail pad and equivalent stiffness and damping of the ballast-subgrade system) were computed accurately with high efficiency based on the probability density evolution method (PDEM) [27, 28]. Results from numerical simulations and relevant sensitivity study on the TBSS model based on PDEM were presented and verified against those by the Monte Carlo method (MCM). Finally, a series of time-space stochastic dynamic responses were explored with significant conclusions drawn.
2 Stochastic model of coupled train-ballast-subgrade system
Apart from random track irregularities and certain other stochastic excitations, the stochastic dynamic responses of the coupled train-ballast-subgrade system are influenced by parameter uncertainties as well, e.g., stiffness uncertainties of the ballast-substructure system, and damping uncertainties of the subgrade system [29]. For example, the ballast equivalent stiffness kb is ranged from 165 to 220 MN/m, and the subgrade equivalent stiffness ks is ranged from 40 to 133 MN/m. As evident from such wide ranges, the uncertainty of those values is so great that they cannot be neglected in the dynamic simulation. Therefore, the influence of stochastic parameters of the ballast-subgrade system on the dynamic responses of the train-ballast-subgrade system was investigated in this study.
2.1 Model assumptions
1) The train runs on the track at a constant speed. The wheel sets remain full contact with the rail surface, and there is no sliding, climbing derailment, or jumping derailment.
2) The vehicle bodies, bogies, and wheel sets are assumed as rigid bodies, and no eccentricity of vehicle gravity occurs. The stiffness and damping properties of the vehicle spring between the first and second suspensions are linear.
3) The coupled ballast-subgrade system is assumed to be a conservative system, which means that any inflow probability in the state space domain is exactly equal to the outflow probability transited through the boundary domain [30].
4) To highlight the impact of stochastic system parameters, only one representative track irregularity sample was used as the wheel/rail excitation in the simulation.
2.2 Stochastic dynamic equation of coupled train-ballast-subgrade system
In this paper, a typical coupled ballast-subgrade system was established. As shown in Figure 1, the stochastic dynamic behavior of the coupled train-ballast-subgrade system is a complex time-varying dynamic process under the vehicular loading, where the uncertainties of the ballast-subgrade system parameters should be considered. This section presents the numerical framework of modelling the coupled train-ballast-subgrade system.
2.2.1 Equations of vehicle model and its wheel/rail interaction
As shown in Figure 1, the coupled ballast-subgrade system involving random parameters was modeled as an elastic dynamic system. It was established with the invariant principle of total potential energy [31], based on which a vehicle model was also established (as shown in Figure 2).
The train consists of two locomotives at both ends, between which are the Nv-2 passenger cars. Each of the vehicles consists of one car body, two bogies, four wheel-pairs and the spring-damper connections between the first and second suspensions [32]. Each car body and bogie has six degrees of freedom (DoF), which are respectively designated by the longitudinal displacements xci and xtji, lateral displacements yci and ytji, vertical displacements xci and ztji, roll displacements θci and θtji, yaw displacements ψci and ψtji, and pitch displacements φci and φtji. Each wheel-set has five DOFs, including longitudinal displacement xwki, lateral displacement ywki, vertical displacement zwki, roll displacement θwki, and yaw displacement ψwki, where j=1, 2 and k=1, 2, 3, 4 in the ith vehicle. The subscripts “c”, “t1”, “t2” and “w” denote the vehicle body, front bogie, rear bogie, and wheel-pair. In total, the vehicle model used in this paper has 38 DoFs, of which the suspension connections between the car body and bogies and between the bogies and wheel-sets are represented using linear springs and viscous dashpots.
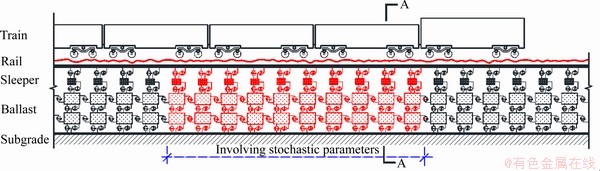
Figure 1 Stochastic model of coupled train-ballast-subgrade system
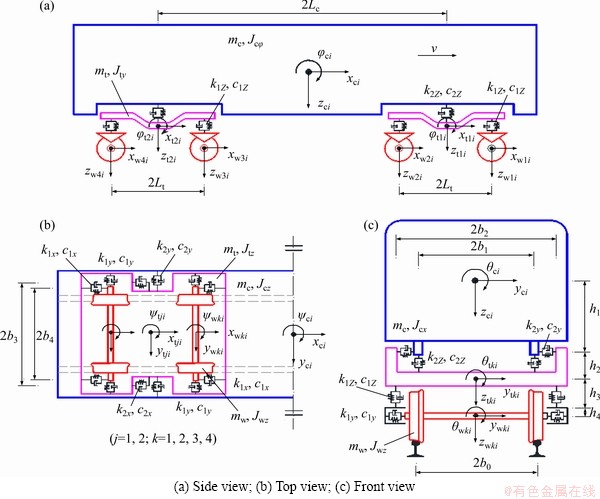
Figure 2 Three-dimensional vehicle model involving random parameters:
Considering the excitations of wheel/rail interaction, the vehicle dynamic equation can be expressed as follows:
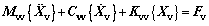(1)
where Mvv, Cvv and Kvv denote the mass, damping and stiffness matrices of the vehicle, respectively; {Xv} is the corresponding displacement vector; Fv is the force vector generated from the wheel/rail interactions including the excitation of track irregularities. The details on forming these matrices can be referred to Ref. [32].
As shown in the 3D wheel/rail contact model [33] in Figure 3, the wheel/rail interaction consists of contact forces formulated by the Hertz theory of normal elastic contact for a normal plane [34] and the Kalker linear rolling contact theory in the tangential plane [35], of which the detailed information can be referred to Refs. [36, 37].
The wheel/rail creep forces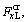 
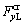and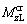 
on the left wheel and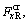 
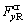and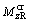 
on the right wheel can be calculated using the Kalker linear creep theory. Specifically, the wheel/rail creep forces can be written as:
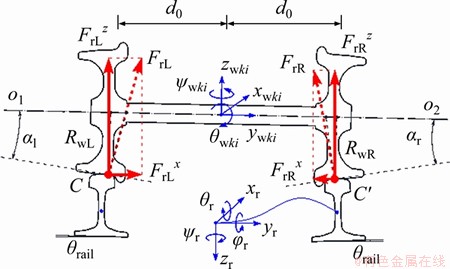
Figure 3 Wheel/rail interaction model used in coupled train-ballast-subgrade system
(2)
where 
and 
(m=11, 22, 23, 33) denote the creep coefficients between the kth wheel set and the left and right rail in the ith vehicle, respectively, which can be obtained according to Ref. [37]; and
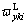and
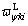denote respectively the longitudinal wheel/rail creepage, lateral wheel/rail creepage and spin wheel/rail creepage between the kth wheel-set and the left rail in the ith vehicle, whereas 
, 
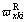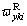and 
are for the right rail.
2.2.2 Equations of coupled ballast-subgrade model
The cross-section A-A of the coupled ballast-subgrade system subjected to the vehicle load in Figure 1 is shown in Figure 3. As mentioned before, the uncertainty of the ballast-subgrade system parameters is considered to be the only stochastic source in the ballast-subgrade model. The six different types of parameters are independently assumed to be normally distributed, but non-independent and related to each other for the sub-parameters in each type of parameters.
Without loss of generality, set symbol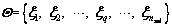 
as the vector space of the random parameters in the ballast-subgrade coupled system. The subvector 
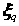can be written as
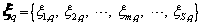
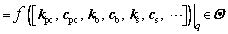(3)
where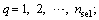 
f(·) is the transfer function
of the vector of stochastic parameters;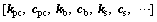
is the vector of stochastic target parameters that are of interest in the model, e.g., the equivalent stiffness kpc and equivalent damping cpc of rail pads and fasteners, the equivalent stiffness kb and equivalent damping cb of ballast, the equivalent stiffness ks and equivalent damping cs of subgrade; nsel is the total number of representative discrete point sets; S is the number of random variables.
Taking the major parameters of ballast-substructure system as an example, if there are only six types of parameters considered in the calculation, e.g. the equivalent stiffness and damping parameters presented in the random variable vector in Eq. (3), it is rewritten as:
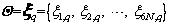
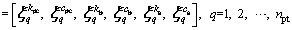(4)
where the submatrices in state space Θ are represented as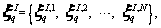 
I=kpc, cpc, kb, cb, ks and cs, of which the details on forming the discrete variables are presented in the following sections.
In order to better illustrate the physical model in Eq. (4), the close-up view of a specific portion of the ballast-subgrade structures in Figures 1 and 4 is provided as follows.
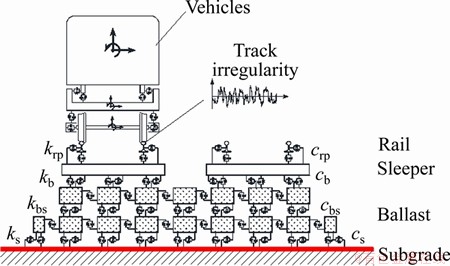
Figure 4 Ballast-subgrade coupled system involving stochastic system parameters
The ballast-subgrade structure shown in Figure 3 was modeled using discrete lumped mass blocks connected by a series of springs and dampers. The rails were simulated with finite element method as uniform Bernoulli-Euler beams and the sleepers were regarded as rigid beams. The track foundation and subgrade soil were treated as linear elastic. Considering the stochastic parameters of the ballast-subgrade system that are consistently involved in the random variable space Θ, the general form of the motion equation is expressed as follows:
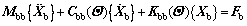(5)
where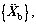 
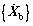and 
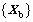denote the acceleration, velocity and displacement vectors of the ballast-subgrade structure; Mbb, Kbb(Θ) and Cbb(Θ) denote the mass matrix, stochastic equivalent stiffness matrix and stochastic equivalent damping matrix, which represents the randomness of ballast-subgrade system parameters involved in the parameter space Θ; Fb denotes the force vector acting onto the coupled ballast-subgrade system that involves the excitations of track irregularities and vehicle loads.
Due to the flexibility of the ballast and subgrade foundation, each of these mass blocks in Figure 4 was allowed to move longitudinally (x direction), vertically (y direction) and laterally (z direction), but the rotation of each axis was ignored. The two rails of track have six DoFs and are connected to the sleepers which are assumed as rigid elements. Therefore, the mass matrix Mbb can be written as:
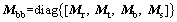(6)
where Mr, Mt, Mb and Ms denote the mass submatrices of rails, sleepers, ballast and subgrade that are divided into blocks, respectively.
On the basis of stochastic model in Figure 5, since there exists the only stochastic parameter presented in Eq. (4), the stochastic equivalent stiffness matrix in Eq. (5) can be written as:
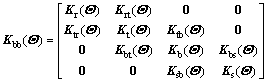(7)
where Kr(Θ) and Kt(Θ) are the equivalent stiffness matrices of rail elements and concrete sleepers, respectively;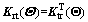 
and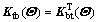 
are the equivalent interaction stiffness matrices between rails and concrete sleepers, the concrete sleepers and upper surface boundary of ballast, respectively; 
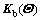and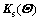 
are the stochastic equivalent stiffness matrices of ballast and subgrade involving random parameters, respectively; 
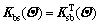is the equivalent interaction stiffness matrix between the ballast and subgrade, respectively; superscript T denotes the transposed matrix.
The equivalent damping matrix Cbb(Θ) in Eq. (5) has the same form as the equivalent stiffness matrix Kbb(Θ), i.e., it just needs to replace the equivalent stiffness symbol K in Eq. (7) with the equivalent damping symbol C.
The load vector Fb which includes the direct influence of track irregularity is written as:
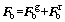(8)
where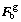 
is the dead axle load vector transferred from vehicle, 
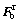is the force vector induced by the wheel/rail interaction and includes the excitation of track irregularity. More details on forming these matrices are presented elsewhere [32].
2.2.3 Dynamic equation of coupled train-ballast-subgrade system
Combining Eq. (1) and Eq. (5) with the given wheel-rail interaction, the stochastic dynamic equation of the coupled ballast-subgrade system can be established as:
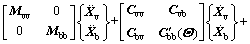
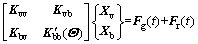(9)
where Mbb, Cbb(Θ) and K′bb(Θ) are the mass, stochastic equivalent damping, and stochastic equivalent stiffness matrices associated with the coupled rail-ballast-subgrade system involving stochastic parameters, as well as the contribution from the wheel/rail interaction force of the vehicle’s wheel pairs; 
and 
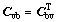are the equivalent stiffness and equivalent damping matrices representing the wheel/rail interactions; the matrices 
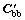and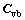 
have the same form as 
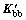and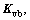 
so one can obtain the matrices 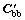and 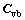by simply replacing K with C and k with c; Fg(t) represents the deterministic excitation vector due to the gravity acting on the vehicles; Fr(t) represents the excitations that due to the track irregularities acting on the ballast-subgrade system. For greater clarity and convenience, by using the principle of superposition, the stochastic dynamic equation in Eq. (9) can be rewritten as:
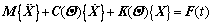(10)
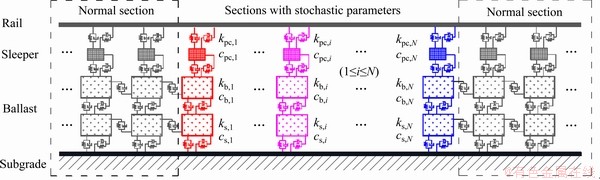
Figure 5 Partially enlarged model of coupled ballast-subgrade system with stochastic parameters
2.3 Point design of stochastic parameters
As the stochastic dynamic equation of ballast-subgrade coupled system involving random systemically parameters established in Eq. (10), the probability density evolution method (PDEM) [27, 28] is employed to solve the stochastic problem. PDEM is a newly developed method that is used to capture the probabilistic properties of stochastic processes, especially the probability density function (PDF) of linear or nonlinear dynamic systems through the stochastic dynamic responses. On this basis, some effective uniform points set of stochastic parameters mentioned in Eq. (10) should be elaborately designed for the better calculation by PDEM.
It is worth noting that each parameter might not have the same target probability distribution function due to material property differences, which may result in the multi-dimensional point design with different probability distributions. The traditional uniform design methods, i.e., the good point (gp) method and the good lattice point (glp) method [38], are developed for uniform designs with multidimensional parameters and collectively known as number theoretical method (NTM) for point design. Meanwhile, continual further investigations also are extended on uniform designs with large-size variables [39, 40]. Here, an approach named as “Number theoretic method of multi-target probability distribution” (NTM-mp) [32] which developed based on NTM is employed for the point design of stochastic parameters in TBSS.
As the random vector point set
q=1, 2, …,npt) mentioned in Section 2.2 is combined with the sub-vector point set of stochastic parameters of equivalent stiffness and damping of rail-ballast-subgrade coupled system, these parameters are independently assumed to be normal distribution for the different structure layer, but non-independent and related to each other in the same layer. The correlation between the parameters is non-uniform, which means a closer distance between two parameters, indicating a larger correlation between them. Therefore, the correlation coefficients [41] can be assumed to be:
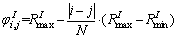
with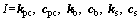 
(11)
where i and j are the numbers of rows and columns in correlation coefficient matrix, and i=1, 2, …, N, j=1, 2, …, N;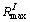 
and 
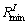are the maximum and minimum correlation coefficient, respectively. N is the total number of random variables in each kind of parameters, such as the ballast equivalent stiffness Kb.
Therefore, referring to Ref. [42], the correlation coefficient matrix of random variables in the state space Θ that obey the normal distribution in 6N dimensions can be derived by:
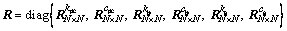(12)
where the submatrix of correlation coefficient is written as:
with 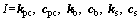(13)
Using the Cholesky decomposition on account of its symmetries and positive definiteness, the upper triangular matrix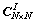 
of correlation coefficient matrix 
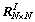can be obtained 
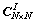with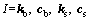 
. On this basis, the total upper triangular matrix of correlation coefficient matrix in Eq. (12) is derived as:
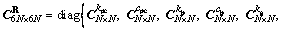
(14)
Return to the initial status in Eq. (4), without loss of generality, as the number theoretic method of multi-target probability distribution (NTM-mp) mentioned in Ref. [32], and assume that there exists a vector Ps in the s-dimensional hypercube 
which follows:
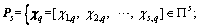
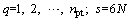(15)
where the point set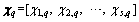
in hypercube space
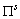can be well designed using traditional number theory.
Herein, the discrete point set in s-dimensional hypercube in Eq. (15) is designed by the gp method which is mentioned in the number theoretical method (NTM) [38]. The evenly scattered point set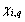 
is derived as:
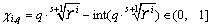
(16)
where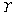
denotes a prime number.
As the random variable 
q=1, 2, …, npt is assumed to be non-uniform probability distributions, the inverse transformation of probability function distribution [38] is employed to transform the uniform designed discrete points of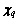 
into non-uniform designed discrete points 
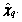Here, each random variable is assumed to be normal distribution functions. There exists:
(17)
where i=1, 2, …, 6N; q=1, 2, …, npt;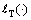 
is the Rosenblatt transformation function;
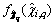is the target normal probability density function; 
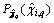denotes the probability distribution function.
On this basis, considering the correlation coefficient matrix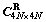 
in Eq. (14), the final designed discrete point set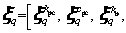 
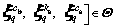can be constructed as follows:
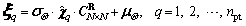(18)
In this case, the discrete point set of multi-dimensional random parameters with target probability density functions is designed. The total probability satisfies:
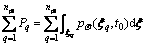
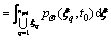
(19)
where Pq is the initial probability of each designed point set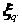 
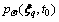denotes the joint probability density function, and the initial conditions of each design point set are partially discretized correspondingly as follows:
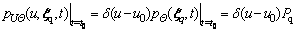(20)
where δ(·) is the Dirac delta function.
2.4 Solution with PDEM
The ballast-subgrade coupled system is a conservative system which means that the total probability of the systems is equal whenever the probability is inflow or outflow in any domain of the state space. With the initial conditions given above, the randomness of dynamic equation of ballast-subgrade coupled system is from the stochastic parameters set Θ and the solution is real and unique [44].
The steps for calculation of ballast-subgrade coupled system with PDEM are shown as follows:
1) After the numerical point design above, the representative points set ξq in the random systemically parameters space Θ with the initial probability Pq is obtained.
2) Considering the stochastic parameters in Eq. (4), the stochastic dynamic responses of ballast-subgrade coupled system in Eq. (10) with the deterministic analysis with the Newmark-β integration method step, for more general form, the stochastic dynamic response vector can be derived as:
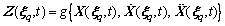(21)
where g{·} denotes the conversion function, and
denotes the vector involving the stochastic dynamic responses interested, of which the velocity is 
.
3) With the initial condition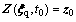
, the ballast-subgrade coupled system is considered the probability conservation system. Based on the Reynold transform theorem and its relevant derivation, the stochastic response 
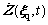obtained in Step 2) is presented into the discretized version of PDEM [45], the probability density evolution equation writes:
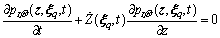(22)
The initial condition 
is given when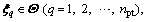
the initial probability of Eq. (22) is determined by:
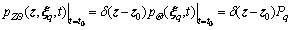(23)
4) Then, the stochastic dynamic equation can be solved with the finite element method of bilateral difference method and the total variation diminishing (TVD) scheme [28]. In this step, the response space-time (z, t) in probability function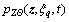 
should be meshed, and the nodes denoted as (zi, tk),i=0, ±1, ±2, …,k=0, 1, 2, …,, where 
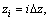tk=k△t, △z is the space step in the direction of z and △t is the time step.
5) Finally, synthesize the results in Step 4), and then the instantaneous probability density function through the discretized probability values is shown as:
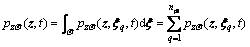(24)
The calculation frame chart of train-ballast-subgrade coupled system is shown in Figure 6, and for more details of the derivation process of PDEM can refer to Ref. [28].
3 Model verification and case studies
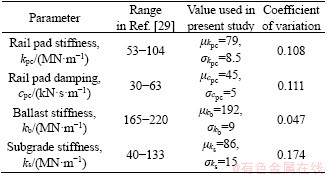
A ballast-subgrade coupled model featuring four sections of rail-sleeper-ballast-subgrade sub-models involving stochastic parameters is established in Figure 7, where the ballast-subgrade structure is divided into four sections with each 15 m length in the middle and two sections at each end with infinite length. The mass blocks of ballast and subgrade are divided by Lx=0.615 m in the longitudinal direction and Ly=0.80 m in the lateral direction. The ballast thickness is Hb=0.5 m, and the subgrade thickness is Hs=1.5 m with the slope angle α=35°. The major parameters in the middle four sections considered the stochastic parameters are shown in Table 1, and the major data are referred from Ref. [29], e.g., the stiffness and rail pad damping with fastener, ballast and subgrade are distributed within random ranges. Assume that all of random parameters used in the present paper satisfy the normal distributions.
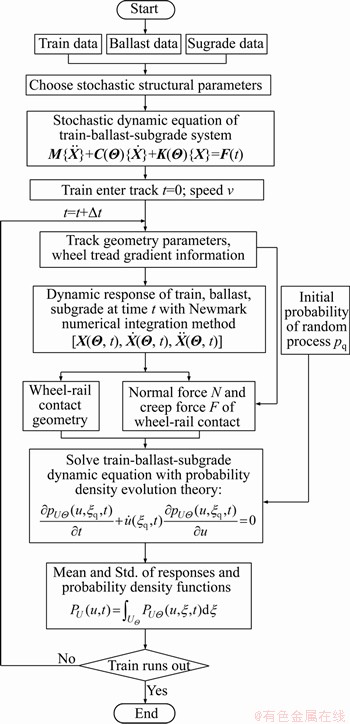
Figure 6 Calculation frame chart of train-ballast-subgrade coupled system
The train model contains eight vehicles, with four motor cars and four trailer cars as the marshalling. The major parameters of the vehicles are listed in Table A-1 in Appendix. The train is assumed to run along the ballast-subgrade system with a constant velocity of 250 km/h. Although the track irregularities are normally considered the random excitations in many prevent studies, only a determined track irregularity sample at each position is considered, e.g., the vertical track irregularity sample shown in Figure 8. The track irregularity samples used as the wheel/rail excitation are generated by German low-interference track spectrum, whose cut-off spatial frequency ranges from 0.04 to 3.14 rad/m.
Figure 7 Ballast-subgrade coupled model with stochastic parameters in numerical study
Table 1 Value range of parameters used in ballast-subgrade coupled system
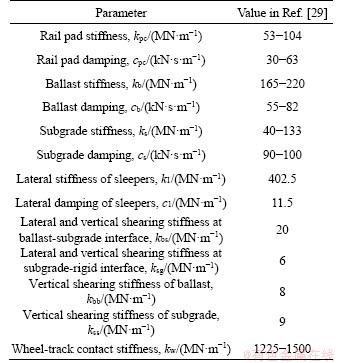
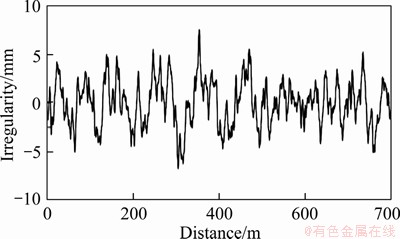
Figure 8 Vertical track irregularity sample used on left rail
3.1 Numerical verification
As mentioned in many publications, the Monte Carlo method (MCM) was normally used for the verification of other new random theories for its efficiency at an acceptable calculation precision. The mean values (Mean) and the standard deviation values (Std) are frequently used.
In order to reduce the computational cost of large amount calculation of MCM, the number of vehicles used in the train model is reduced to one motor car and one trailer car. Only one stochastic parameter is considered in the verification model, which is the random rail pad stiffness. The random rail pad stiffness krp is assumed as normal distribution, with the mean value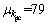 
MN/m and the standard deviation value 
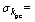8.5 MN/m. The train speed is 250 km/h.
On the basis of the track irregularity samples and the track-subgrade model mentioned in Section 3.1, the calculations are carried out using PDEM and MCM. According to the curves shown in Figure 9, the results obtained by PDEM coincide well with the ones obtained by MCM, where only 400-representative-points design is used in the the probability density evolution method (PDEM) calculation while MCM uses as many as 9999 samples. In details, the maximum deviation between the random responses obtained by PDEM and MCM is less than 1.0 %. Obsoletely, PDEM shows a higher efficiency at the same calculation precision when compared to MCM.
3.2 Sensitivity analysis of structural parameters based on the deterministic model
As the data shown in Table 1, there are several major stochastic parameters referred to Ref. [26], e.g. the rail pad stiffness ranges from 53 to 104 MN/m while the stiffness of subgrade ranges from 40 to 133 MN/m. With such huge uncertainty on these parameters, it is hard to point out which one is the most important just through defining their value ranges. The sensitivity analysis on these structural parameters is extremely needed.
The sensitivity analysis of stochastic parameters is designed through several simple numerical calculations. On the basis of the stochastic model of train-ballast-subgrade coupled system established the sections before, all the stochastic parameters are defined as the deterministic ones. Taking the rail pad stiffness which ranges from 53 to 104 MN/m as an example, the data ranges are divided into 13 equal parts from 53 to 104 MN/m, named S1 to S13 with the values gradually increasing. The same rules with the other stochastic parameters are listed in Table 1. The major stochastic parameters in the sensitivity analysis are the rail pad stiffness kpc and damping cpc, the ballast stiffness kb and damping cb, the subgrade stiffness ks and damping cs. When considering the uncertainty of a special parameter in the numerical case studies, the values of other ones are determined using the middle values in the case of S7. Therefore, there are totally 6×13=78 calculation cases in the sensitivity analysis. All case studies present in the sensitivity analysis use the same track irregularity samples mentioned in Section 3.1.
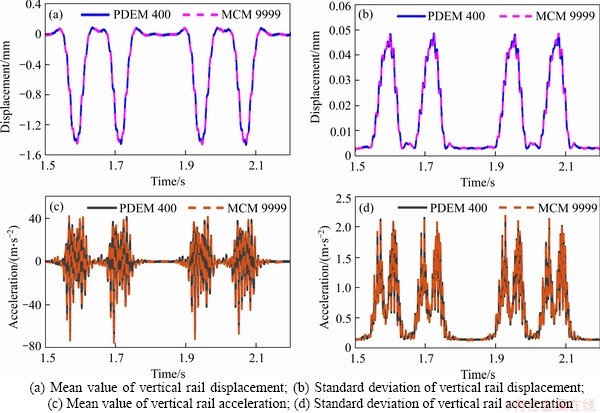
Figure 9 Verification of results got by PDEM and MCM:(v=250 km/h)
As one of the most important responses that directly act on the running safety of wheel/rail interaction, the rail deformations under vehicle loading normally attract attentions. The sensitivity analysis of the systematically stochastic parameters on rail displacement at the position of rail pad is shown in Figure 10. The rail displacement curves at rail pad distributed on a huge range and showing great uncertainty at a total number of 78 numerical case studies under the influence of uncertain parameters. This shows that the influence of randomness of parameters on rail vibration responses can not be ignored.
Calculating the minimum value (maximum in absolute values) of the rail displacement curves at different cases, one can plot the minimum data with the cases from S1 to S13 by different kinds of parameters in Figure 10(c). The value of the case S7 is considered the standard value at each parameter analysis case. The increment or decrement (△) of the response value can be calculated by
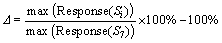(25)
where i=1, 2, …, 13; max(Response(Si)) presents the maximum absolute value of response in the case ‘Si’.
As shown in Figure 10(c), these lines have mostly continuous decreasing trend, and the ranges are comparatively large for the lines of the stiffness of rail pad krp, ballast kb and subgrade ks. Especially, for the subgrade stiffness ks, the maximum values of rail displacement in the vertical position do not decrease in linearity when the subgrade stiffness is increasing. Actually, the stiffness of subgrade has a huge impact on the rail displacement, especially at the S1 case (ks=40 MN/m) the maximum extremum displacement increased by 48% while at the S13 case (ks=133 MN/m) the maximum extremum displacement decreased only by 12%. Compared with the sensitivity analysis of other stochastic parameters in the present study, the most important parameters should be considered their uncertainty, in turn the stiffness of subgrade, the stiffness of rail pad and then the stiffness of ballast. As for the rail displacement, the damping uncertainty of ballast-subgrade system may be ignored due to the negligible effects acting on the responses, the difference of which is even less than 0.05%, referring to the local magnified drawing in Figure 10(c).
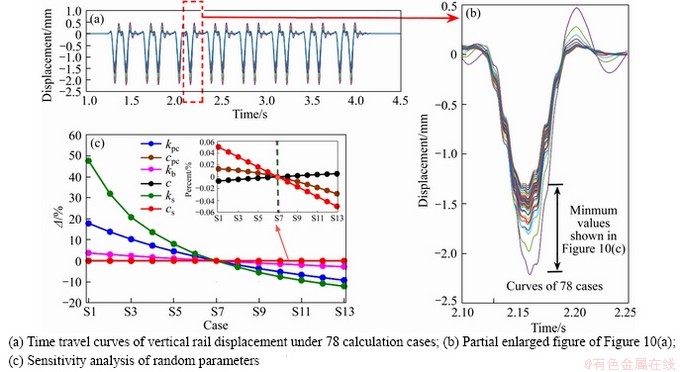
Figure 10 Sensitivity analysis of systematically stochastic parameters on rail displacement at position of rail pad:(v=250 km/h)
To further fully validate the results in Figure 10, the accelerations of each typical structure of full train-ballast-subgrade coupled system are shown in Figure 11. The acceleration of each substructure is obviously influenced by the stiffness of subgrade, then the stiffness of rail pad, and the third one is the stiffness of ballast. The accelerations decreased with the increase of stiffness and damping in linearity or small nonlinearity. The stiffness of subgrade is always one of the most important factors that should be seriously considered. The trend curves of maximum responses values drawn in Figure 11 show that enhancing the subgrade and improving its stiffness in the extend permit will greatly reduce the vibration amplitude.
It is worth mentioning that, referring to Figure 11(a), the systematically structural parameter uncertainty does not so greatly impact the vehicle acceleration maybe because the amplitude change of rail displacement is not so large, compared to the amplitude of track irregularity samples. In Figure 11(b), the rail pad damping is also a great important factor that should not be ignored for the rail accelerations control. The greater the damping of rail pad, the smaller the acceleration of rail element. In the opposite, increasing the stiffness of rail pad and ballast, the accelerations of the ballast and subgrade will increase, which will also make disadvantages for the ballast-subgrade interaction.
Totally, in order to get better control of structural responses of train-ballast-subgrade coupled model established in the present paper, the stiffness uncertainty of subgrade, rail pad and ballast, as well as the damping uncertainty of rail pad, should be considered. Meanwhile, the uncertainty of ballast damping and subgrade damping may be ignored due to its insensitivity.
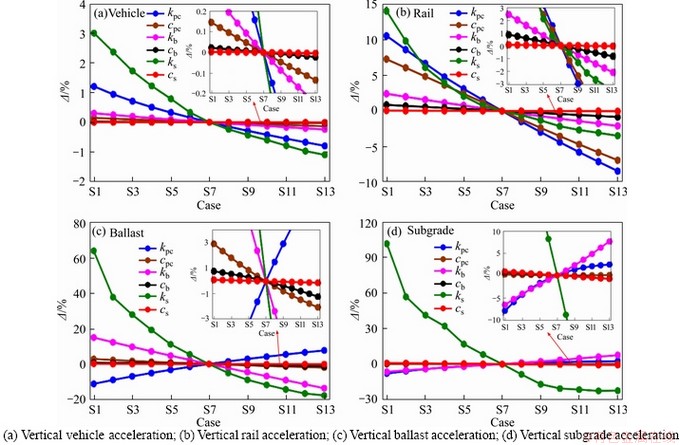
Figure 11 Sensitivity analysis of systematically random parameters on different dynamic responses:(v=250 km/h)
3.3 Case studies and probability interval estimation
Except for the excitations of random track irregularities, how great the stochastic systematically structural parameters will affect the dynamic responses needs investigation. The stochastic systematically structural parameters used in the present case study are shown in Table 2, where μ denotes the mean value and σ denotes the standard deviation value.
3.3.1 Probability interval estimation of random responses
Based on the train-ballast-subgrade coupled model established in the present paper, combining the randomness of the major structural parameters such as the stiffness of subgrade ks, rail pad kpc and ballast kb, the damping of rail pad cpc synchronously,the point set of stochastic parameters in Eq. (4) can be reconstructed as:
q=1, 2, npt (26)
All of the stochastic parameters are assumed to be normal distribution functions. The maximum and minimum correlation coefficients of the variables in Eq. (26) are assumed as 0.6 and 0.0. The stochastic parameters for the rail-ballast-subgrade models are listed in Table 1, and the vehicle parameters are listed in Appendix I.
Table 2 Stochastic systematically structural parameters
Deriving Eq. (26) into the dynamic equation of Eq. (10) and solving the investigative procedures following the illustration in Figure 6, one can get the probability density function of random responses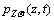
. Therefore, there is
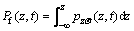(27)
where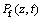 
is the cumulative distribution function and satisfies 
.
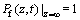The time-history expectation values of random responses Ez(t) can be calculated by
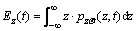(28)
It is convenient to get the dynamic indices of probability extreme estimation that evolve over time-history procedures. Define the time-history dynamic probability values of interval estimation with lower and upper limit values at specified probability value as zl(t) and zu(t), respectively. If the given confidence probability is ptarget, it satisfies
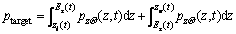(29)
where the sub-equations in Eq. (29) also satisfy
(30)
Therefore, the interval estimation with upper limit value zl(t) and lower limit values zu(t) can be calculated by
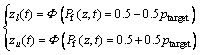(31)
where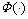
denotes the inverse function of cumulative distribution function.
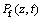3.3.2 Dynamic analysis of random responses
With the same track irregularity samples acting on former cases, the same typically results of random responses are shown as follows.
As a schematic diagram, the three-dimensional time-history probability density function (3D PDF) of the vertical vehicle acceleration when the train speed is 250 km/h is shown in Figure 12, where the mountain-resembled time-history processes of PDF fully demonstrate the random dynamic characteristics of vehicle acceleration.
Taking the vehicle response as an example, the random displacement and random acceleration of car-body in the vertical position are plotted in Figure 13. The probability contours of vertical vehicle acceleration in Figure 13(d) are drawn from 3D probability density functions in Figure 12.
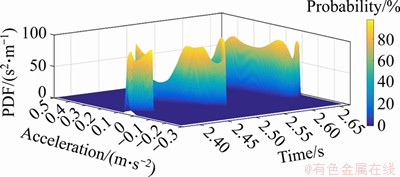
Figure 12 3D probability density functions (PDF) of vertical vehicle acceleration (v=250 km/h)
As shown in Figure 13(a) and the partial enlarged plot in Figure 13(b), the vertical displacement of car-body at the gravity center distributed in a range from -6.62 to -7.35 mm at the local peak, of which the expectation value at the peak is -6.99 mm and a huge difference reaches to 0.73 mm between the two limit values. Therefore, the possible vehicle displacement under the influence of the systematically structural parameters randomness maybe increased by 4.86% or decreased by 5.29%. The phenomenon clearly defines the interval of PDF contours in Figure 13(b), where the time-history interval estimations with lower values zl(t) and upper values zu(t) at a confidence probability ptarget=99.74% are well coincided. Using the similar analysis ideas, the vertical accelerations of car-body at the gravity center distributed in a range from 0.34 to 0.48 m/s2 at the local peak, with the expectation value 0.39 m/s2. The possible vehicle acceleration under the influence of the systematically structural parameters randomness maybe increased by 12.82% or decreased by 23.08%. Therefore, it is clear that the randomness of systematically structural parameters considered in Table 2 has the unnegligible effect on the vehicle’ random dynamic responses.
The smoothness of rail surface is one of the most important factors that will greatly influence the railway running safety. Except for the track irregularity existing on the rail, the dynamic rail deformation randomness that occurs under vehicle loading due to the substructural stiffness and damping uncertainty is also extremely important.
Similar with the plots in Figure 13, the random rail responses (displacement and acceleration) of rail element at the rail pad in the vertical position are shown in Figure 14, where the possible time-history interval estimation is calculated by the probability density functions. From the subfigures in Figure 14, one can clearly know that the vertical displacement of rail element at the rail pad is distributed in a range from -1.29 to -2.01 mm at peak with the expectation value at -1.56 mm. A huge difference between the two limit values reaches to 0.72 mm, which means the possible rail displacement under the influence of the systematically structural parameters randomness maybe increased by 28.84% or decreased by 17.31%. Similar results are got from the random rail acceleration in Figures 14(c) and (d).
It is worth noting that the difference of vehicle displacement between the upper and lower limit values at the peak in Figure 13(b) is 0.73 mm while the difference of rail displacement at peak in Figure 14(b) is 0.72 mm, under the influence of systematically structural parameters uncertainty. This phenomenon confirms the coupled vibration between the train and rail-ballast-subgrade system and the train can be directly deformed by the rail deformation caused by the systematically structural parameters uncertainty.
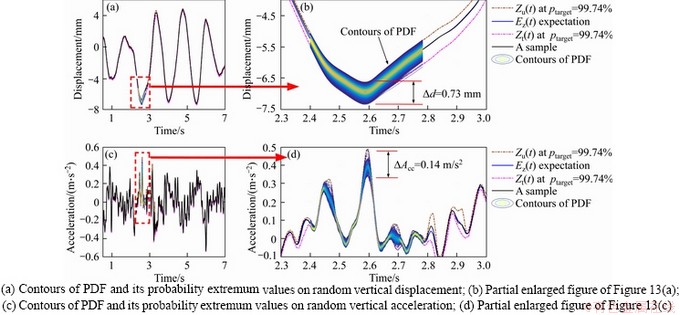
Figure 13 Random dynamic responses of car-body at gravity center:
Figure 14 Random dynamic responses of rail at rail pad:
Combined with the sensitivity results got in Section 3.2, the results discussed are strong to support the opinion that the change of the stiffness and damping of ballast-subgrade system due to the systematically structural parameter uncertainty will greatly influence the dynamic rail deformation, and directly influence the railway running stability and safety. When designing the rail-ballast-subgrade system, the uncertainty of systematically structural parameters, such as the stiffness of subgrade, rail pad, ballast and the damping of rail pad, needs to be priorly considered, especially the stiffness of subgrade and rail pad.
4 Conclusions
A computational probabilistic dynamic model of 3D train-ballast track-subgrade coupled system (TBTSS) for the stochastic dynamic estimation of train-ballast-subgrade interaction is established, where the coupling effect of track irregularities, the stiffness and damping uncertainty of ballast-subgrade system are simultaneously considered. Number theoretical method was employed to the discrete multidimensional parameters points design. Several cases and sensitivity analysis are presented for detailed numerical investigation.
1) Compared with MCM, the time-varying stochastic dynamic vibrations of train-ballast-subgrade coupled system under systematically structural parameters uncertainty can be solved accurately with high efficiency by employing the probability density evolution method.
2) With a series of parameter sensitivity analysis, the results show that the uncertainty of subgrade stiffness, rail pad stiffness, ballast stiffness and rail pad damping needs to be priorly considered in the railway design. Meanwhile, the uncertainty of ballast damping and subgrade damping is insensitive in the present study.
3) The systematically structural parameter uncertainty of rail-ballast-subgrade system will greatly influence the dynamic rail deformation, and directly influence the railway running stability and safety.
4) Using the present probabilistic model established in the paper, the stochastic probability evolutionary interval estimation of random dynamic responses can be accurately estimated at the given confidence probability.
Contributors
The overarching research goals were developed by MAO Jian-feng and XIAO Yuan-jie, and they established the models, calculated the results and edited the draft of manuscript. YU Zhi-wu and Erol TUTUMLUER provided the concept of manuscript and improved the quality of manuscript. ZHU Zhi-hui helpd to establish the model and verified the calculation. All the authors replied to reviewers’ comments and revised the final version.
Conflict of interest
MAO Jian-feng, XIAO Yuan-jie, YU Zhi-wu, Erol TUTUMLUER and ZHU Zhi-hui declared that they have no conflicts of interest to this work.
Appendix
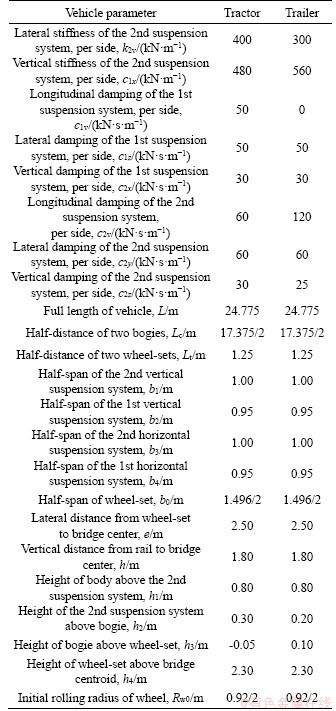
Table A-1 Major parameters of vehicle used in this study
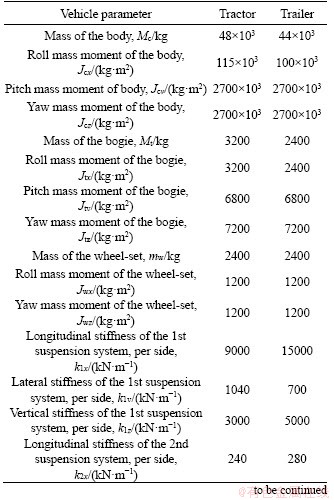
Continued
References
[1] ZHAI Wan-ming, XIA He, CAI Cheng-biao, GAO Mang-mang, LI Xiao-zhen, GUO Xiang-rong, ZHANG Nan, WANG Kai-yun. High-speed train-track-bridge dynamic interactions-part I: Theoretical model and numerical simulation [J]. International Journal of Rail Transportation, 2013, 1: 1-24. DOI: 10.1080/23248378.2013.791498.
[2] ZHAI Wan-ming. Vehicle-track coupling dynamics (fourth edition) [M]. Beijing, China: Science Press, 2015. (in Chinese)
[3] SUN Y Q, DHANASEKAR M D. A three-dimensional model for the lateral and vertical dynamics of wagon-track systems [J]. Journal of Rail & Rapid Transit, 2003, 217(1): 31-45. DOI:10.1243/095440903762727339.
[4] ZAKERI J, XIA He, FAN Jun-jie. Dynamic responses of train-track system to single rail irregularity [J]. Latin American Journal of Solids & Structures, 2009, 6 (2): 89-104. DOI: 10.1243/095440903762727339.
[5] KARDAS-CINAL E. Spectral distribution of derailment coefficient in non-linear model of railway vehicle-track system with random track irregularities [J]. Nonlinear Dynamics, 2013, 8(3): 1349-1376. DOI: 10.1115/1.4023352.
[6] RECUERO A M, ESCALONA J L. Dynamics of the coupled railway vehicle-flexible track system with irregularities using a multibody approach with moving modes [J]. Vehicle System Dynamics, 2014, 52(1): 45-67. DOI: 10.1080/00423114.2013. 857030.
[7] LEI Xiao-yan, WANG Jian. Dynamic analysis of the train and slab track coupling system with finite elements in a moving frame of reference [J]. Journal of Vibration and Control, 2014, 20(9): 1301-1317. DOI: 10.1177/1077546313480540.
[8] YANG Y B, YAU D J, WU S Y. Vehicle-bridge interaction dynamics:with applications to high-speed rail [M]. Singapore: World Scientific Pub Co Inc, 2004.
[9] ZHAI Wan-ming, WANG Kai-yun, CAI Cheng-biao. Fundamentals of vehicle-track coupled dynamics [J]. Vehicle System Dynamics, 2009, 47(11): 1349-1376. DOI: 10.1080/ 00423110802621561.
[10] XIA H, ZHANG N. Dynamic analysis of railway bridge under high-speed trains [J]. Computers & Structures, 2005, 83(23, 24): 1891-1901. DOI: 10.1016/j.compstruc.2005.02.014.
[11] IYENGAR R N, JAISWAL O R. A new model for non-gaussian random excitations [J]. Probabilistic Engineering Mechanics, 1993, 8(3, 4): 281-287. DOI: 10.1016/0266-8920(93)90022-N.
[12] IYENGAR R N, JAISWAL O R. Random field modeling of railway track irregularities [J]. Journal of Transportation Engineering, 1997, 121(4): 303-308. DOI: 10.1061/(ASCE) 0733-947X(1995)121:4(303).
[13] YU Zhi-wu, MAO Jian-feng, GUO Feng-qi, GUO Wei. Non-stationary random vibration analysis of a 3d train–bridge system using the probability density evolution method [J]. Journal of Sound and Vibration, 2016, 366(Supplement C): 173-189. DOI: https://doi.org/10.1016/j.jsv.2015.12.002.
[14] CHEN Jian-bing, SUN Wei-ling, LI Jie, XU Jun. Stochastic harmonic function representation of stochastic processes [J]. Journal of Applied Mechanics, 2013, 80: 1-11. DOI: 10.1115/1.4006936.
[15] XU Lei, ZHAI Wan-ming. Probabilistic assessment of railway vehicle-curved track systems considering track random irregularities [J]. Vehicle System Dynamics, 2018, 56(10): 1552-1576. DOI: 10.1080/00423114.2018.1424916.
[16] XU Lei, ZHANG Qiang, YU Zhi-wu, ZHU Zhi-hui. Vehicle–track interaction with consideration of rail irregularities at three-dimensional space [J]. Journal of Vibration and Control, 2020: 1802499863. DOI: 10.1177/1077546319894816.
[17] MOHAMMADZADEH S, SANGTARASHHA M, MOLATEFI H. A novel method to estimate derailment probability due to track geometric irregularities using reliability techniques and advanced simulation methods [J]. Archive of Applied Mechanics, 2011, 81(11): 1621-1637. DOI: 10.1007/s00419-011-0506-3.
[18] PERRIN G, SOIZE C, DUHAMEL D, FUNFSCHILLING C. Track irregularities stochastic modeling [J]. Probabilistic Engineering Mechanics, 2013, 34: 123-130. DOI: 10.1016/j.probengmech.2013.08.006.
[19] ZHU Meng-yi, CHENG Xiao-hui, MIAO Li-xin, SUN Xin-ya, WANG Shuai. Advanced stochastic modeling of railway track irregularities [J]. Advances in Mechanical Engineering, 2013, 5(6): 401637. DOI: 10.1155/2013/401637.
[20] JIN Z B, QIANG S Z, LI X Z. Perturbation method for train-bridge stochastic structure dynamic analysis [C]// Proceedings of the 3rd International Symposium on Environment Vibrations: Prediction, Monitoring, Mitigation and Evaluation. 2007: 400-405.
[21] MUSCOLINO G, RICCIARDI G, IMPOLLONIA N. Improved dynamic analysis of structures with mechanical uncertainties under deterministic input [J]. Probabilistic Engineering Mechanics, 2000, 15(2): 199-212. DOI: 10.1016/S0266-8920(99)00021-1.
[22] HUANG B, SERESH R F, ZHU L P. Statistical analysis of basic dynamic characteristics of large span cable-stayed bridge based on high order perturbation stochastic FEM [J]. Advances in Structural Engineering, 2013, 16(9): 1499-1512. DOI: 10.1260/1369-4332.16.9.1499.
[23] CAVDAR O, BAYRAKTAR A, ALTUNISIK A. Stochastic seismic analysis of komurhan highway bridge with varying material properties [J]. Civil Engineering and Environmental Systems, 2015, 32(3): 193-205. DOI: 10.1080/10286608. 2015.1013796.
[24] XIN Li-feng, LI Xiao-zhen, ZHU Yan, LIU Ming. Uncertainty and sensitivity analysis for train-ballasted track–bridge system [J]. Vehicle System Dynamics, 2020, 58(3): 1-19. DOI: 10.1080/00423114.2019.1584678.
[25] WAN Hua-ping, NI Yi-qing. An efficient approach for dynamic global sensitivity analysis of stochastic train-track-bridge system [J]. Mechanical Systems and Signal Processing, 2019, 117: 843-861. DOI: 10.1016/j.ymssp.2018.08.018.
[26] HUA L K, WANG Y. Applications of number theory to numerical analysis [M]. Berlin, Heridelberg: Springer, 1981.
[27] LI Jie, CHEN Jian-bing. Probability density evolution method for dynamic response analysis of structures with uncertain parameters [J]. Computational Mechanics, 2004, 34(5): 400-409. DOI: 10.1007/s00466-004-0583-8.
[28] LI Jie, CHEN Jian-bing. Stochastic dynamic of structures [M]. Singapore: John Wiley & Sons(Asia) Pte Ltd, 2009.
[29] LEI Xiao-yan. High speed railway track dynamics: Models, algorithms and applications [M]. Singapore: Springer, 2016.
[30] CHEN Jian-bing, LI Jie. Dynamic response and reliability analysis of non-linear stochastic structures [J]. Probabilistic Engineering Mechanics, 2005, 20(1): 33-44. DOI: 10.1016/j.probengmech. 2004.05.006.
[31] ZENG Qing-yuan, GUO Xiang-rong. Train-bridge time-variant system analysis theory and application [M]. Beijing, China: China Railway Press, 1999. (in Chinese)
[32] YU Zhi-wu, MAO Jian-feng. A stochastic dynamic model of train-track-bridge coupled system based on probability density evolution method [J]. Applied Mathematical Modelling, 2018, 59: 205-232. DOI: 10.1016/j.apm. 2018.01.038.
[33] YU Zhi-wu, MAO Jian-feng. Probability analysis of train-track-bridge interactions using a random wheel/rail contact model [J]. Engineering Structures, 2017, 144: 120-138. DOI: 10.1016/ j.engstruct.2017.04.038.
[34] JOHNSON K L. Contact mechanics [M]. UK: Cambridge University Press, 1985.
[35] KALKER J J. Three-dmensional elastic bodies in rolling contact [M]. The Netherlands: Kluwer Academic Publishers, 1990.
[36] CHEN Guo, ZHAI Wan-ming. A new wheel/rail spatially dynamic coupling model and its verification [J]. Vehicle System Dynamics, 2004, 41(4): 301-322. DOI: 10.1080/ 00423110412331315178.
[37] KALKER J J. On the rolling contact of two elastic bodies in the presence of dry friction [D]. The Netherlands: Delft University, 1967.
[38] FANG Kai-tai. Uniform design: Application of number-theoretic methods in experimental design [J]. Acta Math Appl Sin, 1980, 3(4): 363-372.
[39] FANG Kai-tai, LIN D K. Uniform design in computer and physical experiments [C]// International Workshop on the Grammar of Technology Eevelopment. New York, 2008: 105-125.
[40] ZHOU Yong-dao, FANG Kai-tai. An efficient method for constructing uniform designs with large size [J]. Computational Statistics, 2013, 28(3): 1319-1331. DOI: 10.1007/s00180-012-0359-4.
[41] XU Lei, ZHAI Wan-ming. A new model for temporal-spatial stochastic analysis of vehicle-track coupled systems [J]. Vehicle System Dynamics, 2017, 55(3): 427-448. DOI: 10.1080/00423114.2016.1270456.
[42] WEN De-zhi, ZHUO Ren-hong, DING Da-jie, ZHENG Hui, CHENG Jing, LI Zheng-hong. Generation of correlated pseudorandom variables in monte carlo simulation [J]. Acta Physica Sinica, 2012, 61(22): 514-518. DOI: 10.7498/ aps.61.220204.
[43] ROSENBLATT M. Remarks on a multivariate transformation [J]. Annals of Mathematical Statistics, 1952, 23(3): 470-472. DOI: 10.1007/978-l-4419-8339-8_8.
[44] LI Jie, CHEN Jian-bing. Probability density evolution equations-A historical investigation [J]. Journal of Earthquake and Tsunami, 2009, 3(3): 209-226. DOI: 10.1142/ S1793431109000536.
[45] LI Jie, CHEN Jian-bing. The principle of preservation of probability and the generalized density evolution equation [J]. Structural Safety, 2008, 30(1): 65-77. DOI:10.1016/ j.strusafe.2006.08.001.
(Edited by FANG Jing-hua)
中文导读
基于结构参数不确定的列车-轨道-路基系统耦合振动概率分析
摘要：列车荷载作用下有砟轨道-路基耦合系统结构参数的不确定性引起的随机振动对行车安全的影响不可忽略。本文提出了一种基于概率密度演化理论的三维列车-有砟轨道-路基耦合系统随机振动概率仿真分析模型，该模型可同时考虑轨道随机不平顺、道砟层和路基层随机刚度、随机阻尼等耦合效应，为列车-轨道-路基系统随机振动分析提供了一种全新的计算分析方法。采用数论方法对多维随机参数进行代表性离散数组点设计。结果表明，与蒙特卡罗模拟方法相比，概率密度演化模型开展随机振动分析更为准确、高效。基于算例开展了多维随机参数的敏感性分析，系统地评估了不确定结构随机参数的相对重要性，并在此基础上探讨了列车-轨道-路基系统的随机概率演化机制。
关键词：列车-轨道-路基耦合系统；结构参数不确定性；随机振动；概率密度演化方法；轮轨关系
Foundation item: Projects(51708558, 51878673, U1734208, 52078485, U1934217, U1934209) supported by the National Natural Science Foundation of China; Project(2020JJ5740) supported by the Natural Science Foundation of Hunan Province, China; Project(KF2020-03) supported by the Key Open Fund of State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures, China; Project (2020-Special-02) supported by the Science and Technology Research and Development Program of China Railway Group Limited
Received date: 2020-04-29; Accepted date: 2020-11-26
Corresponding author: XIAO Yuan-jie, PhD, Associate Professor; Tel: +86-731-82656611; E-mail: yjxiao@csu.edu.cn; ORCID: https://orcid.org/0000-0003-4450-9012
Abstract: Random dynamic responses caused by the uncertainty of structural parameters of the coupled train-ballasted track-subgrade system under train loading can pose safety concerns to the train operation. This paper introduced a computational model for analyzing probabilistic dynamic responses of three-dimensional (3D) coupled train-ballasted track-subgrade system (TBTSS), where the coupling effects of uncertain rail irregularities, stiffness and damping properties of ballast and subgrade layers were simultaneously considered. The number theoretical method (NTM) was employed to design discrete points for the multi-dimensional stochastic parameters. The time-histories of stochastic dynamic vibrations of the TBSS with systematically uncertain structural parameters were calculated accurately and efficiently by employing the probability density evolution method (PDEM). The model-predicted results were consistent with those by the Monte Carlo simulation method. A sensitivity study was performed to assess the relative importance of those uncertain structural parameters, based on which a case study was presented to explore the stochastic probability evolution mechanism of such train-ballasted track-subgrade system.
