Article ID: 1003-6326(2005)02-0473-05
Higher order asymptotic fields for mode Ⅰ crack in functionally gradient material
DAI Yao(戴 耀)1, YAN Xiu-fa(燕秀发)1
(Department of Engineering Mechanics, Academy of Armored Force Engineering, Beijing 100072, China)
Abstract:
Higher order stress fields for a mode Ⅰ crack perpendicular to the direction of property variation in a functionally gradient material(FGM), which has an exponential variation of elastic modulus along the gradient direction, were obtained through an asymptotic analysis. The Poissons ratio of the FGMs was assumed to be constant throughout the analysis. The first five terms in the asymptotic expansions of crack tip stress fields were derived to bring out the influence of nonhomogeneity on the structure of the stress field explicitly. The analysis reveals that only the higher order terms in the expansion are influenced by the material nonhomogeneity. Moreover, it can be seen from expressions of higher order stress fields that at least three terms must be considered in the case of FGMs in order to explicitly account for the nonhomogeneity effects on the structure of crack tip stress fields.
Key words:
functionall gradient material; nonhomogeneity; asymptotic expansion; higher order stress fields CLC number: O343.2;
Document code: A
1 INTRODUCTION
More and more attention has been paid to the investigation of so called functionally gradient materials (FGMs) in recent years as their advantages are realized[1]. FGMs consist of two distinct material phases, such as ceramic and metal alloy phases, and are the mixture of them such that the composition of each changes continuously along one direction. FGMs used in high temperature applications have metal and ceramic as their constituents and offer good balance between strength and high temperature resistance. FGMs are unique in that they offer the possibility of tailoring their constituents and gradation to match the end use. Even though the initial research on FGMs is largely motivated by the practical applications of the concept in a wide variety of thermal shielding problems, materials with graded physical properties have almost unlimited potential in many other technological applications.
Experiments have shown that cracks occur in FGMs although the absence of sharp interfaces does alleviate problems with interface fracture and fracture remains a key failure mode of these materials. Obviously, successful application of FGMs depends on an understanding of their fracture behavior. A large body of work has been reported on fracture mechanics of FGMs. Erdogan[2] reviewed the elementary concepts of fracture mechanics of FGMs and identified a number of typical problems relating to fracture of FGM. Gu and Asaro[3] considered a semi-infinite crack in a strip of FGM under edge loading and obtained stress intensity factor(SIF) relations for many commonly used fracture specimen configurations. Santare and Lambros[4] and Marur and Tippur[5] carried out numerical analysis of particulate FGM, and studied the influence of material gradient and crack location on the size of singular fields and the singular behavior of the stress and displacement fields by comparing the FGMs results with that obtained for homogeneous medium. Li and Wang[6] obtained near-tip stress fields for antiplane crack in functionally gradient piezoelectric materials. Crack deflection in FGM was considered by Gu and Asaro[7]who reported the strong influence of material gradient on the crack kink angle when the crack was in the middle of the gradient zone. Shbeeb et al[8, 9] studied interactive multiple crack problems in FGMs and revealed the effects of nonhomogeneity constant, crack orientation, and crack-tip distance on stress intensity factors (SIFs). Surface cracks in FGMs under mode Ⅰ thermomechanical loading were considered by Matthew et al[10] using the domain integral method. Delamination and cracking of FGMs at coating/substrate interfaces due to thermal loads were the focus of investigations by Lee and Erdogan[11] and Gaudette et al[12]. Fujimoto and Noda[13] examined the influence of material gradient and thermal shock on crack propagation. Mentioned above all, the classical inverse square root singular nature of the crack-tip stress field is preserved in FGMs, however, the SIF is influenced by the nonhomogeneity of the material. In addition, the SIFs for cracks in FGMs for different geometry and loading conditions are provided.
The asymptotic behavior of the stress field structure near a crack tip has received very little attention. Most of stress fields currently available are obtained through integral transform method. However, the inversion has to be carried out numerically making these stress field expressions not feasible for extraction of fracture parameters from experimental data. The structure of the stress fields away from crack tip is significantly altered by nonhomogeneity, as demonstrated by Eischen[14]. Parameswaran and Shukla[15, 16] developed the structure of the first stress invariant and the out of plane displacement to bring out the effects of nonhomogeneity. However, nonhomogeneity specific terms for individual stress components have not been developed. Such stress fields are necessary in the analysis of full fields experimental data obtained through techniques such as photoelasticity, coherent gradient and sensing(CGS). In this paper, the asymptotic expansions of stress fields for a mode Ⅰ crack perpendicular to the direction of property variation in a FGM are provided and nonhomogeneity specific terms for individual stress components are developed. The solutions are obtained through an asymptotic analysis assuming an exponential variation of elastic modulus along the gradient direction.
2 THEORETICAL CONSIDERATIONS
The stress function approach of solving plane crack problems leads to a bi-harmonic equation for homogeneous materials. However, in the case of FGMs, due to spatial variation of elastic properties, the governing differential equation contains many lower order differential terms as discussed below in this section, making the solution procedure more involved. Hence, an asymptotic analysis is performed to obtain explicit expressions for the stress field in a series form. The elastic and physical properties of FGMs vary from point to point in the material and the variation is in general limited to a single direction. At a given point in the material, the properties can be assumed to be isotropic, and at a continuum level FGMs are isotropic nonhomogeneous solids.
Consider the plane elastic problem shown in Fig.1 where the medium contains a finite crack on the y=0 plane. 2L is the length of the crack. In previous studies[17], it is shown that the effect of the Possions ratio ν on the crack tip stress field is rather negligible. Thus, it is assumed to be con stant too. The elastic modulus is assumed to vary exponentially in the y direction as given in Eqn.(1):
E=E0eβ y(1)
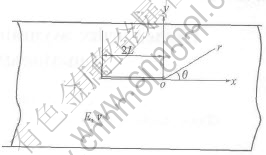
Fig.1 Crack geometry in FGM medium
where E0 is the elastic modulus at the crack tip and β is the nonhomogeneity parameter having dimension [Length]-1 . The in-plane stress components (σij, i, j∈{x, y}) can be defined in terms of the Ariys stress function F=F(x, y), as given by Eqn.(2):
![]()
Substituting Eqn.(2) into the compatibility equation through the HooKes law, for the plane problem, the compatibility equation may be written in rectangular Cartesian coordinates as below:
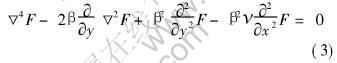
Expressing F(x, y) in terms of polar coordinates as (r, θ), Eqn.(3) can be written in terms of polar coordinates (r, θ) as
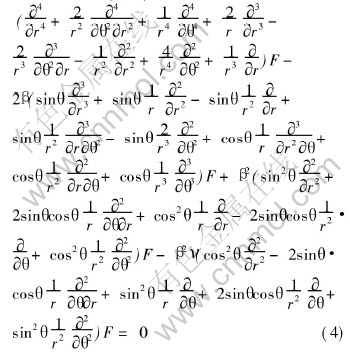
Eqn.(3) or (4) is for the generalized plane stress. The differential equation for plane strain is obtained by replacing ν by ν(1-ν). It may be observed from Eqn.(3) that the first term is the bi-harmonic term and the additional lower differential terms occur due to the nonhomogeneity parameter. The solution for Eqn.(3) or (4) is obtained through an asymptotic analysis approach as explained in the follow section.
3 STRESS FUNCTIONA
For FGMs, the stresses near the crack tip have the conventional inverse square-root singularity[18]. Therefore, it is assumed at this stage F(r, θ) that the stress function can be expanded as follows:
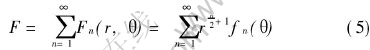
where Fn(r, θ)=r[SX(]n[]2[SX)]+1fn(r, θ).
The above series on substitution into Eqn.(4) leads to an infinite series involving differential equations associated with each power of r as written below:
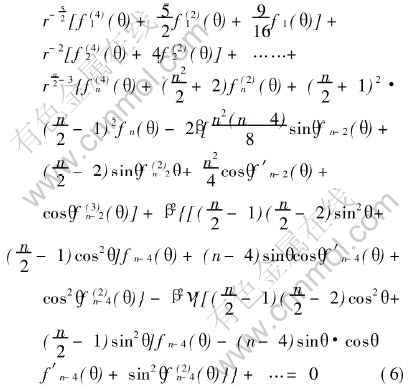
For Eqn.(6) to be valid for any arbitrary r, the differential equations corresponding to each power of r (r-1/2, r0, r1/2, r1, r3/2) should be identically zero. This leads to the following set of differential Eqns.
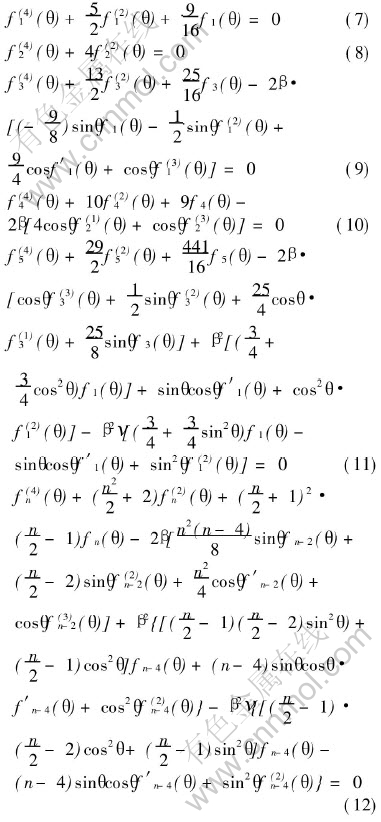
In general, crack faces are supposed to be traction free, which corresponds to the following boundary conditions:
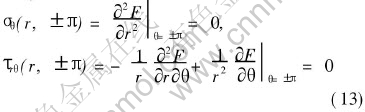
Substituting Eqn.(5) into Eqn.(13), Eqn.(13) reduces to
fn(±π)=0, f′n(±π)=0(14)
From Eqns.(7)-(11) and (14), the functions Fn for n=1, 2, 3, 4, 5 are obtained as

where A13=A11/3, A14=A12, A23=-A21, A33=(-A31+3C31)/5, A34=-A32+C32, C31=-βA12/4, C32=βA11/4, A43=-A41, A44=-A42/3, A53=(-3A51+C51+5C53)/7, A54=-A52+C52+C54,![]() ,
, ![]() ,
, ![]() ,
, ![]() , and A11, A12, A21, A31, A32, A41, A42, A51 and A52 are undetermined coefficients. From Eqn.(12), Fn can be obtained recursively.
, and A11, A12, A21, A31, A32, A41, A42, A51 and A52 are undetermined coefficients. From Eqn.(12), Fn can be obtained recursively.
4 HIGHER ORDER STRESS FIEDS
By substituting Eqns.(15)-(19) into Eqn.(20),

A five-term expansion for crack-tip stresses is obtained as follows:

5 SUMMARY
Higher order stress fields for a mode Ⅰ crack perpendicular to the direction of property variation in a FGM which has an exponential variation of elastic modulus under constant Poissons radio are derived through an asymptotic analysis. The accurate solutions of the problem are presented in the series form. Obviously, the solutions are of important or universal value because they have nothing to do with the specimen geometry and loading conditions. They can be the base of other numeric methods for fracture analysis for FGMs such as the boundary collocation method and the higher order approximate method. At the same time, the explicit form of nonhomogeneity specific higher order terms is developed for FGMs based on which the characteristics of the stress fields and the effect of nonhomogeneity on their structure are brought out. These stress fields are useful in extracting fracture parameters by analyzing full fields around the crack tip obtained through experimental techniques such as photoelasticity and CGS. Through investigating the coefficients, it is shown that the coefficients of r-1/2, r0 in the asymptotic expansion of crack tip stress fields in FGMs are the same as those in homogeneous materials. The result is consistent with those available[14, 17]. Furthermore, it can be seen from that only the terms beyond the order r0 and the order r1 are influenced by the material nonhomogeneity. Therefore, the higher order terms differ considerably from their counterparts for homogeneous materials and alter the nature of stress fields near the crack tip. The analysis presented indicates that at least three terms must be considered in the case of FGMs in order to explicitly account for nonhomogeneity effect on the structure of crack tip stress fields. The effects are dominant in the region around the crack tip from where experimental data is usually sampled, and hence, nonhomogeneity specific higher order terms presented here must be included to obtain meaningful estimate of fracture parameters from experimental data.
REFERENCES
[1]Jedamik R, Neubrand A, Robel J. Production of functionally graded materials from electrochemically modified carbon performs [J]. Journal of American Ceramic Society, 2000, 83(4): 983-985.
[2]Erdogan F. Fracture mechanic of functionally graded materials [J]. Composites Engineering, 1995, 5(7): 753-770.
[3]Gu P, Asaro R J. Cracks in functionally graded material [J]. International Journal of Solids Structures, 1997, 34(1): 1-17.
[4]Santare M H, Lambros J. Use of graded finite elements to model the behavior for nonhomogeneous materials [J]. Journal of Applied Mechanics, 2000, 67(4): 819-822.
[5]Marur P R, Tippur H V. Numerical analysis of crack-tip fields in functionally graded materials with a crack normal to the elastic gradient [J]. International Journal of Solids and Structures, 2000, 37(36): 5353-5370.
[6]Li C Y, Wang G J. Antiplane crack problem in a nonhomogeneous elastic plane [J]. Journal of Applied Mechanics 2002, 69(2): 481-488.
[7]Gu P, Asaro R J. Crack deflection in functionally graded materials [J]. International Journal of Solids and Structures, 1997, 34(21): 3085-3098.
[8]Shbeeb N J, Binienda W K, Kreider K L. Analysis of driving forces for multiple cracks in an infinite nonhomogeneous plate(part Ⅰ)—theoretical analysis [J]. Journal of Applied Mechanics, 1999, 66(2): 492-500.
[9]Shbeeb N J, Binienda W K, Kreider K L. Analysis of driving forces for multiple cracks in an infinite nonhomogeneous plate(part Ⅱ): Numerical Solutions [J]. Journal of Applied Mechanics, 1999, 66(2): 501-506.
[10]Matthew C W, Glaucio H P, Robert H, et al. Stress-intensity factors for surface cracks in functionally graded materials under mode(Ⅰ): thermomechanical loading [J]. International Journal of Solids and Structures, 2003, 41(8): 1081-1118.
[11]Lee Y D, Erdogan F. Interface cracking coating under stead-state heat flow [J]. Engineer Fracture Mechanics, 1998, 59(3): 361-380.
[12]Gaudette F G, Giannakopoulos A F, Suresh S. Interface cracks in layered materials subjected to a uniform temperature change [J]. International Journal of Fracture, 2001, 110(4): 325-329.
[13]Fujimoto T, Noda N. Influence of the compositional profile of functionally graded material on the crack path under thermal shock [J]. Journal of American Ceramic Society, 2001, 84(7): 1480-1486.
[14]Eischen J W. Fracture of nonhomogeneous materials [J]. Journal of Fracture, 1987, 34(1): 3-22.
[15]Parameswaran A, Shukla V. Crack-tip stress fields for dynamic fracture in functionally graded materials [J]. Mechanics of Material, 1999, 31(9): 579-596.
[16]Parameswaran A, Shukla V. Asymptotic stress fields for stationary cracks along the elastic gradient in functionally graded materials [J]. Journal of Applied Mechanics, 2002, 69(1): 240-243.
[17]Delale F, Erdogan F. The crack problem for a nonhomogeneous plane [J]. Journal of Applied Mechanics, 1983, 50(3): 609-614.
[18]Jin Z H, Noda N. Crack-tip singular fields in nonhomogeneous materials [J]. Journal of Applied Mechanics, 1994, 61(3): 738-740.
Foundation item: Projects(90305023; 59731020) supported by the National Natural Science Foundation of China
Received date: 2004-12-14; Accepted date: 2005-01-18
Correspondence: DAI Yao, Professor, PhD; Tel: +86-10-66719427; E-mail: yao_dai@yahoo.com.cn


