Solidification and remelting of Al through Al2O3 fibrous preform under centrifugal force
HU Guo-xin(胡国新), LIU Jian-ju(刘建局), ZHANG Li-xiang(张利祥), TIAN Qin-wei(田芩蔚)
School of Mechanical and Power Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
Received 28 July 2006; accepted 15 September 2006
Abstract:
The solidification and remelting of molten aluminum through a porous preform under centrifugal force field were modeled numerically. The results show that the transient solidification and remelting phenomena appear on the infiltration front and can be divided into two distinct regions: the remelting region and solid-liquid congruent melting region. The decrease of porosity always results in the increase of moving velocity difference between the infiltration front and the remelting front, which leads to the increase of the solid-liquid congruent region extent. But for the decrease of the rotational frequency, the difference of moving velocity between infiltration front and remelting front decreases, which leads to the decrease of regional extent. The infiltration front moving velocity is mainly influenced by the centrifugal infiltration pressure, whereas the remelting front moving velocity is mainly influenced by the material thermodynamics. The transient solidification and remelting phenomena are the intercoupling results between the centrifugal infiltration dynamics and the material thermodynamics.
Key words:
fibrous preform; centrifugal infiltration casting; solidification; remelting; heat transfer;
1 Introduction
Due to the increasing use and importance of the metal-matrix composites (MMCs), their fabrication techniques have been subjected to continuous development during the last few years. The centrifugal infiltration casting has been testified to be an effective method to manufacture high quality metal-matrix composites. In the recent years many researches have been carried out for investigating the heat transfer between the molten metal and the porous media in the centrifugal infiltration and squeeze casting process [1]. MORTENSEN et al [2-3] and HU et al [4] investigated the unidirectional infiltration and heat transfer of the fibrous preform by a pure metal or a binary alloy in the squeeze casting by the assumption of the thermal equilibrium between the preheated fibrous preform or particulate and the high temperature molten metal. They found if the fibrous preform or particulate was preheated at a relative low temperature, the solid-liquid congruent melting region would come into being at the beginning of the infiltration casting process, with the infiltration advance, the remelting phenomenon would occur in the partial solidification region for the continuous heat transfer from the inlet region to the infiltration front. TONG et al [5-6] established an infiltration and heat transfer model in the squeeze casting accompanied with solidification and remelting. LEE et al [7] fabricated the metallic amorphous phase reinforced metal matrix composites by using the infiltration casting process.
However, only a few papers have been published on the centrifugal infiltration of the molten metal in the last few years. LU et al [8] and OGURTSOV et al [9] investigated the influence of the centrifugal force on solidifying process in big space. WANG et al [10] discussed the relationship among the pouring temperature of liquid metal, centrifugal force, ceramic particles pre-heat treatment temperature, ceramic particle sizes and composite layer depth in the filling process of the centrifugal infiltration casting systematically. HU et al [11-12] investigated the infiltration and heat transfer model of the molten metal. WANNASIN and FLEMINGS [13] investigated the fabrication of metal matrix composites by a high-pressure centrifugal infiltration process. Infiltration phenomena of molten metal through porous preform in a centrifugal force field were analyzed by NISHIDA et al [14-15], but in NISHIDA’s paper, no transient solidification and remelting phenomena occurred in the theory models for filling process of centrifugal infiltration casting. It was difficult to obtain the appropriate infiltration conditions by experimental work, and so a theoretical analysis would be helpful to understand the transient solidification and remelting in a porous preform.
So in this paper NISHIDA model mainly concerns with the infiltration and heat transfer with the transient solidification and remelting phenomena in the centrifugal infiltration process. The objective of the paper is to investigate the transient temperature distribution, the length of the remelting region and the solid-liquid congruent melting region and the transient solidification volume fraction at different operating conditions aiming at understanding the transient solidification and remelting phenomena in the centrifugal infiltration casting process deeply.
2 Mathematical and physical model
A schematic drawing of the centrifugal infiltration casting is shown in Fig.1. Different from the pressure infiltration processing, the molten pure aluminum with an initial temperature, Tm,in, cast into the graphite container begins to infiltrate into the porous preform by the generated centrifugal force. In the simulation, the preform is assumed to be made of fibrous Al2O3. Three different regions are formed in the process of the centrifugal infiltration: the remelting region, the solid-liquid congruent melting region and the uninfiltrated region of the preform. The terms r0, r1 and r2 denote the initial location of the inner surface of molten aluminum, the locations of the inner and outer surface of the preform, respectively and rf is the location of the infiltration front in the preform, rs is the location of the inner surface of the molten metal.
In detail, at the beginning of the infiltration when the preheated temperature of the fibrous preform is below the melting point of the metal, the partial solidification occurs as the molten metal infiltrates through the preform, which is called as the solid-liquid congruent melting region. With the advance of infiltration, heat transfer is conducted from the inlet region to the infiltration front continuously and one part of the solid-liquid congruent melting region Ⅱwould remelt, which forms the remelting region Ⅰ in the former part of the preform, where only the molten metal exists. As the temperature decreases along r direction, the other part of solid-liquid congruent melting region Ⅱ remains and locates between the remelting front rL and the infiltration front rf.
The molten metal flow with heat transfer through Al2O3 porous preform is a complex process, the hypotheses and simplifications can refer to Ref.[11]. The molten metal flow through Al2O3 fibrous preform is described by the equation of momentum conservation based on the Darcy theory.
(1)
(2)
where u is the radial superficial velocity, and μ is the viscosity of the molten metal, p is the average pressure, ω(w=2πN, N is the number of revolution per second) is the rotational frequency in the centrifugal force field, κ is the permeability of the porous media.
Combining Eqn.(1) with Eqn.(2), the pressure distribution in the infiltrated region is given by
(3)
where pc denotes the threshold pressure which can be calculated by MORTENSEN’s formula as[16]
(4)
The surface energy of molten aluminum γ and the contact angle θ are given in Ref.[17].
=0.893 Pa·m, θ=160?
After the infiltration starts, the location of the inner surface of molten aluminum, rs, moves along the radial direction. It follows the law of conservation of mass and is given by: rs = r0+ε(rf-r1). The pressure pin(t) on the inner surface of the preform is given by
(5)
On the infiltration front, the superficial velocity:
(6)
where ε2 represents the porosity of the liquid-solid congruent melting region. When r=rf, p=pc, the infiltration front rf(t) can be described as the following equations:
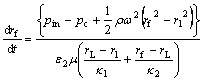(7)
where κ1 and κ2 are the Darcy permeability of the remelting region and the liquid-solid congruent melting region, respectively.
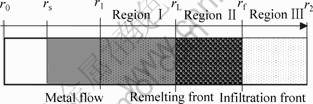
Fig.1 Schematic diagram of centrifugal infiltration casting
The formulation between the permeability κ and the porosity ε for Al2O3 preform is given as
(8)
where C =150 is an empirical constant given by Ergun.
For pure metal matrix composites, the solid-liquid congruent melting phenomena only take place at the melting point temperature TE. T2 is equal to TE in the solid-liquid congruent melting region Ⅱ, so no heat transfer occurs in this region. Based on the assumption that the molten metal and solid phase are local thermal equilibrium, the energy equation for the remelting region Ⅰ is given by
(9)
The energy equation for the uninfiltrated region Ⅲ takes the following form:
(10)
where ρ, C and λ denote the density, the specific heat and the thermal conductivity, respectively, the subscripts c, s and m denote the infiltration composite layer, the Al2O3 fibre and the molten aluminum.
(11)
(12)
In region Ⅱ, due to the partial molten metal solidified on the surface of Al2O3 fibrous preform, the solid volume fraction Vs increases. The increased volume fraction 
and increased fibrous radius R′ are
(13)
(14)
where Ro is the fibrous radius without solidification, gs is the solid volume fraction.
The boundary conditions are given as
The beginning of infiltration, r = r1:
p=pin, T=Tm,in (15)
The interface of region Ⅰ and Ⅱ, r = rL:
p1=p2, T1=T2=TE, u1=u2,
, 
(16)
The interface of regions Ⅱ and Ⅲ, r=rf:
T2=T3=TE, 
,
, 
(17)
The outer surface of region Ⅲ, r=r2:
(18)
The initial conditions are given as
, 
, 
(t=0) (19)
where uL is the remelting front moving velocity, 
is the latent heat of the liquid-solid phase change, α0 is the heat convective coefficient between the container and the atmosphere, λb is the effective thermal conductivity of the graphite container, L is the container height, Tb is the temperature of the container’s outer surface, T0 is the surrounding temperature.
The above equations were discretized by the implicit TDMA algorithm and the first kind of first-order upwind difference method. A uniform grid of 1 000 was adopted for the computations of this one-dimensional model. In the simulations, the preheated temperature of Al2O3 preform is 703 K, the initial temperature of the pure Al Tm,in is 1 173 K. Other parameters can refer to Ref.[12].
3 Results and discussion
Fig.2 shows the transient temperature distribution in the infiltrated region at n=50 r/s. The infiltration region can be distinctly divided into two different portions based on the melting point temperature of the aluminum. The former portion where the temperature is beyond the melting point temperature is regarded as the remelting region and it is close to the inlet. The latter portion, which shows as the horizontal line, denotes the solid-liquid congruent melting region and it lies between the remelting front and the infiltration front. It can be indicated from Fig.2 that the partial solidification would take place on the fibrous prefrom surface at the infiltration front, when the preheated temperature of the prefrom is lower than the melting point temperature. With the advance of infiltration, the heat is conducted from the inlet region to the infiltration front continuously and the remelting phenomena would appear. It can also be seen from Fig.2 that the length of the horizontal line increases constantly as the infiltration advances. This means that the transient partial solidification region extends continuously as the region moves on. This is because the thermoresistance increases with the composite layer thickness (rf-r1). However, in the uninfiltrated region of fibrous preform, its temperature maintains constant as a result of the occurrence of little heat transfer.
Fig.2 Variation of temperature distribution with time in infiltrated region
The functional curve of the infiltration distance vs time is shown in Fig.3 for n=50 r/s. The preheated temperature of Al2O3 preform is 703 K, so the transient solidification and remelting phenomena should be taken into consideration, which is different from Ref.[15] that the preheated temperature of Al2O3 preform is higher than the melting point temperature of the aluminum, where the transient solidification phenomenon in molding process is neglected. It is obvious that the transient solidification and remelting phenomena have great effects on the infiltration velocity. Under the same infiltration conditions, the infiltration velocity calculated by this model is greater than the numerical value in Ref.[15], because the effective porosity decreases due to the appearance of the transient solidification region on the infiltration front.
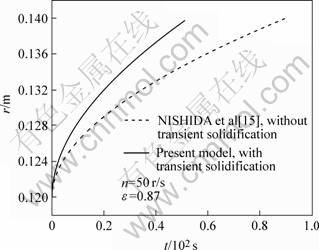
Fig.3 Relationship between infiltrated distance and time
Fig.4 shows the transient distribution of the infiltration front rf, and the remelting front rL. Fig.5 shows the solid volume fraction for solid-liquid congruent melting region gs for the porosity ε in the range of 0.87, 0.91 and 0.94. Several conclusions can be obtained by analyzing Figs.4 and 5 as: 1) The transient partial solidification almost takes place at the beginning of the infiltration where form a solid-liquid congruent melting region, whereafter the remelting front rL and the solid-liquid congruent melting region move on continuously with the infiltration advance. The length (rf-rL) and the solid volume fraction gs of the solid-liquid congruent melting region increase with the infiltration advance. 2) The slope rate of the curves for rf(t) and rL(t) denote the infiltration front moving velocity drf/dt and the remelting front moving velocity drL/dt. As we know that the infiltration front moving velocity drf/dt is mainly influenced by the factors of the infiltration dynamics such as the centrifugal infiltration pressure, etc., whereas the remelting front moving velocity drL/dt is mainly influenced by the factors of the material thermodynamics such as the thermoconductivity and the phase change characters of metal, etc. So when drf/dt=drL/dt, the solid-liquid congruent melting region would not exist in the infiltration process. When drf/dt>drL/dt, the solid-liquid congruent melting region would appear certainly. The regional length of the solid-liquid congruent melting region (rf-rL) indicates the intercoupling results between the centrifugal infiltration dynamics and the composite material thermodynamics in infiltration process. 3) When the porosity of preform decreases, the infiltration front and the remelting front moving velocities decrease and the solid volume fraction gs for the solid-liquid congruent melting region increase.
Figs.6 and 7 show the influence of rotational frequency on the transient solidification and remelting phenomena. With the decrease of rotational frequency, it needs long time to complete the infiltration, the length of the solid-liquid congruent melting region decreases, the solid volume fraction in this region increases, the infiltration front and remelting front moving velocities decrease and their difference also decreases. When n=30 r/s, the moving velocity of the remelting front approaches that of the infiltration front. The metal of partial solidification on the interface remelts quite soon, and no solid-liquid congruent melting region appears in the infiltration process. The infiltration velocity would decrease whether the porosity of preform or the rotational frequency recedes, which would lead to the increase of the solid volume fraction in the solid-liquid congruent melting region. This is because the heat transfer rate by the liquid infiltration has dominant effect on the transient solidification phenomenon in the infiltration process, with the transient volume fraction increase to a certain value, the infiltration process would stop due to the large infiltration resistance which can not be overwhelmed by the force generated by the centrifugal infiltration, particularly for the situation of a relatively low preheated temperature of preform and the superheat temperature of molten metal.
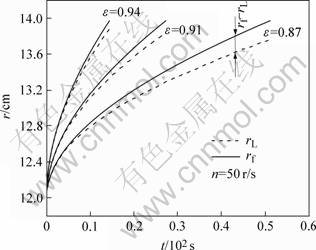
Fig.4 Influence of porosity on regional extent for solid-liquid congruent melting region
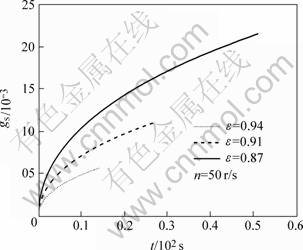
Fig.5 Influence of porosity on solid volume fraction for solid-liquid congruent melting region
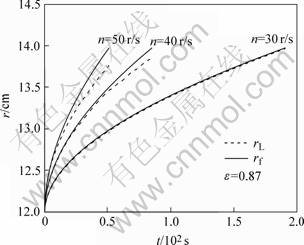
Fig.6 Influence of rotational frequency on regional extent for solid-liquid congruent melting region
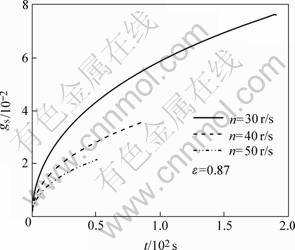
Fig.7 Influence of rotational frequency on solid volume fraction for solid-liquid congruent melting region
4 Conclusions
1) When the preheated temperature of Al2O3 fibrous preform is lower than the melting point temperature, transient solidification and remelting phenomena appear on the infiltration front and it can be divided into two distinct regions: the remelting region and the solid-liquid congruent melting region. The solid-liquid congruent melting region moves on and its regional length and solid volume fraction increase with the infiltration advance.
2) The decrease of the infiltration and remelting front moving velocities and the increase of solid volume fraction of the solid-liquid congruent melting region are induced by either the decrease of porosity or rotational frequency. Nevertheless, the decrease of porosity always results in the increase of moving velocity difference between the infiltration front and the remelting front, which leads to the increase of the solid-liquid congruent region extent. But for the decrease of the rotational frequency, the difference of moving velocity between infiltration front and remelting front decreases, which leads to the regional extent decrease.
3) The infiltration front moving velocity drf/dt is mainly influenced by the factors of the infiltration dynamics such as the centrifugal infiltration pressure, whereas the remelting front moving velocity drL/dt is mainly influenced by the factors of the material thermodynamics such as the thermoconductivity and phase change characters of metal. The transient solidification and remelting phenomena are the intercoupling results between the centrifugal infiltration dynamics and the material thermodynamics.
Nomenclature
gs solid volume fraction, %
Tm,in initial temperature of the pure aluminum, K
r0 initial location of the inner surface of molten aluminum, m
r1 locations of the inner surface of the perform, m
r2 locations of the outer surface of the perform, m
rf location of the infiltration front, m
rl remelting front, m
rs location of the inner surface of molten aluminum, m
TE melting point temperature, K
ε porosity, %
F generating force by centrifugal infiltration, N
S cross section area, m2
ρm density of the molten aluminum, kg/m3
pc critical pressure, Pa
ω rotational frequency, rad/s
γ surface energy of molten aluminum, N·m
θ contact angle, rad
uf superficial velocity, m/s
uL movement velocity of remelting front, m/s
ε2 porosity of solid-liquid congruent melting region, %
Pin pressure at the beginning of the infiltration, Pa
κ1 Darcy permeability of remelting region, m2
κ2 Darcy permeability of transient solidification region, m2
ρc density of composite, kg/m3
ρs density of Al2O3 fibre, kg/m3
T1 temperature in region Ⅰ, K
T2 temperature in region Ⅱ, K
T3 temperature in region Ⅲ, K
λc thermal-conductivity coefficient of composite, W/(m·K)
λs thermal-conductivity coefficient of Al2O3 fibre, W/m·K
Cc specific heat capacity of composite, kJ/(kg·K)
Cs specific heat capacity of Al2O3 fibre, kJ/(kg·K)
Cm specific heat capacity of molten aluminum, kJ/(kg·K)
Vs volume fraction of the Al2O3 fibre, %
Vm volume fraction of the molten aluminum, %
increased volume fraction of the Al2O3 fibre, %
increased particulate radius, m
R0 particulate radius, m
N number of revolutions per second
t time, s
ΔH latent heat of liquid-solid phase change, kJ/kg
Subscript
c composite
s Al2O3 fibre
m molten aluminum
References
[1] EARDLEY E S, FLOWER H M. Infiltration and solidification of commercial purity aluminium matrix composites [J]. Materials and Engineering A, 2003, 359: 303-312.
[2] MORTENSEN A, MASUR L J. Infiltration of fibrous preforms by a pure metal: part I. Theory [J]. Metallurgical Transactions A, 1989, 20: 2535-2547.
[3] MORTENSEN A, MICHAUD V. Infiltration of fiber preforms by a binary alloy: part I. theory [J]. Metallurgical Transactions A, 1990, 21: 2059-2071.
[4] HU R, LI H L, WEI M. Theoretical analysis on squeeze infiltration processing of aluminum borate whisker reinforced Al composite [J]. Acta Materiae Composite Sinica, 2002,19: 62-65.
[5] TONG X, KHAN J A. Infiltration and solidification/remelting of a pure metal in a two-dimensional porous preform [J]. Journal of Heat Transfer, 1996, 118: 173-180.
[6] KHAN J A, TONG X. Unidirectional infiltration and solidification/remelting of Al-Cu alloy [J]. Journal of Thermophysics and Heat Transfer, 1998, 12: 100-106.
[7] LEE M H, KIM J H, PARK J S, KIM J C, KIM W T, KIM D H. Fabrication of Ni-Nb-Ta metallic glass reinforced Al-based alloy matrix composites by infiltration casting process[J]. Scripta Materialia, 2004, 50: 1367-1371.
[8] LU J W, CHEN F. Rotation effect on the convection of binary alloys unidirectionally solidified from below[J]. Int J Heat Transfer, 1997, 40: 237-246.
[9] OGURTSOV A P, MILEN’KIJ I A, SAMOKHVALOV S E. Numerical method for calculating the filling of a mold and heat transfer of a melt under the action of centrifugal forces[J]. Inzhenerno-Fizicheskii Zhurnal, 1995, 68: 678-686.
[10] WANG Y W, LIU J P AND SHI T Z. A development study of surface wear-resistance composites with ferrite-based SiC ceramic particles[J]. Foundry, 1990, 11: 15-20.
[11] HU G X, TIAN Q W, WANG G X. Heat transfer of molten aluminum infiltrate through SiC preform in a centrifugal force field [J]. Journal of Chemical Industry and Engineering, 2002, 53: 708-714. (in Chinese)
[12] HU G X, TIAN Q W, WANG G X. Infiltration of molten aluminum and heat transfer in centrifugal casting processes [J]. Acta Materiae Composite Sinica, 2002, 19: 25-30.
[13] WANNASIN J, FLEMINGS M C. Fabrication of metal matrix composites by a high-pressure centrifugal infiltration process [J]. Journal of Materials Processing Technology, 2005, 169: 143-149.
[14] NISHIDA Y, SHIRAYANAGI I, SAKAI Y. Infiltration of fibrous preforms by molten aluminum in a centrifugal force field[J]. Metallurgical and Materials Transaction A, 1996, 27: 4163-4169.
[15] NISHIDA Y, OHIRA G. Modelling of infiltration of molten metal in fibrous preform by centrifugal force[J]. Acta Mater, 1999, 47: 841-852.
[16] MORTENSEN A, CORNIC J A. On the infiltration of metal matrix composites [J]. Metallurgical Transactions A, 1987, 18: 1160-1163.
[17] BRENNAN J J, PASK J A. Effect of nature of surfaces on wetting of sapphire by liquid aluminum [J]. J Am Ceram Soc, 1968, 51: 569-573.
(Edited by LONG Huai-zhong)
Foundation item: Project(50646024) supported by the National Natural Science Foundation of China; Project(20050248021) supported by the Research Fund for the Doctoral Program of Higher Education of China
Corresponding author: HU Guo-xin; Tel: +86-21-62812034; E-mail: hugx@sjtu.edu.cn
