基于多目标优化算法求解非线性互补问题
雍龙泉
(陕西理工学院 数学系, 陕西 汉中，723001)
摘 要：
题解存在的情况下，给出求解此类问题的一类新的算法。首先将非线性互补问题转化为多目标优化，给出多目标优化问题零有效解的定义；进而得到多目标优化问题的零有效解，即非线性互补问题的最优解，最后采用极大极小方法求解转化后的多目标优化问题。数值模拟结果表明该方法的正确性和有效性.
关键词：
中图分类号：O221 文献标志码：A 文章编号：1672-7207(2011)S1-0596-04
Solving nonlinear complementarity problem based on multiobjective optimization
YONG Long-quan
(Department of Mathematics, Shaanxi University of Technology, Hanzhong 723001, China)
Abstract：A new method was proposed for the nonlinear complementarity problem (NCP) under the condition that the solution exists. The NCP was formulated into a multiobjective optimization problem (MOP), and a zero-efficient solution of the MOP was defined. Then the zero-efficient solution of the MOP was also indicated to be the solution of the NCP. Finally the minimax method was used for the MOP. Numerical results indicate that the proposed method is effective.
Key words：nonlinear complementarity problem; multiobjective optimization problem; minimax method
互补问题是由美国的Cottle在其1964年首先提出的，它由线性规划与非线性规划的推广而形成的, 所以其算法研究与可解性研究一样，受到了研究者的重视。互补问题的研究包括：可解性、解集的拓扑性质、稳定性、误差界以及不同类型的互补问题的算法研究等。互补问题被提出后, 很快在工程技术中得到了广泛应用, 许多研究讨论了它在力学、交通、经济、金融、控制等许多领域中的应用[1-2]。
互补问题可定义为, 求一个向量
满足
。如果互补问题中F(x)是线性函数, 即F(x)=Mx+q, 其中M是一个n×n的矩阵, 则称为线性互补问题(简记为LCP)，q是n维向量；如果F(x)是非线性函数, 则称为非线性互补问题(简记为NCP)。比互补问题更为广泛应用的一类问题叫变分不等式问题(VIP(S, F)), 即求向量
, 使得
, 其中
的一个映射, 
是一个非空闭凸集。当S为Rn的非负卦限时, VIP(S, F)和NCP(F)是完全等价的[3]。
关于非线性互补问题的研究一般分为理论和算法两方面，前者主要研究解的存在性、唯一性、稳定性与灵敏度分析,以及互补问题与其他数学问题的联系等；后者则主要建立有效的求解方法以及相应的算法理论分析。至20世纪80年代中后期，经过20余年的努力，在理论与算法方面已取得了比较丰硕的成果。由于与最优化、变分不等式、平衡问题、对策论、不动点理论等数学分支的紧密联系，以及在科技与经济方面的广泛应用，互补问题越来越显示其重要性，这激励人们对其理论与算法的进一步研究，出现了20世纪90年代以来的研究高潮。在这十余年的时间里，人们不仅改进与丰富了互补问题的理论研究，而且还提出多种有效算法。在国际上近十年期间所研究出来的新理论成果和新数值方法包括例外簇和互补问题的可解性、误差界、投影法、非光滑牛顿法、光滑牛顿法和内点法等[4-6]。光滑牛顿法已成为非线性互补问题研究热点。光滑牛顿法的一个重点问题就是NCP函数的构造, 因为许多算法都是通过构造NCP函数将互补问题转化为方程组或最小化问题来进行求解的。函数
称为是NCP函数, 如果
。常见NCP函数有Fisher- Burmeister函数、CHKS函数，更多的NCP函数可以参考韩继业的专著《非线性互补理论与算法》。因此，如何构造一个好的NCP函数，是求解互补问题的关 键[7-8]。许多学者在这方面做了开创性的工作，他们分别构造了不同的NCP函数，并分别建立了求解互补问题的新的算法[6-8]。近年来，随着各种群体智能优化算法的出现，也开始尝试用智能算法来求解互补问题。具体方法就是把互补问题转化为一个无约束优化问题，然后用智能算法进行求解[9-10]。
在解存在的情况下，本文作者给出求解非线性互补问题的一类新算法。具体做法是把非线性互补问题转化为多目标优化问题，借助于多目标优化有效解的定义，给出了零有效解的定义; 进而得到多目标优化问题的零有效解就是非线性互补问题的最优解，最后采用极大极小方法求解转化后的多目标优化问题。数值实验结果表明了该方法的正确性和有效性。
1 问题的转化
本研究的非线性互补问题(P1)如下：
(1)
其中，，
是连续可微函数。 记(P1)的可行域为
，假设可行域
且(P1)的最优解存在。
记
考虑如下多目标优化问题(P2)
(2)
定义1 设
， 若对任意
， 都有
成立， 则称x*为问题(P2)的最优解。
定义 2 若， 且不存在另一个可行点
， 使得
成立， 且其中至少有一个严格不等式成立， 则称x*是问题(P2)的一个有效解(Efficient solution)。 记问题(P2)的有效解集合为XE。
有效解又称Pareto最优解、非劣解(non-inferior solution)、非支配解(non-dominated solution)等[11]。
类似于文献[12-14]中的研究线性互补问题的方法，给出零有效解的定义。
定义3 若
，且有
成立，则称x为问题(P2)的零有效解(Zero-efficient solution)。
于是可以得到如下结论。
定理1 若是问题(P2)的零有效解当且仅当x是问题(P1)的最优解。
证明 若是问题(P2)的零有效解， 根据可行性则
， 又因为
， 从而
因此，x是问题(P1)的最优解。反之， 若x是问题(P1)的最优解， 则， 
， 且不存在另一个可行点， 使得
。因此，x是问题(P2)的零有效解。
定理1给出了一个求解非线性互补问题的新思路， 通过求出多目标优化问题(P2)的零有效解， 就可以获得非线性互补问题的最优解。
下面采用极大极小方法来求解多目标优化问题(P2)的有效解。
2 极大极小法求解多目标优化问题
问题(P2)的极大极小模型(P3)如下：
(3)
式中：
。根据定理1和多目标优化的相关知识，得到如下推论。
推论1 问题(P3)的最优解是问题(P2)的有效解。
推论2 若问题(P3)的最优解x*是问题(P2)的零有效解，则x*也是问题(P1)的最优解。
为了快速求解问题(P3)，提供下列2种方法[15-16]。
(1) 直接采用Matlab中的极大极小函数fminimax求解问题(P3)，从而也就得到问题(P2)的有效解。
(2) 可以采用Matlab中的约束优化函数fmincon求解， 具体方法如下：
由于函数
是不可微的，因此，问题(P3)是一个不可微优化。引进极大熵函数
，其中p>0为控制参数；
关于熵函数的导出可以参考文献[10，17]，熵函数也称凝聚函数，该函数从数学上是以原来函数fi(x)的指数函数构成向量函数的Lp范数的自然对数。 先头的指数变换使向量的各分量为正，后面的对数变换使函数值复原。当p趋于无穷大时，fp(x)在整个空间上一致逼近f(x)。由此可知，只要参数p充分大时，就可以用极大熵函数fp(x)直接代替极大值函数f(x)。 因此，可以通过求解问题(P4)来近似得到问题(P3)的最优解。
(4)
问题(P4)是一个典型的约束非线性规划，采用约束优化函数fmincon进行求解，就得到问题(P2)的有效解。
为了计算方便， 本文作者直接采用极大极小函数fminimax求解问题(P3)。
3 数值实验
为了测试本方法的求解性能，选取如下6个(解存在的)非线性互补标准测试函数[18-20]进行数值计算，这些算例常用在变分不等式和互补问题的求解中。
算例1 求解如下非线性互补问题， 其中
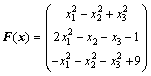(5)
求解此非线性互补问题等价于求解如下多目标优化问题
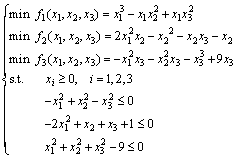(6)
采用函数fminimax求得对应的极大极小问题的最优解为
， 验证可知是问题(P2)的零有效解，从而非线性互补问题的解为。
算例2 求解如下非线性互补问题， 其中
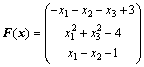(7)
转化为等价的多目标优化问题(P2)， 采用函数fminimax求得相应的极大极小问题的最优解为
， 验证可知是问题(P2)的零有效解， 从而非线性互补问题的解为。
算例3 求解如下非线性互补问题， 其中
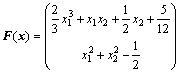(8)
转化为等价的多目标优化问题(P2)， 采用函数fminimax求得极大极小问题的最优解
，验证可知是问题(P2)的零有效解，从而非线性互补问题的解为。
算例4 求解如下非线性互补问题， 其中
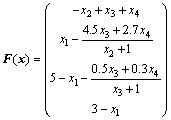(9)
转化为等价的多目标优化问题(P2)， 采用函数fminimax求得其极大极小问题的最优解
，验证可知是问题(P2)的零有效解，从而非线性互补问题的解为。事实上， 该问题的最优解为
。 本方法执行1次只能得到1个零有效解。若要得到多个不同的零有效解，则需要多次执行该算法，且每次需要选取不同的初始点。
算例5 求解Kojima-shindo问题， 其中
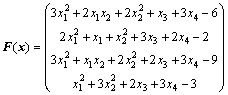(10)
转化为等价的多目标优化问题(P2)， 采用函数fminimax求得其极大极小问题的最优解
，验证可知是问题(P2)的零有效解，从而非线性互补问题的解为。此问题还有一个退化解为
， 本文方法求出了此问题的非退化解。
算例6 求解如下非线性互补问题， 其中
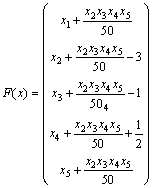(11)
转化为等价的多目标优化问题(P2)， 采用函数fminimax求得极大极小问题的最优解
， 验证可知是问题(P2)的零有效解， 从而非线性互补问题的解为。
4 结束语
给出求解非线性互补问题的一个新的方法: 转化为多目标优化进行求解， 并证明了多目标优化的零有效解就是非线性互补问题的最优解。6个互补问题标准测试函数计算结果表明，该方法是有效的，因此，也是对互补问题算法的一个重要补充和完善。
参考文献：
[1] Billups S C, Murty K G. Complementary problems [J]. Journal of Computational and Applied Mathematics, 2000, 124: 303-318.
[2] Ferris M C, Pang J S. Engineering and economic applications of complementary problems [J]. SIAM Review, 1997, 39: 669-713.
[3] Ferris M C, Pang J S. Complementarity and variational problems: State of the Art[R]. Philadelphia, Pennsylvania, SIAM Publications, 1997.
[4] Harker P T, Pang J S, Harker P T, et al. Finite-dimensional variational inequality and nonlinear complementary problems, a survey review of theory, algorithms and applications [J]. Math Prog, 1990, 48: 161-220.
[5] Pardalos P M, Resende M G C. Handbook of applied optimization [M]. New York: Oxford University Press, 2002: 514-530.
[6] 韩继业, 修乃华, 戚厚铎. 非线性互补理论与算法[M]. 上海: 上海科学技术出版社, 2006.
HAN Ji-ye, XIU Nai-hua, QI Hou-dou. Nonlinear complementary theory and algorithms[M]. Shanghai: Shanghai Science and Technology Press, 2006.
[7] Sun D, Qi L Q. On NCP-functions [J]. Comput Optim Appl, 1999, 13: 201-220.
[8] Chen J S, Pan S. A family of NCP-functions and a descent method for the nonlinear complementary problem [J]. Computational Optimization and Applications, 2008, 40: 389-404.
[9] 张建科. 非线性互补问题的粒子群算法[J]. 计算机工程与应用, 2009, 45 (27): 43-45.
ZHANG Jian-ke. Particle swarm optimization for nonlinear complementary problems[J]. Computer Engineering and Applications, 2009, 45(27): 43-45.
[10] 雍龙泉, 陈涛, 张建科. 求解互补问题的极大熵差分进化算法[J]. 计算机应用研究, 2010, 27(4): 1308-1310.
YONG Long-quan, CHEN Tao, ZHANG Jian-ke. Solving complementary problem based on maximum-entropy differential evolution algorithm[J]. Application Research of Computers, 2010, 27(4): 1308-1310.
[11] Chinchuluun A, Pardalos P M. A survey of recent developments in multiobjective optimization [J]. Annals of Operations Research, 2007, 154(1): 29-50.
[12] Kostreva M M, Wiecek M M. Linear complementary problems and multiple objective programming [J]. Mathematical Programming, 1993, 60: 349-359.
[13] Isac G, Kostreva M M, Wiecek M M. Multiple objective approximation of feasible but unsolvable linear complementary problems [J]. Journal of Optimization Theory and Applications, 1995, 86: 389-405.
[14] Kostreva M M, Yang X Q. Unified approaches for solvable and unsolvable linear complementary problems [J]. European Journal of Operational Research, 2004, 158: 409-417.
[15] 薛定宇, 陈阳泉. 高等应用数学问题的MATLAB求解[M]. 2版. 北京: 清华大学出版社, 2008: 165-184.
XUE Ding-yu, CHEN Yang-quan. Solving applied mathematical problems with MATLAB[M]. 2nd ed. Beijing: Tsinghua University Press, 2008: 165-184.
[16] 龚纯, 王正林. 精通MATLAB最优化计算[M]. 北京: 电子工业出版社, 2009: 78-217.
GONG Chun, WANG Zheng-lin. Proficient in MATLAB optimization calculation[M]. Beijing: Electronic Industry Press, 2009: 78-217.
[17] 李兴斯. 一类不可微优化问题的有效解法[J]. 中国科学A, 1994, 24(4): 371-377.
LI Xing-si. An efficient method for non-differentiable optimization problem[J]. Science in China Series A, 1994, 24(4): 371-337.
[18] Watson L T. Solving the nonlinear complementarity problem by a homotopy method [J]. SIAM Journal on Control and Optimization, 1979, 17: 36-46.
[19] Kojima M, Shindo S. Extensions of Newton and quasi-Newton methods to systems of PC equations [J]. Journal of Operations Research Society of Japan, 1986, 29: 352-374.
[20] Xia Y, Leung H, Wang J. A projection neural network and its application to constrained optimization problems [J]. IEEE Transactions on Circuits and Systems, 2002, 49: 447-458.
(编辑 龙怀中)
收稿日期：2011-04-15；修回日期：2011-06-15
基金项目：陕西省教育厅自然科学研究项目(09JK381)
通信作者：雍龙泉(1980-)，男，硕士，讲师，从事优化理论与算法设计及其应用研究；电话：13488458610；E-mail: yonglongquan@sohu.com
摘要：在非线性互补问题解存在的情况下，给出求解此类问题的一类新的算法。首先将非线性互补问题转化为多目标优化，给出多目标优化问题零有效解的定义；进而得到多目标优化问题的零有效解，即非线性互补问题的最优解，最后采用极大极小方法求解转化后的多目标优化问题。数值模拟结果表明该方法的正确性和有效性.
