J. Cent. South Univ. (2016) 23: 344-352
DOI: 10.1007/s11771-016-3079-z

Transient reliability optimization for turbine disk radial deformation
Fei Cheng-wei(费成巍)1, 2, Bai Guang-chen(白广忱)2, Tang Wen-zhong(唐文忠)3,
CHOY Yat-sze(蔡逸思)1, GAO Hai-feng(高海峰)2
1. Department of Mechanical Engineering, the Hong Kong Polytechnic University, Hong Kong, China;
2. School of Energy and Power Engineering, Beihang University, Beijing 100191, China;
3. School of Computer Science and Engineering, Beihang University, Beijing 100191, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract:
The radial deformation design of turbine disk seriously influences the control of gas turbine high pressure turbine (HPT) blade-tip radial running clearance (BTRRC). To improve the design of BTRRC under continuous operation, the nonlinear dynamic reliability optimization of disk radial deformation was implemented based on extremum response surface method (ERSM), including ERSM-based quadratic function (QF-ERSM) and ERSM-based support vector machine of regression (SR-ERSM). The mathematical models of the two methods were established and the framework of reliability-based dynamic design optimization was developed. The numerical experiments demonstrate that the proposed optimization methods have the promising potential in reducing additional design samples and improving computational efficiency with acceptable precision, in which the SR-ERSM emerges more obviously. Through the case study, we find that disk radial deformation is reduced by about 6.5×10–5 m; δ=1.31×10–3 m is optimal for turbine disk radial deformation design and the proposed methods are verified again. The presented efforts provide an effective optimization method for the nonlinear transient design of motion structures for further research, and enrich mechanical reliability design theory.
Key words:
1 Introduction
Blade-tip radial running clearance (BTRRC) impacts the performance and reliability of gas turbine so that the BTRRC has to be controlled to keep a reasonable clearance in all working conditions. In fact, of directly determining BTRRC variation under working conditions, the disk radial deformation is one important factor [1-4]. Hence, the optimal design of disk radial deformation is executed expectantly to keep a reasonable radial deformation subject to constraints on reliability and some other practical conditions. Along with the growth in computing power of current computers, expensive finite element (FE) method has become a common and important technique in the product development program. A large number of FE codes have been mainly applied to stress analysis, thermal analysis, vibration analysis, fatigue life estimates and design of gas turbine typical components [5-7]. The turbine disk bears vast mechanical and thermal loads under the working conditions with high temperature and high rotational velocity [8]. Thus, for the transient optimization design of turbine disk excessive computational cost and impractical runtime emerge by FE method.
One alternative is to construct a simple surrogate model (also called response surface method, RSM) to approximate the response of FE solvers [8]. The use of surrogate model often only requires a small number of FE analyses and therefore is able to significantly reduce the computational cost in reliability optimal design. Classic surrogate models for engineering design problems include polynomial-based response surface model, support vector machine (SVM) model, etc [9]. A polynomial-based response surface model is widely used due to its simplicity and effectiveness [10-12]. SVM is a kind of intelligent statistical learning method and is suitable for small sample [13]. Currently, SVM as an implicit performance function has been employed in reliability analysis and optimal design [14-15]. However, the two RSMs are not suitable for the nonlinear dynamic optimization analysis of complex structure because their response surface function can only approximate performance function around one design point [14]. Under the circumstances, the idea of extremum response surface method (ERSM) was proposed and the ERSM-based quadratic function (QF-ERSM) was developed for the reliability analysis of flexible robot manipulator [16], the nonlinear dynamic probabilistic design of aeroengine typical components [17] and mechanical dynamic assembly reliability analysis [18]. Meanwhile, the ERSM-based support vector machine of regression (SR-ERSM) has been presented for the nonlinear dynamic probabilistic analysis of turbine casing radial deformation [14]. However, no relative achievement on the ERSM in the application of structure optimization has been published so far.
The objective of the present work is to present two optimization methods of QF-ERSM and SR-ERSM to reduce computing time for reliability-based nonlinear dynamic design optimization. The presented methods are employed to the nonlinear dynamic multi-disciplinary reliability optimization of disk radial deformation with respect to nonlinear dynamic loads, such as thermal load and centrifugal force.
2 Extremum response surface method
In dynamic reliability analysis, the ERSM is used to consider a single extreme value as the response rather than a series of dynamic output responses under the different input vectors within a time domain [0, T], which is equivalent to transform a stochastic process of output response into a random variable [16-17]. The ERSM is promising to reduce computing cost and enhance calculation efficiency. With the jth group of input samples xj, the extremum of output response Yj(t, xj) is Yj,max(xj) within the time domain [0, T]. The data set {Yj,max(xj): j=1, 2, …, l} consisting of the maximum output responses is used to fit the extremum response curve Y(x):
 (1)
(1)
where f(x) is an extremum response surface function (ERSF); l is the total number of input samples.
ERSF is a key factor for dynamic reliability design because a valid ERSF is beneficial to directly enhance the efficiency and precision of reliability design. If the ERSF is applied to dynamic reliability optimization, the method is called the ERSM of reliability optimal design, which belongs to the global response surface method. This work is to introduce QF-ERSM and SR-ERSM.
2.1 Extremum response surface method-based quadratic function (QF-ERSM)
According to Ref. [16], the ERSF-based quadratic function(QF-ERSF) YQF(x) can be written as
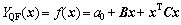 (2)
(2)
where B, C and x are determined by
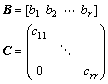
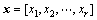
in which r is the number of random variables.
If the QF-ERSF is applied to the dynamic optimal design of complex machine replacing the FE model, this method is called QF-ERSM.
2.2 Extremum response surface method–based support vector machine of regression
This work takes the SR as an ERSF for nonlinear dynamic optimal design. For a certain kind of assumed distribution P(x, y) where x∈Rn and y∈R as well as the sampling points {(xi, yi)}i=1,2,…,l (l is the number of samples), when a set of functions maps a point in the space Rn onto the space R, i.e.
 (3)
(3)
where  is a set of parameters and ω is an undetermined parameter vector.
is a set of parameters and ω is an undetermined parameter vector.
The regression object of support vector machine is to find a function f∈F to make Eq. (4) have the lowest expected risk:
 (4)
(4)
where l(y-f(x, ω)) is an error function [15] and expressed as
 (5)
(5)
For the nonlinear regression, function f is calculated as follows.
Each sampling point is mapped onto higher dimensional space by a nonlinear function φ in order to conduct linear regression in the higher dimensional space, and then the original space nonlinear regression is attained. Thus, the function f is rewritten as
 (6)
(6)
From the above equation, the problem of solving the regression function is transformed to obtain the following optimal solution:
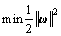 (7)
(7)
subject to
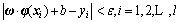 (8)
(8)
Considering the possible errors, two slack variables are introduced as  the optimization function is
the optimization function is
 (9)
(9)
 (10)
(10)
where γ is a penalty coefficient.
For obtaining the optimal solution, the Lagrange function is adopted by
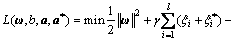
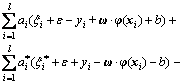
 (11)
(11)
where 
In the optimization process, a kernel function ψ(xi, xj) is applied to replacing the inner product <φ(xi), φ(xj)> in higher dimensional space, where the Lagrange duality problem is expressed by
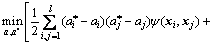
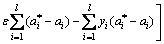 (12)
(12)
subjected to the constraints:
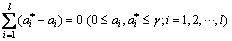 (13)
(13)
Therefore, the regression estimating function is
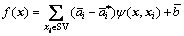 (14)
(14)
where SV is a set of support vectors for a given sample set;  and
and 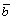 and the optimized solution in line with ERSM. the mathematical model of SR-ERSF YSR(x) is
and the optimized solution in line with ERSM. the mathematical model of SR-ERSF YSR(x) is
 (15)
(15)
Equation (15) is the SR-ERSF, where x and xi are
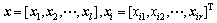
where i=1, 2, …, l; l is the number of sample values; r is the number of random variables.
Similarly, when the SR-ERSF is applied to the dynamic reliability design of complex machine replacing the FE model, this method is called SR-ERSM.
2.3 Optimization process based on ERSM
For structural reliability optimal design, it is difficult that the limit state function cannot be expressed by specific explicit form. To overcome this issue, the ERSM is employed to the reliability optimized design of disk radial deformation. The optimization design of complex structure needs many times loop computing (repeatedly analysis). The flow diagram of reliability optimization based on ERSM is shown in Fig. 1.
3 Optimization model of turbine disk radial deformation
3.1 Implementation of turbine disk radial deformation
An HPT of an aeroengine was selected in Fig. 2 to study the radial deformation of the disk. The disk structure is modeled as a rotating disk of uniform thickness. Considering the disk radial deformations due to both centrifugal load and thermal load, the simplified model δ(t) of disk radial deformation at time t [3] is
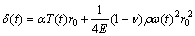 (16)
(16)
where δ(t), T(t) and ω(t) are the time-varying functions of disk’s radial deformation, surface temperature and rotor angular speed, respectively; α, ρ, v and E are the convection heat transfer coefficient, density, Poisson ratio and elastic modulus of the disk, respectively; r0 is the unstressed radius of the disk.
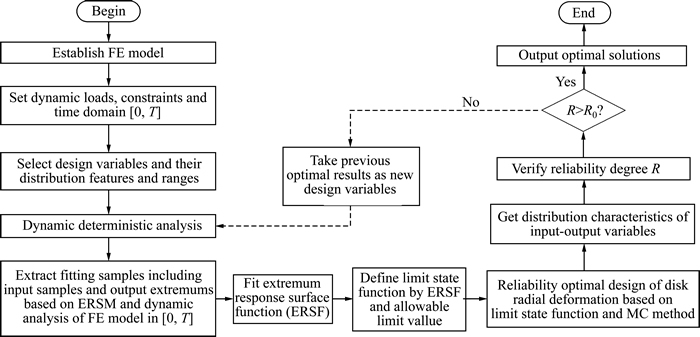
Fig. 1 Flowchart of reliability-based dynamic design optimization with ERSM
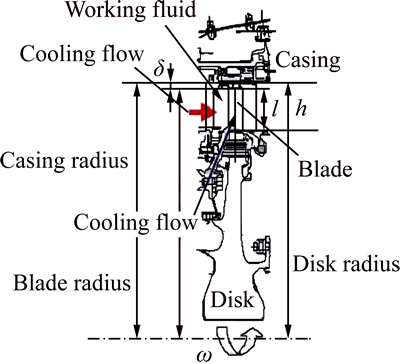
Fig. 2 Geometry configuration
3.2 Reliability calculation
For an aeroengine, the BTRRC changes inversely with the radial deformation of turbine disk. To ensure the safety of BTRRC, the disk radial deformation should be less than a maximum allowable value δmax. Therefore, the limit state functions of QF-ERSM and SR-ERSM are, respectively,
 (17)
(17)

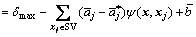 (18)
(18)
where H≥0 denotes the system secure while H≤0 indicates the failure of system. In the light of the limit state functions, the system during transient process is secure when the maximum radial deformation of turbine disk Y(x) is less than the maximum allowable value δmax. Hence, the ERSM can be employed to the reliability optimization of disk radial deformation. When μ=[μ1, μ2, …, μr], D=[D1, D2, …, Dr] and the random variables (x1, x2, …, xr) are mutually independent, H, x, μ and D meet
 (19)
(19)
when H obeys a normal distribution and its reliability index β and probability (reliability degree R) are represented by
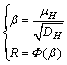 (20)
(20)
3.3 Optimization model
In order to weigh the performance and reliability of gas turbine, the disk radial deformation should potentially close to the allowable value δmax to keep an acceptable performance, subjected to a reasonable reliability degree R which should be large than a minimum value R0 [1]. Therefore, we consider the reliability degree R of disk radial deformation as the performance constraints to minimize the two limit state functions (Eqs. (17) and (18)), also called as the objective functions of disk radial deformation optimization. Hence, based on the mean value model of reliability optimization, the standard reliability optimization models of QF-ERSM and SR-ERSM can be formulated as follows:
 (21)
(21)
where x is design variables vector; a and b are the lower bound vector and upper bound vector of design variable vector x respectively, which are defined by the variable coefficient v and the mean value vector μ; μ0 and δ0 are the presupposed mean and standard deviation vectors, respectively; μ and δ are the mean and standard deviation vectors after optimization, respectively; Φ-1(·) is the inverse normal distribution function; R0 is the possible minimum reliability degree; g(X, t) is the equality constraint that the design variables should meet.
In Eq. (21), the correlative parameters (μ, d, g(x, t), R0) are denoted the random design variables x and then the repression of output response YSR(x) is gained based on these design variables in each iteration. In line with Monte Carlo method (MCM), the mean value μ and standard deviation d (d=vμ, v is the variable coefficient of design variables) of design variable vector are input into Eq. (21) to obtain the mean value model of reliability optimal design of structural response.
4 Numerical experiment
In this section, three nonlinear or/and dynamic numerical test functions are employed to assess the accuracy and efficiency of QF-ERSM and SR-ERSM in optimal design.
The first test problem, denoted by P1, is a mystery nonlinear function (Haupt function) [8], defined as
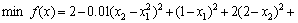
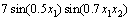 (22)
(22)
where x1, x2∈[0,5]. It has three local optimal solutions. One of them is the global solution with a value of -1.4565 as x*=(x1, x2)=(2.5044,2.5778).
The second test problem, denoted by P2, is a nonlinear dynamic function with semi-infinite and multi-variable constraints, defined as
 (23)
(23)
where the semi-infinite time-varying constraints Ki(x,t) (i=1,2; t∈[0, 100 s]) is
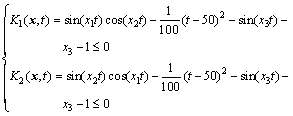 (24)
(24)
It has a optimal solution x*=(x1, x2, x3)=(4.2302, 5.0559, 1.5093) with a function value of 157.7923.
The third test problem, denoted by P3, is the nonlinear dynamic quadratic function defined as 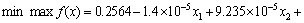
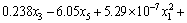
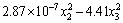
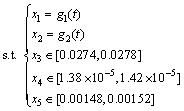 (25)
(25)
where t∈[0, 215 s], g1(t) and g2(t) are two time-varying functions. the curves of which are shown in Fig. 3. g1(t) and g2(t) reach the maximum values of 1168 and 1050 respectively at t=181.3 s. the function has a global solution at x*=(x1, x2, x3, x4, x5)=(1156.9, 1034, 0.0278, 1.4×10–5, 0.00152) with a optimal value 1.2925 at t=181.3 s.
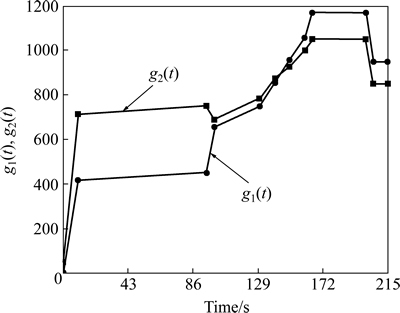
Fig. 3 Time-varying curves of g1(x) and g2(x)
Our optimization approaches were employed to fulfill the optimization of each problem. The comparison of results for QF-ERSM and SR-ERSM on the three test problems is listed in Table 1.
As shown in Table 1, the objective values obtained by two optimization methods are quite close for each test problem. All relative errors between objective values and theoretic optimal values are very small(less than 0.6%), namely, the optimization precision reaches 99.4%. Hence, the proposed QF-ERSM and SR-ERSM possess high computing accuracy for these problems. Furthermore, the number of needed samples, function evaluations, number of iterations and elapsed time for the SR-ERSM are far less than the QF-ERSM for the three test problems. Hence, the result indicates that the approximate optimization method ERSM is efficacious for the nonlinear dynamic optimal design with acceptable computational efficiency and accuracy; and the SR-ERSM has quite lower computational cost and higher efficiency.
Table 1 Comparison between results from QF-ERSM and SR-ERSM

5 Optimization design of turbine disk radial deformation
In this section, the optimization of the disk radial deformation is to be completed by using our proposed methods on an Intel Pentium 4 desktop computer (2.13 GHz CPU and 4 GB RAM).
5.1 Finite element (FE) model
The turbine disk is simplified as an axi-symmetric rotating disk with a centric bore. The circular cylindrical coordinates (r, h, z) are adopted for the convenience of description and analysis, where the symmetric axis z is consistent with the axial direction of the turbine disk. The half-axial cross section (FE model) of the turbine disk is shown in Fig. 4, where different areas of disk are defined as A1, A2, A3, B1, B2 and B3.

Fig. 4 Finite element model of turbine disk
5.2 Parameters selection
The radial deformation of disk is determined by many factors, including rotor speed w, disk surface temperature Tdisk, material properties (i.e. density ρ, thermal expansion coefficients k, thermal conductivity l), and convection heat transfer coefficients (α1, α2, α3, α4, α5 and α6) respectively corresponding to the locations of A1, A2, A3, B1, B2 and B3. The convection heat transfer coefficients on different locations in the disk are assumed to be different and nonlinear shown in Table 2. Meanwhile, the thermal expansion coefficient k and thermal conductivity l listed in Table 3 are also obviously nonlinear with the surface temperature of disk. In addition, the surface temperature of disk is predetermined by the compressor discharge temperature T, convection heat transfer coefficient and thermal conductivity [19]. Under aeroengine operation, the rotor speed w and the temperature T are dynamic with time (time-varying). Hence, the flight profile parameters (w and T) of load spectrums were selected from aeroengine [20] in Fig. 5. For the convenience of disk radial deformation reliability analysis, the maximum values of aforementioned nonlinear and dynamic parameters were selected as random variables according to the extremum selection method [21]. Therefore, the distribution characteristics of the aforementioned parameters are shown in Table 4, where the variable coefficient v is 0.03.
Table 2 Convection heat transfer coefficients of different locations on disk

Table 3 Heat conductivity and expansion coefficient under different temperature (reference 20 °C)
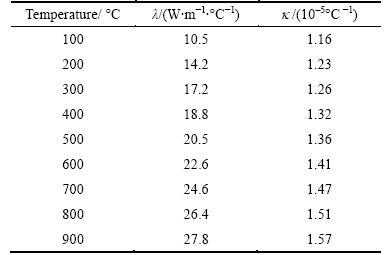

Fig. 5 Load spectra from aeroengine
5.3 Dynamic deterministic analysis
The dynamic deterministic analysis of disk radial deformation was fulfilled by importing the mean values of random variables in Table 4 into the FE model by the thermosetting coupling method. The time-varying radial deformation is gained in Fig. 6. The maximum disk radial deformation is obtained at t=187.8 s approximately at which the distributions for temperature and radial deformation on disk is shown in Fig. 7. Obviously, the temperature and radial deformation on the outside of disk reach the maximum, approximately 540 °C and 1.3693 mm, respectively, while the hub of turbine disk has low surface temperature and small radial deformation.
Table 4 Numerical characteristic of extremum random variables


Fig. 6 Variation of disk radial deformation (Y)
Note that the maximum of disk radial deformation determines whether the system is safe in [0, 215 s], because the limit state function is secure in whole analysis process when the extremum of disk radial deformation is less than the maximum deformation δmax in [0, 215 s]. Therefore, the ERSM is suitable for the reliability optimized design of disk radial deformation.
5.4 Fit and validate ERSFs
A small quantity of samples of each random variable in Table 4 were extracted by MCM, and afterwards input into the FE model of turbine disk to gain the corresponding extremum output response. In this process, we obtain many groups of samples (or called fitting samples) containing input samples and output samples, which are used to construct the SR-ERSF and QF-ERSF where the QF-ERSF is shown in Eq. (26). The number of required sample and the fitting time of QF-ERSF and SR-ERSF are listed in Table 5. And then, the QF-ERSF and SR-ERSF are tested by 200 groups of samples again. The analysis results are listed in Table 5.
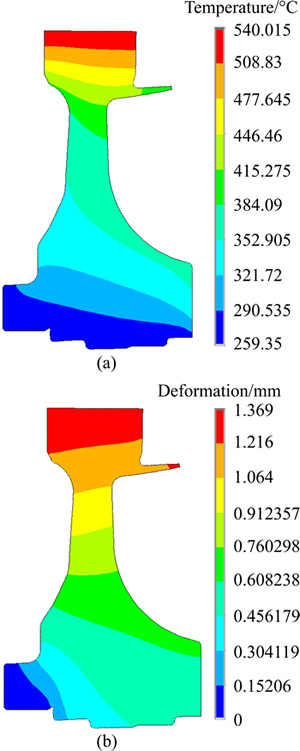
Fig. 7 Distribution of temperature (°C) (a) and (b) distribution of radial deformation
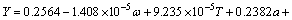
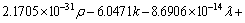
 (26)
(26)
Table 5 Optimization results of three methods (SR-ERSM, QF-ERSM and MCM)
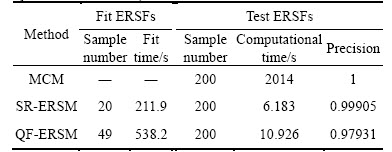
As listed in Table 5, fitting ERSFs (SR-ERSM) consumes fewer samples and less runtime than QF-ERSM. From the test results, the SR-ERSM saves 4.743 s in computing time and improves by 1.974% in precision relative to QF-ERSM. Thus, the SR-ERSM has higher computing efficiency and accuracy. Besides, the conclusions also validate the QF-ERSM and SR-ERSM with acceptable computational efficiency and accuracy.
5.5 Optimization design-based reliability degree for turbine disk radial deformation
Based on QF-ERSM and SR-ERSM, the reliability optimal design of disk radial deformation is enforced by each iteration with 10000 times simulations and the assumption of R0=0.99, δmax=1.31 mm, μ0=1.369 3×10–3 m and δ0=0 in the optimization model of disk radial deformation in Eq. (21). In the last time of iteration, the probabilistic distributions of disk radial deformation Y by QF-ERSM and SR-ERSM are shown in Fig. 8. From the optimization, the optimal solutions of QF-ERSM and SR-ERSM are x*=(1157.6, 526.9, 1836.1, 8210, 1.54×10–5, 27.92). The optimization results are listed in Table 6. The distributions of disk radial deformation after optimization with the two approaches are shown in Fig. 9.
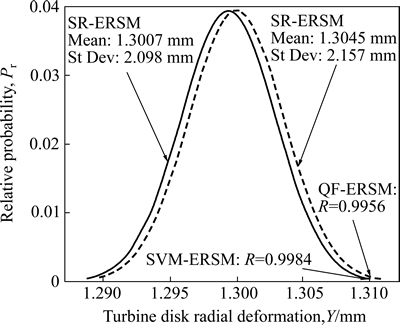
Fig. 8 Radical deformation distributions of extremum output response Y based on QF-ERSM and SR-ERSM
As shown in Figs. 8-9, the variation of disk radial deformation (or extremum output response) obeys a normal distribution with the means and standard deviations 1.3045 mm, 1.3007 mm and 2.157×10–5m, 2.098×10–5m, for QF-ERSM and SR-ERSM, respectively.
From Table 6, the disk radial deformation after optimization reduces at 6.48×10–5m and 6.86×10–5m for QF-ERSM and SR-ERSM under the reliability degree R>0.995 and the maximum permissible radial deformation δmax=1.31 mm. The results are promising to preferably control HPT blade-tip clearance and develop the performance and reliability of gas turbine. In addition, the computational efficiency and precision of the two proposed methods are acceptable. It is exciting that SR-ERSM is better due to less number of function evaluations and iterations, lower computational cost and higher efficiency. The results illustrate that the ERSM is a promising approach for the nonlinear dynamic optimization design of complex structure.

Fig. 9 Disk radial deformation distribution after optimization based on QF-ERSM (a) and SR-ERSM (b)
Table 6 Optimization results of disk radial deformation based on QF-ERSM and SR-ERSM

6 Conclusions
1) The ERSM is effective and feasible in improving culculation efficiency with an acceptable precision for nonlinear dynamic optimization.
2) These proposed methods (especially SR-ERSM) only require a small number of expensive FE analyses in the design optimization process so as to significantly reduce the total computational cost and run-time.
3) The desirable radial deformation and reasonable reliability of turbine disk are gained from the optimal design.
4) The SR-ERSF is a more accurate analysis model relative to the QF-ERSF.
5) This work provides a new research field for the transient deformation design of gas turbine components and even the control of HPT blade-tip clearance based on reliability optimization.
References
[1] LATTIME S B, STEINETZ B M. High pressure turbine clearance control system: current practices and future directions [J]. Journal of Propulsion and Power, 2004, 20: 302-311.
[2] ANNETTE E N, CHRISTIPH W M, STEPHAN S. Modeling and validation of the thermal effects on gas turbine transients [J]. Journal of Engineering for Gas Turbines and Power, 2005, 127: 564-572.
[3] BAI G C, FEI C W. Distributed collaborative response surface method for mechanical dynamic assembly reliability design [J]. Chinese Journal of Mechanical Engineering, 2013, 26: 1160-1168.
[4] HU D Y, WANG R Q, TAO Z. Probabilistic design for turbine disk at high temperature [J]. Aircraft Engineering and Aerospace Technology, 2011, 83: 199-207.
[5] ALDERSON R G, TANI M A, TREE D J. Three-dimensional optimization of a gas turbine disk and blade attachment [J]. Journal of Aircraft, 1976, 13: 994-999.
[6] MEGUID S A, KANTH P S, CZEJANSKI A. Finite element analysis of fir-tree region in turbine discs [J]. Finite Element Analysis Design, 2000, 35: 305-317.
[7] FARSHI B, JAHED H, MEHRABIAN A. Optimum design of inhomogeneous nonuniform rotating discs [J]. Computer and Structure, 2004, 82: 773-779.
[8] HUANG Z J, WANG C G, CHEN J. Optimal design of aeroengine turbine disc based on kriging surrogate models [J]. Computer and Structures, 2011, 89: 27-37.
[9] FORRESTER A I J, KEANE A J. Recent advances in surrogate-based optimization [J]. Progress of Aerospace Science, 2009, 45: 50-79.
[10] WANG G G. Adaptive response surface method using inherited Latin hypercube design points [J]. Journal of Mechanical Design, 2003, 125: 210-220.
[11] YENIAY O, UNAL R, LEPSCH R A. Using dual response surfaces to reduce variability in launch vehicle design: a case study [J]. Reliability Engineering System Safety, 2006, 91: 407-412.
[12] MURAT E K, HASAN B B, ALEMDAR B. Probabilistic nonlinear analysis of CFR dams by MCS using response surface method [J]. Applied Mathematical Modelling, 2011, 35: 2752-2770.
[13] FEI C W, BAI G C. Wavelet correlation feature scale entropy and fuzzy support vector machine approach for aeroengine whole-body vibration fault diagnosis [J]. Shock and Vibration, 2013, 20: 341-349.
[14] FEI C W, BAI G C. Nonlinear dynamic probabilistic analysis for turbine casing radial deformation using extremum response surface method based on support vector machine [J]. Journal of Computational and Nonlinear Dynamics, 2013, 8: 041004.
[15] GUO Z W, BAI G C. Application of least squares support vector machine for regression to reliability analysis [J]. Chinese Journal of Aeronautics, 2009, 22: 160-166.
[16] ZHANG C Y, BAI G C. Extremum response surface method of reliability analysis on two-link flexible robot manipulator [J]. Journal of Center South University, 2012, 19: 101-107.
[17] FEI C W, BAI G C. Extremum response surface method for casing radial deformation probabilistic analysis [J]. Journal of Aerospace Information System, 2013, 10: 58-63.
[18] FEI C W, BAI G C. Distributed collaborative extremum response surface method for mechanical dynamic assembly reliability analysis [J]. Journal of Central South University, 2013, 20: 2414-2422.
[19] KIM Y, METZGER D. Heat transfer and effectiveness on film cooled turbine blade tip models [J]. ASME Journal of Turbomachinery, 1995, 117: 12-21.
[20] KYPUROS J A, MELCHERK J. A reduced model for prediction of thermal and rotational effects on turbine tip clearance [R]. NASA/ TM-2003-212226, 2003.
[21] FEI C W, BAI G C. Extremum selection method of random variable for nonlinear dynamic reliability analysis of turbine blade deformation [J]. Propulsion and Power Research, 2012, 1: 58-63.
(Edited by YANG Hua)
Foundation item: Project(51275024) supported by the National Natural Science Foundations of China; Project(2015M580037) supported by China’s Postdoctoral Science Funding; Projects(XJ2015002, G-YZ90) supported by Hong Kong Scholars Program Foundations, China
Received date: 2014-12-09; Accepted date: 2015-04-20
Corresponding author: Tang Wen-zhong, professor, PhD; Tel: +86-10-82317418; E-mail: tangwenzhong@buaa.edu.cn
Abstract: The radial deformation design of turbine disk seriously influences the control of gas turbine high pressure turbine (HPT) blade-tip radial running clearance (BTRRC). To improve the design of BTRRC under continuous operation, the nonlinear dynamic reliability optimization of disk radial deformation was implemented based on extremum response surface method (ERSM), including ERSM-based quadratic function (QF-ERSM) and ERSM-based support vector machine of regression (SR-ERSM). The mathematical models of the two methods were established and the framework of reliability-based dynamic design optimization was developed. The numerical experiments demonstrate that the proposed optimization methods have the promising potential in reducing additional design samples and improving computational efficiency with acceptable precision, in which the SR-ERSM emerges more obviously. Through the case study, we find that disk radial deformation is reduced by about 6.5×10–5 m; δ=1.31×10–3 m is optimal for turbine disk radial deformation design and the proposed methods are verified again. The presented efforts provide an effective optimization method for the nonlinear transient design of motion structures for further research, and enrich mechanical reliability design theory.


