
ARTICLE
J. Cent. South Univ. (2019) 26: 1116-1132
DOI: https://doi.org/10.1007/s11771-019-4075-x
Effect of variable liquid properties on peristaltic transport of Rabinowitsch liquid in convectively heated complaint porous channel
Hanumesh VAIDYA1, Rajashekhar CHOUDHARI2,Manjunatha GUDEKOTE2, Kerehalli Vinayaka PRASAD3
1. Department of Mathematics, SSA Government First Grade College (Autonomous), Ballari, Karnataka, 583101, India;
2. Department of Mathematics, Manipal Institute of Technology, Manipal Academy of Higher Education, Manipal, Karnataka, 576104, India;
3. Department of Mathematics, Vijayanagara Srikrishnadevaraya University, Ballari, Karnataka,583105, India
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract:
The present paper emphasizes the peristaltic mechanism of Rabinowitsch liquid in a complaint porous channel under the influence of variable liquid properties and convective heat transfer. The effect of inclination on the complaint channel walls has been taken into account. The viscosity of the liquid varies across the thickness of the complaint channel, whereas, thermal conductivity varies concerning temperature. The nonlinear governing equations are solved by using perturbation technique under the long wavelength and small Reynold’s number approximations. The expressions for axial velocity, temperature, the coefficient of heat transfer and streamlines are obtained and analyzed graphically. The above said physiological phenomena are investigated for a specific set of relevant parameters on dilatant, Newtonian and pseudoplastic fluid models. The results presented here shows that the presence of variable viscosity, porous parameter and slip parameter significantly affects the flow quantities of dilatant, Newtonian and pseudoplastic fluid models. The investigation further reveals that an increase in the value of variable viscosity and porous parameters enhances the occurrence of trapping phenomenon. Moreover, the size of trapped bolus can be eliminated with suitably adjusting the angle of inclination parameter.
Key words:
Cite this article as:
Hanumesh VAIDYA, Rajashekhar CHOUDHARI, Manjunatha GUDEKOTE, Kerehalli Vinayaka PRASAD. Effect of variable liquid properties on peristaltic transport of Rabinowitsch liquid in convectively heated complaint porous channel [J]. Journal of Central South University, 2019, 26(5): 1116–1132.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-019-4075-x1 Introduction
The movement of biological liquids is by dynamic influxes of area contraction and expansion of the walls of the vessels. For example, in the development of the bolus through the throat, the movement of chyme in the gastrointestinal tract, the urine movement through the ureter and bloodstream in vessels prompts a peristaltic mechanism. This mechanism assumes a fundamental part in understanding numerous practical applications, such as in the heart-lung machine, dialysis machine, blood pump machine, development of poisonous liquid in atomic enterprises and the roller and finger pumps. Lately, the examinations on the peristaltic component through a porous medium in a channel/tube have gained an enormous enthusiasm in scientific research. The incorporation of a porous medium gives an additional favorable position in clarifying the complex rheological properties in various parts of the body, such as vascular beds, lungs, kidney and tumor vessels. Moreover, the stream of fluids through the porous medium with various geometries and designs has a ton of applications in the oil and plastic industry.
In particular, the developments of limestone, gallbladder, bile pipe, human lung, little veins are a portion of the primary instances of flow through porous media. Taking this fact into consideration, EL SHEHAWEY et al [1] studied peristaltic transport through a porous medium bounded by two porous plates. Later, NADEEM et al [2] extended the work done by EL SHEHAWEY et al [1] for linear Maxwell model. TRIPATHI [3] and ALSAEDI et al [4] investigated the peristaltic mechanism of couple-stress fluid through the porous medium. SANKAD et al [5] made use of couple stress fluid to examine the effects of the wall and slip on MHD peristaltic transport. SHIT et al [6] analyzed the results of slip velocity on peristaltic transport of couple stress fluid through an asymmetric non-uniform channel. Their investigation was found helpful in understanding the peristaltic mechanism involved in the digestive system. Recently, SIAVASHI et al [7] and MANJUNATHA et al [8] analyzed the classical and biological liquids flowing through porous structures.
The previously mentioned investigations do not consider the heat exchange outcomes on the peristaltic component of fluids coursing through the channel/tube. Despite, this idea assumes an essential part in understanding the physiological conduct of numerous biological systems [9]. The heat exchange in such systems typically happens in three distinct modes, namely, conduction, convection, and radiation. For the most part, the convective strategy for heat exchange assumes a critical role in the stream of blood through porous tissues, hemodialysis, coldness cryosurgery, oxygenation, and laser treatment. SRINIVAS et al [10] investigated the examination of mixed convective heat exchange on the peristaltic mechanism coursing through the vertical channel. The outcomes uncover the heat exchange coefficient increments with an expansion in the estimation of the Prandtl number. ABBASI et al [11] inspected the effect of convective limit conditions on the peristaltic component in a channel. The outcome demonstrates that expanding estimation of Biot number decreases the temperature profiles.As of late, a few scientists have considered the impact of boundary conditions on traditional fluids coursing through various geometries and suspicions [12–23].
Most of the examinations on peristalsis have been done by taking consistent thermophysical properties like variable thermal conductivity and variable viscosity. In any case, these properties may not be fundamental for isotropic liquids, but instead, they are the most imperative when the viscosity and temperature of the fluid continue changing, such as blood. Along these lines, in such conditions, it is essential to think about the variable viscosity and thermal conductivity into account. Roused by the utilization of variable viscosity, NADEEM et al [24] examined the effect of variable viscosity on peristaltic transport in an annulus. KHAN et al [25] investigated the impacts of slip and variable viscosity on peristaltic transport of non-Newtonian liquid in a channel. SINHA et al [26] explored the implications of slip and variable viscosity on MHD peristaltic transport in a channel. Their outcomes were discovered useful in controlling the velocity of blood by directing the magnetic field strength. Also, considering the variable thermal conductivity alongside variable viscosity has assembled the consideration of numerous specialists because of its vast significance in the field of medicine and industry. The investigations about the utilization of variable fluid properties have been recently reported in the Refs. [27–31].
Complaint walls can control the wave deformation. This compliance decides the adjustment in volume because of pressure and this impact in liquid stream issues can be identified with flexibility, firmness, and damping. Remembering these realities, HAYAT et al [32] broke down the MHD peristaltic system of a Jeffery liquid coursing through complaint permeable channel. Afterward, JAVED et al [33] utilized Burger’s fluid to depict the peristaltic component with the complaint walls. As of late, BHATTI et al [34], TANVEER et al [35] and HAYAT et al [36] examined the peristaltic transport of a Jeffery, Sisko and Williamson’s liquids in a complaint channel respectively.Inspired by the above examinations, the present investigation is carried out by utilizing the Rabinowitsch liquid to contemplate the peristaltic system. The Rabinowitsch model is one of the non-Newtonian models, which assumes a fundamental part in understanding the complex rheological properties of biological fluids. Its cubic stress model displays the characteristics of shear thinning or pseudoplastic (e.g., blood plasma, ketchup, and syrup), shear thickening or dilatant (e.g., sand, oobleck, and polyethylene glycol) and Newtonian (e.g., air and water) liquids [37–42].
To the best of author’s information, no undertaking has been made to examine the impacts of variable fluid properties and convective heat exchange on the peristaltic system of Rabinowitsch fluid in a complaint porous channel. The present investigation helps filling the gap toward this path. This examination helps understanding the rheological properties of bloodstream issues. Besides, the necessary components impacting the bloodstream in micro veins, i.e., variable viscosity, the variable thermal conductivity of the liquid, and convective, slip and compliance at the boundaries, are not omitted. Further, the impacts of relevant parameters on velocity, temperature, the coefficient of heat transfer and streamlines for dilatant, Newtonian and pseudoplastic liquid models are investigated and discussed through graphs.
2 Formulation of problem
Consider an incompressible viscous fluid flowing through a complaint porous channel inclined at an angle γ to the horizontal axis. The flow is governed by non-Newtonian Rabinowitsch fluid induced by the sinusoidal wave trains of wavelength λ. The variable viscosity and thermal conductivity of the fluid are taken into account. The channel walls are flexible in nature and are maintained at constant temperature T0.
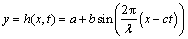 (1)
(1)
where a, b, x, c and t represent the radius of the channel, amplitude, axial direction, wave speed and time, respectively.
The two-dimensional governing equations for the flow field are given by
 (2)
(2)
 (3)
(3)
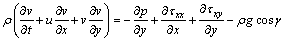 (4)
(4)
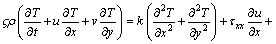
 (5)
(5)
where u and v are the velocity components in x and y directions, respectively; ρ denotes the density of the fluid; g denotes the acceleration due to gravity; p is the pressure; τxx, τxy, τyy are extra stress components; , T and k denote the specific heat at constant volume, temperature and thermal conductivity of the fluid, respectively.
, T and k denote the specific heat at constant volume, temperature and thermal conductivity of the fluid, respectively.
The constitutive equation of non-Newtonian Rabinowitsch model [41] is given by
 (6)
(6)
where α represents the coefficient of pseudoplasticity, which plays a significant role in differentiating the nature of the fluid and μ represents the fluid viscosity.
The equation of the flexible wall motion [41] is expressed as
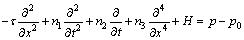 (7)
(7)
where τ, n1, n2, n3 and H denote the elastic tension in the membrane, the mass per unit area, the coefficient of the wall damping forces, the flexural rigidity of the plate and the spring stiffness, respectively.
For simplicity, the present investigation is carried out in half width of the channel. The continuity of stress implies that at the interface of the wall and fluid, the pressure is the same as that of the fluid at y=h. By considering the x component of momentum, Eq. (7) leads to
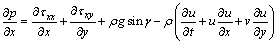 (8)
(8)
The non-dimensional quantities of interest are given below
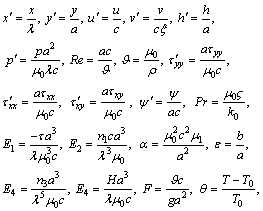
 (9)
(9)
Under the long wavelength and small Reynolds number approximation, Eqs. (2)–(6) after dropping the primes, take the form as given below
 (10)
(10)
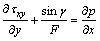 (11)
(11)
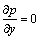 (12)
(12)
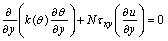 (13)
(13)
The corresponding non-dimensional boundary conditions are given by [43]
 (14)
(14)
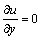 at y=0 (15)
at y=0 (15)
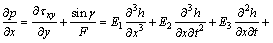
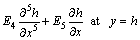 (16)
(16)
 (17)
(17)
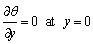 (18)
(18)
For small permeability, the boundary condition proposed by BEAVERS et al [44] was simplified by SAFFMAN [45] and is given in Eq. (14). Physically, this slip corresponds to the fact that there will be no momentum transfer from the fluid layer to the porous layer. Since the porous layer is completely saturated, the momentum instead of penetrating into a porous medium will be converted into drag by u. This u is the velocity of the fluid at the normal surface and is called the slip velocity (β) at the nominal surface.
The viscosity varies across the thickness of the channel walls and is given by
 (19)
(19)
where α1 is the coefficient of variable viscosity. The choice of α1 here is reasonable physiologically because a typical individual or creature of comparable size takes 1–2 L of fluid every day. Additionally, 6–7 L of fluid is gotten by the digestive tract as discharges from salivary organs, stomach, pancreas, liver, and the small digestive system itself. This incorporates the reliance of fluid concentration upon the radial axis, which influences the viscosity to diminish nearer to the vessel membrane.
The thermal conductivity varies with respect to temperature and is defined as below
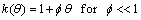 (20)
(20)
where f is the coefficient of thermal conductivity.
3 Solution of problem
Equations (10)–(12) are solved analytically with the help of boundary conditions (14)–(16), to get an expression for velocity;
 (21)
(21)
where 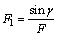 and
and
The stream function 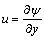 is obtained by integrating Eq. (21) with the help of boundary condition
is obtained by integrating Eq. (21) with the help of boundary condition 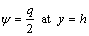 and then we obtain
and then we obtain
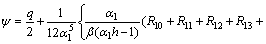
 (22)
(22)
The expression for temperature is solved with the help of perturbation technique to get an approximate solution for Eq. (13). However, the value of f is small in most of the practical problems, which enables us to utilize the perturbation solution.
The perturbed solution for Eq. (13) is obtained by expanding the series solution of the form given by [46]
 (23)
(23)
Zeroth order system:
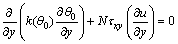 (24)
(24)
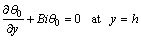 (25)
(25)
 (26)
(26)
First order system:
 (27)
(27)
 (28)
(28)
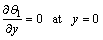 (29)
(29)
On solving zeroth and first order systems, the expression for temperature is obtained as

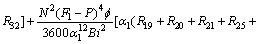
 (30)
(30)
The coefficient of heat transfer is given by
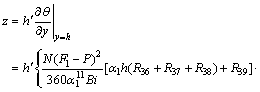
 (31)
(31)
where  .
.
4 Results and discussion
In this section, the impacts of variable viscosity (a1), porous parameter (Da), velocity slip parameter (β), the angle of inclination (γ), the wall tension parameter (E1), the mass characterization (E2), the wall damping parameter (E3), the rigidity parameter (E4), the wall elastic parameter (E5), variable thermal conductivity (f), Biot number (Bi), and Brinkmann number (Br) on velocity (u), temperature (θ), the coefficient of heat transfer (z) and streamlines (ψ) are analyzed and discussed through figures.
4.1 Validation of results
Figures 1–3 are plotted to compare the results of the present and SARAVANA et al [41] on velocity, temperature and the coefficient of heat transfer for dilatants, Newtonian and pseudoplastic liquid models. From the plots, the acquired outcomes are in concurrence with the results of Ref. [41]. Additionally, the consequences [41] can be gotten as a unique instance of the present model in the absence of variable liquid properties (α1=0 and f=0) and boundary conditions (Da=0 and Bi=0).
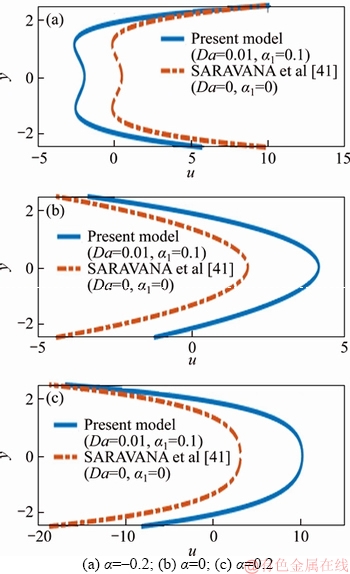
Figure 1 Comparison of velocity profiles with E1=0.1, E2= 0.04, E3=0.4, E4=0.002, E5=0.01, β=0.2, F=2, ε=0.6, γ=π/6, x=0.2, t=0.1:
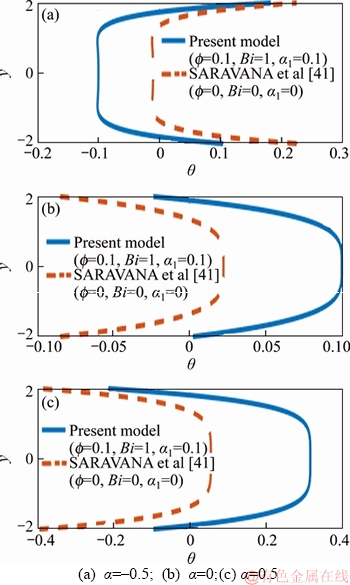
Figure 2 Comparison of temperature profiles with E1=0.1, E2= 0.04, E3=0.4, E4=0.002, E5=0.01, N=0.02, F=2, ε=0.6, γ=π/6, x=0.2, t=0.1:

Figure 3 Comparison of coefficient of heat transfer with E1=0.1, E2= 0.04, E3=0.4, E4=0.002, E5=0.01, N=0.02, F=2, ε=0.6, γ=π/6, t=0.1:
4.2 Velocity field
Figures 4–6 are designed to see the effects of relevant parameters on the velocity profiles.Figure 4 is the graph of the velocity profiles for expanding estimations of variable viscosity. It is seen from the figure that an expansion in the estimate of variable viscosity lessens the velocity profile for dilatant liquid, while it upgrades for Newtonian and pseudoplastic liquid models. This is because, for Newtonian and pseudoplastic fluid, a viscosity of the fluid tends to decrease with the flow speed and as a result, it enhances the velocity profiles. The effect of the porous parameter on the velocity profiles is represented in Figure 5. Here, the velocity profiles of shear thickening fluid declines for expanding estimations of the porous parameter; at the same time, inverse nature is seen on account of Newtonian and shear thinning liquids. Figure 6 is plotted to look at the impacts E1, E2, E3, E4 and E5 on velocity profiles. From the figure, the velocity profiles increase with an expansion in the estimation of E1 and E3, and it diminishes for expanding estimations of E2, E4 and E5 for shear thickening liquid. Whereas, for Newtonian and shear thinning fluids, the velocity profiles enhance for larger values of E1 and E2, but, it diminishes for an increase in E3, E4 and E5. It is because less resistance is accessible to the flow because of the wall properties and thus velocity increases for increasing values of E1 and E2. Further, the effects of velocity slip parameter and the angle of inclination parameter are tabulated in Table 1. From the table, an expansion in the estimation of velocity slip parameter upgrades the velocity profiles when α=–0.2, and it lessens when α=0 and 0.2. Also, it is noticed from the table that the velocity profiles of dilatant liquid declines with expanding estimations of the angle of inclination parameter. Besides, for Newtonian and pseudoplastic liquids, the velocity profiles upgrades for the more significant estimate of the angle of inclination parameter.

Figure 4 Velocity profiles for α1 with E1=0.1, E2=0.04, E3=0.4, E4=0.002, E5=0.01, t=0.1, Da=0.02, β=0.2, F=2, ε=0.6, γ=π/6, x=0.2, α=–0.2, 0, 0.2
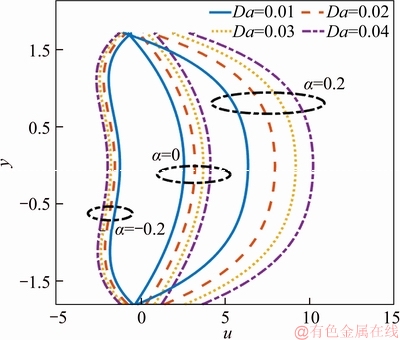
Figure 5 Velocity profiles for Da with E1=0.1, E2=0.04, E3=0.4, E4=0.002, E5=0.01, α1=0.1, β=0.2, F=2, ε=0.6, γ=π/6, x=0.2, t=0.1, α=–0.2, 0, 0.2

Figure 6 Velocity profiles for E1, E2, E3, E4 and E5 with F=2, α1=0.1, Da=0.02, γ=π/6, ε=0.6, β=0.2, x=0.2, t=0.1:
4.3 Temperature profiles
Figure 7 is plotted to examine the impact of variable thermal conductivity on temperature. The temperature profiles upgrade for all the three models (dilatant, Newtonian and pseudoplastic). This behavior is expected because an expansion in the estimation of thermal conductivity enables the liquid to disperse or retain the heat to its surroundings. Along these lines, when the temperature of the fluid is higher than the temperature of the boundary, an increase in thermal conductivity upgrades the temperature profiles. Figure 8 demonstrates the impacts of Biot number on temperature profiles. Generally, the temperature profiles of dilatant liquid enhance for higher estimations of Biot number, whereas it decreases for Newtonian and pseudoplastic fluids. This behavior is expected because an increase in the value of Biot number results in reducing the thermal conductivity of the fluid, which prompts the decrease of temperature for Newtonian and pseudoplastic liquids. Figure 9 depicts the effects of E1, E2, E3, E4 and E5 on temperature profiles. Here, temperature for all the three cases enhances for increasing values of E1 and E2, whereas, it reduces for a higher value of E3, E4 and E5. However, the effects of variable viscosity and Brinkmann number on temperature profiles are tabulated in Table 2.From the table, it is observed that higher estimations of variable viscosity decrease the temperature profiles of shear thickening liquid. However, inverse conduct is seen for Newtonian and shear thinning fluids. Furthermore, the impact of Brinkmann number on temperature reveals that, an increase in the value of Brinkmann number decreases the temperature profiles when α=–0.5. Also note that, when α=0 and 0.5, the temperature profiles enhance for higher values of Brinkmann number. This is a direct result of higher estimations of Brinkmann number improving the viscous dissipation impacts and henceforth building the temperature profiles.
Table 1 Values of velocity for different values of pertinent parameters
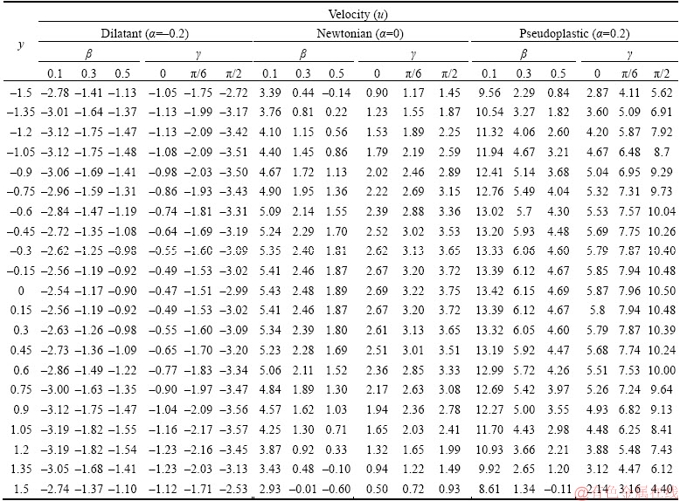
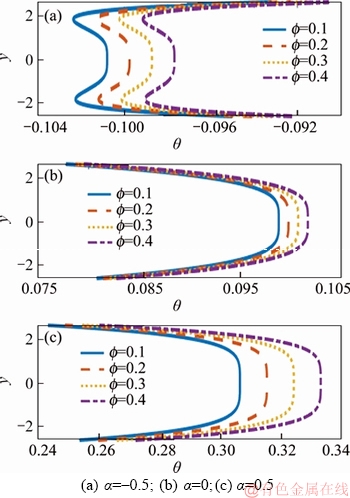
Figure 7 Temperature profiles for f with E1=0.1, E2=0.04, E3=0.4, E4=0.002, E5=0.01, α1=0.1, Bi=1, F=2, ε=0.6, γ=π/6, x=0.2, t=0.1, N=0.02:
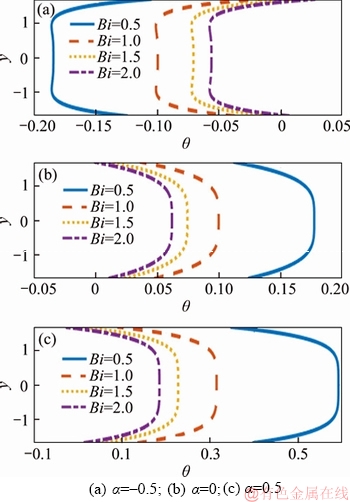
Figure 8 Temperature profiles for Bi with E1=0.1, E2=0.04, E3=0.4, E4=0.002, E5=0.01, f=0.1, F=2, ε=0.6, γ=π/6, x=0.2, t=0.1, N=0.02:

Figure 9 Temperature profiles for E1, E2, E3, E4 and E5 with F=2, f=0.1, γ=π/6, x=0.6, N=0.02, x=0.2, t=0.1, Bi=1:
Table 2 Values of temperature for different values of pertinent parameters

4.4 Coefficient of heat transfer
The impact of essential parameters on the coefficient of heat transfer is shown in Figures 10 and 11. Figure 10 is plotted to examine the effects of Brinkmann number on the coefficient of heat transfer. From the figure, it is noticed that, increasing values of Brinkmann number enhances the coefficient of heat transfer for dilatant, Newtonian and pseudoplastic fluid models. Further, the similar behavior is observed for the influence of variable viscosity and variable thermal conductivity on the coefficient of heat transfer for all the three considered fluid models (see Table 3). Figure 11 shows that an increase in the value of E1, E2 and E3 reduces the coefficient of heat transfer and it increases for E4 and E5 when α=–0.005. Furthermore, when α≥0, the coefficient of heat transfer enhances for E1, E2 and E3 and it diminishes for E4 and E5.

Figure 10 Coefficient of heat transfer for N with E1=0.1, E2=0.04, E3=0.4, E4=0.002, E5=0.01, α1=0.1, f=0.1, F=2, ε=0.6, γ=π/6, x=0.2, t=0.1, Bi=1:
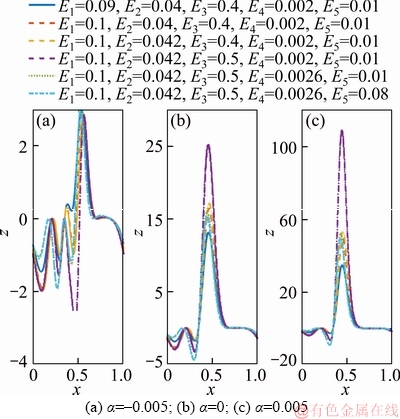
Figure 11 Coefficient of heat transfer for E1, E2, E3, E4 and E5 with F=2, α1=0.1, f=0.1, γ=π/6, ε=0.6, N=0.02, x=0.2, t=0.1, Bi=1:
4.5 Trapping phenomenon
Trapping phenomenon is an essential mechanism of peristaltic transport, where the development of bolus happens with the assistance of peristaltic wave. From Figures 12–14 it is discovered that the size of trapped bolus increases when the liquid changes from dilatant to pseudoplastic. Figures 12 and 13 uncover that an expansion in the estimation of variable viscosity and porous parameter enhances the size of the trapped bolus. Besides, the volume of trapped bolus can be controlled by altering the estimate of velocity slip parameter. Figure 15 illustrate the impact of E1, E2, E3, E4 and E5 on streamlines for pseudoplastic fluids. From the figure it is clear that the size of trapped bolus enhanced for higher values of E1, E2 and E3, whereas, it diminishes for E4 and E5. Furthermore, in all the above figures the formation of trapped bolus in Newtonian fluid increases compared to dilatant and pseudoplastic fluids.
5 Conclusions
The present investigation examines the effects of variable liquid properties and convective boundary conditions on the peristaltic component of Rabinowitsch liquid in a complaint porous channel.
The current study finds the application in designing the heart-lung machine, dialysis machine, etc. The investigation further gives a superior comprehension of the peristaltic system associated with the gastrointestinal tract and the stream of blood in small or microvessels. The principal findings from the present model are:
1) The consideration of variable viscosity and porous boundary reduces the velocity of dilatant fluid while it enhances for Newtonian and pseudoplastic fluids.
2) The presence of variable thermal conductivity enhances the temperature profiles for all the three cases.
3) The presence of convection conditions at the boundary diminishes the temperature profiles for Newtonian and pseudoplastic fluids.
4) Wall tension and mass characterization parameter increase the temperature, but wall damping, wall rigidity and wall elastic parameter decrease the temperature of shear thickening, Newtonian and shear thinning fluids.
5) The coefficient of heat transfer enhances for an increase in variable viscosity, variable thermal conductivity and Brinkmann number for α=–0.005, 0 and 0.005.
6) The volume of trapped bolus enhances when the liquid travels from dilatant to pseudoplastic.
Table 3 Values of coefficient of heat transfer for different values of pertinent parameters
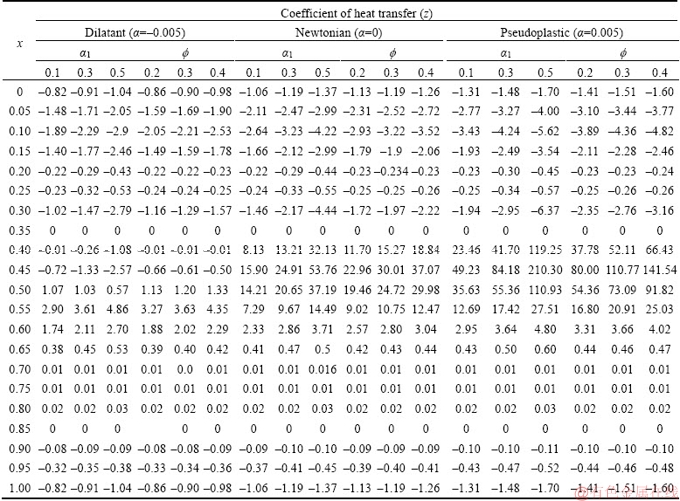

Figure 12 Streamlines with E1=0.1, E2=0.04, E3=0.4, E4=0.002, E5=0.01, Da=0.02, ε=0.6, γ=π/6, t=0.1, β=0.2, F=2, f=0.1:
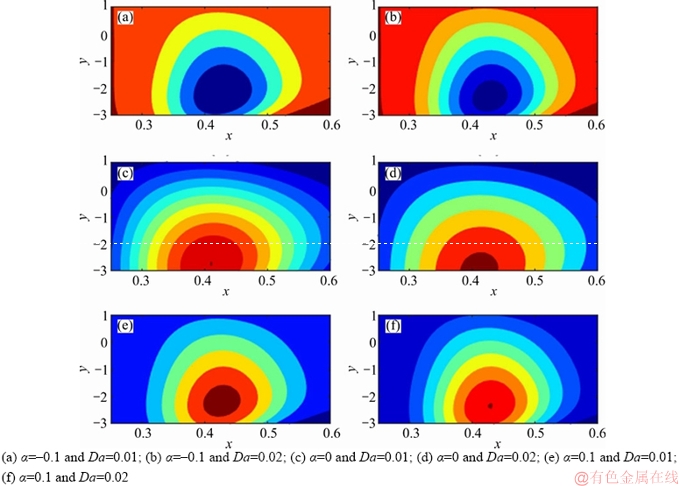
Figure 13 Streamlines E1=0.1, E2=0.04, E3=0.4, E4=0.002, E5=0.01, α1=0.1, ε=0.6, γ=π/6, t=0.1, β=0.2, F=2, f=0.1:

Figure 14 Streamlines E1=0.1, E2=0.04, E3=0.4, E4=0.002, E5=0.01, ε=0.6, γ=π/6, t=0.1, Da=0.02, F=2, f=0.1:

Figure 15 Streamlines with γ=π/6, t=0.1, α=0.1, F=2, f=0.1, Da=0.02, β=0.2, ε=0.6:
Nomenclature
G
Acceleration due to gravity
x, y
Axial and radial coordinates
Bi
Biot number
F
Body force parameter
Br
Brinkmann number
z
Coefficient of heat transfer
Da
Darcy number
Ec
Eckert number
E2
Mass characterization
Pr
Prandtl number
p
Pressure
a
Radius of the channel
Re
Reynolds number
E4
Rigidity parameter
k
Thermal conductivity
t
Time
u, v
Velocity components
E3
Wall damping parameter
E5
Wall elastic parameter
E1
Wall tension parameter
b
Wave amplitude
c
Wave speed
Greek letters
ε
Amplitude ratio
γ
Angle of inclination
α
Coefficient of pseudoplasticity
ρ
Density
τxx, τxy, τyy
Extra stress components
β
Velocity slip parameter

Specific heat at constant volume
ψ
Stream function
θ
Temperature
f
Variable thermal conductivity
α1
Variable viscosity
μ
Viscosity
λ
Wavelength
Acknowledgement
The authors appreciate the constructive comments of the reviewers which led to definite improvement in the paper.
Appendix
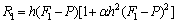



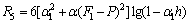

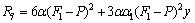







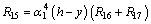

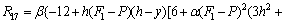
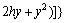



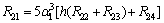
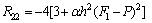




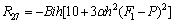
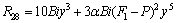
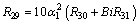





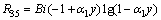
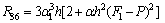


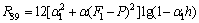
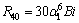

References
[1] EL SHEHAWEY E F, HUSSENY S Z A. Effect of porous boundaries on peristaltic transport through a porous medium [J]. Acta Mechanica, 2000, 143: 165–177. DOI: 10.1007/BF01170946.
[2] NADEEM S, AKRAM S. Peristaltic flow of a Maxwell model through porous boundaries in a porous medium [J]. Transport in Porous Media, 2011, 56: 895–909. DOI: 10.1007/s11242-010-9663-z.
[3] TRIPATHI D. Peristaltic hemodynamic flow of a couple-stress fluid through a porous medium with slip effect [J]. Transport in Porous Media, 2012, 92: 559–572. DOI: 10.1007/s11242-011-9920-9.
[4] ALSAEDI A, ALI N, TRIPATHI D, HAYAT T. Peristaltic flow of couple stress fluid through uniform porous medium [J]. Applied Mathematics and Mechanics, 2014, 35: 469–480. DOI: 10.1007/s10483-014-1805-8.
[5] SANKAD G C, NAGATHAN P S. Unsteady MHD peristaltic flow of a couple stress fluid through porous medium with wall and slip effects [J]. Alexandria Engineering Journal, 2016, 55: 2099–2105. DOI: 10.1016/j.aej.2016.06.029.
[6] SHIT G C, RANJIT N K. Role of velocity on peristaltic transport of couple stress fluid through an asymmetric non-uniform channel: Application to digestive system [J]. Journal of Molecular Liquid, 2016, 221: 305–315. DOI: 10.1016/j.molliq.2016.06.002.
[7] SIAVASHI M, RASAM H, IZADI A. Similarity solution of air and nanofluid impingement cooling of a cylindrical porous heat sink [J]. Journal of Thermal Analysis and Calorimetry, 2018, 135(2): 1399–1415. DOI: 10.1007/ s10973-018-7540-0.
[8] MANJUNATHA G, RAJASHEKHAR C. Slip effects on peristaltic transport of Casson fluid in an inclined elastic tube with porous walls [J]. Journal of Advanced Research in Fluid Mechanics and Thermal Sciences, 2018, 47: 201–208.
[9] RAMESH K. Influence of heat and mass transfer on peristaltic flow of a couple stress fluid through porous medium in the presence of inclined magnetic field in an inclined asymmetric channel [J]. Journal of Molecular Liquid, 2016, 219: 256–271. DOI: 10.1016/j.molliq.2016.03.010.
[10] SRINIVAS S, GAYATHRI R, KOTHANDAPANI M. Mixed convective heat and mass transfer in an asymmetric channel with peristalsis [J]. Communications in Nonlinear Science and Numerical Simulation, 2011, 16: 1845–1862. DOI: 10.1016/j.cnsns.2010.08.004.
[11] ABBASI F M, HAYAT T, AHMAD B. Peristaltic flow in an asymmetric channel with convective boundary conditions and Joule heating [J]. Journal Central South University, 2014, 21: 1411–1416. DOI: 10.1007/s11771-014-2079-0.
[12] HUSSAIN Q, ASGHAR S, HAYAT T, ALSAEDI A. Heat transfer in a porous saturated wavy channel with asymmetric convective boundary conditions [J]. Journal of Central South University, 2015, 22: 392–401. DOI: 10.1007/s11771-015- 2534-6.
[13] MEBAREK-OUDINA F, BESSAIH R. Oscillatory magnetohydrodynamic natural convection of liquid metal between vertical coaxial cylinders [J]. Journal of Applied Fluid Mechanics, 2016, 9: 1655–1665.
[14] SIAVASHI M, JAMALI M. Optimal selection of annulus radius ratio to enhance heat transfer with minimum entropy generation in developing laminar forced convection of water-Al2O3 nanofluid flow [J]. Journal of Central South University, 2017, 24: 1850–1865. DOI: 10.1007/s11771-017- 3593-7.
[15] SIAVASHI M, ROSTAMI A. Two-phase simulation of non-Newtonian nanofluid natural convection in a circular annulus partially or completely filled with porous media [J]. International Journal of Mechanical Sciences, 2017, 133: 689–703. DOI: 10.1016/j.ijmecsci.2017.09.031.
[16] OJJELA O, RAJU A, KAMBHATLA P K. Influence of thermophoresis and induced magnetic field on chemically reacting mixed convective flow of Jeffery fluid between porous parallel plates [J]. Journal of Molecular Liquid, 2017, 232: 195–206. DOI: 10.1016/j.molliq.2017.02.061.
[17] MEBAREK-OUDINA F. Numerical modelling of the hydrodynamic stability in vertical annulus with heat source of different lengths [J]. Engineering Science and Technology, an International Journal, 2017, 20: 1324–1333. DOI: 10.1016/j.jestch.2017.08.003.
[18] SIAVASHI M, KARIMI K, XIONG Q, DORANEHGARD M H. Numerical analysis of mixed convection of two-phase non-Newtonian nanofluid flow inside a partially porous square enclosure with a rotating cylinder [J]. Journal of Thermal Analysis and Calorimetry, 2018: 1–21. DOI: 10.1007/s10973-018-7945-9.
[19] WAKIF A, BOULAHIA Z, SEHAQUI R. A semianalytical analysis of electro-thermo-hydrodynamic stability in dielectric nanofluids using Buongiorno’s mathematical model together with more realistic boundary conditions [J]. Results in Physics, 2018, 9: 1438–1454. DOI: 10.1016/j.rinp.2018.01.066.
[20] WAKIF A, BOULAHIA Z, ALI F, EID M R, SEHAQUI R. Numerical analysis of the unsteady natural convection MHD Couette nanofluid flow in the presence of thermal radiation using single and two-phase nanofluid models for Cu-water nanofluids [J]. International Journal of Applied and Computational Mathematics, 2018, 4: 81. DOI: 10.1007/s40819-018-0513-y.
[21] WAKIF A, BOULAHIA Z, MISHRA S R, RASHIDI M M, SEHAQUI R. Influence of a uniform transverse magnetic field on the thermo-hydrodynamic stability in water-based nanofluids with metallic nanoparticles using the generalized Buongiorno’s mathematical model [J]. The European Physical Journal Plus, 2018, 133: 181. DOI: 10.1140/epjp/ i2018-12037-7.
[22] VAIDYA H, MANJUNATHA G, RAJASHEKHAR C, PRASAD K V. Role of slip and heat transfer on peristaltic transport of Herschel-Bulkley fluid through an elastic tube [J]. Multidiscipline Modeling in Materials and Structures, 2018, 14: 940–959. DOI: 10.1108/MMMS-11-2017-0144.
[23] MESBAH M, VATANI A, SIAVASHI M, DORANEHGARD M H. Parallel processing of numerical simulation of two-phase flow in fractured reservoirs considering the effect of natural flow barriers using the streamline simulation method [J]. International Journal of Heat and Mass Transfer, 2019, 131: 574–583. DOI:10.1016/ j.ijheatmasstransfer.2018.11.097.
[24] NADEEM S, AKBAR N S. Influence of heat transfer and variable viscosity in vertical porous annulus with peristalsis [J]. Journal of Porous Media, 2011, 14: 849–863. DOI: 10.1615/JPorMedia.v14.i10.20.
[25] KHAN A M, ELLAHI R, USMAN M. The effects of variable viscosity on the peristaltic flow of non-Newtonian fluid through porous medium in an inclined channel with slip boundary conditions [J]. Journal of Porous Media, 2013, 16: 59–67. DOI: 10.1016/j.aej.2015.03.030.
[26] SINHA A, SHIT G C, RANJIT N K. Peristaltic transport of MHD flow and heat transfer in an asymmetric channel: Effects of variable viscosity, velocity-slip and temperature jump [J]. Alexandria Engineering Journal, 2015, 54: 691– 704.
[27] VAJRAVELU K, PRASAD K V, CHIU-ON N G, VAIDYA H. MHD squeeze flow and heat transfer of a nanofluid between parallel disks with variable fluid properties and transpiration [J]. International Journal of Mechanical and Materials Engineering, 2019, 12: 9. DOI: 10.1186/s40712-017-0076-4.
[28] PRASAD K V, VAJRAVELU K, VAIDYA H, BASHA N Z, UMESH V. Thermal and species concentration of MHD Casson fluid at a vertical sheet in the presence of variable fluid properties [J]. Ain Shams Engineering Journal, 2018, 9: 1763–1779. DOI: 10.1016/j.asej.2016.08.017.
[29] PRASAD K V, VAIDYA H, VAJRAVELU K. MHD mixed convection heat transfer over a non-linear slender elastic sheet with variable fluid properties [J]. Applied Mathematics and Nonlinear Sciences, 2017, 2: 351–366. DOI: 10.21042/ AMNS.2017.2.00029.
[30] HAYAT T, FAROOQ S, AHMAD B, ALSAEDI A. Consequences of variable thermal conductivity and activation energy on peristalsis in curved configuration [J]. Journal of Molecular Liquid, 2018, 263: 258–267. DOI: 10.1016/j.molliq. 2018.04.109.
[31] RAJASHEKHAR C, MANJUNATHA G, VAIDYA H, DIVYA B B, PRASAD K V. Peristaltic flow of Casson liquid in an inclined porous tube with convective boundary conditions and variable liquid properties [J]. Frontiers in Heat and Mass Transfer, 2018, 11: 35.
[32] HAYAT T, JAVED M, ALI N. MHD peristaltic of a Jeffery fluid in a channel with compliant walls and porous space [J]. Transport in Porous Media, 2008, 74: 259–274. DOI: 10.1007/s11242-007-9196-2.
[33] JAVED M, HAYAT T, ALSAEDI A. Peristaltic flow of Burgers’ fluid with compliant walls and heat transfer [J]. Applied Mathematics and Computation, 2014, 244: 654–671. DOI: 10.1016/j.amc.2014.07.009.
[34] BHATTI M M, ELLAHI R, ZEESHAN A. Study of variable magnetic field on the peristaltic flow of Jeffery fluid in a non-uniform rectangular duct having compliant walls [J]. Journal of Molecular Liquid, 2016, 222: 101–108. DOI: 10.1016/j.molliq.2016.07.013.
[35] TANVEER A, HAYAT T, ALSAEDI A, AHMAD B. On modified Darcy’s law utilization in peristalsis of Sisko fluid [J]. Journal of Molecular Liquid, 2017, 236: 290–297. DOI: 10.1016/j.molliq.2017.04.041.
[36] HAYAT T, NAWAZ S, ALSAEDI A, RAFIQ M. Influence of radial magnetic field on the peristaltic flow of Williamson fluid in a curved complaint walls channel [J]. Results in Physics, 2017, 7: 982–990. DOI: 10.1016/j.rinp.2017.02.022.
[37] AKBAR N S, BUTT A W. Heat transfer analysis of Rabinowitsch fluid flow due to metachronal wave of cilia [J]. Results in Physics, 2015, 5: 92–98. DOI: 10.1016/j.rinp.2015.03.005.
[38] ALI N, SAJID M, JAVID K, AHMED R. Peristaltic flow of Rabinowitsch fluid in a curved channel: Mathematical analysis revisited [J]. Z Naturforsch, 2016, 72: 245–251. DOI: 10.1515/zna-2016-0334.
[39] SADAF H, NADEEM S. Analysis of combined convective and viscous dissipation effects for peristaltic flow Rabinowitsch fluid model [J]. Journal of Bionic Engineering, 2017, 14: 182–190. DOI: 10.1016/S1672-6529(16)60389-X.
[40] SINGH U P, MEDHAVI A, GUPTA R S, BHATT S S. Analysis of peristaltic of non-Newtonian fluids through nonuniform tubes: Rabinowitsch fluid model [J]. Z Naturforsch, 2017, 72: 601–608. DOI: 10.1515/zna-2017- 0033.
[41] SARAVANA R, VAJRAVELU K, SREENADH S. Influence of compliant walls and heat transfer on the peristaltic transport of a Rabinowitsch fluid in an inclined channel [J]. Z Naturforsch, 2018, 73: 833–842. DOI: 10.1515/zna-2018- 0181.
[42] VAIDYA H, RAJASHEKHAR C, MANJUNATHA G, PRASAD K V. Rheological properties and peristalsis of Rabinowitsch fluid through complaint porous walls in an inclined channel [J]. Journal of Nanofluids, 2019, 8: 970–979.
[43] AAMIR A, ASGHAR S, AWAIS A. Thermophoresis and concentration effects in a fourth grade peristaltic flow with convective walls [J]. Journal of Central South University, 2017, 24: 1654–1662. DOI: 10.1007/s11771-017-3571-0.
[44] BEAVERS G S, JOSEPH D D. Boundary conditions at a naturally permeable wall [J]. Journal of Fluid Mechanics, 1961, 30: 197–207. DOI: 10.1017/S0022112067001375.
[45] SAFFMAN P G. On the Boundary conditions at the surface of a porous medium, Studies in Applied Mathematics, 1971, 1: 93–101. DOI: 10.1002/sapm197150293.
[46] ZOLFAGHARIAN A, DARZI M, GHASEMI S E. Analysis of nano droplet dynamics with various sphericities using efficient computational techniques [J]. Journal of Central South University, 2017, 24: 2353–2359. DOI: 10.1007/ s11771-017-3647-x.
(Edited by YANG Hua)
中文导读
Rabinowitsch液的可变性对其在多孔通道中对流加热蠕动的影响
摘要:考虑液体性质的变化和对流换热的影响,研究了Rabinowitsch液在多孔通道中的蠕动机理。由于倾斜对通道壁的影响,液体的黏度沿通道厚度发生变化,而导热系数则随着温度的变化而变化。在长波长和小雷诺数近似的情况下,利用摄动法求解非线性控制方程,得到轴向速度、温度、热传递系数和流线的表达式并进行了图解分析。运用膨胀、牛顿和假塑性流体模型对上述现象进行了研究。结果表明,可变黏度、多孔参数和滑移参数对膨胀、牛顿和假塑性流体模型的流体流量有很大的影响。研究进一步揭示了由于可变黏度和多孔参数的增加而增强了俘获现象的发生。此外,可以通过适当调节倾斜角来调整所俘获的丸剂尺寸。
关键词:Rabinowitsch液;Biot数;孔参数;热导率;可变黏度;速度滑移
Received date: 2018-10-21; Accepted date: 2018-12-11
Corresponding author: Manjunatha GUDEKOTE, PhD, Professor; Tel: +91-9448728764; E-mail:gudekote_m@rediffmail.com; ORCID: 0000-0001-5347-753X
Abstract: The present paper emphasizes the peristaltic mechanism of Rabinowitsch liquid in a complaint porous channel under the influence of variable liquid properties and convective heat transfer. The effect of inclination on the complaint channel walls has been taken into account. The viscosity of the liquid varies across the thickness of the complaint channel, whereas, thermal conductivity varies concerning temperature. The nonlinear governing equations are solved by using perturbation technique under the long wavelength and small Reynold’s number approximations. The expressions for axial velocity, temperature, the coefficient of heat transfer and streamlines are obtained and analyzed graphically. The above said physiological phenomena are investigated for a specific set of relevant parameters on dilatant, Newtonian and pseudoplastic fluid models. The results presented here shows that the presence of variable viscosity, porous parameter and slip parameter significantly affects the flow quantities of dilatant, Newtonian and pseudoplastic fluid models. The investigation further reveals that an increase in the value of variable viscosity and porous parameters enhances the occurrence of trapping phenomenon. Moreover, the size of trapped bolus can be eliminated with suitably adjusting the angle of inclination parameter.


