Relationship between mechanical properties and grain size of AZ80 at 350 ?C under different strain rates
QUAN Guo-zheng(权国政), SONG Tao(宋涛), ZHOU Yi-jun(周一俊), WANG Feng-biao(王凤彪), ZHOU Jie(周杰)
College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China
Received 23 September 2009; accepted 30 January 2010
Abstract:
The dynamic recrystallization refinement of magnesium alloy AZ80 by compression tests was studied, and its effect on the mechanical properties was investigated. It is observed that the microstructure of the as-cast billet with grain size of 240 ?m becomes refined to about 120, 110, 94 and 50 ?m after upsetting at 350 ?C under strain rates of 0.01, 0.1, 1 and 10 s-1 respectively. The changes in the mechanical properties according to grain size show that yield strength significantly decreases with grain size increasing, while strain hardening exponent and micro hardness increase very sharply. Further, the grain size vs strain rate and change in Vickers micro hardness according to the various strain rates show that grain size and micro hardness decrease with strain rate increasing.
Key words:
magnesium alloy; refinement; compression; softening behaviour; micro hardness;
1 Introduction
At present, hot pressure forming is regarded as one of the most important processes to manufacture products with good mechanical properties and fine metallurgical structures. Considerable investigations have been done in order to establish flow stress relationships of materials during hot deformation based on the experimental results and great progress has been made[1]. Therefore, the equation for flow stress is numerically analyzed in order to promote the practical application of wrought magnesium alloys. Most of the constitutive equations for magnesium alloys are based on the compression deformation[2-6]. The mechanical properties of the workpiece under hot working are generally expressed by a constitutive equation, which connects flow stress and the variables such as strain, strain rate and temperature [7].
During hot forming the material is liable to undergo recrystallization, i.e. dynamic recrystallization that affects the crystallographic texture and thus, material anisotropy. Hence, it is of great importance to reveal the texture forming mechanisms during hot working with concurrent recrystallization since most commercial wrought Mg alloys are fabricated to semi-finished products by such processing. Recrystallization is understood to proceed by nucleation of strain free grains and their subsequent growth until complete impingement. Dynamic recrystallization in magnesium and its alloys has been reported to occur by several mechanisms. Those recrystallization mechanisms can be divided, according to the nature of the recrystallization process, into two groups: continuous and discontinuous recrystallization. Although this mechanism of forming new grains is considered by many researchers[8-13] as a recrystallization mechanism, it is stressed that the very nature of this mechanism is a strong recovery process rather than a classical recrystallization phenomenon, also referred to as discontinuous recrystallization characterized by nucleation and nucleus growth by high angle boundary migration.
Although the recrystallization mechanism is considered worldwide, this work that is focused on the relationship description for mechanical properties vs grain size is the latest. In the present work, compression tests were also carried out to investigate the effect of grain refinement on the mechanical properties such as yield strength, strain hardening exponent and micro hardness at 350 ?C under strain rates of 0.01, 0.1, 1 and 10 s-1. Meanwhile, the effect of the processing conditions such as strain rates on the grain refinement during compression experiments was investigated.
2 Experimental
The chemical composition of AZ80 magnesium alloy used in this study was (mass fraction, %) Al 8.90, Zn 0.53, Mn 0.20, Si 0.008, Fe 0.004, Cu 0.008, Ni 0.000 8, Mg balance. A computer-controlled, servo- hydraulic Gleeble 1500 machine was used for compression testing. It can be programmed to simulate both thermal and mechanical industrial process variables for a wide range of hot deformation conditions. The specimens were resistance heated at a heating rate of 1 ?C/s and held at 350 ?C for 180 s by thermocoupled- feedback-controlled AC current, which could decrease the anisotropy in flow deformation behavior effectively. So, the influence of compression direction on the deformation behavior was not considered in the present study. The homogenized ingot was scalped to diameter of 10 mm and height of 12 mm with grooves on both sides filled with machine oil mingled with graphite powder as lubrication to reduce friction between the anvils and specimen during isothermal hot compression tests with the total height reduction of 60% in 350 ?C at strain rates of 0.01, 0.1, 1 and 10 s-1.
The variations of stress and strain were monitored continuously by a personal computer equipped with an automatic data acquisition system. During the tests, the temperatures of the specimens were controlled to within ±0.1 ?C through three thermocouples adhibited with the specimens at the gauge zero. The true stress and true strain were derived from the measurement of the nominal stress-strain relationship according to the following formula: σt=σn(1+εn), εt= ln(1+εn), where σt is the true stress, σn is the nominal strain, εt is the true strain and εn is the nominal strain[4].
3 Results and discussion
3.1 Stress-strain behavior
The true compressive stress—strain curves of AZ80 alloy deformed at 350 ?C under four strain rates are shown in Fig.1. The flow stress as well as the shape of the flow curves is sensitively dependent on strain rate. For all of specimens, after initial yielding, the flow stress decreases monotonically with different softening rates due to the initiation of dynamic recrystallization. By comparing these curves with one another, it is found that, for a specific temperature, the flow stress decreases markedly with strain rate. Further, changes in strain rate have a significant effect on the dynamic softening rate. The degree of dynamic softening is considerably smaller during deformation at 350 ?C under lower strain rates of 0.01 s-1 and 0.1 s-1, with a nearly horizontal line obtained, suggesting that the rate of thermal softening is balanced by the rate of work-hardening. In contrast, for a fixed temperature, the flow stress generally increases as the strain rate increases due to an increase of dislocation density and the dislocation multiplication rate.
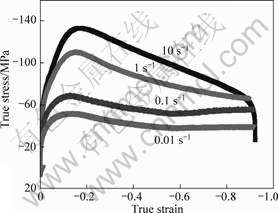
Fig.1 True stress—strain curves of AZ80 magnesium alloy obtained by thermal simulation
3.2 Strain hardening and strain rate sensitivity
In order to understand the plastic behaviour of AZ80 magnesium alloy at 350 ?C, the flow stress curves were analyzed by Fields-Backofen equation[14-16], which is the common formula for most metal materials:
(1)
where σ is the flow stress, ε is the strain, n is the strain hardening exponent, 
is the strain rate, m is the strain rate sensitivity exponent. This equation is the most common formula to describe the stress-strain relationship and it can well express the work-hardening phenomenon by the strain hardening exponent (n-value) and the strain rate sensitivity exponent (m-value), which are important parameters to influence the filling ability of metal.
According to Eq.(1), the following equation can be obtained:
(2)
1) Calculation of n-value
From the relationship between true stress and true strain in double logarithmic scale at a certain temperature and a certain strain rate, it can be seen that the values of stress under the uniform deformation stage are almost on the same line, in which the slope is equal to the value of strain hardening exponent. So, the slopes corresponding with the different strain rates can be obtained as 0.333, 0.335, 0.349 and 0.375. The mean value 0.348 of these slopes is accepted as n-value.
2) Calculation of m-value
It is assumed that the value of ln C+nln ε at a certain temperature under a certain strain is a constant of K1. The following formula can be obtained from Eq.(2):
(3)
Then, 
The linear relationships between ln σ and 
are fitted out, and the result of m-value is obtained as 0.115 3.
3.3 Grain refinement
Fig.2 shows the optical photographs illustrating the
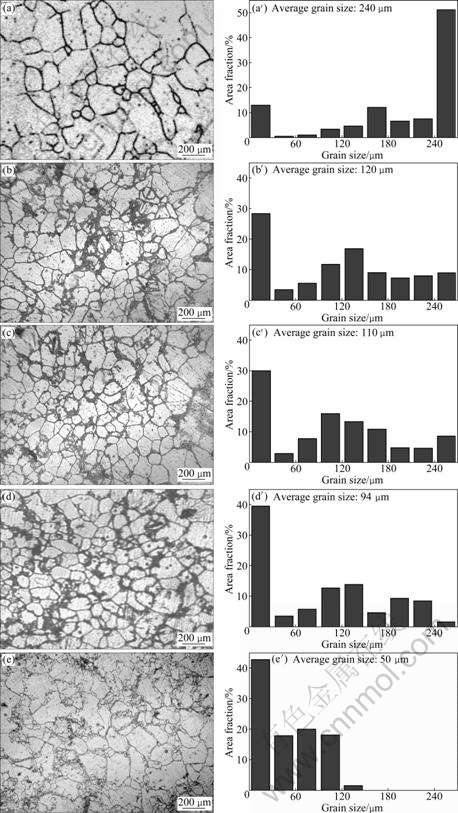
Fig.2 Optical photographs showing microstructural change and grain size distributions at 350 ?C under different strain rates: (a) As- received; (b) 0.01 s-1; (c) 0.1 s-1; (d) 1 s-1; (e) 10 s-1
grain refinement processes and grain size distributions at 350 ?C under different strain rates. As depicted, the microstructure of the as-cast billet with grain size (d) of 240 ?m becomes refined up to about 120 ?m after upsetting under strain rate of 0.01 s-1, to about 110 ?m under strain rate of 0.1 s-1, to about 94 ?m under strain rate of 1 s-1, to about 50 ?m under strain rate of 10 s-1. It can be seen that area fraction of large grains greater than 240 ?m after upsetting gets smaller to 10%, 9%, 2% and 0%. On the other hand, the area fraction of 12.6% of the finer grain less than 30 ?m after upsetting is increased up to 28%, 30%, 39% and 43%.
3.4 Mechanical properties vs grain size
Mechanical properties of compressed AZ80 such as yield strength, strain hardening exponent (n-value), and Vickers micro hardness were investigated using upsetting tests at temperatures of 350 ?C and strain rate of 0.01, 0.1, 1 and 10 s-1. Changes in the mechanical properties according to grain size are shown in Fig.3. As shown in Figs.3(a) and (b), the yield strength significantly decrease with grain size increasing, while strain hardening exponent increases very sharply.
It is worthy noting that opposite tendency between the strength and hardness takes place in terms of grain size. Fig.3(c) shows that micro hardness increases as the grain size increases. This may be due to the difference between the local deformation in micro hardness testing and macro deformation in compression testing. That is, locally increased dislocation density or the number of mechanical twinnings leads to the hardening of the material during the micro hardness testing. On the other hand, softening effect is more predominant owing to the grain refinement by dynamic recrystallization during the compression testing[17-18].
Fig.4 shows that the grain size vs strain rate and change in Vickers micro hardness according to the various strain rates. As can be seen in Fig.4(a), as the strain rate increases, the grain size decreases. Similarly, the micro hardness decreases with strain rate increasing, as shown in Fig.4(b).
4 Conclusions
1) It is observed that the microstructure of the as-cast billet with grain size of 240 ?m becomes refined to about 120, 110, 94 and 50 ?m after upsetting at 350 ?C under strain rates of 0.01, 0.1, 1 and 10 s-1, respectively.
Fig.3 Changes in yield strength (a), strain hardening exponent (n-value) (b), Vickers micro hardness (c) according to various strain rates at constant temperature of 350?C
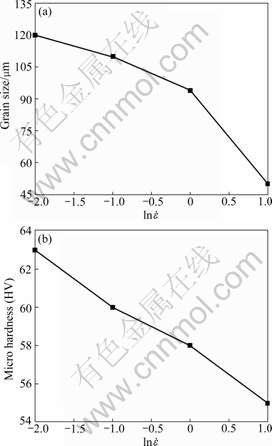
Fig.4 Changes in grain size (a) and micro hardness (b) at various strain rates
2) The changes in the mechanical properties according to grain size show that yield strength significantly decreases with grain size increasing, while strain hardening exponent and micro hardness increases very sharply.
3) The grain size vs. strain rate and change in Vickers micro hardness according to the various strain rates show that grain size and micro hardness decrease with strain rate increasing.
References
[1] HE Xiao-ming, YU Zhong-qi, LAI Xin-min. A method to predict flow stress considering dynamic recrystallization during hot deformation [J]. Computational Materials Science, 2008, 44(2): 760-764.
[2] LIU Juan, CUI Zhen-shan, LI Cong-xing. Modelling of flow stress characterizing dynamic recrystallization for magnesium alloy AZ31B [J]. Computational Materials Science, 2008, 41(3): 375-382.
[3] BARNETT M R. Influence of deformation conditions and texture on the high temperature flow stress of magnesium AZ31 [J]. Journal of Light Metals, 2001, 1(3): 167-177.
[4] CHENG Yong-qi, ZHANG Hui, CHEN Zhen-hua, XIAN Kui-feng. Flow stress equation of AZ31 magnesium alloy sheet during warm tensile deformation [J]. Journal of Materials Processing Technology, 2008, 208(1/3): 29-34.
[5] YANG Y Q, LI B C, ZHANG Z M. Flow stress of wrought magnesium alloys during hot compression deformation at medium and high temperatures [J]. Materials Science and Engineering A, 2009, 499(1/2): 238-241.
[6] TAKUDA H, MORISHITA T, KINOSHITA T, SHIRAKAWA N. Modelling of formula for flow stress of a magnesium alloy AZ31 sheet at elevated temperatures [J]. Journal of Materials Processing Technology, 2005, 164(5): 1258-1262.
[7] ZENG Z P, JONSSON S, ROVEN H J, ZHANG Y S. Modeling the flow stress for single peak dynamic recrystallization [J]. Materials and Design, 2009, 30(6): 1939-1943.
[8] ALSAMMAN T, GOTTSTEIN G. Dynamic recrystallization during high temperature deformation of magnesium [J]. Materials Science and Engineering A, 2008, 490(1/2): 411-420.
[9] SAKAI T, JONAS J J. Dynamic recrystallization: Mechanical and microstructural considerations [J]. Acta Metal., 1984, 32(2): 189--209.
[10] TAN J C, TAN M J. Dynamic continuous recrystallization characteristics in two stage deformation of Mg3Al1Zn alloy sheet [J]. Materials Science and Engineering A, 2003, 339(1/2): 124-132.
[11] YANG X Y, JI Z S, MIURA H, SAKAI T. Dynamic recrystallization and texture development during hot deformation of magnesium alloy AZ31 [J]. Transactions of Nonferrous Metals Society of China, 2009, 19(1): 55-60.
[12] FATEMI-VARZANEH S M, ZAREI-HANZAKI A, BELADI H. Dynamic recrystallization in AZ31 magnesium alloy [J]. Materials Science and Engineering A, 2007, 456(1/2): 52-57.
[13] GALIYEV A, R KAIBYSHEV R, GOTTSTEIN G. Correlation of plastic deformation and dynamic recrystallization in magnesium alloy ZK60 [J]. Acta Materialia, 2001, 49(7): 1199-1207.
[14] FIELDS D S, BACKOFEN W A. Determination of strain hardening characteristics by torsion testing [J]. Proceedings-American Society of Testing Materials, 1957, 57: 1259-1272.
[15] ZHOU M,CLODE M P. Constitutive equations for model in flow softening due to dynamic recovery and heat generation during plastic deformation [J]. Mechanics of Materials, 1998, 27(2): 63-76.
[16] GRONOSTAJSKI Z. The constitutive equations for FEM analysis [J]. Journal of Materials Processing Technology, 2000, 106(1/3): 40-44.
[17] CHOI S H, KIM J K, KIM B J, PARK Y B. The effect of grain size distribution on the shape of flow stress curves of Mg-3Al-1Zn under uniaxial compression [J]. Materials Science and Engineering A, 2008, 488(1/2): 458-467.
[18] KANG S H, LEE Y S, LEE J H. Effect of grain refinement of magnesium alloy AZ31 by severe plastic deformation on material characteristics [J]. Journal of Materials Processing Technology, 2008, 201(1/3): 436-440.
Foundation item: Project(cstc2009aa3012-1) supported by Science and Technology Committee of Chongqing, China; Project(20100470813) supported by China Postdoctoral Science Foundation; Project(2010011511) supported by Sharing Fund of Chongqing University’s Large-Scale Equipment, China
Corresponding author: QUAN Guo-zheng; Tel: +86-23-65103065; E-mail: quangz2005@yahoo.com.cn
