J. Cent. South Univ. (2012) 19: 465-470
DOI: 10.1007/s11771-012-1026-1![]()
MSMSE-based optimal beamforming design and simplification on AF MIMO two-way relay channels
WANG Zi-bin(王梓斌), XIANG Liang-jun(向良军), ZHENG Lin-hua(郑林华), DING Hong(丁宏)
School of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract:
An optimal cooperative beamforming for the amplify-and-forward (AF) MIMO two-way relay channels was designed. Supposing the channel state information (CSI) was perfectly known by the receiver and transmitter as well as the relay, optimal beamforming vectors (matrices) of all nodes were jointly designed based on the criterion of minimizing the sum mean square errors (MSMSE). The analysis result shows that the performance effect of transmitting and receiving beamforming pairs is to maximize the receive signal-to-noise ratio (SNR) at two communication nodes, and the rank of the optimal relay beamforming matrix is no larger than two when there is only one data stream at each source node. A simplified algorithm was put forward to accomplish the design based on the analysis conclusions. Simulation results provide that the system performance, which is characterized in terms of bit error rates (BER), is significantly improved by cooperative beamforming, and the performance of the simplified method is not only very close to the optimal one but also with faster iteration speed and much lower computational complexity.
Key words:
beamforming; two-way relay channels; amplify-and-forward; multiple input multiple output;
1 Introduction
Two-way relay communications have attracted significant attentions due to its increased spectral efficiency over one way relay communications. Among many existing protocols, amplify-and-forward (AF) is the simplest to implement [1]. In AF two-way relay communications exploiting the time division duplex (TDD), during the first time slot, also known as the multiple access (MAC) phase, two source nodes transmit their messages to the relay node simultaneously. In the second time slot, also named broadcast (BC) phase, the relay broadcasts its processed message to both source nodes. Since both source nodes know the message they transmitted to each other, self-interference (SI) can be cancelled in their received signal. Many works had been done on the capacity maximization [2-3] or system performance optimization [4-6] of two-way relay channel (TWRC). Recently, multiple antenna techniques were introduced to the TWRC [7-8]. With multiple input multiple output (MIMO) techniques, the channel capacity and the bit error rate (BER) performance of TWRCs can be greatly improved [9-10].
In addition to many works of the beamforming design on the one-way relay channel [11-12], transmitting beamforming or pre-equalizer was studied in Ref. [13] for TWRC. Optimal relay beamforming with analog network coding for TWRC was studied in Ref. [14], where some general conclusions on the relay beamforming matrix were also given, but only the single antenna source node was considered. In Ref. [15], instead of jointly designing the beamforming parameters, transmitting beamforming was designed first, and then, relay beamforming matrix based on zero-forcing (ZF) and minimum mean squared error (MMSE) criterion were designed, respectively. Inspired by Ref. [16], where the beamforming in typical MIMO channel was studied and a closed form solution of transmitting and receiving beamforming matrices were given, joint design of the receiving and relay beamforming were studied in Refs. [17-18] by minimizing the sum mean squared errors (MSMSE) and maximizing the sum rates of the two communication nodes, respectively. In Ref. [19], optimal beamforming design of AF MIMO one and two-way relay was studied, where a general iterative method to solve the problem was proposed, and the convexity of beamforming design problem was proved when the antenna number of two communication nodes go to infinity. So, only simple but complex iterative algorithms were proposed [17-19], and no further simplification methods were researched.
In this work, the result in Ref. [17] was extended to jointly design the relay beamfoming with transmitting and receiving beamforming at two source nodes. Besides giving an iterative method, two useful conclusions were carried out by analyzing the impact and structure perspective of the beamforming vectors (matrices). Based on these conclusions, a more general and simple method to accomplish the design without losing much system performance was proposed.
2 System model
A two-way MIMO relay channel is shown in Fig. 1. Sources S1 and S2 communicate with each other with the help of one relay node R equipped with M antennas. Each source node is assumed to be equipped with N antennas. Full cooperation among all relay antennas is also assumed.
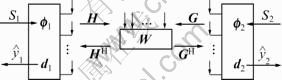
Fig. 1 System model of MIMO AF two-way relay channel
The system was operated in a TDD mode. Channel state changes slowly so that the estimated CSI keeps constant over multiple time slots. Assume that S1, S2 and R all know the CSI perfectly through some channel estimation techniques before transmitting.
The AF two-way protocol employed two time slots to complete the communication. In the first time slot, before transmitting, S1 and S2 processed their signals s1 and s2 to f1s1 and f1s2 using the transmit beamforming, under local power constraint P1 and P2, respectively,
x1=f1s1 (1)
x2=f2s2 (2)
where f1 and f2 are N×1 transmit beamforming vectors at S1 and S2, respectively. Sources S1 and S2 then transmitted the processed signal to relay R simultaneously. The received signal at R can be expressed as
r=Hx1+Gx2+v
where H and G are the channel matrices of S1→R and S2→R, and v is the complex Gaussian noise vector at R with ![]() The received signal at R was processed by the relay beamforming matrix W, and the transmitted signal from R is
The received signal at R was processed by the relay beamforming matrix W, and the transmitted signal from R is
xr=Wr
where xr is the M×1 transmitted signal vector of R with the transmit power constraint tr[E(xxH)]=Pr; W is the M×M relay beamforming matrix. In the second time slot, relay R broadcasts xr to S1 and S2. The received signals at S1 and S2 are represented as
![]()
![]()
where HHWGf1s1 and GHWGf2s2 are the SIs at S1 and S2, respectively. Variables n1 and n2 are the N×1 noise vectors at S1 and S2 with ![]() and
and ![]() Since both S1 and S2 know the signal they transmitted in the first time slot, self-interferences can be removed correspondingly. The remained signals at S1 and S2 are multiplied by 1×N receiver beamforming vectors d1 and d2, respectively,
Since both S1 and S2 know the signal they transmitted in the first time slot, self-interferences can be removed correspondingly. The remained signals at S1 and S2 are multiplied by 1×N receiver beamforming vectors d1 and d2, respectively,
![]()
![]()
Our main task is to jointly design the optimal transmitter beamforming vectors f1, f2, the receiver beamforming vectors d1, d2 and the relay beamforming matrix W.
3 Optimal MSMSE beamforming design
In this section, optimal beamforming at all nodes based on the MSMSE criterion are jointly designed. The sum of mean squared errors (SMSE) is defined as
c(f1, f2, d1, d2, W)=tr(R1)+tr(R2) (9)
where R1 and R2 are the error covariance matrices at S1 and S2, respectively,
![]() (10)
(10)
![]() (11)
(11)
So, the problem can be formulated as follows,
 (12)
(12)
Lagrange duality and the Karush-Kuhn-Tucker (KKT) conditions are adopted to solve this optimization problem. First, the Lagrangian is formed as
![]()
![]()
![]() (13)
(13)
By using the matrix derivation rules in Ref. [20], the following KKT conditions should be satisfied by the optimal solutions of this problem,
![]()
![]() (14)
(14)
![]()
![]() (15)
(15)
![]()
![]() (16)
(16)
![]()
![]() (17)
(17)
![]()
![]() (18)
(18)
where A=(Gf2)(Gf2)H, ![]() C=(Hf1)· (Hf1)H,
C=(Hf1)· (Hf1)H, ![]() and V=Gf2d1HH+Hf1d2GH. The optimal solutions of f1, f2, d1, d2 and W, which result in minimum SMSE, can be obtained as follows.
and V=Gf2d1HH+Hf1d2GH. The optimal solutions of f1, f2, d1, d2 and W, which result in minimum SMSE, can be obtained as follows.
1) Given all other beamformimg vectors, receiver beamforming d1 at S1 and d2 at S2 can be directly derived by Eqs. (16) and (17), respectively.
2) W can be expressed as a function of φ, W=f(φ) which is shown in Eq. (19) with all other beamformimg vectors given, where w=Vvec(WH), v=Vvec(V, M2, 1) and ![]() denotes the Kronecker product of matrices X and Y. Then, substituting Eq. (19) into
denotes the Kronecker product of matrices X and Y. Then, substituting Eq. (19) into ![]() 0, and numerically solving for the best φ which minimizes the SMSE for each time of iteration, W is solved.
0, and numerically solving for the best φ which minimizes the SMSE for each time of iteration, W is solved.
![]()
![]() (19)
(19)
2) According to Eq. (15), with the given d1, d2, φ and W, f1 can be expressed as a function of μ, which is shown as
![]()
![]() (20)
(20)
Then, substitute f1 into ![]() to solve for the best μ, and get the solution of f1. f2 can be solved in the same way.
to solve for the best μ, and get the solution of f1. f2 can be solved in the same way.
The solutions above are related to each other, so an iterative algorithm was proposed to solved, as given in Algorithm 1. Since each step in Algorithm 1 monotonically decreases SMSE, and the SMSE has a lower bound of zero, Algorithm 1 will conver after a finite number of iterations.
Algorithm 1:
Step 1 Set the initialization of f1, f2, d1, d2 and W as f1,0, f2,0, d1,0, d2,0 and W0, respectively. Set the maximum iteration number nmax, the counter k=1, the threshold ε to stop the iteration.
Step 2 Calculate d1,k, d2,k for the fixed f2, k-1, Wk-1 and f1, k-1Wk-l, respectively.
Step 3 Calculate φk, Wk for the fixed d1, k, d2, k, f1, k-1 and f2, k-1.
Step 4 Calculate μk and f1, k for the fixed d2, k, φk and Wk.
Step 5 Calculate γk and f2, k for the fixed d1, k, φk and Wk.
Step 6 If
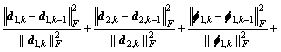
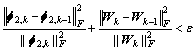
or k>nmax stop iteration, otherwise, K=K+1, return to Step 2.
4 Analysis and simplification
Lemma 1: The effect of beamforming pairs d1, f1 and d2, f2 which are designed to minimize the sum of mean square errors (SMSE) are equal to maximize the SNR at both nodes.
Proof: The effect of transmitting and receiving beamforming pair f2 and d2 will be proved here. The effect of the other beamforming pair f1 and d2 can be proved in the same way. The SMSE can be expressed as
![]()
![]()
![]() (21)
(21)
If W is set, in order to solve d1, d2, f1 and f2, Eq. (21) can be separated into two parts,
![]() (22)
(22)
![]()
Based on the received signal at S1 in Eq. , the received SNR at S1 is
![]()
In Eq. (16), it is denoted that HHWGf2=u and ![]()
![]() ,
,
![]() (25)
(25)
and Eq. (24) can be rewritten as
![]() (26)
(26)
By using Eq. (25), Eq. (22) can be rewritten as
![]() (27)
(27)
It can be known from Eq. (27), the minimum ![]() is equal to maximum
is equal to maximum ![]() the proof is completed.
the proof is completed.
Theorem 1: Rank of the optimal relay beamforming matrix Wopt, which attains the minimum MSMSE, is no larger than two. That is Rank(Wopt)≤2.
Proof: Let ![]()
![]() the signal value decomposition (SVD) of
the signal value decomposition (SVD) of ![]() and
and ![]() are denoted by
are denoted by![]() and
and ![]() respectively, where
respectively, where ![]() and
and ![]() are M×M matrices,
are M×M matrices, ![]() and
and ![]() are 2×2 diagonal matrices,
are 2×2 diagonal matrices, ![]() and
and ![]() are 2×2 matrices. Matrices
are 2×2 matrices. Matrices![]() and
and![]() can be expressed as
can be expressed as ![]() and
and ![]() respectively, where
respectively, where ![]() and
and ![]() are M×2 unitary matrices,
are M×2 unitary matrices, ![]() and
and ![]() are M×(M-2) unitary matrices whose columns are orthogonal with the columns of
are M×(M-2) unitary matrices whose columns are orthogonal with the columns of ![]() and
and ![]() , respectively. So, the relay beamfoming matrix W can be expressed as
, respectively. So, the relay beamfoming matrix W can be expressed as
![]()
![]() (28)
(28)
where Ψ1, Ψ2, Ψ3 and Ψ4 are 2×2, 2×(M-2), (M-2)×2 and (M-2)×(M-2) are complex matrices, respectively. Substitute Eq. (28) into Eq. (18), we obtain
![]()
![]()
![]() (29)
(29)
Multiply the left side and the right side of Eq. (29) with ![]() and
and ![]() respectively. Then,
respectively. Then,
![]()
![]()
![]() (30)
(30)
From Eq. (30), among Ψ1, Ψ2, Ψ3 and Ψ4, optimal solution of W is only related to Ψ1, and in order to efficiently utilize the relay power Pr, Ψ2, Ψ3 and Ψ4 should be equal to 0. So, the optimal relay beamforming matrix should have the following structure,
![]() (31)
(31)
Rank(Wopt)=Rank(Ψ1)≤2, the proof is completed.
Based on the above conclusions, Algorithm 1 can be simplified to make the algorithm more applicable and faster in implementing without losing much performance. To calculate f2, Eq. (26) can be further written as
![]() (32)
(32)
where ![]() As we know, to maximize
As we know, to maximize ![]() let
let ![]() where
where ![]() is the singular vector corresponding to the largest singular value of
is the singular vector corresponding to the largest singular value of ![]() while
while ![]() In order to get Wopt, Eq. (31) can be further written as
In order to get Wopt, Eq. (31) can be further written as
![]() (33)
(33)
All the beamforming vectors (matrices) can be obtained by the following steps.
1) Given all other beamforimg vectors, receiver beamforming d1 and d2 can be directly derived by Eqs. (16) and (17), respectively.
2) Transmit beamforming f1, f2 can be solved as mentioned in Eq. (32).
3) With all other beamfoming vectors given, the partial derivatives can be resolved with respect to a, b, c, d and ξW, and set to be zero, respectively. And W is solved.
This method is much simpler to implement because of avoiding searching for μ, γ. And f1, f2 can be gotten via a one-step SVD decomposition. No matter how many antennas the relay node is equipped with, we can recast W to a 2×2 matrix.
5 Simulation results
In our simulation, H and G are generated by independent and identically distributed complex Gaussian distribution with zero mean and unit variance. All simulations are carried out for binary phase shift keying (BPSK) modulation with ![]() and P1=P2= (1/M)Pr.
and P1=P2= (1/M)Pr.
Obviously, computational complexity of the optimal method and the simple one are dominated by Eqs. (19) and (32), respectively, whose complexity are O((M2)3)= O(M6) and O(N3). Figure 2 shows the average iteration times when the two methods are implemented, which are both simulated at SNR=15 dB but with different antenna numbers M=N=2 and M=N=3. It can be seen that the iteration times of simplified method is always one time larger than the optimal one at M=N=2 and M=N=3. So, considering the computational complexity, the simplified method is much more suitable to apply.
Figure 3 shows the performance of the average BER of S1 and S2 of different algorithms proposed, compared with the scheme in Ref. [17], which is modified to transmit one data stream as well as our schemes. A simplified method which only has the transmitting and receiving beamforming at S1 and S2, where the relay beamforming is simplified to W=ρIM with ρ= ![]() is also proposed for comparison. It can be noted that, the BER performance of the optimal iterative algorithm with the transmit beamforming f1 and f2 is improved by 5 dB at BER= 10-3 when M=N=2. It is shown that when the relay power is equally allocated across the M antennas, with the transmitting and receiving beamforming, the BER performance at RBE=10-3 is still about 1dB better than the scheme in Ref. [17] when M=N=2, and the algorithm is much simpler now. It also demonstrates that, with the simple MSMSE algorithm, the BER performance is about 1.5 dB less than the optimal one at RBE=10-3 when M=N=2, but the latter simplified algorithm is much more applicable. It can be further noted that, when the antenna number, M and N are increased, the BER performance of each method is greatly improved due to the increased diversity. The performance of the simplified method is about 1 dB worse than the optimal one when M=N=2, but the performance gap between them is negligible when M=N=3.
is also proposed for comparison. It can be noted that, the BER performance of the optimal iterative algorithm with the transmit beamforming f1 and f2 is improved by 5 dB at BER= 10-3 when M=N=2. It is shown that when the relay power is equally allocated across the M antennas, with the transmitting and receiving beamforming, the BER performance at RBE=10-3 is still about 1dB better than the scheme in Ref. [17] when M=N=2, and the algorithm is much simpler now. It also demonstrates that, with the simple MSMSE algorithm, the BER performance is about 1.5 dB less than the optimal one at RBE=10-3 when M=N=2, but the latter simplified algorithm is much more applicable. It can be further noted that, when the antenna number, M and N are increased, the BER performance of each method is greatly improved due to the increased diversity. The performance of the simplified method is about 1 dB worse than the optimal one when M=N=2, but the performance gap between them is negligible when M=N=3.
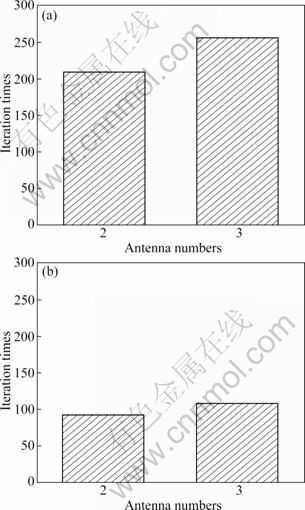
Fig. 2 Average iteration times of two methods at M=N=2 (a) and M=N=3 (b) with SNR=15 dB, threshold ε=10-5
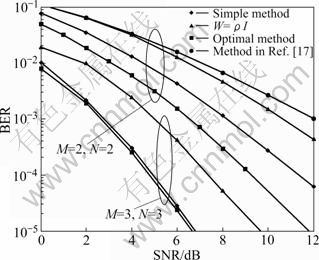
Fig. 3 BER comparison of schemes of M=N=2 and M=N=3
6 Conclusions
1) A general iterative algorithm to design the optimal cooperative beamforming of AF two-way relay channels based on MSMSE criterion is proposed in this work. After investigating the optimal method, it is proved that the effect of two transmitting and receiving beamforming pairs at two source nodes is maximizing the receive SNR. When there is one data stream being transmitted from both source nodes, the rank of optimal relay beamforming matrix is no larger than 2.
2) With both transmitting and receiving beamformings, the BER performance of optimal algorithm is much better than the same scheme without transmitting beamforming at two source nodes under the same power constraint and noise distribution assumption. The performance gap between the optimal algorithm and the simplified algorithm is getting smaller when the antenna number of all nodes is increased. When M≥3, the simplified method can be used to substitute the optimal one, because it can be calculated much faster and easier.
References
[1] LANEMAN J N, TSE D N C, WORNELL G W. Cooperative diversity in wireless networks: Efficient protocols and outage behavior [J]. IEEE Transaction Information Theory, 2004, 50(12): 3062-3080.
[2] BOLCSKEI H. Capacity scaling laws in MIMO relay networks [J]. IEEE Trans Wireless Commun, 2006, 5(6): 1433-1444.
[3] WYREMBELSKI R, OECHTERING T, BJELAKOVIC I. Capacity of Gaussian MIMO bidirectional broadcast channels [C]// IEEE International Symposium on Information Theory. 2008: 584-588.
[4] VAZE R, HEATH R. Optimal amplify and forward strategy for two-way relay channel with multiple relays [C]// IEEE Information Theory Workshop on Networking and Information Theory. 2009: 181-185.
[5] SHI H, ABE T, ASAI T, YOSHINO H. Relaying schemes using matrix triangularization for MIMO wireless networks [J]. IEEE Trans Commun, 2007, 25(2): 1683-1688.
[6] YI Z, KIM I M. Joint optimization of relay-precoders and decoders with partial channel side information in cooperative networks [J]. IEEE J Select Areas Commun, 2007, 25(2): 379-389.
[7] KRAMER G, GASTPAR M, GUPTA P. Cooperative strategies and capacity theorems for relay networks [J]. IEEE Transaction Information Theory, 2005, 51(9): 23037-3063.
[8] LIANG Ying-chang, ZHANG Rui. Optimal analogue relaying with multi-antennas for physical layer network coding [C]// IEEE International Conference on Communication, 2008: 3893-3897.
[9] ZHENG L, TSE D N C. Diversity and multiplexing: A fundamental tradeoff in multiple-antenna channels [J]. IEEE Transaction Information Theory, 2003, 49(5): 1073-1096.
[10] WANG B, ZHANG J, HOST-MADSEN A. On the capacity of MIMO relay channels [J]. IEEE Transaction Information Theory, 2005, 51(1): 29-43.
[11] JING Yin-di, JAFARKHANI H. Network beamforming using relays with perfect channel information [J]. IEEE Transaction Information Theory, 2009, 55(6): 2499-2517.
[12] JING Yin-di, JAFARKHANI H. Network beamforming using relays with perfect channel information [C]// IEEE International Conference on Acoustics, Speech and Signal Processing, 2007: 473-476.
[13] KIM S, CHUN J. Network coding with linear MIMO pre-equalizer using modulo in two-way channel [C]// IEEE Wireless Communications and Networking Conference. 2008: 517-521.
[14] ZHANG Rui, LIANG Y, CHAI C C, CUI S. Optimal beaforming for two-way multi-antenna relay channel with analogue network coding [J]. IEEE J Select Areas Commun, 2009, 27(5): 699-712.
[15] JOUNG J, SAYED A H. Multiuser two-way amplify-and-forward relay processing and power control methods for beamforming systems [J]. IEEE Transaction Signal Process, 2010, 58(3): 1833- 1846.
[16] SAMPATH H, STOICA P, PAULRAJ A. Generalized linear precoder and decoder design for MIMO channels using the weighted MMSE criterion [J]. IEEE Transaction Commun, 2001, 49(12): 2198-2206.
[17] LEE N, PARK H, CHUN J. Linear precoder and decoder design for two-way of MIMO relaying system [C]// IEEE Vehicular Technology Conference. 2008: 1221-1225.
[18] LEE K, LEE K W, SUNG H, LEE I. Sum-rate maximization for two-way MIMO amplify-and-forward relaying systems [C]// IEEE Vehicular Technology Conference. 2009: 26-29.
[19] LEE K, SUNG H, PARK E, LEE I. Joint Optimization for one and two-way MIMO AF multiple-relay systems [J]. IEEE Transaction Wireless Commun, 2010, 9(12): 3671-3681.
[20] LUTKEPOHL H. Handbook of matrices [M]. New York: Wiley, 1996.
(Edited by DENG Lü-xiang)
Foundation item: Project(60902092) supported by the National Natural Science Foundation of China
Received date: 2011-07-22; Accepted date: 2011-11-19
Corresponding author: ZHENG Lin-hua, PhD; Professor; Tel: +86-731-84576407; E-mail: lhzheng131@sohu.com
Abstract: An optimal cooperative beamforming for the amplify-and-forward (AF) MIMO two-way relay channels was designed. Supposing the channel state information (CSI) was perfectly known by the receiver and transmitter as well as the relay, optimal beamforming vectors (matrices) of all nodes were jointly designed based on the criterion of minimizing the sum mean square errors (MSMSE). The analysis result shows that the performance effect of transmitting and receiving beamforming pairs is to maximize the receive signal-to-noise ratio (SNR) at two communication nodes, and the rank of the optimal relay beamforming matrix is no larger than two when there is only one data stream at each source node. A simplified algorithm was put forward to accomplish the design based on the analysis conclusions. Simulation results provide that the system performance, which is characterized in terms of bit error rates (BER), is significantly improved by cooperative beamforming, and the performance of the simplified method is not only very close to the optimal one but also with faster iteration speed and much lower computational complexity.
- MSMSE-based optimal beamforming design and simplification on AF MIMO two-way relay channels


