Article ID: 1003-6326(2005)02-0419-04
Critical misfit of epitaxial growth metallic thin films
LI Jian-Chen(李建忱), LIU Wei(刘 伟), JIANG Qing(蒋 青)
(Key Laboratory of Automobile Materials, Ministry of Education;
Department of Materials Science and Engineering, Jilin University, Changchun 130025, China)
Abstract:
The critical misfit of epitaxial growth metallic thin films fc was thermodynamically considered. It is found that there exists a competition between the energy of the misfit dislocation of film and non-coherent interface energy of film-substrate. Equilibrium between these energies was present at a critical atomic misfit fc. When the atomic misfit is larger than the critical value, epitaxial growth does not occur. The critical misfit of the epitaxial growth thin films can be predicted. The results show that fc is proportional to the non-coherent interface energy of the film-substrate, and inversely proportional to the elastic modulus and the thickness of the film.
Key words:
epitaxial growth film; atomic misfit; dislocation; interface energy CLC number: O484.1;
Document code: A
1 INTRODUCTION
Thin metallic films epitaxially grown on metallic substrates have been the subjects of many studies because they present very unusual chemical, electronic and magnetic properties, which differ from the corresponding bulk counterparts[1, 2]. However, the film and the substrate generally have different lattice parameters. As a result, the lattice mismatch exists at the film/substrate interface and internal stresses are induced in the system. The epitaxial growth model is affected by the corresponding strain energy induced by the atomic misfit of film-substrate. When an epitaxial growth thin film is deposited onto a substrate that has a different lattice parameter than that of the film, the lattice misfit can be accommodated in two ways: the film can be elastically strained in order to bring it into registry with the substrate and/or the misfit can be accommodated by misfit dislocations within the film-substrate interface.
The concept of a limiting misfit as the upper limit of misfit below which epitaxial growth may occur was introduced by Royer, which motivated Franck and Merwe[3] to introduce the relevant concepts of misfit strain, misfit dislocations, critical misfit and critical thickness. The critical misfit fc is homogeneously strained into registry with the substrate, and the critical thickness is the critical layer thickness above which an interface of given natural misfit loses registry by the introduction of misfit dislocations. The critical misfit and the thickness of the epitaxial growth films before misfit dislocations appear were predicted by many researchers[4-7]. However, misfit dislocations occur practically in most epitaxial growth films. With strain increasing, the energy of the film increases, the strain in the film is relaxed by formation of the misfit dislocations. When the strain in the film is relaxed entirely by the misfit dislocations, the interface energy of the film-substrate is mainly the misfit dislocation energy. Once it reaches some value that it is larger than the non-coherent interface energy of film-substrate, the interface is completely non-coherent. Therefore, there must be the critical atomic misfit of the film-substrate fc for epitaxial growth. When the misfit is larger than critical value fc, epitaxial growth film cannot be obtained. In this contribution, fc is calculated based on thermodynamics and dislocation theory.
2 MODEL
When the strain in the film is relaxed entirely by the formation of the dislocations, the strain energy disappears, its interface free energy is the energy of misfit dislocations. When the energy of film reaches the non-coherent interface energy, the interface becomes completely non-coherent. For an epitaxial growth film, the interface of the film and the substrate must be coherent or semi-coherent.
When the solid is isotropic, the atomic misfit of film f=|hf-hs|, where hf and hs are the atomic distances of the nearest neighbor of the film and substrate respectively.
The non-coherent interface energy of the film Uin can be simply calculated by
Uin=γssAf(1)
where γss is the solid-solid interface energy, Af is the area of the interface.
It is well known that a liquid may be regarded as a solid with such a high concentration of dislocation cores that these are in contact everywhere[8]. Based on this theory, γss is considered to be twice of the solid-liquid interface energy γsl approximately[9], namely
γss≈2γsl(2)
Over 50 years ago, Turnbull and Cech[10, 11] observed that the interfacial free energies of a variety of metallic elements exhibited a linear correlation with the enthalpy of fusion, and proposed a famous empirical relationship as follows:
γsl=khHm/Vm(3)
where k is a constant, h denotes the atomic diameter, Hm is the melting enthalpy of crystals, Vm denotes the molar volume. The coefficient of k is considered to be between 0.32 and 0.45. This relationship provides an important empirical “rule-of-thumb” for estimating interfacial free energies, but lacks a compelling physical explanation[12].
γsl has been deduced by use of Gibbs-Thomson equation and our model for the size-dependent melting temperature as follows[13-15]:
γsl=2hSvibHm/(3VmR)(4)
[BJ(,,,][BJ)] Vol.15 №.2 Critical misfit of epitaxial growth metallic thin films where R is the ideal gas constant, Svib is the vibrational part of the overall melting entropy Sm. For metallic crystals, Svib≈Sm=Hm/Tm, and Tm is the bulk melting temperature[16]. The predicted γsl for different types of crystals, such as “true metals” Au, “meta metals” Pb, semiconductors Bi, ionic crystals ice and organic crystals benzene and naphthalene, are confirmed by available experimental results in the experimental error range[13]. It is obvious that when k=2Sm/3R, Eqn.(3) equals to Eqn.(4), which suggests that both Hm and Sm affect the size of γsl. Thus, Turnbulls empirical equation is improved in our model.
Substituting Eqn.(4) into Eqn.(2) yields
γss=4hSvibHm/(3VmR)(5)
The solid-solid interface consists of different crystals, as a first order approximation, a mean value for γsl is taken:
![]()
where ![]()
![]() ,
,![]() , and
, and ![]() are the mean values of corresponding amounts of the two halves. It can be found that this approximation is proper for bicrystals from Table 1 and Fig.1.
are the mean values of corresponding amounts of the two halves. It can be found that this approximation is proper for bicrystals from Table 1 and Fig.1.
The comparisons of the model predictions for γss in terms of Eqn.(6) with other theoretical results γ′ss calculated in terms of the embedded atom method(EAM) interaction potentials are shown in Table 1 and Fig.1. Fig.1 as well as Table 1 reveal a good quantitative agreement between our theory and other theoretical values for the interface energy. The free energy of the solid-solid interface depends on not only the melting enthalpy, but also the vibrational component of the overall melting entropy.
Table 1 Comparison of γss by model prediction in terms of Eqn.(6) with other theoretical γ′ss

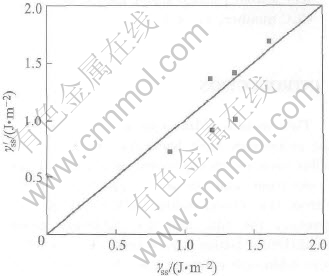
Fig.1 Graph comparison of γss by model prediction in terms of Eqn.(6) with other theoretical γ′ss
The interface free energy of the fully relaxed film can be expressed as the sum of the misfit dislocation energy Ud induced by dislocation energy being equal to the product of misfit dislocation energy of a single dislocation(ud) and the dislocation number(N) on the area of the interface of the film-substrate Af. We have introduced the simplifying assumption that the film and substrate are elastically equivalent. It is assumed that dislocation is edge one that is parallel to x-axis or y-axis:
![]()
where Ef and νf denote the elastic modulus and the Poissons ratio of the film, l is the length of a dislocation. δ is an effective dislocation stress field radius, which is often approximated as the smaller of the film thickness t[16]. b is the Burgers vector, which is equal to the average atomic distance of the nearest neighbor of the film and substrate. N=Af /(lD) with D=b/f being the distance between two neighbor dislocations along x-axis or y-axis. Thus, the total number along two axes N=2Ni=2fAf/(l). Let Ud=Nud, then
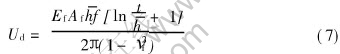
Let Ud=Uin in terms of Eqns.(1) and (7) with a corresponding critical atomic misfit fc where the interface transforms from a semi-coherent interface to a non-coherent interface due to the requirement of minimum of the interface energy. ![]() , or
, or
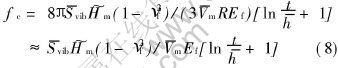
3 RESULTS AND DISCUSSION
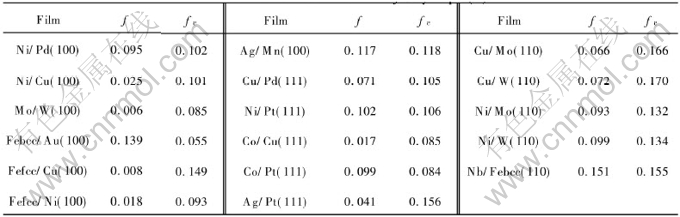
The above result implies that the film cannot grow epitaxially when f is larger than fc. In light of Eqn.(8), fc may shift to a larger value through increasing Hm value of substrate according to the definition of [AKH-]m. The calculative results of maximal fc by Eqn.(8) for some epitaxial growth thin films on different substrates are listed in Table 3, where the necessary parameters of Eqn.(8) are shown in Table 2, here the minimum value of the film thickness t is one atomic layer, i.e. t/[AKh-]≈1. The critical misfits in Table 3 show that other epitaxial growth films can be obtained, except Febcc/Au(100) and Co/Pt(111) films. The results are approved by previous experiments. The above results show that the epitaxial growth film exactly depends on the energetic conditions. Moreover, as mentioned above, a substrate with larger Hm value, and small thickness and elastic modulus of film will benefit obtaining an thin film by epitaxial growth.
Table 2 Needed parameters for calculation of Eqn.(8)
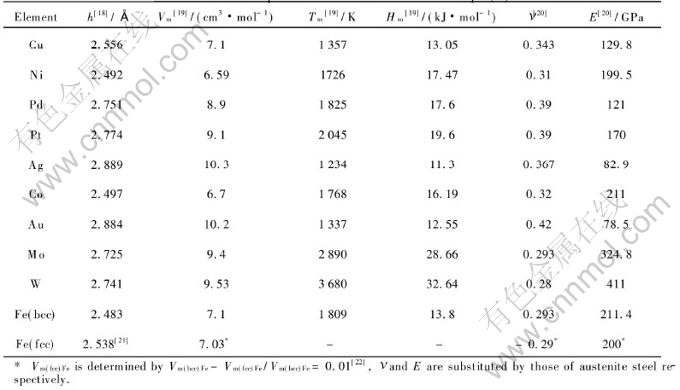
Table 3 Calculative results of fc by Eqn.(8)
4 CONCLUSIONS
In summary, through a thermodynamic considering, the critical atomic misfit of epitaxial growth thin film is determined by Eqn.(8). It is found that fc is related with not only Hm value of the materials, but also the elastic modulus and the thickness of the film. fc is proportional to the non-coherent interface energy of the film-substrate, and inversely proportional to the elastic modulus and the thickness of the film.
REFERENCES
[1]Dreyssé H, Demangeat C. Theoretical approaches of magnetism of transition-metal thin films and nanostructures on semi-infinite substrate [J]. Surface Science Report, 1997, 28(3-4): 65-122.
[2]Pearton S J, Abernathy C R, Norton D P, et al. Advances in wide bandgap materials for semiconductor spintronics [J]. Materials Science Engineering R, 2003, 40(4): 137-168.
[3]van der Merwe J H. Interfacial energy: bicrystals of semi-infinite crystals [J]. Progress of Surface Science, 2001, 67(1-8): 365-381.
[4]van der Merwe J H. Crystal interfaces(part Ⅱ)—finite overgrowths [J]. Journal of Applied Physics, 1963, 34(1): 123-127.
[5]Jesser W A, van der Merwe J H. An exactly solvable model for calculating critical misfit and thickness in epitaxial superlattices: layers of equal elastic constants and thicknesses [J]. Journal of Applied Physics, 1988, 63(5): 1509-1517.
[6]Cammarata R C, Sieradzki K, Spaepen F. Simple model for interface stresses with application to misfit dislocation generation in epitaxial thin films [J]. Journal of Applied Physics, 2000, 87(3): 1227-1234.
[7]Matthews J W. Epitaxial Growth [M]. New York: Academic, 1975. 559.
[8]Kuhlmann-Wilsdorf D. Theory of melting [J]. Physical Review A, 1965, 140(5): 1599-1610.
[9]Kotzé I A, Kuhlmann-Wilsdorf D. A theory of the interfacial energy between a crystal and the melt [J]. Applied Physics Letters, 1966, 9(2): 96-99.
[10]Turnbull D. Formation of crystal nuclei in liquid metals [J]. Journal of Applied Physics, 1950, 21(10): 1022-1028.
[11]Turnbull D, Cech R E. Microscopic observation of the solidification of small metal droplets [J]. Journal of Applied Physics, 1950, 21(8): 804-810.
[12]Laird B B. The solid-liquid interfacial free energy of close-packed metals: hard-spheres and the Turnbull coefficient [J]. Journal of Chemical Physics, 2001, 115(7): 2887-2888.
[13]Jiang Q, Shi H X, Zhao M. Free energy of crystal-liquid interface [J]. Acta Mater, 1999, 47(7): 2109-2112.
[14]Jiang Q, Shi H X, Zhao M. Melting thermodynamics of organic nanocrystals [J]. Journal of Chemical Physics, 1999, 111(5): 2176-2180.
[15]Wen Z, Zhao M, Jiang Q. Size range of solid-liquid interface energy of organic crystals [J]. Journal of Physical Chemistry B, 2002, 106(16): 4266-4268.
[16]Hirth J P, Lothe J. Theory of Dislocations [M]. New York: John Wiley Sons, 1982. 59-96.
[17]van der Merwe J H. Interfacial energy: bicrystals of semi-infinite crystals [J]. Progress of Surface Science, 2001, 67(1-8): 365-381.
[18]King H W. Physical Metallurgy [M]. Amsterdam: North-Holland Physics Publishing House, 1983. 63-65.
[19]Sargent-Welch Scientific Company. Periodic Table of the Elements [M]. Illinois: Skokie, 1979. 1.
[20]Brandes E A. Smithells Metals Reference Book(6th edition) [M]. London: Butterworth & Co Ltd, 1983. 15.
[21]Luches P, Gazzadi G C, di Bona A, et al. Epitaxial growth of ultrathin Fe films on Ni(001): a structural study [J]. Surface Science, 1999, 419(2-3): 207-215.
[22]American Society for Metals. Fan Y D, Trans. Metals Handbook (Vol. 2, 9th edition) [M]. Beijing: China Machine Press, 1979. 906-1057.
Foundation item: Project(2004CB619301) supported by the National Key Fundamental Research and Development Program of China; Project(50025101) supported by the National Natural Science Foundation of China
Received date: 2004-11-23; Accepted date: 2005-01-18
Correspondence: JIANG Qing, Professor, PhD; Tel: +86-431-5095371; E-mail: jiangq@jlu.edu.cn
[7]Matthews J W. Epitaxial Growth [M]. New York: Academic, 1975. 559.
[8]Kuhlmann-Wilsdorf D. Theory of melting [J]. Physical Review A, 1965, 140(5): 1599-1610.
[16]Hirth J P, Lothe J. Theory of Dislocations [M]. New York: John Wiley Sons, 1982. 59-96.
[19]Sargent-Welch Scientific Company. Periodic Table of the Elements [M]. Illinois: Skokie, 1979. 1.


