具有反馈数据丢包的网络化控制电力无功优化改进算法

彭可，盘清琳，邵添，聂健，李国平，李仲阳，金耀

(湖南师范大学 工程与设计学院，湖南 长沙，410081)

摘 要：

道中通信时延、远动数据丢失对于电力无功优化的影响。针对由于时延与丢包等因素导致系统状态反馈变量出现误差和缺失的情况，提出一种具有反馈数据缓存的网络化控制无功优化改进算法。该算法在状态估计算法的基础上，引入接收缓存器对反馈通道中状态变量的缺失或误差进行修正，以保证无功优化运行时所需要的远程观测数据。采用差分进化算法，对于IEEE 14节点及IEEE 30节点系统进行仿真研究。研究结果表明：当网络化控制无功优化系统中反馈通道的量测数据出现缺失或误差时，利用改进后的状态估计方法可以较好地求出系统的状态量，并能应用于后续的相应无功优化计算过程，从而保证系统性能达到较优状态。

关键词：

网络化控制；无功优化；状态估计；反馈数据丢包；接收缓存；差分进化算法；

中图分类号：TM714.3；TM761.1          文献标志码：A         文章编号：1672-7207(2013)09-3752-07

Improved algorithm for network-controlled reactive power optimization with data packet dropout on feedback channel

PENG Ke, PAN Qinglin, SHAO Tian, NIE Jian, LI Guoping, LI Zhongyang, JIN Yao

(College of Engineering and Design, Hunan Normal University, Changsha 410081, China)

Abstract: The impacts of network communication delay and data packet dropout on reactive power optimization (RPO) were analyzed. In view of the feedback state variables’ error and absence caused by the network delay and data loss on the feedback channels, an improved network-controlled RPO algorithm based on receiving buffer to the feedback data packet dropout was proposed. It introduced the state estimation (SE) algorithm combined with the receiving buffer, to correct the state variables’ error or absence on the feedback channel, which provided the necessary remote observation data needed in the following RPO calculation. Taking the differential evolutionary (DE) algorithm as an example, the simulations were researched and analyzed on the IEEE 14 and IEEE 30 bus system. The results show that when there is absence or error of observation data on the feedback channel of the network-controlled RPO system, the improved SE algorithm can well be used to estimate the state variables and accordingly be applied in the subsequent RPO calculations. Therefore, the system performance is ensured to achieve an optimal state.

Key words: network control; reactive power optimization; state estimation; feedback data packet dropout; receiving buffer; differential evolutionary algorithm

电网实时产生大量数据，电力系统的无功优化(reactive power optimization, RPO)就是通过分析处理这些数据，对于相关参数进行调控，使系统电压稳定、网损减小，从而安全高效运行。随着国内调度自动化水平的提高，需要实时对电力系统的运行状态进行监控。网络化控制无功优化系统(network-controlled RPO)是将网络化控制(network control system, NCS)技术引入电力无功优化所形成的实时控制系统，该系统有效解决了日益增长的电力系统实时性和优化性调控问 题^[1-2]。数据时延和丢包一直以来都是网络化控制领域的重要研究问题之一。在网络化控制无功优化系统中，时延和丢包会导致系统无法接收到完整的数据，从而使得无功优化性能下降，影响电力系统的优化运行。在网络化控制无功优化系统中，时延或丢包可能出现在传输网络的前向通道和反馈回路中。针对前向通道数据丢包的处理，前期已经取得了一定的进展。文献[1]提出采用去冗-保持处理方法解决前向通道出现数据丢包的问题，实验结果验证了该算法的可行性；文献[2]针对仅能处理前向通道数据丢包的缺陷，将去冗-保持处理方法进行了扩展，可以处理较少数目的反馈通道数据丢包，同时对无功优化引进多目标进化算法，并对算法本身进行了改进，实验结果也验证了所提出算法的优越性。但是，上述研究均未能完全解决反馈回路中数据时延与丢包的问题。状态估计是当代电力能量管理系统(EMS)的重要组成部分^[3-4]。它通过分析处理电网的实时量测数据，获得系统的状态和运行方式，是后续最优潮流计算和调度的基础^[5]。无功优化控制是电力系统调度中心的重要组成部分，将状态估计方法引入无功优化中具有可行性。针对前述的网络化控制无功优化系统中反馈通道数据丢包问题，本文作者提出将状态估计法应用于网络化控制无功优化系统，并在估计器中设置接收缓冲区，利用已有的缓冲反馈量测值，估计系统的真实运行状态，从而有效地应对反馈回路的数据丢包问题；进一步结合IEEE14和IEEE30节点系统，采用差分进化算法为例进行仿真实验，验证该算法的可行性和有效性。

1  反馈通道中数据丢包问题的描述

1.1  网络化控制无功优化系统的反馈通道数据丢包问题

具有反馈数据丢包的网络化控制无功优化系统结构如图1所示。其控制数据的流程如下：(1) 状态采集器采集电力系统实时数据，通过反馈网络通道传输至无功调节控制器；(2) 无功调节控制器接收到状态采集器传来的反馈量测数据，进行优化算法运算，计算所得的输出控制量再通过前向网络通道，传输至无功执行器；(3) 无功执行器接收到优化输出控制量，执行电力系统相关参数的调节操作，使系统处于无功最优状态运行。从图1可以看出：各种数据在状态采集器、无功调节控制器和无功执行器等之间相互通过网络通讯进行传输。

图1  网络化控制无功优化系统具有反馈数据丢包的结构图

Fig.1  Control structure of network-controlled RPO system with feedback data packet dropout

通常可将状态采集器至无功调节控制器、无功调节控制器至无功执行器在网络中的传输状态分别看成2个开关S₁和S₂；未发生数据丢包可视为开关闭合，发生数据丢包则视为开关断开。假设无功调节控制器至无功执行器的通道时延很小且未发生丢包，即开关S₂处于连通状态；而状态采集器至无功调节控制器的传输时延大于采样周期(即为发生丢包)，开关S₁处于断开状态。此时，网络化控制无功优化系统可看作具有反馈回路数据丢包情况。

在图1中，采集的实时反馈数据x(k)包括电网中电压、电流和相位以及开关的闭合等状态变量；无功优化计算的结果为输出控制量，包括发电机输出电压、有载变压器档位、电容器补偿容量等控制变量；τ_sc为状态传感器至调节控制器之间反馈网络通道的传输时延；τ_ca为调节控制器到执行器之间前向网络通道的传输时延^[1]。

由于开关S₁断开(反馈回路发生了数据丢包)，系统不能实时接收并得到电网状态的完整反馈数据x(k)，因此，无功调节控制器进行优化计算时，只能基于系统的部分实时反馈状态x(k-τ_sc)，造成优化计算结果与完整状态反馈情况下的相比存在误差，从而导致系统原有的优化算法效果下降。

1.2  网络化控制无功优化系统的状态估计法

状态估计法的实质是一种实时潮流计算，也可称为滤波^[6-7]。它根据网络化量测系统的冗余度，实时预测电力系统的实际运行状态，为无功优化运算提供系统真实状态，进而分析和调度电网的运行趋势^[8-9]。

针对上述具有反馈数据丢包的网络化控制无功优化问题，将常规状态估计算法进行扩展：通过在估计器端放置有限缓存器，将缓存器中任意固定时刻的数据达到看作仅有临时丢包的NCS系统，并利用缓存数据来对网络传输的不确定性时延和丢包进行补偿，从而实现对于反馈变量的估计，以解决反馈数据丢包对后续无功优化算法的影响^[10]。这种处理在理论上具有合理性和必然性，其系统结构图如图2所示。

图2  具有接收数据缓冲的网络化控制无功优化系统结构图

Fig.2  Control structure of network-controlled RPO system with receiving buffer to feedback data packet dropout

2  具有反馈数据丢包的无功状态估计算法分析及实现

2.1  具有接收缓存的无功状态估计分析

网络化控制无用优化系统反馈通道的传输过程中存在有限的马尔科夫延迟和丢包情况，为了解决这类通信受限的状态估计问题，在控制器端设置了接收缓存器。

针对反馈通道出现的延迟和丢包，定义随机变量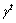用以描述t时刻缓存器中数据包的到达过程：

      (1)

其中：，即t≥k。假设系统所能接受的最大时延为M，即；若反馈数据包的时延超过，则可将该数据包视为丢包，测量值的时延的数学模型为

       (2)

其中：t_k表示量测值z(k)到达估计器的时间。

在状态估计器端的接收缓存中，假设数据包的延迟是以下概率函数的多状态马尔科夫链：

           (3)

其中：k≥0, 。进而得到该马尔科夫延迟的一步转移矩阵。

在任意时刻t，缓存器中所存储的数值为，。因为数据已经发生丢失，并且丢失情况已知，故不需考虑观测噪声在数据传输前后问题，可以表示为

              (4)

由此，可以将具有数据丢包的状态估计问题描述为：在具有最大延迟并且延迟满足马尔科夫转移矩阵统计特性情况下，根据状态估计器端接收缓存中所存储的数据对于系统状态x(t)进行估计，可以得到估计值，并使得估计误差满足某一性能指标，即

         (5)

其中：为系统初始状态量；为延时为0的马尔科夫延迟转移矩阵；表示t时刻估计器可能接收到的观测值；。

2.2  具有反馈数据丢包的无功状态估计算法实现

状态估计计算只有在系统可观的前提下才能进行，所以，必须先对系统的可观性进行判定。系统的可观性判定有2种方法：数值分析法和拓扑分析法。数值分析法就是通过判定系统量测数据的雅克比矩阵是否满秩来确定。采用数值分析法要进行浮点运算，计算量大，易受舍入误差影响，容易误判，所以，一般采用拓扑算法，通过树的搜索，判明其可观测性^[11-13]。本文中由于网络化控制无功优化系统的反馈传输通道发生了数据丢包，若导致系统的可观性必要量测数据缺失，造成系统不可观时，则需先将所有支路量测岛根据反馈量测量的输入情况最大可能地合并成1个可观测岛；对于无法合并的部分，适当地依照历史和经验值加入伪量测量，以实现整体系统可观测^[14-15]。

当网络化控制无功优化系统中状态反馈数据处于可观测的条件下，针对反馈通道中数据丢包导致的状态量误差，采用前述改进状态估计方法，利用已有获得的量测值，估计系统的真实状态，并对估计结果进行不良数据辨识与处理，从而降低由数据丢包导致的状态变量发生缺失或误差对无功优化计算的影响。加权最小二乘法是状态估计最常用的方法，本文采用文献[16]中的加权最小二乘法作为反馈状态的估计算法。在反馈回路出现数据丢包情况下，基于基尔霍夫定律建立状态估计的基本数学模型。具体如下。

          已知由状态采集器通过反馈通道传送至无功控制器且具有误差的不完整状态量x(节点的电压幅值和相角等)、网络参数p和结线状态s；针对反馈数据丢包在控制器端设置接收缓存。将上述反馈状态量均先存入接收缓存中，再由估计器从接收缓存中取出使用。建立无功状态估计的非线性量测方程如下：

          (6)

式中：z为m维量测向量，由于电网电压的相位角难于测量，而功率相对容易测量，因此，本文的量测量为节点及支路的有功功率和无功功率^[16]；为以电网参数为自变量的函数向量，通常将其简化为h(x)；b为不良数据分量；v_p为网络参数误差分量；v_z为零期望的测量数据误差分量，这里是根据网络状态设置且相互独立的m维分量，即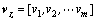是一个服从期望为0、方差为的正态分布^[5]。

求得量测值z后，建立状态估计的目标函数：

         (7)

其中：为权重值(它反应出量测精度)。当目标函数达到最小时，即可得到状态估计向量。

加权最小二乘(WLS)线性状态估计解式为

            (8)

其收敛判据为

≤                 (9)

式中：i表示向量x中的序号；为第n次迭代估计结果的误差；为迭代截止常数，一般为基准值的10^-6~10^-4倍。

当h(x)为x的非线性函数时，网络化控制无功优化系统中具有反馈数据丢包的状态估计算法实现步骤如下。

Step 1: 由无功调节控制器接收的初始状态量计算非线性函数和雅克比矩阵。

Step 2: 从缓存器中取出反馈量，重新求取量测量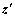和，计算残差和目标函数；并由雅克比矩阵计算信息矩阵和向量(其中，n表示迭代序号)。

Step 3: 解式(8)，求状态量，并取其中绝对值最大者。

Step 4: 计算式(9)，检查是否达到收敛标准。

Step 5: 若未达到收敛标准，则修改状态量式，令 和，返回Step 2继续迭代求解，直到结果收敛为止。

Step 6: 进行不良数据的检测与辨识。将量测残差进行加权计算，得到加权残差r_w；计算加权残差灵敏度矩阵 ；设定阈值，通过假设检验测出是否存在残差，并利用残差搜索对不良数据进行辨识。

2.3  具有反馈数据丢包的无功状态估计算法流程

针对网络化控制无功优化系统中反馈数据丢包而造成某些状态量不可测的情况，以文献[17]中改进差分进化算法为例讨论无功优化算法流程的改进。当存在不可测反馈状态量时，采用本文所提改进状态估计法，所得无功优化差分进化算法的具体流程如图3 所示。

图3  具有反馈数据丢包且改进后的无功优化进化算法流程

Fig.3  Flowchart of improved evolutionary algorithm for RPO with feedback data packet dropout

3  仿真算例与分析

为了验证所提出的状态估计方法对于网络化控制无功优化系统反馈数据丢包的有效性和可行性，分别采用IEEE14节点和IEEE30节点系统进行仿真实验。针对IEEE14节点系统对无功状态估计效果进行验证；对于IEEE30节点系统，结合进化差分算法验证所提出无功状态估计法的优化性能。IEEE14节点系统包括9个PQ节点和4个PV节点，待求的未知状态量为26个；IEEE30节点系统包括24个PQ节点和5个PV节点，待求的未知状态量为58个。

在算法初始化阶段，IEEE14和IEEE30节点系统网络节点的电压相角均设为0，电压幅值均设为平衡节点的电压幅值1.06。IEEE30系统的节点电压上、下限分别为1.10 V和0.95 V，变压器变比上、下限分别为1.10和0.90，初始状态的有功网损值为17.557 MW，压降为6.193 V。在该无功优化仿真实验过程中，差分进化计算的代数设置为200，种群规模设置为50。

首先，采用前述加权最小二乘法作为反馈状态的估计算法，应用于IEEE14节点系统进行估计性能的分析。将状态估计运算后所得数据与未进行状态估计直接由无功控制器接收的数据进行对比，如表1所示。从表1可知：在网络化控制无功优化系统中，由于存在网络传输时延和反馈数据丢包，导致系统4和13节点电压与5，9和10节点相角发生较大误差。采用本文提出的状态估计方法，利用已接收的网络传输反馈量进行状态估计，比较估计运算前后的结果：由于系统反馈回路发生数据丢包，在未采用任何处理时，无功调节控制器所接收的数据与真实值相比误差较大，特别是相角差距更远；而采用状态估计进行补偿后，估计结果与真值比较接近，不仅可以很好地纠正幅值误差，也较好地弥补了相角较严重的偏离。这表明本文提出的状态估计法可以较好地解决反馈回路数据丢包的问题。

为了进一步验证状态估计法应用于具有反馈数据丢包的网络化控制无功优化系统的优越性，还采用IEEE30节点系统进行仿真实验。设定反馈通道中具有不同数目的状态量存在数据丢包情况(即具有相应不同数目的不可测状态量，并用C表示)，实验中节点分别取4和8，采用基于状态估计的改进差分进化算法进行处理，其网损和压降的仿真对比结果分别如图4和图5所示。从图4和图5可以看出：(1) 不可测状态数目会影响系统的无功优化性能，不可测数越多，系统性能越差；(2) 采用本文状态估计改进算法后，可以改善反馈通道数据丢包所致的状态变量不可测问题，使得系统的无功优化性能提高；(3) 无论状态量丢失数目，采用状态估计处理后的系统性能均能达到较优状态；(4) 随着不可测状态数目的增加，该优化算法的收敛性能所下降。

表1  IEEE 14系统估计结果的对比

Table 1  Comparison of before and after estimation to IEEE14 system

图4  IEEE 30系统无丢包、未采用及采用状态估计算法的网损曲线

Fig.4  Power loss curves of ideal, without and with state estimation algorithm to IEEE30 system

图5  IEEE 30系统无丢包、未采用及采用状态估计算法的压降曲线

Fig.5  Voltage drop curves of ideal, without and with state estimation algorithm to IEEE30 system

4  结论

(1) 针对网络传输等引起网络化控制无功优化系统中反馈状态变量发生的数据丢包问题，提出采用接收缓存器以改进状态估计算法。该算法不仅可以有效处理系统中发生的状态变量丢包问题，较好地纠正了由丢包引起的状态量缺失和误差；还可将估计结果引入后续的无功优化计算过程中，提高了系统的优化性能。

(2) 网络化控制无功优化系统中状态变量发生丢失将极大影响原有系统的优化性能，且状态变量丢失越多，系统性能会越差；而采用状态估计处理后，可以较好地进行数据补偿，提高原有优化算法的性能；在状态变量丢失较少的情况，丢包处理后的系统性能甚至可以接近无丢包系统的性能。

参考文献：

[1] 彭可, 黄丹, 罗安. 基于网络化控制模型的改进无功优化算法[J]. 电网技术, 2011, 35(3): 103-107.

PENG Ke, HUANG Dan, LUO An. An improved reactive power optimization algorithm based on networked control model[J]. Power System Technology, 2011, 35(3): 103-107.

[2] 彭可, 盘清琳, 李仲阳, 等. 网络化控制多目标无功优化的进化算法[J]. 中南大学学报: 自然科学版, 2012, 43(8): 3073-3079.

PENG Ke, PAN Qinglin, LI Zhongyang, et al. Evolutionary algorithm for network-controlled multi-objective power optimization[J]. Journal of Central South University: Science and Technology, 2012, 43(8): 3073-3079.

[3] Mesut B, McDermott T E. Distribution system state estimation using AMI data[C]// Proceedings of IEEE Power Systems Conference and Exposition. Seattle, PA, USA: IEEE, 2009: 1-3.

[4] Lefebvre S, Prévost J. Topology error detection and identification in network analysis[J]. International Journal of Electrical Power and Energy Systems, 2006, 28(5): 293-305.

[5] 吴杰, 卢志刚, 杨斌, 等. 基于改进并行遗传算法的电网状态估计[J]. 电网技术, 2006, 30(18): 64-68.

WU Jie, LU Zhigang, YANG Bin, et al. Power network status estimation based on improved parallel genetic algorithm[J]. Power System Technology, 2006, 30(18): 64-68.

[6] de la Antonio V J, Romero P C, Expósito A G. Substation data validation by a local three-phase generalized state estimator[J]. IEEE Transactions on Power Systems, 2005, 20(1): 264-271.

[7] 黄彦全, 肖建, 李云飞, 等. 支持向量机在电力系统状态估计中的应用[J]. 中国电机工程学报, 2005, 25(25): 256-260.

HUANG Yanquan, XIAO Jian, LI Yunfei, et al. A state estimation for　power system using support vector[J]. Proceedings of the CSEE, 2005, 25(25): 256-260.

[8] 黄彦全. 电力系统状态估计若干问题的研究[D]. 成都: 西南交通大学电气工程学院, 2005: 1-18.

HUANG Yanquan. On some subjects in power system state estimation[D]. Chengdu: Southwest Jiaotong University. College of Electrical Engineering, 2005: 1-18.

[9] Zhang H S, Lu X, Cheng D Z. Optimal estimation for continuous-time systems with delayed measurements[J]. IEEE Transaction on Automatic Control, 2006, 51(5): 823-827.

[10] 王宝凤. 网络化控制系统中状态估计问题的研究[D]. 大连: 大连海事大学信息科学与技术学院, 2010: 40-57.

WANG Baofeng. Study for state estimation problems in networked control systems[D]. Dalian: Dalian Maritime University. College of Information Science and Technology, 2010: 40-57.

[11] 孙宏斌, 高峰, 张伯明, 等. 最小信息损失状态估计中潮流和拓扑统一估计的通用理论[J]. 中国电机工程学报, 2005, 25(17): 1-4.

SUN Hongbin, GAO Feng, ZHANG Boming, et al. Minimum information loss based state estimation: General theory for unified estimation of power flow and topology[J]. Proceedings of the CSEE, 2005, 25(17): 1-4.

[12] 张海波, 张伯明, 孙宏斌, 等. 电力系统状态估计可观测性分析中关于量测岛合并的理论分析[J]. 中国电机工程学报, 2003, 23(2): 46-49.

ZHANG Haibo, ZHANG Boming, SUN Hongbin, et al. Theory analysis about measurement islands’ combination in observability analysis in power system state estimation[J]. Proceedings of the CSEE, 2003, 23(2): 46-49.

[13] Shih K R, Huang S J. Application of a robust algorithm for dynamic state estimation of power systems[J]. IEEE Transactions Power Systems, 2002, 17(1): 141-147.

[14] 王珍意, 周良松, 张步涵. 基于降阶雅克比矩阵的电力系统状态估计可观测性分析方法[J]. 继电器, 2005, 33(10): 1-4.

WANG Zhenyi, ZHOU Liangsong, ZHANG Buhan. Observability analysis of power system state estimation based on reduced Jacobian matrix[J]. Relay, 2005, 33(10): 1-4.

[15] Korres G N. A robust algorithm for power system state estimation with equality constraints[J]. IEEE Transactions on Power Systems, 2010, 25(3): 1531-1541.

[16] 闫丽梅, 张士元, 任伟健, 等. 基于粒子群进化算法的电力系统状态估计研究[J]. 电力系统保护与控制, 2010, 38(2): 86-89, 95.

YAN Limei, ZHANG Shiyuan, REN Weijian, et al. Power system state estimation based on particle swarm optimization algorithm[J]. Power System Protection and Control, 2010, 38(2): 86-89, 95.

[17] 赵树本, 张伏生. 基于改进差分进化算法的电力系统最优潮流计算[J]. 电网技术, 2010, 34(8): 123-128.

ZHAO Shuben, ZHANG Fusheng. Solution of optimal power flow based on differential evolution and its modified algorithm[J]. Power System Technology, 2010, 34(8): 123-128.

(编辑  陈灿华)

收稿日期：2012-12-29；修回日期：2013-02-25

基金项目：湖南省自然科学基金资助项目(11JJ3080)；湖南省高校产业化培育项目(11CY012)；湖南省科技计划项目(2010CK3019)；湖南师范大学青年人才计划项目(ET51007)

通信作者：彭可(1973-)，男，湖南株洲人，博士，教授，从事网络化控制、电能质量治理、电力系统监控等研究；电话：13975804087；E-mail: pengk@tom.com

摘要：分析网络传输通道中通信时延、远动数据丢失对于电力无功优化的影响。针对由于时延与丢包等因素导致系统状态反馈变量出现误差和缺失的情况，提出一种具有反馈数据缓存的网络化控制无功优化改进算法。该算法在状态估计算法的基础上，引入接收缓存器对反馈通道中状态变量的缺失或误差进行修正，以保证无功优化运行时所需要的远程观测数据。采用差分进化算法，对于IEEE 14节点及IEEE 30节点系统进行仿真研究。研究结果表明：当网络化控制无功优化系统中反馈通道的量测数据出现缺失或误差时，利用改进后的状态估计方法可以较好地求出系统的状态量，并能应用于后续的相应无功优化计算过程，从而保证系统性能达到较优状态。