J. Cent. South Univ. Technol. (2011) 18: 2157-2162
DOI: 10.1007/s11771-011-0957-2![]()
Mechanical characteristics of columnar jointed rock at
dam base of Baihetan hydropower station
YAN Dong-xu(闫东旭)1, 2, XU Wei-ya(徐卫亚)1, 2, ZHENG Wen-tang(郑文棠)3, 4,
WANG Wei(王伟)1, 2, SHI An-chi(石安池)5, WU Guan-ye(吴关叶)5
1. Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering,Hohai University, Nanjing 210098, China;
2. Research Institute of Geotechnical Engineering, Hohai University, Nanjing 210098, China;
3. State Key Laboratory of Hydroscience and Hydraulic Engineering, Tsinghua University, Beijing 100084, China;
4. Guangdong Electric Power Design Institute, Guangzhou 510663, China;
5. East China Hydropower Investigation and Design Institute, Hangzhou 310014, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract:
Irregular columnar jointed structure is a primary irregular columnar morphological tensile fracture. In order to study the geometric features of irregular columnar joints and the new problems in geotechnical engineering, hydraulic and hydropower engineering caused by columnar jointed basaltic mass, Voronoi graph from geometry was introduced to simulate the irregular columnar jointed basaltic mass at Baihetan hydraulic station. Discrete element software UDEC was used to simulate the whole process of rigid bearing plate test. Anisotropic constitutive of columnar joints was adopted to analyze the stress diffusion of rock mass at dam base of Baihetan. The results show that, the compaction property and hysteresis effect are well simulated based on discrete element simulation of Voronoi joint structure by UDEC. Four stages of cyclic loading and unloading process are imaged clearly. The results from in situ rigid bearing plate tests are explicated and the stress diffusion rule of anisotropic body is affected by structure surface. The elements in the stress state of 4-5 MPa are the most, about more than 35% of the total. Appropriate constitutive must be proposed to columnar jointed rock mass with different styles. It has important significance to realize the nonlinear mechanical behavior of irregular columnar jointed basaltic mass.
Key words:
1 Introduction
Columnar jointed structure is a primary columnar morphological tensile fracture. It is common in volcanic lava, dried flour, clotted ice, epidermal cells under leaf, quenched metal and quenched glass. Reports of columnar joint in volcanic lava can be traced back to 1693 while Bulkeley described the Giant’s Causeway in Ireland. M?LLER [1] and GOEHRING et al [2] found that flour with a certain humidity in the process of drying, evaporation and diffusion of vapor, and heat spread of lava flows are in the similar process. Their results show that flour in the appropriate temperature will form a stable columnar fracture which is analogous with columnar jointed basalt. COLE [3] found that columnar fracture often occurs in clotted ice. FRENCH [4], HULL and CADDOCK [5] found that columnar fracture also exists in quenched metal and quenched glass. Reports about columnar joint in geological rock mass are generally in basic hypabyssal rock or eruptive rock (for example, basalt) [6-7].
Widely distributed columnar basalt lava gave birth to the environment of columnar joints, which brought up many well-known landscapes of columnar joints. On the other hand, this special jointed rock mass has also led to new engineering problems in geotechnical engineering and hydraulic and hydropower engineering. For example, at the Permian continental flood basalt in southwest China, generally the Emeishan basalt is one of the main foundation rocks in this region. Some hydropower stations are based on developed columnar jointed basalt. As a result, it is of great significance for hydropower project construction to study the engineering mechanical properties of columnar jointed rock mass. Discrete element software UDEC was used to simulate the whole process of rigid bearing plate test. Anisotropic constitutive of columnar joints was adopted to analyze the stress diffusion of rock mass at the dam base of Baihetan hydropower station.
2 Numerical analysis of irregular columnar joints
2.1 Voronoi graph in columnar jointed rock mass
Irregular columnar joint is a natural phenomenon. Because of its unique polygonal feature, it can be regarded as a Voronoi graph geometrically. It was VORONOI who first studied the characteristics of this mathematic figure systematically. As the Voronoi diagram is very similar to the natural structures of a lot of columnar joints, the numerical method of Voronoi joint network can be used to analyze the mechanical behaviors of irregular columnar joints. As it is of great difficulty to build a large number of columnar joints in continuum mechanics, finding exact mechanical constitutive of columnar joints is also awkward. For the past few years, mechanical behavior by simple contact with a large number of micro-elements under the surface of the macro-mechanical characteristics has emerged to reveal the complex mechanical behavior of new methods—DDA [8-9], discrete element [10-11], cellular automata [12-13], and the numerical simulation provides a new way to columnar joints.
The discrete element method of non-continuum numerical method, which relies on its absolute advantages in simulating a large number of joints, becomes the first choice in numerical analysis of columnar joints. Furthermore, its representative commercial softwares, UDEC and 3DEC, have been widely used internationally. UDEC has a strong capability of joints fracture network simulation [14]. The built-in Voronoi [15-16] tessellation generators can be the generation of Voronoi joint network automatically. Its deformable solution of discrete element model can not only simulate the embedding, contact, rotation and separation of columnar jointed basalt, but also use finite difference element to cut the rigid block. Then, the elastic deformation and the internal stress distribution of rock mass are calculated. This test uses UDEC to simulate the rigid bearing plate of the columnar jointed basalt.
2.2 Simulation test of irregular columnar joints
In a area of 6 m × 2 m, the average length edge equaled to 0.2, the number of iterations was less than 100 to control the cylinder shape (mostly quadrangle and pentagon). The numerical model of columnar joints at Baihetan hydropower station is shown in Fig.1. There is serial number in Fig.1 created by automatic UDEC for controlling operation order. UDEC can not only simulate the contact behavior of joints with proper joint constitutive, but also cut the block into units to calculate the stress and strain; as a result, it can simulate the numerical bearing plate test well.
The diameter of the numerical bearing plate was 2.0 m. Considering the boundary effect, the length of the cylinder model took the value of 6 m according to Ref.[17], and the max applied load was 10 MPa. The physical and mechanical parameters of the basalt took the average of laboratory test, the geometric parameters of columnar joints were obtained from elaborate geologic mapping, and the mechanical parameters of the columnar joints were obtained from inversion of in situ test (Table 1). The test was conducted in three stages. Pressure of 0-2 MPa was applied in the initial compaction stage, considering the joint disturbed parameter of 0.5. Pressure of 2-10 MPa was applied in the subsequent loading stage while the stiffness of the joints was restored to measured value. Loading every 2 MPa and calculating the balance, the unloading test was conducted in every 2 MPa until the loading was zero. When every loading and unloading test was over, the average stress and vertical displacement of the columnar jointed rock mass near the center bottom of the bearing plate were collected with fish command stream. As shown in Fig.2, the results are arrayed. Then, the stress-displacement curves are drawn in Fig.3.

Fig.1 Described cylindrical map at Baihetan hydraulic station and UDEC numerical model of deformed columnar joints
Table 1 Irregular columnar joint parameters at Baihetan hydraulic station in UDEC calculation

Numerical simulations show that, the stress- displacement curve of Voronoi columnar joints numerical test is in accordance with the law of in-situ test result. The curve consists of four stages, the slope of the initial pressure consolidation stage is less than that of the loading stage, and the slope of the subsequent unloading stage is less than that of the initial unloading stage. By comparing the deformation in four stages and permanent deformation after unloading of in-situ test and numerical test, the deformations are both in the magnitude of 10-4 m. It is also shown that the initial unloading stage (Slope III in Fig.3) of the numerical test is composed of three multi-line curves with decreasing slope (1, 2 and 3 in Fig.3), and this curve matches the initial unloading curve of in-situ test well [18].
3 Analysis of anisotropic stress diffusion of columnar jointed rock mass at Baihetan hydropower station
The deadweight of dam and the water pressure are distributed to base and abutment through arch-beam. This is equivalent to the problems of stress transmission and settlement distribution, which are caused by half plane foundation loaded by ground surface. The rule of stress transmission is different from isotropic medium obviously because of jointed rock.
BOUSSINESQ [19] obtained stress distributions of every point in half plane which is composed of isotropic elastic medium and concentrated load:
![]() (1)
(1)
CONWAY and ITHACA [20-21] deduced the analytical solution of stress distribution of orthotropic half-plane rock which is affected by compressive stress and shearing stress. GOOOMAN [22] extended the analytical solution of stress distribution of orthotropic half-plane with different joint tendency α and inclined linear load:
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
where β=θ-α, E is elastic modulus and ν is Poisson ratio of rock block. Kn and Ks are normal stiffness and shearing stiffness. S is the average spacing of discontinuous surface. X is the component of linear load parallel to the joint surface and Y is the component vertical to the joint surface.
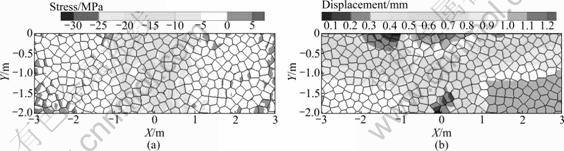
Fig.2 Stress (a) and displacement (b) nephograms of plate loading test of Voronoi columnar joint
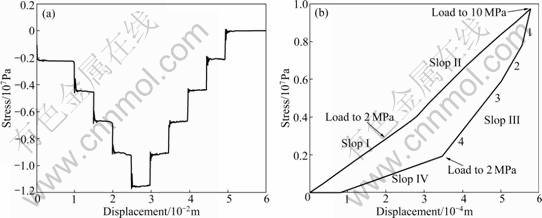
Fig.3 Curve of stress and displacement from numerical bearing plate test on columnar jointed basalt by Voronoi: (a) Tensile loading process; (b) Compressive loading process
The fault structure at dam site of Baihetan hydropower station is very developed. The geological structure types include different levels of layered dislocation band, inner dislocation band, control fault, structural fissure and wild joints [18]. Considering different sizes and control ranges of structural plane at different levels, there are different ways to simulate the structural plane. The level and the dimension of structural plane disclosed in rock mass are also different in different scales. While the stability of large area (Baihetan dam site area) is analyzed, the effect of large structural fault must be paid attention to, which decides the location of the dam. While the stability of underground cavern and high slope is analyzed, the fracture of level III must be considered. The effect of columnar joints in level IV and microfissure in level V must be thought over for in-situ test and laboratory test. The numerical analysis methods considering the scale effect can be divided into two categories: the equivalent continual mechanical analysis of complex constitutive in large scale plus simple rock structure and non-continual mechanical analysis of simple constitutive in small scale plus complex rock structure. The former is emphasized on the deformation and destructive rule of large-scale macroscopic rock mass, while the latter can be used to simulate the nonlinear property of joints indicated by laboratory test and in-situ test, such as hysteresis effect, strain hardening, strain softening, fracture propagation, and progressive failure. It is difficult to describe accurately even by a complex constitutive.
Columnar jointed rock mass is composed of complete rock and intensively and regularly distributed joints, which can be simulated by elastoplastic body (rock mass) and cutting plane (joints). However, in large areas of numerical analysis of jointed rock mass (for example the rock mass of dam base and abutment, whose size is large than 100 m × 100 m × 100 m), it is unrealistic to construct numerical model and quicken numerical calculation according to the size of structure surface of 0.2 m × 0.2 m × 1.0 m completely because of dense cutting. However, dealing with the high jointed rock mass by mechanical equivalent principle before numerical simulation, and considering the size effect (REV) [23-24], rock mass can be simulated by degenerated continuous anisotropic body. Thus, the anisotropy of rock mass is shifted to constitutive parameter. Not only the anisotropy of columnar joints is retained, but also the difficulties in numerical model are avoided.
Because the strength of jointed rock, especially thick fracture zone, is lower than that of surrounding rock, asymmetric deformation and settlement are frequent at dam abutment of both sides under the force created by arch abutment and arch base. Then, the stress of dam will be redistributed and the local stress concentration and tensile stress will affect the stability of arch dam and abutment. Therefore, systematic study is significant to anisotropic stress diffusion of arch dam-dam and base-dam abutment rock mass system.
The stress diffusion capacity of columnar jointed rock and the impact to the arch dam were analyzed by software FLAC3D. In the calculation models, non-columnar jointed rock was analyzed by Mohr-Coulomb constitutive with tensile yield, but structural plane was analyzed by Mohr-Coulomb constitutive without tensile yield. Columnar joints were analyzed by orthotropic elastic constitutive with anisotropic Mohr-Coulomb yield criterion combined with different space principal axes.
As listed in Table 2, under the condition of normal water level without reinforcement, the main stress of columnar jointed rock foundation calculated by isotropic constitutive is 3-5 MPa. The columnar jointed rock foundation elements under the stress of 3-4 MPa and 4-5 MPa are about 36.19% and 46.17% in the number of total elements in selected zone. The ratios of volume are about 28.70% and 40.92%. The ratios of elements calculated by anisotropic constitutive under the stress of 3-4 MPa and 4-5 MPa are 36.10% and 36.02%. The ratios of volume are about 29.38% and 32.93%. It is shown that with the anisotropic constitutive, elements under the stress of 3-4 MPa and 4-5 MPa are reduced and transferred to the 5-6 MPa stress range. The ratios are reduced by 2.94% and 3.55%, respectively. The tensile stresses under anisotropic constitutive are increased by 0.32% and 0.41%. It is indicated that the maximum principal compressive and tensile stresses of dam base with anisotropic constitutive increase. According to the distribution of compressed elements of each stress range, the tensile elements increase under anisotropic constitutive in the upstream face where columnar joints rock foundation and fault F16 intersect. From Fig.4, the elements under the stress larger than 6 MPa increase obviously at the junction of columnar jointed rock foundation and the LS331 inner dislocation band. Because of the anisotropic constitutive and yield criterion, the inner dislocation band in columnar jointed rock is weak in shearing property. Columnar jointed rock mass is weaker in shearing property under anisotropic yield criterion than isotropic constitutive. It is shown that the strength of columnar jointed rock foundation is mainly controlled by inner dislocation band.
Table 2 Percentage of element number and volume in some stress interval

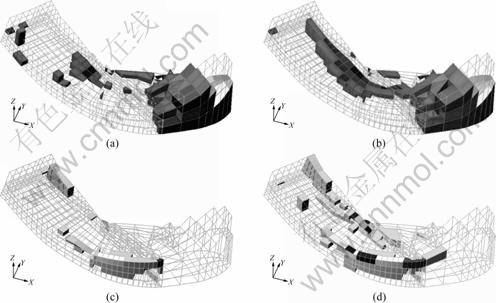
Fig.4 Visualized stress state of different constitutives of columnar jointed mass in dam base: (a) Isotropic constitutive under stress of 6-10 MPa; (b) Anisotropic constitutive under stress of 6-10 MPa; (c) Isotropic constitutive under stress of 0-3 MPa; (d) Anisotropic constitutive under stress of 0-3 MPa
4 Conclusions
1) The basic geometrical features of columnar jointed structure were analyzed and Voronoi graph was employed to simulate the irregular columnar jointed basalt at Baihetan hydropower station. The numerical simulation of UDEC proves four stages of loading and unloading curve: the initial consolidation phase, the loading phase, the initial unloading rebound deformation stage and the subsequent unloading slip stage.
2) The UDEC numerical test based on the Voronoi joint network can simulate the loading and unloading mechanic characteristics of irregular columnar jointed rock. It can explain the significant compaction and hysteresis loop effect in the rigid bearing plate test of columnar jointed rock mass.
3) Restricted by the two-dimensional model, the hysteresis loop effect is only analyzed in the vertical load direction. Study of next step can be set from the three- dimensional Voronoi model to research the hysteresis loop effect of columnar joints.
4) The stiffness of joints in numerical bearing plate test except the initial pressure consolidation stage is treated as a constant. This means that joint constitutive is ideal elasto-plastic (Mohr-Coulomb face contact behavior). Therefore, the stress-displacement curve of subsequent loading stage is a straight line, while it is a slightly concave curve in the in-situ test. This is caused by the confining pressure influencing on the stiffness of columnar joints. The stiffness of joint under high confining pressure has a significant characteristic of strain hardening. As a result, it is more suitable to employ continuous yielding joint constitutive.
5) The calculations show that the maximum principal compressive stress and tensile stress increase under anisotropic constitutive. The stress diffusion rule of anisotropic body is affected by structure surface. The anisotropy of columnar joints is not the dominant factor for the stability of the dam site. The strength of columnar jointed rock foundation is affected by inner disturbed belts mainly. The above facts show that columnar jointed rock foundation in columnar mosaic block structure, which is distributed in dam base and bears the arch weight and water load, is able to be reduced to isotropic Mohr-Coulomb material. It is more accurate to consider Hoek-Brown constitutive under the strengthening effect of confining pressure to mechanical property of joints. However, the columnar jointed rock mass disturbed by underground excavation and columnar jointed rock mass in columnar mosaic block structure which is affected by excavation relaxation and weather unloading are anisotropic obviously. It is more appropriate to adopt anisotropic constitutive to them.
References
[1] M?ELLER G. Experimental simulation of basalt columns [J]. Journal of Volcanology and Geothermal Research, 1998, 86(4): 93-96.
[2] GOEHRING L, MAHADEVAN L, MORRIS S W. The dynamic similarity between columnar joints in basalt and starch [C]// American Geophysical Union Fall Meeting. San Francisco, 2007: 651-658.
[3] COLE D M. Crack nucleation in polycrystalline ice [J]. Cold Regions Science and Technology, 1988, 15(1): 71-79.
[4] FRENCH J W. The fracture of homogeneous media [J]. Trans Geol Soc Glasgow, 1925, 17(1): 50-58.
[5] HUL D, CADDOCK B D. Simulation of prismatic cracking of cooling basalt lava flows by the drying of sol-gels [J]. Journal of Materials Science, 1999, 34(23): 57-67.
[6] LI Jin-long, WANG Pu-jun, ZHENG Chang-qing, TANG Hua-feng, WU Yan-xiong, BIAN Wei-hua. Characteristics and genesis of rhyolite with columnar joints from the yingcheng formation in southeastern uplift of the songliao basin [J]. Journal of Jilin University: Earth Science Edition, 2007, 37(6): 56-62. ( in Chinese)
[7] SHAN Zhi-qiang. In search of pillars around China [J]. Chinese National Geography, 2009, 586(8): 32-64. (in Chinese)
[8] GRAYELI R, HATAMI K. Implementation of the finite element method in the three-dimensional discontinuous deformation analysis (3D-DDA) [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32(15): 1883-1902.
[9] YANG M, FUKAWA T, OHNISHI Y, NISHIYAMA S, MIKI S, HIRAKAWA Y, MORI S. The application of 3-dimensional DDA with a spherical rigid block for rockfall simulation [J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(Supp1): 251-256.
[10] FENG Y T. On the central difference algorithm in discrete element modeling of impact [J]. International Journal for Numerical Methods in Engineering, 2005, 64(14): 1959-1980.
[11] LI Yan, LIU Shao-jun, YU Hong-yun. Dynamic analysis of deep ocean mining system based on multi rigid body discrete element model [J]. Journal of Central South University of Technology, 2006, 37(4): 742-747. (in Chinese)
[12] MORENO N, WANG Fang, MARCEAU D J. Implementation of a dynamic neighborhood in a land-use vector-based cellular automata model [J]. Computers, Environment and Urban Systems, 2009, 33(1): 44-54.
[13] CHO H, SWARTZLANDER J. Adder and multiplier design in quantum-dot cellular automata [J]. IEEE Transactions on Computers, 2009, 58(6): 721-727.
[14] Itasca Consulting Group. UDEC User’s guide [M]. Minneapolis, Minnesota: Itasca Consulting Group Inc, 2006: 24-30.
[15] AICHHOLZER O, AIGNER W, AURENHAMMER F, HACKL T, JUTTLER B, PILGERSTORFER E, RABL M. Divide-and-conquer for Voronoi diagrams revisited [J]. Computational Geometry: Theory and Applications, 2010, 43(8): 688-699.
[16] KLEIN R, LANGETEPE E, NILFOROUSHAN Z. Abstract Voronoi diagrams revisited [J]. Computational Geometry: Theory and Applications, 2009, 42(9): 885-902.
[17] MENG Guo-tao. Geomechanical analysis of anisotropic columnar jointed rock mass and its application in hydropower engineering [D]. Nanjing: Hohai University, 2007: 68-79. (in Chinese)
[18] East China Investigation and Design Institute. Engineering geology’s research report of columnar jointed basalt at Baihetan hydropower station on Jinsha River [R]. 2006. (in Chinese)
[19] BOUSSINESQ J. Application research of elastic solid movement and balace potential [M]. Paris: Gauthier-Villars, 1885. (in French)
[20] CONWAY H D, ITHACA N Y. Some problems of orthotropic plane stress [J]. Journal of Applied Mechanics, 1953, 20(1): 72-76.
[21] CONWAY H D, ITHACA N Y. Note on the orthotropic half space subjected to concentrated loads [J]. Journal of Applied Mechanics, 1955, 77(3): 130-135.
[22] GOODMAN R E. Introduction to rock mechanics [M]. New York: Wiley, 1989: 576-583.
[23] CHEN S H, FENG X M, ISAM S. Numerical estimation of REV and permeability tensor for fractured rock masses by composite element method [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32(12): 1459-1477.
[24] ESMAIELI K, HADJIGEORGIOU J, GRENON M. Estimating geometrical and mechanical REV based on synthetic rock mass models at Brunswick Mine [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(6): 915-926.
(Edited by YANG Bing)
Foundation item: Projects(50979030, 50911130366) supported by the National Natural Science Foundation of China; Project(2009B14014) supported by the Fundamental Research Funds for the Central Universities in China
Received date: 2010-11-10; Accepted date: 2011-03-14
Corresponding author: YAN Dong-xu, PhD; Tel: +86-25-83787037; E-mail: yandongxuu@qq.com
Abstract: Irregular columnar jointed structure is a primary irregular columnar morphological tensile fracture. In order to study the geometric features of irregular columnar joints and the new problems in geotechnical engineering, hydraulic and hydropower engineering caused by columnar jointed basaltic mass, Voronoi graph from geometry was introduced to simulate the irregular columnar jointed basaltic mass at Baihetan hydraulic station. Discrete element software UDEC was used to simulate the whole process of rigid bearing plate test. Anisotropic constitutive of columnar joints was adopted to analyze the stress diffusion of rock mass at dam base of Baihetan. The results show that, the compaction property and hysteresis effect are well simulated based on discrete element simulation of Voronoi joint structure by UDEC. Four stages of cyclic loading and unloading process are imaged clearly. The results from in situ rigid bearing plate tests are explicated and the stress diffusion rule of anisotropic body is affected by structure surface. The elements in the stress state of 4-5 MPa are the most, about more than 35% of the total. Appropriate constitutive must be proposed to columnar jointed rock mass with different styles. It has important significance to realize the nonlinear mechanical behavior of irregular columnar jointed basaltic mass.


