J. Cent. South Univ. (2016) 23: 1525-1534
DOI: 10.1007/s11771-016-3204-z
Microstructure modeling and virtual test of asphalt mixture based on three-dimensional discrete element method
MA Tao(马涛)1, 2, ZHANG De-yu(张德育)3, ZHANG Yao(张垚)1,
ZHAO Yong-li(赵永利)1, HUANG Xiao-ming(黄晓明)1
1. School of Transportation, Southeast University, Nanjing 210096, China;
2. Department of Civil and Environmental Engineering, Rutgers, the State University of New Jersey, NJ, 08854, USA;
3. School of Civil Enginerring and Architecture, Nanjing Institute of Technology, Nanjing 211167, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract:
The objective of this work is to model the microstructure of asphalt mixture and build virtual test for asphalt mixture by using Particle Flow Code in three dimensions (PFC3D) based on three-dimensional discrete element method. A randomly generating algorithm was proposed to capture the three-dimensional irregular shape of coarse aggregate. And then, modeling algorithm and method for graded aggregates were built. Based on the combination of modeling of coarse aggregates, asphalt mastic and air voids, three-dimensional virtual sample of asphalt mixture was modeled by using PFC3D. Virtual tests for penetration test of aggregate and uniaxial creep test of asphalt mixture were built and conducted by using PFC3D. By comparison of the testing results between virtual tests and actual laboratory tests, the validity of the microstructure modeling and virtual test built in this study was verified. Additionally, compared with laboratory test, the virtual test is easier to conduct and has less variability. It is proved that microstructure modeling and virtual test based on three-dimensional discrete element method is a promising way to conduct research of asphalt mixture.
Key words:
1 Introduction
The mechanical behavior of asphalt mixture has important influence on the field performance of asphalt pavement. Understanding the mechanical behavior of asphalt mixture is a critical step to design asphalt mixture and asphalt pavement with satisfied performance [1]. Previous studies referring to mechanical behavior of asphalt mixture were mainly based on laboratory experimental tests. However, it is difficult to control the variability of experimental tests due to complex artificial and environmental interferences. More importantly, it is difficult to build relationships between macro-properties and micro-structure of asphalt mixture based on experimental tests. Thus, it is difficult to understand the mechanical fundamentals of asphalt mixture from experimental tests. Meanwhile, most of the experimental approaches are time-consuming and involve considerable labor efforts and financial cost. Therefore, micromechanical modeling and virtual test were developed to solve the previous problems and to characterize asphalt mixture for both material evaluation and structural design purpose.
Currently, finite element method (FEM) and discrete element method (DEM) are two major numerical methods employed to characterize the mechanical behavior of asphalt mixture. Based on continuum- damage theory and/or fracture mechanics, the FEM method has been successfully used to investigate the mechanical properties of asphalt mixture. For example, it can well capture the stress-strain distribution within asphalt mixture to analyze the stiffness anisotropy, fracture property and deformation behavior of asphalt mixture [2-5]. To capture the heterogeneity and microstructure of asphalt mixture, FEM models were studied to build the random aggregate structures of asphalt mixture [6-7]. It is proved that FEM model with random aggregate structures can well characterize the irregular shape and angularity of coarse aggregates within asphalt mixture [8]. However, FEM models with random aggregates structures for asphalt mixture are still based on continuum theory. It is difficult to them to characterize the contact and sliding behavior between aggregates and the bonding behavior between aggregate and asphalt mastic. Meanwhile, FEM still has difficulties to generate three-dimensional random aggregate structures [9]. The DEM method initially developed by CUNDALL and STRACK [10] provides another promising way to model and characterize the micromechanical behavior of asphalt mixture. Compared with FEM, it is easier for DEM to build three- dimensional coarse aggregates. And DEM has advantages in characterizing the discontinuous characteristics and large deformational behavior of asphalt mixture by modeling the contacts between different ingredients of asphalt mixture. In the past decades, different DEM procedures and micromechanical models for DEM have been developed [11-14].Based on DEM methods, many studies have been conducted to characterize the mechanical properties of asphalt mixture, such as fracture behavior, viscoelastic deformation and dynamic stiffness [15-18].
However, most of the previous researches are based on two-dimensional models which cannot well characterize the interlock effect within aggregates and the three-dimensional skeleton of asphalt mixture. More importantly, either highly idealized models or image-based models are mainly used in previous studies. The highly idealized models cannot accurately depict the microstructure of asphalt mixture, especially the aggregate skeleton leading to obvious simulating errors. The image-based models can well describe the microstructure of asphalt mixture. However, they highly rely on the complex image-processing technique and testing equipment. Furthermore, for DEM method with image-based models, real asphalt mixtures need to be prepared and scanned to build digital samples for DEM modeling. Thus, the previous problems of experimental test, such as expensive equipment, considerable manpower and artificial interferences, show again in the image-based DEM method.Therefore, new three-dimensional DEM model to characterize the microstructure of asphalt mixture without image processing technique was developed in this study. And virtual tests based on a commercial discrete element software referred to as Particle Flow Code in three dimensions (PFC3D) were built and conducted to verify the feasibility of the developed microstructure modeling and simulation of asphalt mixture.
2 Experimental and methodology
2.1 Materials
A reference asphalt mixture with type, of AC13 was designed according to Chinese Standard Specification [19]. The gradation is shown in Table 1 and the asphalt content is 4.9%. This reference asphalt mixture was used in the following laboratory tests and the virtual modeling and tests.
It is considered that coarse aggregates larger than 2.36 mm form the main skeleton of asphalt mixture and asphalt mastic composed of aggregates smaller than 2.36 mm (including filler) as well as asphalt binder mainly provide bonding action by filling in the skeleton void [20]. With consideration of the computing efficiency of PFC3D, during virtual modeling and test, asphalt mixture is regarded as a three-phase material: coarse aggregates (larger than 2.36 mm), asphalt mastic (a combination of fine aggregates and asphalt) and air voids. The gradation of the coarse aggregates for the designed asphalt mixture is shown in Table 2. The gradation of asphalt mastic for the designed asphalt mixture is shown in Table 3 and its asphalt content is determined to be 11.9%.
Table 1 Gradation of designed asphalt mixture

Table 2 Gradation of coarse aggregates

Table 3 Gradation of asphalt mastic

2.2 Laboratory tests
Penetration test by using Universal Testing Machine (UTM) was designed to characterize the inner frictional resistance of coarse aggregates. Coarse aggregates were prepared according to the gradation in Table 2 and then put into a cylindrical mould. After being vibrated by vibrating platform, loading board with pressure of 10 kN was applied to further compact the testing aggregates. During penetration test, a cuboid penetration rod was penetrated into the testing sample at a speed of 1 mm/min. The penetration resistance along with the penetration depth was recorded.
The uniaxial creep test by UTM according to Chinese standard specification [21] was conducted for the designed asphalt mixture. The testing temperature was 60 °C and the applied axial stress was 0.4 MPa. During trial tests by current testing procedure, it was found that, when the load was applied to the sample, an instantaneous displacement about 4 cm was generated by the loading board and it is difficult for the applied load to reach the target value immediately. It influenced the accuracy of laboratory test and caused operative error between laboratory test and virtual test. To fix the previous problem, the current loading procedure was modified to get accurate testing results. As shown in Fig. 1, during the modified uniaxial creep test, a preload of 5 kPa was applied for 20 s and then the load was immediately increased to the required testing load for 200 s.
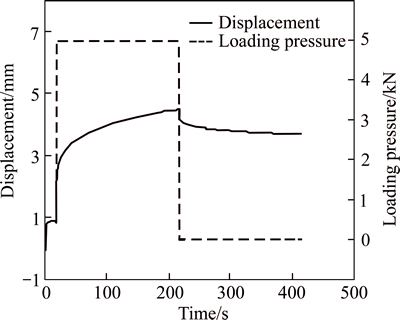
Fig. 1 Modified loading mode for uniaxial creep test
2.3 Basic methodology for virtual modeling
As shown in Fig. 2, in the modeling procedure of PFC3D, the basic principle is that material is discrete as balls with contacts [22]. In Fig.2, Un is the overlap of the two balls; d is the distance between the ball centers; R[A] is the radius of the ball A; R[B] is the radius of the ball B; xi[A] is the position vector of the center of ball A; xi[B] is the position vector of the center of ball B; x[C] is the contact point of the ball-ball contact model; ni is a unit normal vector that is directed along the line defining the shortest distance between the ball centers. For asphalt mixture, coarse aggregates are discontinuous and each coarse aggregate particle can be modeled by using a clump of balls. Asphalt mastic is considered as a continuum media and can be modeled by using uniformly sized balls contacting with each other. Some of the mastic discrete elements can be removed to get target air voids in asphalt mixture. The critical points to model asphalt mixture are the modeling of graded coarse aggregates and set up accurate mechanical contacts within the same ingredient and between different ingredients.
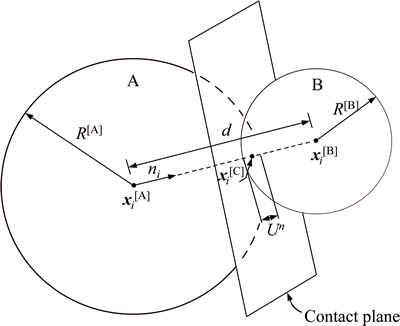
Fig. 2 Balls set with contact
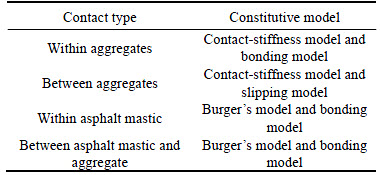
PFC3D provides three basic constitutive models to define the mechanical contacts between balls which are stiffness model, slipping model and bonding model. Stiffness model describes the deformation behavior at a contact which indicates the relationship between the relative displacement and the contact force at a contact. Slipping model and bonding model describe the strength properties at a contact. The bonding model provides tensile and shear strengths at a contact while the slip model provides no tensile strength and allows slip to occur when limiting shear force is reached. Based on previous researches [23-25], Table 4 lists the contacts within asphalt mixture and the corresponding constitutive models usually used at different contacts.
Table 4 Contacts within asphalt mixture and corresponding constitutive models
3 Microstructure modeling
3.1 Modeling of aggregate particle
3D shape of aggregate has important effects on the mechanical behavior of asphalt mixture. Previous studies proved that aggregates can be simplified as irregular polyhedron [26]. Thus, a randomly generating algorithm was built to capture the 3D irregular shape of aggregate. The basic steps of the randomly generating algorithm are summarized as follows:
1) A cube with side length equaling the aggregate size is built based on Eq. (1).
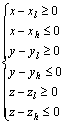 (1)
(1)
where xl, xh, yl, yh, zl, zh are boundary values for the surfaces of the cube.
2) Based on the center of the cube, a ball with radius R smaller than the side length of the cube is created inside the cube by Eq. (2).
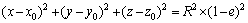 (2)
(2)
where (x0, y0, z0) is the center coordinates of the cube and the ball; R is the radius of the ball; e is random number within 0 and 1 to control the radius of the generated balls.
3) Several points are randomly generated on the surface of the ball according to Eqs. (3) and (4).
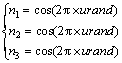 (3)
(3)
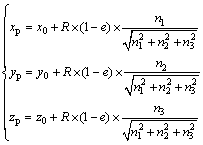 (4)
(4)
where urand is random number within 0 and 1; n1, n2 and n3 are randomly generated numbers; (xp, yp, zp) are the coordinates of the randomly generated point.
4) Based on the normal vectors determined by the ball center and the random points generated in the previous steps, several planes are randomly generated based on Eq. (5).
 (5)
(5)
5) By using the generated random plans to cut the cube, an irregular polyhedron particle is generated as shown in Fig. 3. And the controlling equation for the irregular polyhedron particle is shown as Eq. (6).
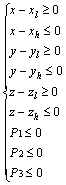 (6)
(6)
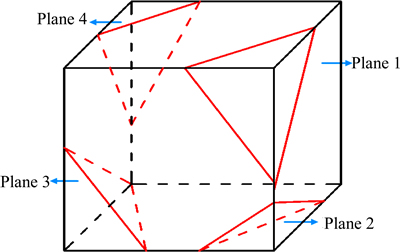
Fig. 3 Irregular polyhedron particle generation
Based on the randomly generating algorithm, modeling procedure was built based on PFC3D to generate coarse aggregates. Figure 4 shows the basic generating steps in PFC3D. Table 5 shows examples of randomly generated coarse aggregates with different sizes. It can be seen that, although the virtual aggregates are not exactly the same with the real aggregates shown in Fig. 5, it can well characterize the various 3D irregular shape property of real aggregates.
3.2 Modeling of graded aggregates
During modeling of PFC3D, it is considered that the graded aggregates have random distribution in asphalt mixture. And to generate graded aggregates, the volumetric gradation of aggregates needs to be determined based on the mass gradation. Thus, a converting algorithm was proposed to calculate the volumetric gradation of aggregates based on the following steps.
1) For designed asphalt mixture and specific test, the total volume of the test sample, asphalt-to-aggregate ratio, density of asphalt, density of aggregates and air voids are known. The following equations can be defined.
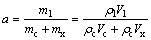 (7)
(7)
 (8)
(8)
where a is asphalt-to-aggregate ratio of designed asphalt mixture; ml, mc and mx are masses of asphalt, coarse aggregates and fine aggregates; ρl, ρc and ρx are densities of asphalt, coarse aggregates and fine aggregates; Vl, Vc and Vx are volumes of asphalt, coarse aggregates and fine aggregates; VV is the air void of designed asphalt mixture; and V is the total volume of a specific testing sample.
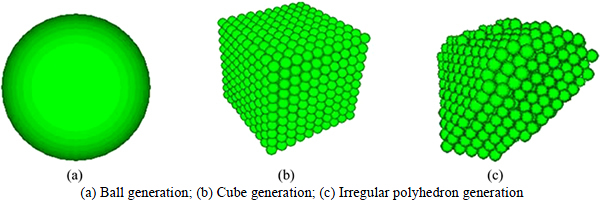
Fig. 4 Irregular aggregate particle generation:
Table 5 Randomly generated coarse aggregates with different sizes
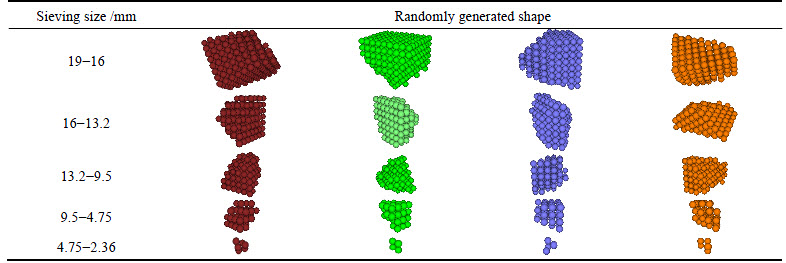

Fig. 5 Three kinds of real aggregates
2) Based on Eqs. (7) and (8), the total volume percent of aggregates in asphalt mixture can be calculated by Eq. (9). Meanwhile, according to the mass gradation of aggregates, the relationship between the volumes of coarse aggregates and fine aggregates is shown in Eq. (10).
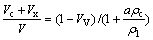 (9)
(9)
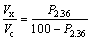 (10)
(10)
where P2.36 is the passing ratio on sieving size of 2.36 mm in the mass gradation of aggregates.
3) Equation (11) can be derived from Eqs. (9) and (10) to calculate the volume percent of coarse aggregates in asphalt mixture.
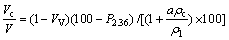 (11)
(11)
4) According to the mass gradation of aggregates, the volume percent of coarse aggregate on each sieving size can be calculated by Eq. (12).
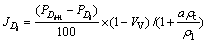 (12)
(12)
where Di are different sieving sizes for coarse aggregates, such as 2.36 mm, 4.75 mm and 9.5 mm; PDi is the passing ratio for sieving size Di; JDi is the volume percent of coarse aggregate on sieving size Di.
5) Finally, for a specific test sample, numbers of aggregates on each sieving size can be calculated based on Eq. (13).
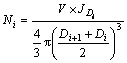 (13)
(13)
where Ni is the number of aggregates on sieving size of Di.
Based on the combination of the generating algorithm for single aggregate particle and the converting algorithm for volumetric gradation of aggregates, modeling procedure was built based on PFC3D to generate graded coarse aggregates. Figure 6 shows the basic generating steps for graded aggregates in the test sample of uniaxial creep test. Figure 7 shows the cross sections of virtual sample and actual samples for uniaxial creep test. It can be seen that the coarse aggregate skeleton of virtual sample is similar to that of actual test sample.
3.3 Modeling of asphalt mastic and air voids
Since asphalt mastic is considered a continuum medium filling into the voids of coarse aggregate skeleton, it can be modeled by using uniformly sized balls in PFC3D. As shown in Fig. 8(a), uniformly sized balls with small diameter (1 mm used in this work) were filled into the virtual space of test sample. After graded coarse aggregates were generated based on the previous modeling for aggregates, the small balls within aggregates were set as clumps to represent aggregates and the remaining balls outside aggregates were used to represent asphalt mastic. As shown in Fig. 8(b), a two- phase system composed of aggregates and asphalt mastic was generated. According to the target air void of designed asphalt mixture, as shown in Fig. 8(c), some of the small balls representing asphalt mastic were randomly deleted to represent the air voids in test sample. Finally, the virtual modeling of asphalt mixture was obtained.
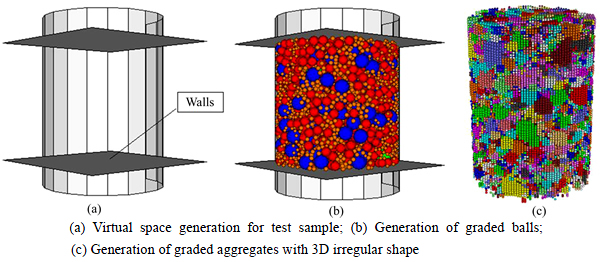
Fig. 6 Generation of graded coarse aggregates:

Fig. 7 Cross sections for virtual sample and actual sample:

Fig. 8 Virtual modeling of asphalt mixture:
3.4 Contact models and parameters
Since coarse aggregates were set as clumps, there are mainly three types of contacts within the virtual sample of asphalt mixture, which are contacts between aggregates, within asphalt mastic, and between aggregate and asphalt mastic. The contact-stiffness model and slipping model were set at contacts between aggregates while Burger’s models were set at contacts within asphalt mastic and between aggregate and asphalt mastic. Based on PFC3D manual and previous studies [22-26], the input parameters for different contacts are summarized in Tables 6, 7 and 8. In Table 6, kn, ks and μc are the normal stiffness, shear stiffness and friction coefficient at contacts between aggregates, respectively. In Table 7, Kmn, Cmn, Kkn and Ckn are the parameters of the Burger’s model at contacts within asphalt mastic at normal direction, respectively; and Kms, Cms, Kks and Cks are the parameters of the Burger’s model at contacts within mastic at shear direction, respectively. In Table 8, K′mn, C′mn, K′kn and C′kn are the parameters of the Burger’s model at contacts between aggregate and mastic at normal direction; K′ms, C′ms, K′ks and C′ks are the parameters of the Burger’s model at contacts between aggregate and mastic at shear direction, respectively.
Table 6 Input parameters at contacts between aggregates

Table 7 Input parameters at contacts within asphalt mastic

Table 8 Input parameters at contacts between aggregate and asphalt mastic

4 Virtual test
4.1 Virtual simulation of penetration test
Since aggregate skeleton has significant influence on the mechanical behavior of asphalt mixture. Virtual simulation of penetration test for coarse aggregates was conducted to verify the feasibility of the developed aggregate modeling. Based on the mass gradation in Table 2, the volume percent and numbers of coarse aggregates on each sieving size were determined as shown in Table 9. The virtual penetration test is demonstrated in Fig. 9. After graded coarse aggregates were generated as shown in Fig. 9(a), vibration and preloading procedures shown in Figs. 9 (b) and (c) were applied to getting compacted aggregate skeleton. After penetration load is applied as shown in Fig. 9(d), the penetration resistance along with penetration depth was collected every 50 calculating steps. The relationships between penetration depth and penetration resistance for both virtual test and actual test are shown in Fig. 10.
Table 9 Volume percent and numbers of aggregate on each sieving size for modeling
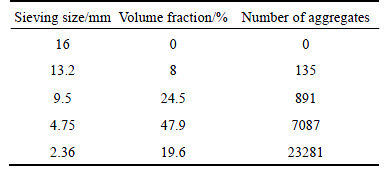
From Fig. 10, it can be seen that, due to the difference between virtual aggregates and actual aggregates, the curve from virtual test is not exactly the same with that from actual test. However, they are similar with each other. To conduct statistical analysis, five replicates were conducted in actual test while ten replicates were conducted in virtual test. The variability analysis of the final penetration resistance for actual test and virtual test are shown in the Fig. 11. It can be seen that, when the mean value of virtual test is similar to that of actual test, the standard deviation of virtual test is much smaller than that of actual test. It is indicated that the variation coefficient of virtual test is about 8% while the variation coefficient of actual test is about 15%. It proves the validity of the previous modeling algorithm and procedure for coarse aggregates.
4.2 Virtual simulation of uniaxial creep test
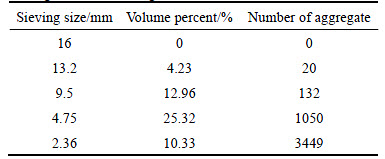
As listed in Table 10, to conduct virtual uniaxial creep test, the volumetric gradation of coarse aggregates and numbers of aggregate on each sieving size for uniaxial creep test sample were determined according to the previous proposed converting algorithm. Virtual uniaxial creep test was built and conducted by PFC3D. Figure 12 shows the sample and loading in virtual test.

Fig. 9 Virtul simulation of penetration test:
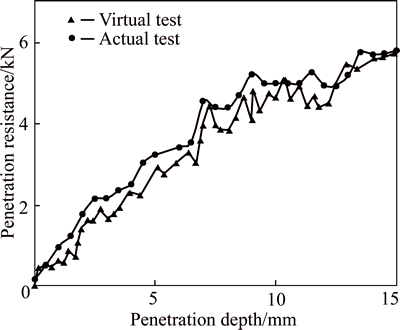
Fig. 10 Virtual test vs. actual test
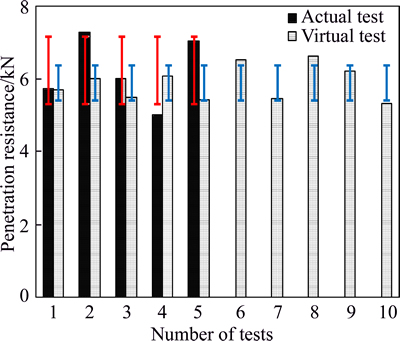
Fig. 11 Variability analysis of virtual test vs. actual test
Table 10 Volume percent and numbers of aggregate on each sieving size for modeling
The testing results of both virtual test and actual test are shown in Fig. 13. Due to the microstructure differences such as aggregate skeleton and air void distribution between virtual test and actual test, the testing result of virtual test is not exactly the same with actual test. However, the two testing curves have no obvious difference with each other. It proves the feasibility of the virtual modeling and simulation. As shown in Fig. 14, statistical analysis was conducted for both actual test and virtual test. The variation coefficient for virtual test is about 4% while the variation coefficient of actual test is about 10%. It is clearly indicated that virtual test has less variability than actual test.
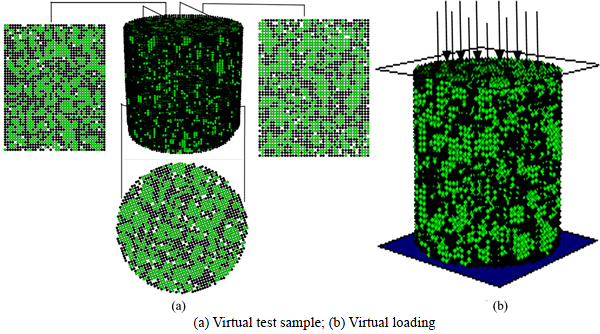
Fig. 12 Virtual uniaxial test:
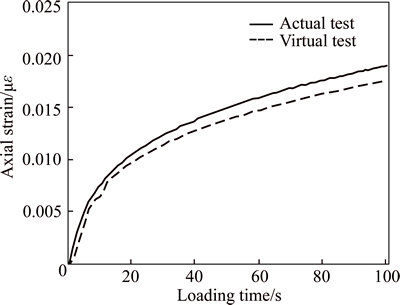
Fig. 13 Testing results of virtual test vs. actual test

Fig. 14 Variability analysis of virtual test vs. actual test
5 Conclusions
1) A randomly generating algorithm is proposed to characterize the three-dimensional irregular property of coarse aggregate. Based on the proposed algorithm for single aggregate particle, a modeling procedure is built to generate the graded aggregates in asphalt mixture. Finally, the microstructure of asphalt mixture is modeled by PFC3D.
2) Penetration test for coarse aggregates is designed and conducted in laboratory. Virtual test is built and conducted by PFC3D according to the laboratory test. It is proved that the developed modeling algorithm and procedure can characterize the property of aggregate particle and aggregate skeleton very well.
3) Virtual test for uniaxial creep test is built and conducted by PFC3D. It is indicated that the testing results of virtual test and laboratory test match each other well. Thus, the validity of microstructure modeling and virtual test for asphalt mixture built in this work is proved. Meanwhile, it proves that virtual test is easier to control and has much lower variability than laboratory test.
4) It is proved that virtual test based on PFC3D provides a promising way to investigate the micromechanical properties of asphalt mixture. However, there are still many problems related to PFC3D modeling to be solved for better microstructure characterization of asphalt mixture. Further studies should be focused on the characterization of surface texture and angularity of coarse aggregates, the irregular microstructure and distribution of air voids, and the computation efficiency of PFC3D.
References
[1] LIAO Gong-yun, YANG Yi-wen, HUANG Xiao-ming, XIANG Jin-yuan. Permanent deformation response parameters of asphalt mixtures for a new mix-confined repeated load test [J]. Journal of Central South University, 2013, 20(5): 1434-1442.
[2] QIAN Zhen-dong, HU Jing. Fracture properties of epoxy asphalt mixture based on extended finite element method [J]. Journal of Central South University, 2012, 19(11): 3335-3341.
[3] KIM Y R, BAEK C, UNDERWOOD B S, SUBRAMANIAN V, GUDDATI M N, LEE K. Application of viscoelastic continuum damage model based finite element analysis to predict the fatigue performance of asphalt pavements [J]. KSCE Journal of Civil Engineering, 2008, 12(2): 109-120.
[4] SADD M H, DAI Q L, PARAMESWARAN V, SHUKLA A. Simulation of asphalt materials using a finite element micromechanical model with damage mechanics [J]. Transportation Research Record: Journal of the Transportation Research Board, 2003, 1832: 86-95.
[5] KIM H, BUTTLAR G. Multi-scale fracture modeling of asphalt composite structures [J]. Composites Science and Technology, 2009, 69: 2716-2723.
[6] WANG Z, KWAN A, CHAN H. Mesoscopic study of concrete I: Generation of random aggregate structure and finite element mesh [J]. Computers & Structures, 1999, 70(5): 533-544.
[7] CHEN Jia-qi, ZHANG Miao,WANG Hao,LI Liang. Evaluation of thermal conductivity of asphalt concrete with heterogeneous microstructure [J]. Applied Thermal Engineering, 2015, 84: 368-374.
[8] SOUZA L T. Experimental testing and finite-element modeling to evaluate the effects of aggregate angularity on bituminous mixture performance [J]. Journal of Materials in Civil Engineering, 2007, 24(3): 249-258.
[9] CHEN Jia-qi, WANG Hao, LI Liang. Virtual testing of asphalt mixture with two-dimensional and three-dimensional random aggregate structures [J]. International Journal of Pavement Engineering, 2015, DOI: 10.1080/20298436.2015.1066005.
[10] CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies [J]. Géotechnique, 1979, 29(1): 47-65.
[11] CUNDALL P A. A discontinuous future for numerical modeling in geomechanics [J]. Proceedings of the Institution of Civil Engineers Geotechnical Engineering, 2001, 149(1): 41-47.
[12] ZHONG X, CHANG C S. Micromechanical modeling for behavior of cementitious granular materials [J]. Journal of Engineering Mechanics, 1999, 125(11): 1280-1285.
[13] BUTTLAR W G, YOU Z P. Discrete element modeling of asphalt concrete: A micro-fabric approach [J]. Transportation Research Record: Journal of the Transportation Research Board, 2001, 1757: 111-118.
[14] KIM H, BUTTLAR W G. Discrete fracture modeling of asphalt concrete [J]. International Journal of Solids and Structures, 2009, 46(13): 2593-2604.
[15] YOU Z, BUTTLAR W G. Micromechanical modeling approach to predict compressive dynamic moduli of asphalt mixture using the distinct element method [J]. Transportation Research Record, 2006, 1970: 73–83.
[16] CHEN J, PAN T, HUANG X M. Numerical investigation into the stiffness anisotropy of asphalt concrete from a microstructural perspective [J]. Construction and Building Materials, 2011, 25: 3059-3065.
[17] CHEN J, HUANG B, SHU X. Air-void distribution analysis of asphalt mixture using discrete element method [J]. Journal of Materials in Civil Engineering, 2013, 25(10): 1375-1385.
[18] YOU, Z, ADHIKARI S, DAI Q. Air void effect on an idealized asphalt mixture using two-dimensional and three-dimensional discrete element modeling approach [J]. International Journal of Pavement Engineering, 2010, 11(5): 381-391.
[19] JTG F40-2004. Technical specification for construction of highway asphalt pavement [S]. 2004.
[20] ALVAREZ A,MAHMOUD E,MARTIN A,MASAD E, ESTAKHRI C. Stone-on-stone contact of permeable friction course mixtures [J]. Journal of Materials in Civil Engineering,2010, 22(11): 1129-1138.
[21] JTG E20-2011. Standard test methods of bitumen and bituminous mixtures for highway engineering [S]. 2011. (in Chinese)
[22] Itasca Consulting Group. PFC3D manual Ver. 4.0 [M]. Minneapolis, 2008.
[23] LIU Y, DAI Q, YOU Z. Viscoelastic model for discrete element simulation of asphalt mixture [J]. Journal of Engineering Mechanics, 2009, 135(4): 324-333.
[24] YOU Z, ADHIKARI S, DAI Q. Three-dimensional discrete element models for asphalt mixtures [J]. Journal of Engineering Mechanics, 2008, 134(12): 1053-1062.
[25] HOU Shu-guang, ZHANG Dong, HUANG Xiao-ming. Investigation of the micro-mechanical response of asphalt mixtures by a three- dimensional discrete element model [J]. Journal of Wuhan University of Technology: Materials Science Edition, 2015, 30(2): 338-343.
[26] LIU Y, YOU Z. Visualization and simulation of asphalt concrete with randomly generated three-dimensional models [J]. Journal of Computing in Civil Engineering, 2009, 23(6): 340-347.
(Edited by YANG Hua)
Foundation item: Project(51378006) supported by National Natural Science Foundation of China; Project(141076) supported by Huoyingdong Foundation of the Ministry of Education of China; Project(2242015R30027) supported by Excellent Young Teacher Program of Southeast University, China: Project(BK20140109) supported by the Natural Science Foundation of Jiangsu Province, China
Received date: 2015-04-14; Accepted date: 2015-09-24
Corresponding author: MA Tao, PhD, Associate Professor; Tel: +86-25-83790551; E-mail: mataoseu@163.com
Abstract: The objective of this work is to model the microstructure of asphalt mixture and build virtual test for asphalt mixture by using Particle Flow Code in three dimensions (PFC3D) based on three-dimensional discrete element method. A randomly generating algorithm was proposed to capture the three-dimensional irregular shape of coarse aggregate. And then, modeling algorithm and method for graded aggregates were built. Based on the combination of modeling of coarse aggregates, asphalt mastic and air voids, three-dimensional virtual sample of asphalt mixture was modeled by using PFC3D. Virtual tests for penetration test of aggregate and uniaxial creep test of asphalt mixture were built and conducted by using PFC3D. By comparison of the testing results between virtual tests and actual laboratory tests, the validity of the microstructure modeling and virtual test built in this study was verified. Additionally, compared with laboratory test, the virtual test is easier to conduct and has less variability. It is proved that microstructure modeling and virtual test based on three-dimensional discrete element method is a promising way to conduct research of asphalt mixture.


