J. Cent. South Univ. (2016) 23: 3171-3182
DOI: 10.1007/s11771-016-3383-7
Monte-Carlo based cascade control approach with focus on real overactuated space systems
M. Shahi1, A.H. Mazinan2
1. Department of Electrical Engineering, Birjand Branch, Islamic Azad University (IAU), Birjand, Iran;
2. Department of Control Engineering, Faculty of Electrical Engineering, South Tehran Branch,
Islamic Azad University (IAU), No. 209, North Iranshahr St., P.O. Box 11365/4435, Tehran, Iran
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract:
The present research relies on a cascade control approach through the Monte-Carlo based method in the presence of uncertainties to evaluate the performance of the real overactuated space systems. A number of potential investigations in this area are first considered to prepare an idea with respect to state-of-the-art. The insight proposed here is organized to present attitude cascade control approach including the low thrust in connection with the high thrust to be implemented, while the aforementioned Monte-Carlo based method is carried out to guarantee the approach performance. It is noted that the investigated outcomes are efficient to handle a class of space systems presented via the center of mass and the moments of inertial. And also a number of profiles for the thrust vector and the misalignments as the disturbances all vary in its span of nominal variations. The acquired results are finally analyzed in line with some well-known benchmarks to verify the approach efficiency. The key core of finding in the research is to propose a novel 3-axis control approach to deal with all the mentioned uncertainties of space systems under control, in a synchronous manner, as long as the appropriate models in the low-high thrusts are realized.
Key words:
1 Introduction
With the development of space systems technologies, an efficient control approach to be able to deal with space systems may be valuable, due to the fact that the potential outcomes in this filed are a challenging issue. In a word, the present research attempts to address the new insight to cope with a class of overactuated space systems in the presence of uncertainties, while the appropriate models in the low- high thrusts could be analyzed to guarantee the system performance, accurately. It is noted that the approach investigated here can deal with the aforementioned systems to be controlled, as long as the same parameters are varied in a wide range of nominal variations, in an abrupt manner, with respect to time. The present approach is designed through Monte-Carlo based method to be applicable in two modes of propellant engine including on and off that are correspondingly related to space systems maneuvers through three control channels to evaluate the same system performance. These channels are uniquely listed in the present research as the low thrust engine off mode control and the low-high thrust engine on mode control respectively. The engine on mode is related to orbital maneuvers, in finite burn time, while the corresponding engine off mode is related to thermal, communication, attitude maneuvers and so on, in non-finite burn, respectively. The strategy is developed in four loops, as long as two of them are related to high-low thrust 3-axis control, in engine on mode, and the rest of them are related to low thrust 3-axis control, in engine off mode, as well. The best outcomes regarding the approach analysis are finally presented. It can be shown that a number of on-off thrusters are here employed to handle the present loops, as long as a set of the pulse-width pulse-frequencies (PWPFs) and the control allocations (CAs) are correspondingly realized to guarantee the system performance.
Now, in order to consider the contribution of the approach presented, the background of the same topics during the past decade in this area is now focused. XIAO et al [1] presented attitude tracking control of rigid spacecraft under actuator misalignment and fault, where the control approach asymptotically stabilizes the closed- loop attitude tracking system and also the desired attitude trajectories can be tracked in finite time. ZOU et al [2] reveald attitude coordination control regarding the group of spacecraft without velocity measurements. Hereinafter, SABATINI et al [3] proposed a method for delay compensation in the area of attitude control of flexible spacecraft, while ZHENG and SONG [4] suggested an autonomous attitude coordinated control for a spacecraft.
YANG et al [5] proposed nonlinear attitude tracking control for spacecraft. They tried to deal with the attitude tracking control for spacecraft formation with communication delays. HUO et al [6] suggested finite-time fault tolerant attitude stabilization control for rigid spacecraft. A sliding mode control scheme was proposed to solve the problem of attitude stabilization for a rigid spacecraft [6]. In the research by DU and LI [7], an attitude synchronization control for a class of flexible spacecraft was proposed to deal with the problem of attitude synchronization for a class of flexible spacecraft. SONG et al [8] realized finite-time control for nonlinear spacecraft attitude via terminal sliding mode strategy. In their research, a terminal sliding mode control strategy with double closed loops was suggested to deal with spacecraft attitude control problem. LU and XIA [9] dealt with an adaptive attitude tracking control for rigid spacecraft with finite-time convergence. In this research work, the attitude tracking control problem was addressed for rigid spacecraft with external disturbances and inertia uncertainties. YANG [10] reviewed spacecraft attitude determination and control using quaternion based PDLQR method. In this review, the present quaternion based methods were discussed for the spacecraft attitude determination, while the corresponding control was considered.
An adaptive fuzzy fault-tolerant attitude control of spacecraft was presented [11]. The attitude control of was investigated spacecraft, since unknown mass moment of inertia matrix, external disturbances, actuator failures and input constraints were all existed [11]. Robust attitude control for spacecraft under assigned velocity and control constraints was realizd [12], while the leader-following attitude control of multiple rigid spacecraft systems was dealt [13]. Hereinafter, the work was presented in the area of attitude dynamics and control of miniature spacecraft via pseudo-wheels [14], the research was given in attitude control of rigid spacecraft with disturbance generated by time varying exo-systems [15]. Robust decentralized attitude coordination control of spacecraft formation was proposed [16], while robust fault-tolerant tracking control design for spacecraft under control input saturation was proposed in Ref. [17]. A design of control strategy for rigid spacecraft attitude tracking with actuator saturation was proposed [18], and an optimal sliding mode controllers for attitude tracking of spacecraft via Lyapunov function was suggested [19]. Afterwards, time-varying sliding mode controls in the area of rigid spacecraft attitude tracking is presented by JIN et al [20], while adaptive sliding mode control with its application to six-DOF relative motion of spacecraft under input constraint was given by WU et al [21]. Furthermore, adaptive backstepping fault-tolerant control for flexible spacecraft under unknown bounded disturbances as well as actuator failures was presented by JIANG et al [22] and realization of attitude control of spacecraft was presented by BUTYRIN et al [23], as long as research in relative position finite-time coordinated tracking control of spacecraft formation without velocity measurements by HU and ZHANG [24]. Regarding the control allocation research, a survey was presented JOHANSEN and FOSSEN [25] to address this issue. With this purpose, the subject of control allocation suggested the advantage of a modular design, as long as the high-level motion control algorithm was designed, since there were no detailed knowledge about the effectors and actuators. ZACCARIAN [26] proposed dynamic allocation for input redundant control systems. It was proposed to address control systems under redundant actuators.
Research by SERVIDIA [27] was to deal with control allocation for gimbaled/fixed thrusters. There were some overactuated control systems, which used a control distribution law between the controller and the actuators. YEH [28] presented an strategy to sliding-mode adaptive attitude controller design with its application to spacecrafts with thrusters, while JIN et al [29] suggested time-varying sliding mode attitude tracking control strategy in rigid spacecraft [28-29]. The key core of finding the new outcomes in the approach presented here is to realize a unique three-channel comprehensive control strategy that is able to deal with a class of the space systems under control with efficient results that enable variations of a set of parameters with high accuracy with respect to the potential investigations in this area, as long as the appropriate high and low thruster’s dynamics are investigated through a Monte- Carlo based method.
The rest of the manuscript is organized as follows. The proposed control approach including preliminary materials and the overall strategy realization are first presented in Section 2, while the simulation results and concluding remarks are then presented in Sections 3 and 4, respectively.
2 Proposed control approach
2.1 Preliminary materials
2.1.1 A brief discussion of space system dynamics
The attitude dynamic equation is organized based on the following formula:
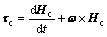(1)
where τc denotes 3-axis control torques; Hc denotes angular momentum vector in the body coordinate that contains Hμ and finally ω denotes as angular velocity vector in the body coordinate that contains ωμ, where μ=x, y, z. Now, by addressing the 3-axis angular velocities, the 3-axis control torques of the spacecraft are realized as
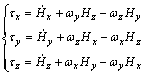(2)
Moreover, the attitude dynamic equations are easily resulted by
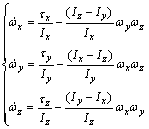(3)
Now, the space model can be represented through the attitude kinematic and the dynamics equations. Regarding the first equation, it is common to represent using various attitude parameters such as Rodrigues, Euler angles, quaternion vector and others, but the representation via quaternion vector is more applicable. All in all, this representation is taken into consideration, as an appropriate candidate, to present the attitude behavior of the spacecraft. With this purpose, the qs can first be presented in four dimensional space as follows:
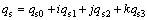(4)
where qsi; i=0, 1, 2, 3 has one real and three imaginary elements and also the conditions ||qs||=1 must be satisfied. Now, the relations between ωx, ωy, ωz and the qsi can be presented by
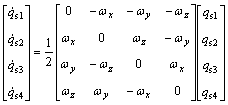(5)
And the relations between f, θ, ψ and the qsi are now also given by
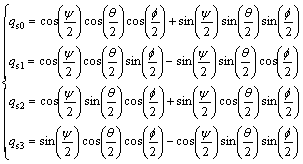(6)
where the Euler angles can easily be calculated as
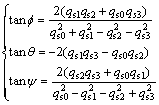(7)
2.1.2 PWPF realization
The PWPF is used in so many environments such as space systems, as shown in Fig. 1.
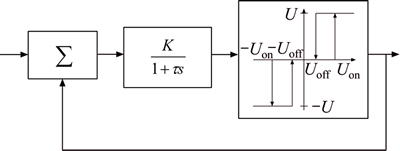
Fig. 1 Schematic diagram of PWPF
The static characteristics parameters of the PWPF are briefly tabulated in Table 1.
2.1.3 CA realization
The realization of the control allocation is to command on distribution logic as an algorithm whose function is to select specific thrusters and calculate their firing durations to realize force and torque commands, which are derived from the control of the spacecraft. This scheme is briefly given as
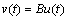(8)
where u(t) is taken as the real control and v(t) is also taken as its virtual control, while B is taken as a constant matrix. The advantage of the control allocation is to deal with a number of actuators separately and efficiently. In general, to realize an allocation scheme, a pseudo inverse matrix needs to be calculated. The torques in three axes including τx, τy and τz and the corresponding thruster’s levels including δi (i=1, 2, …, n) are presented by the following:
Table 1 Static parameters of PWPF modulator and its formula
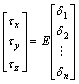(9)
It can be shown that there is a total of the eight thrusters, where the four high thrusters (Th,yzi; i=1, 2, 3, 4) are used to deal with the spacecraft in the y and z axes in high thrust mode and also the four further low thrusters Tl,xi; (i=1, 2, 3, 4) are used to deal with the spacecraft in the x axis in low thrust mode as presented in the proposed approach by 4Tl,x and 4Th,yz. It is emphasized that the thruster’s dynamics is given in the form of the first order plus time delay by
(10)
where τ and td are traditionally taken as the system time constant and the delay. The El,x and Eh,yz thruster’s configuration (TG) matrices in low and high thrust modes are taken as
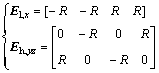(11)
where R is taken as the thruster’s arm. Based upon the information presented, the modules of the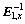 
and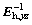 
are taken as the corresponding inverse matrices to be organized. Correspondingly, the 3-axis control torques in both low and high thrust modes are calculated as
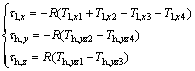(12)
Due to the fact that δi (i=1, 2, …, n) in Eq. (9) is taken as a sequence of 0 and T, three-axis relay including Rl,x and Rh,yz needs to be realized through fon/off as its relay functions. In such case, the generation of binary information for the whole of on-off thrusters is truly guaranteed, although the parameters τl,x, τh,y and τh,z may be changed to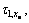 
and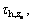 
namely, the efficient torques. The relation of the high-low torques in the three axes and its efficient ones are presented by
(13)
It is needed to note that the information presented here is only related to engine on mode control and the outcomes regarding the engine off mode control can easily be documented in the same way.
2.2 Overall approach realization
The realization of the overall approach is presented along with the integrations of a number of modules to deal with a class of space systems, as illustrated in Fig. 2. It means that the specification of a chosen class in a space system is related to the moments of inertia, the center of mass concerning the overall space system and also the profiles of the thrust vector, the arm and misalignments concerning the propellant engine of the same space system. Now, to follow the investigated outcomes, at first, the specific mode of propellant engine has to be identified through engine on mode entitled EOM in the conditional block. As apparent, each one of the modes needs to be dealt with in the three axes. With this purpose, there are three channels including the low thrust 3-axis engine off mode control, the low thrust x-axis engine on mode control and finally high thrust y, z-axis engine on mode control, respectively. It is obvious that the procedures of realizing them are different, due to the fact that their applicability is not the same.
Regarding the 3-axis engine off mode control, as unified in the module of the low thrust inner-outer loop control approach, it is organized based upon the concept of quaternion. In this case, the variation of the 3-axis referenced commands may be larger than the corresponding 3-axis engine on mode control and therefore the Euler angles processing may be encountered some singularities. It is recommended to use the quaternion vector as an appropriate choice, in the same way, to cover large angles space maneuvers. Moreover, the responsibility of the engine off mode control is usually known in the absence of the propellant engine thrust vector and the corresponding propellant misalignments as disturbances that can truly be ignored. It aims to deal with the proposed approach in its low thrust in one such case. In this control mode, the time limitation of orbital maneuvers is not considered and the non-burning time can be usually chosen larger than finite time burning time.
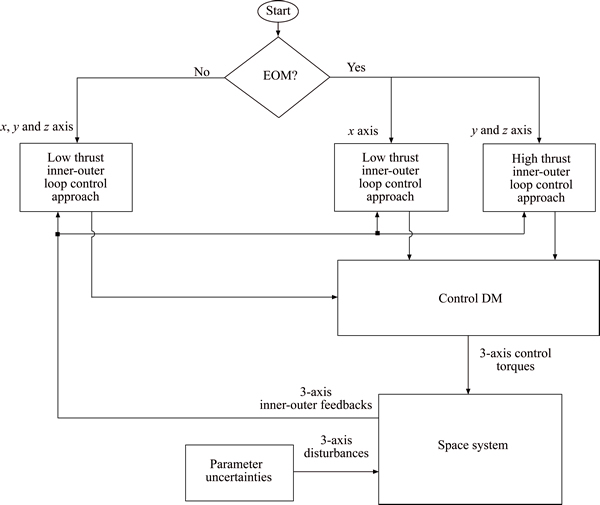
Fig. 2 Proposed control approach
Regarding the 3-axis engine on mode control, as unified in the modules of the low and the high thrusts inner-outer loop control approaches, the propellant engine thrust vector and the corresponding propellant misalignments as disturbances cannot truly be ignored and therefore the proposed 3-axis channel in the same case needs to be designed, in its low-high thrusts, to handle the 3-axis disturbances torques, in finite burning time. It is certainly possible to organize the whole of x, y and z axes in the high thrust in the present engine on mode, although the tracking of the x-axis of the space system via the approach proposed here plays insignificant role to guarantee the system performance with respect to the tracking of both y and z referenced commands. It is easy to note that the performance of the space system may be appropriate without x-axis referenced commands control. In fact, the x-axis control plays a key role to present a decoupling space system that is suitable to handle with respect to its coupling ones. Therefore, in order to present an efficient approach to be applicable in real environments, the x-axis referenced command is dealt with in its low thrust. Moreover, it is noted that a significant amount of time does not allow us to handle an appropriate orbital maneuvers and therefore the time consumed in the present engine mode control is always limited as finite time burning time. Subsequently, in this engine mode control, the outcomes may be useful to deal with small angle maneuvers such as orbital ones. And it is also noted that the Euler angle processing is known as an appropriate solution to track referenced commands in the process of carrying out the orbital maneuvers.
Now, it is the right time to initialize a number of parameters, where in engine on mode they are listed as the initial attitude of system, the burning time, the levels of low-high thrusters, the span of the moments of inertia, the span of the engine arms, the thruster dynamics, the 3-axis control coefficients, the PWPF modulator, the CA and finally the sample time of control loops. Correspondingly, in engine off mode, they are listed as above-referenced items, expect the low thrust is focused and also the parameters variations are limited. Moreover, in the same way, the non-burning time that can be larger or smaller than the corresponding burning time is consumed. The proposed strategy is developed to track the guidance referenced commands. Due to the fact that the variations of the present referenced commands are limited with respect to time, in engine on mode, the procedure is realized along with the Euler angles. In the same way, the present procedure is realized along with the quaternion vector, in engine off mode, because of the fact that the variations of the present referenced commands may be extended with respect to time. Based upon the matter presented here, in engine off mode, the referenced commands have to be translated to its quaternion vector information to calculate the quaternion vector errors for the purpose of handling the outer loop PD control approach by the following
(14)
where by using qe=qrefqs, its expanded form can be written by
(15)
In one such case, the thrust’s level T is the same for all the thrusters and also the conditions ||qref||=1 should be satisfied. In this formulation, qe is taken as quaternion error and qs is taken as system quaternion and finally qrefis taken as referenced quaternion. The inner loop P control approach is now realized to deal with the 3-axis angular rates to generate the appropriate commands for the four low thrust on-off thrusters, while PWPF, as tabulated Table 1, pseudo inverse for TG, low thrust CA are all employed. Now, by using TG matrix, the 3-axis low thrust torques control, in engine off mode, can be generated. The procedure considered here is correspondingly repeated, in engine on mode, expect the x and y-z axes are separated, while the x-axis is related to the other specific low thrust and y-z axes are related to high thrust. Moreover, this is organized based upon Euler angles processing and also the outer loops are dealt with via PID control approach. Subsequently, the 3-axis torques control in engine on mode are produced. The information in both modes of propellant engine is used to provide the control decision making (DM), which is realized to deal with the control torques in the present modes. It means that the DM is only acting as a soft switch between the output of the engine on and off mode control strategy and the space system to choose one of them at each instant of time. The 3-axis disturbances are also provided by focusing on the profiles of the thrust vector (F), engine misalignments (φmis, θmis, ψmis), and engine arm (r) to be varied by the variation of the center of mass (Δcg), as input sources. It is apparent that the present 3-axis disturbances are omitted provided that the present sources are ignored. The idea of generating the present disturbances is inspired of the following:
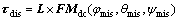(16)
The outcomes are finalized, while the matrix multiplication (MMP) of the discrete cosine matrix (DCM, Mdc) of the misalignments profile can be multiplied in cross form by L=r+Δcg deviation profile, where L is the moment of inertia at each instant of time.
3 Simulation results
At first, Monte-Carlo based method is carried out to find the dynamics of the high and low thrusters. After that, two experiments regarding the engine on and off modes control are realized. In the case of high thrusters, four of them including 300 N, 400 N, 500 N and finally 600 N is initialized, while the thruster’s rise time is taken as 23 ms, 46 ms, 69 ms and 69 ms. Moreover, in the case of low thrusters, four of them including 25 N, 50 N, 100 N and finally 150 N are initialized, while the thruster’s rise time is taken as 23 ms. It should be noted that uncertainties are considered for three parameters of the system under control including the engine misalignments, the center of mass and thrust vector in the span of 90%-120%. It means that the main profiles of these parameters are updated as φmisu, θmisu, ψmisu, Fu and Δcgu through uncertainties by multiplying to KEm, Kcg, KFt, respectively, which are randomly taken along with Monte-Carlo based method between 0.9 and 1.2.
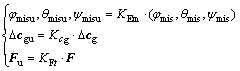(17)
Now, the moments of inertia is initially taken as
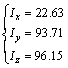(18)
And the 3-axis engine arm is initially taken as r=[-0.1, 0, 0]T. In one such case, the initial parameters, in engine off mode, are tabulated in Table 2. It is needed to note that the coefficients of the control approach and also the PWPF, in the present tables, are all carefully tuned via MATLAB known optimization toolbox.
Table 2 Initial parameters of proposed control strategy in engine off mode (Experiment #1)
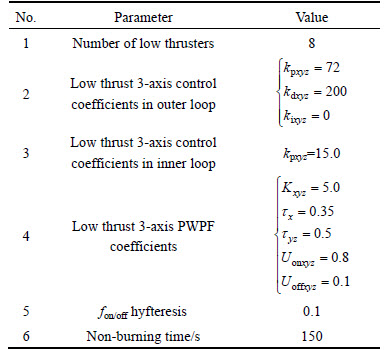
Moreover, the initial parameters, in engine on mode, are tabulated in Table 3. The outcomes regarding Eq. (17) are also illustrated in Figs. 3-5, respectively.
Now, by initializing the thruster’s rise time to be 69, 46 and 23 ms, the high and low thruster’s candidates to guarantee the approach performance in the presence of the lower and upper band of the uncertainties that are now focused on 90% and 120% are all tabulated in Table 4. The results of 3-axis steady state errors in the rise time of 69, 46 and 23 ms regarding Table 4 are correspondingly illustrated in Figs. 6-8, respectively.
Now, it is the right time to realize two experiments, while the results, tabulated in Table 4, can be taken in its worst case, i.e.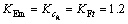 
to finalize the outcomes presented via Monte-Carlo based method. In fact, by initializing the high and low thruster’s dynamics, the present two experiments including engine off mode (Experiment #1) and engine on mode (Experiment #2) are now organized to be considered. Regarding the Experiment #1, the 3-axis referenced commands tracking are illustrated in Figs. 9-11, respectively, while the related referenced commands tracking errors are correspondingly illustrated in Fig. 12.
The quaternion referenced commands tracking in the present experiment versus the information presented in Figs. 9-11 are illustrated in Figs. 13(a)-(d),respectively.
Table 3 Initial parameters of proposed control strategy in engine on mode (Experiment #2)
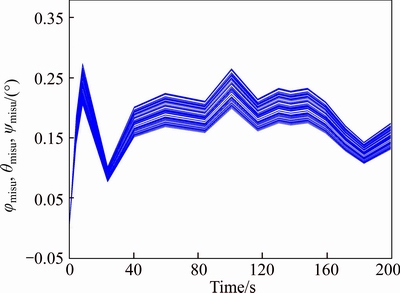
Fig. 3 Profile of φmisu, θmisu, ψmisu in the presence of band of uncertainties
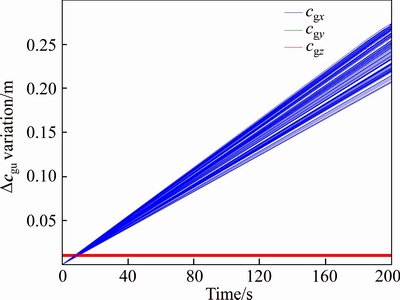
Fig. 4 Profile of Δcgu in the presence of band of uncertainties
Fig. 5 Profile of Fu in the presence of band of uncertainties
Table 4 High and low thruster’s dynamics to guarantee system performance in presence of lower and upper band of uncertainties
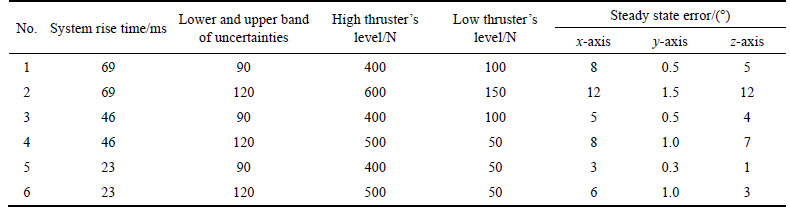
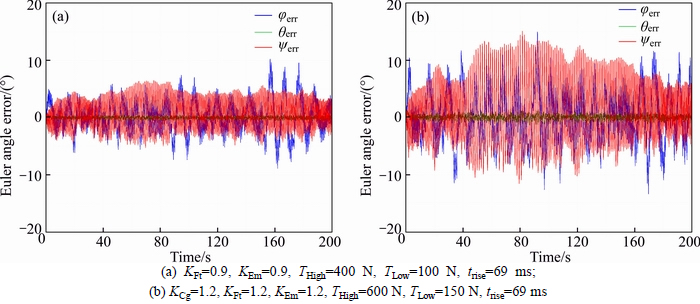
Fig. 6 3-axis steady state errors regarding rise time of 69 ms:
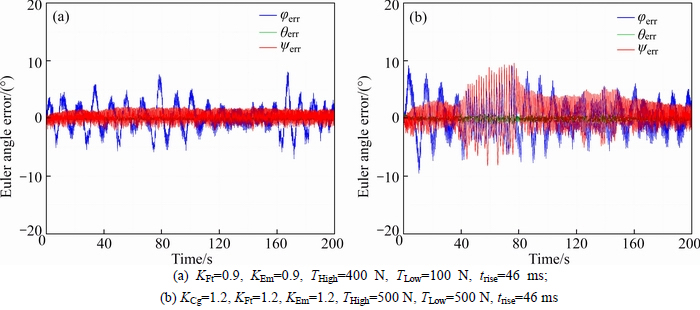
Fig. 7 3-axis steady state errors regarding rise time of 46 ms:
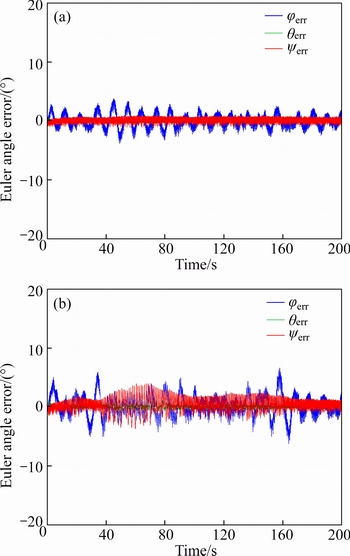
Fig. 8 3-axis steady state errors regarding rise time of 23 ms
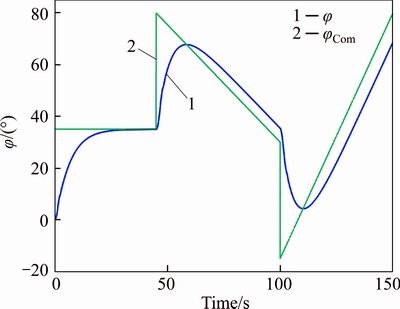
Fig. 9 x-axis referenced command tracking of Experiment #1
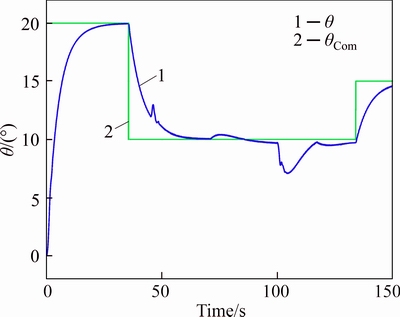
Fig. 10 y-axis referenced command tracking of Experiment #1
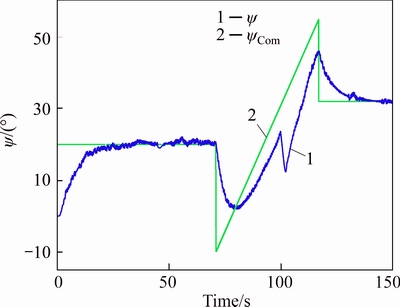
Fig. 11 z-axis referenced command tracking of Experiment #1
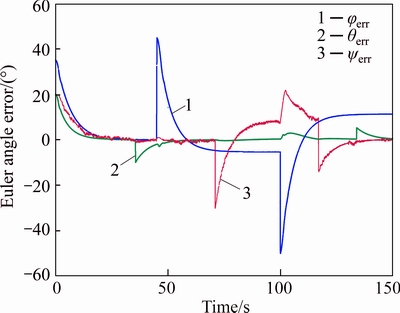
Fig. 12 3-axis referenced commands tracking errors of Experiment #1
Regarding Experiment #2, at first, the 3-axis moments of inertial and 3-axis L are illustrated in Figs. 14-15, respectively.
The tracking outcomes of the referenced commands are presented in Figs. 16-18, respectively. Correspondingly, the 3-axis referenced commands tracking errors are all presented in Fig. 19.
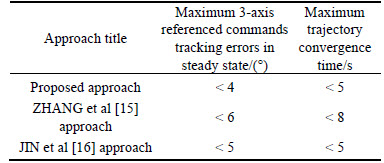
Hereinafter, in an effort to make the investigated results in the comparable manner, the two potential benchmarks including the Zhang’s [15] and the JIN’s [16] approaches are now chosen to analyze. Moreover, there are the following criteria considered in Table 5 including 1) the maximum 3-axis referenced commands tracking errors in steady state and 2) the trajectory convergence time, which are all important to evaluate the proposed approach performances with respect to the corresponding benchmarks. As a deduction matter, the results indicate that the proposed control approach is now well behaved in line with the present benchmarks regarding item 1), while the proposed control approach as well as the Erdong approach is also well behaved regarding item 2), with respect to the rest aforementioned approach.
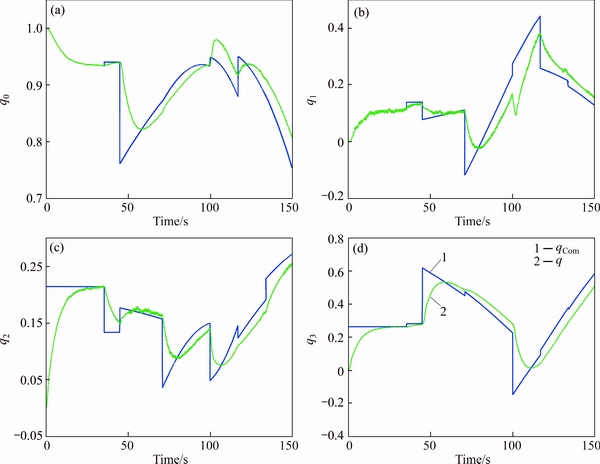
Fig. 13 Quaternion referenced commands tracking of Experiment #1
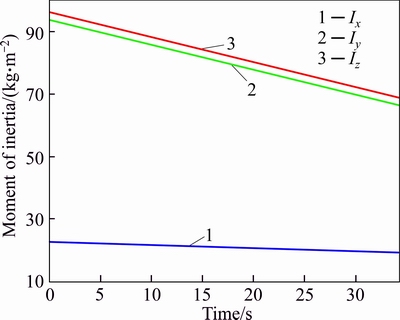
Fig. 14 Moments of inertial of space system of Experiment #2
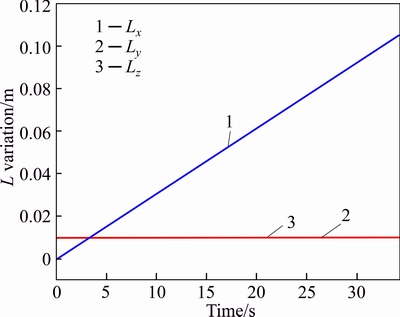
Fig. 15 3-axis L variation of Experiment #2
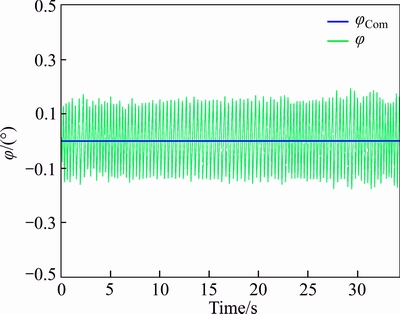
Fig. 16 x-axis referenced command tracking of Experiment #2
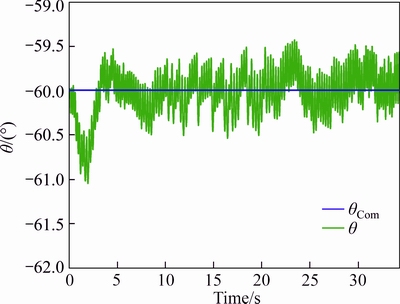
Fig. 17 y-axis referenced command tracking of Experiment #2
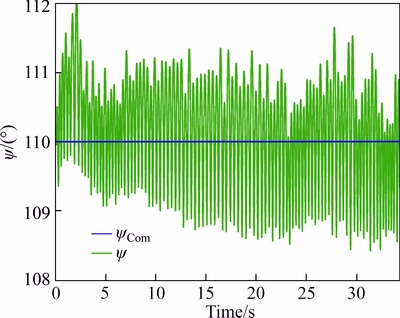
Fig. 18 z-axis referenced command tracking of Experiment #2
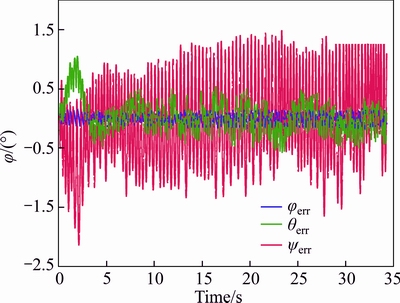
Fig. 19 3-axis referenced commands tracking errors of Experiment #2
Table 5 Verification of proposed control approach with respect to corresponding benchmarks
4 Conclusions
There is a need to develop the space systems technologies with respect to state-of-the-art, due to the fact that these outcomes can play a significant role in both real and academic environments. With a focus on new strategies to cope with a class of space systems, the proposed control approach is organized to implement on a wide range of space parameter uncertainties, while the processes of employing the low and the high thrusts are investigated through the Monte-Carlo based method. In this way, the present control method is designed applicable in two modes of propellant engine including on and off, which are related to a number of maneuvers. In a word, the low thrust control in connection with the low-high thrusts control is dealt with via the research, in a synchronous manner. Based upon the results presented here, the proposed strategy is realized in four loops that are working, synchronously. It is noted that two of them are related to high-low thrusts control in engine on mode, while the rest of them are also related to low thrust control in engine off mode, respectively. A set of the pulse-width pulse-frequencies are used in the approach proposed here in association with the control allocations to deal with a number of on-off reaction thrusters to guarantee the appropriate referenced commands tracking in both modes of the aforementioned propellant engine.
References
[1] XIAO Bing, HU Qing-lei, WANG Dan-wei, POH E K. Attitude tracking control of rigid spacecraft with actuator misalignment and fault [J]. IEEE Transactions on Control Systems Technology, 2013, 21(6): 2360-2366.
[2] ZOU An-min, KUMAR K D, HOU Zeng-guang. Attitude coordination control for a group of spacecraft without velocity measurements [J]. IEEE Transactions on Control Systems Technology, 2012, 20(5): 1160-1174.
[3] SABATINI M, GASBARRI P, PALMERINI G B. Delay compensation for controlling flexible space multibodies: Dynamic modeling and experiments [J]. Control Engineering Practice, 2015, 45: 147-162.
[4] ZHENG Zhong, SONG Shen-min. Autonomous attitude coordinated control for spacecraft formation with input constraint, model uncertainties, and external disturbances [J]. Chinese Journal of Aeronautics, 2014, 27(3): 602-612.
[5] YANG Hong-jiu, YOU Xiu, XIA Yuan-qing, LIU Zhi-xin. Nonlinear attitude tracking control for spacecraft formation with multiple delays [J]. Advances in Space Research, 2014, 54(4): 759-769.
[6] HUO Xing, HU Qing-lei, XIAO Bing. Finite-time fault tolerant attitude stabilization control for rigid spacecraft [J]. ISA Transactions, 2014, 53(2): 241-250.
[7] DU Hai-bo, LI Shi-hua. Attitude synchronization control for a group of flexible spacecraft [J]. Automatica, 2014, 50(2): 646-651.
[8] SONG Zhan-kui, LI Hong-xing, SUN Kai-biao. Finite-time control for nonlinear spacecraft attitude based on terminal sliding mode technique [J]. ISA Transactions, 2014, 53(1): 117-124.
[9] LU Kun-feng, XIA Yuan-qing. Adaptive attitude tracking control for rigid spacecraft with finite-time convergence [J]. Automatica, 2013, 49(12): 3591-3599.
[10] YANG Y. Spacecraft attitude determination and control: Quaternion based PDLQR method [J]. Annual Reviews in Control, 2012, 36(2): 198-219.
[11] ZOU An-min, KUMAR K D. Adaptive fuzzy fault-tolerant attitude control of spacecraft [J]. Control Engineering Practice, 2011, 19(1): 10-21.
[12] HU Qing-lei, LI Bo, ZHANG You-min. Robust attitude control design for spacecraft under assigned velocity and control constraints [J]. ISA Transactions, 2013, 52(4): 480-493.
[13] CAI He, HUANG Jie. The leader-following attitude control of multiple rigid spacecraft systems [J]. Automatica, 2014, 50(4): 1109-1115.
[14] KUO Yong-lin, WU Tsung-liang. Open-loop and closed-loop attitude dynamics and controls of miniature spacecraft using pseudo wheels [J]. Computers & Mathematics with Applications, 2012. 64(5): 1282-1290.
[15] ZHANG Xu-xi, LIU Xian-ping, ZHU Qi-dan. Attitude control of rigid spacecraft with disturbance generated by time varying exosystems [J]. Communications in Nonlinear Science and Numerical Simulation, 2014, 19(7): 2423-2434.
[16] JIN Er-dong, JIANG Xiao-lei, SUN Zhao-wei. Robust decentralized attitude coordination control of spacecraft formation [J]. Systems & Control Letters, 2008, 57(7): 567-577.
[17] BUSTAN D, PARIZ N, SANI S K H. Robust fault-tolerant tracking control design for spacecraft under control input saturation [J]. ISA Transactions, 2014, 53(4): 1073-1080.
[18] LU Kun-feng, XIA Yuan-qing, FU Meng-yin. Controller design for rigid spacecraft attitude tracking with actuator saturation [J]. Information Sciences, 2013, 220(20): 343-366.
[19] PUKDEBOON C, ZINOBER A S I. Control Lyapunov function optimal sliding mode controllers for attitude tracking of spacecraft [J]. Journal of the Franklin Institute, 2012, 349(2): 456-475.
[20] JIN Yong-qiang, LIU Xiang-dong, QIU Wei, HOU Chao-zhen. Time-varying sliding mode controls in rigid spacecraft attitude tracking [J]. Chinese Journal of Aeronautics, 2008, 21(4): 352-360.
[21] WU Jin-jie, LIU Kun, HAN Da-peng. Adaptive sliding mode control for six-DOF relative motion of spacecraft with input constraint [J]. Acta Astronautica, 2013, 87: 64-76.
[22] JIANG Ye, HU Qing-lei, MA Guang-fu. Adaptive backstepping fault-tolerant control for flexible spacecraft with unknown bounded disturbances and actuator failures [J]. ISA Transactions, 2010, 49(1): 57-69.
[23] BUTYRIN S A, MAKAROV V P, MUKUMOV R R, SOMOV Y E, VASSILYEV S N. An expert system for design of spacecraft attitude control systems [J]. Artificial Intelligence in Engineering, 1997, 11(1): 49-59.
[24] HU Qing-lei, ZHANG Jian. Relative position finite-time coordinated tracking control of spacecraft formation without velocity measurements [J]. ISA Transactions, 2015, 54: 60-74.
[25] JOHANSEN T A, FOSSEN T I. Control allocation—A survey [J]. Automatica, 2013, 49(5): 1087-1103.
[26] ZACCARIAN L. Dynamic allocation for input redundant control systems [J]. Automatica, 2009, 45(6): 1431-1438.
[27] SERVIDIA A A. Control allocation for gimballed/fixed thrusters [J]. Acta Astronautica, 2010, 66(3/4): 587-594.
[28] YEH F K. Sliding-mode adaptive attitude controller design for spacecrafts with thrusters [J]. IET Control Theory and Applications, 2010, 4(7): 1254-1264.
[29] JIN Yong-qiang, LIU Xiang-dong, QIU Wei, HOU Chao-zhen. Time-varying sliding mode controls in rigid spacecraft attitude tracking [J]. Chinese Journal of Aeronautics, 2008, 21(4): 352-360.
(Edited by FANG Jing-hua)
Received date: 2015-09-28; Accepted date: 2016-01-27
Corresponding author: M. Shahi, Assistant Professor; E-mail: m.shahi@iaubir.ac.ir
Abstract: The present research relies on a cascade control approach through the Monte-Carlo based method in the presence of uncertainties to evaluate the performance of the real overactuated space systems. A number of potential investigations in this area are first considered to prepare an idea with respect to state-of-the-art. The insight proposed here is organized to present attitude cascade control approach including the low thrust in connection with the high thrust to be implemented, while the aforementioned Monte-Carlo based method is carried out to guarantee the approach performance. It is noted that the investigated outcomes are efficient to handle a class of space systems presented via the center of mass and the moments of inertial. And also a number of profiles for the thrust vector and the misalignments as the disturbances all vary in its span of nominal variations. The acquired results are finally analyzed in line with some well-known benchmarks to verify the approach efficiency. The key core of finding in the research is to propose a novel 3-axis control approach to deal with all the mentioned uncertainties of space systems under control, in a synchronous manner, as long as the appropriate models in the low-high thrusts are realized.
