J. Cent. South Univ. Technol. (2008) 15: 159-164

DOI: 10.1007/s11771-008-0031-x

Influence of crystallographic orientation on growth behavior of spherical voids

ZHANG Xin-ming(张新明)¹, LIU Wen-hui(刘文辉)^{1, 2}, TANG Jian-guo(唐建国)¹, YE Ling-ying(叶凌英)¹

(1. School of Materials Science and Engineering, Central South University, Changsha 410083, China;

2. College of Electromechanical Engineering, Hunan University of Science and Technology,

Xiangtan 411201, China)

Key words:

crystallographic orientation; void growth; crystal plasticity; user subroutine; finite element method；

1 Introduction

Ductile fracture that occurs through the nucleation, growth and coalescence of voids, is a primary mode of material failure. It is important to predict the condition of void growth and coalescence when material is subjected to large plastic deformation. Many researchers applied a constitutive model, such as the GURSON model to simulate void growth and coalescence^[1-6]. All these researches assumed that the material possesses isotropic constitutive properties, however, actual void sizes in materials are often of the order of magnitude of 1 mm^[7], so that a void can easily exist within one grain of a polycrystalline material. Thus an assumption of anisotropic constitutive properties is necessary to better understand void growth at the micron length scale. Recently, crystal plasticity theory has been used to simulate void growth and coalescence, and most of the microstructures, such as grain boundary and crystallographic slip can be taken into account. The influence of plastic anisotropy on damage evolution was investigated by considering the process of creep damage in FCC single crystals^[8]. An elasto-viscoplastic strain gradient crystal plasticity formulation was used to study the deformation of a porous single crystal, and it was found that small voids have the tendency to grow slower than big voids^[9]. The void growth and interaction in FCC copper crystals were studied by employing a rate- dependent formulation of crystal plasticity^[10], and the study illustrated that the rotation of the crystalline lattice and plastic activity on slip systems are concentrated mainly in the ligament region between the voids. A two-dimensional finite element analysis was used to simulate the growth and coalescence of voids by varying void volume fraction, loading state, lattice structure and orientation^[11]. Further investigations showing the influence of different orientations on the deformation behavior were made by HORSTEMEYER et al^[12]. The case of circular void embedded in a single crystal under plane strain conditions was analyzed by slip-line theory^[13]. The deformation and stress fields around a cylindrical void in a single FCC crystal under plane strain condition were derived by using slip line theory^[14]. Void growth and coalescence in FCC single crystals were studied by using crystal plasticity under uniaxial and biaxial loading conditions, in which a 2D plane strain unit cell with one and two cylindrical voids was created^[15]. A 3D unit cell including a spherical void was used to study the effects of crystallographic orientation on void growth and coalescence in single crystals by  LIU et al^[16]. It was found that void growth direction and

shape are significantly dependent on the crystallographic orientation. Though there is some work that simulates the void growth and coalescence in single crystals, little work has been done to address the growth behavior of the void located at grain boundary. In this work, a two- grain model was created to simulate the growth behavior and the plastic deformation distribution around the void, and the effects of the crystallographic orientation and the grain boundary direction with respect to the tensile axis on fracture mode were analyzed as well.

2 Finite element model

A 3D model was created to simulate the growth behavior of the void located at grain boundary, as shown in Fig.1. The axis X is parallel to the sample rolling direction, and the axis Z is parallel to the plate normal direction. The angle of the grain boundary direction with the axis X is defined as θ, and the void at grain boundary is located at the center of the unit cell.

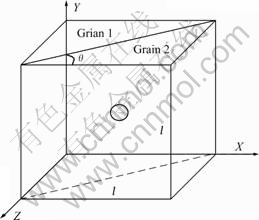
Fig.1 Unit cell for void growth

In FCC crystals, plastic deformation occurs along the {111}<110> family of slip systems, which means 12 potentially active slip systems, as shown in Table 1. Here, the parameter definition and the rate-dependent crystal plasticity constitutive theory are the same as those in Ref.[16], and crystal model of pure aluminum is considered anisotropic elasticity with elasticity of C₁₁=170 GPa, C₁₂=124 GPa, C₄₄=75 GPa^[17], reference slip rate strain rate sensitivity m=0.02, and the hardening parameters: h₀=250 MPa, t₀=16 MPa, t_s=190 MPa, a=2.5 and latent hardening rate q=1.4^[18].

3 Results and discussion

3.1 Void growth in single crystals

If the orientations of grain 1 and grain 2 are just the same, the unit cell in Fig.1 can represent a single crystal. Figs.2-3 show the plastic deformation that characterizes

Table 1 Slip systems in FCC crystals

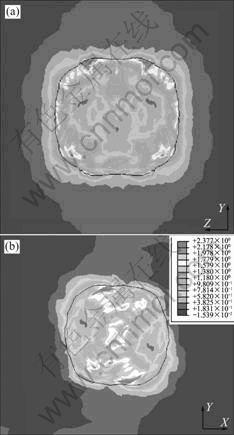
Fig.2 Contour plots of equivalent plastic strain for Bs orientation: (a) YZ section, (b) XY section

the void growth in single crystals in cross sections XY and YZ under the same boundary condition introduced by LIU et al^[16], demonstrating the plastic flow localization and heterogeneous distribution of plastic deformation. Due to anisotropic behavior, void shape has become irregular during deformation, and varies with crystallographic orientation.

Fig.2 indicates that for orientation Bs (35?, 45?, 90?) the peak local plastic strain reaches 2.377 for the corresponding strain in direction X (e_X=0.12). The void rotates and stretches during the deformation, the maximal

void growth direction in plane XY is approximately along 45? to the tensile direction X.

Fig.3 indicates that for orientation Cu (90?, 35?, 45?) the peak local plastic strain reaches 2.625 for the corresponding e_X=0.12. The void rotates and stretches as well during the deformation, and the maximal void growth direction in plane XY is parallel to the axis Y. The maximal plastic strain is localized in the regions that divide the circum of void in plane YZ.

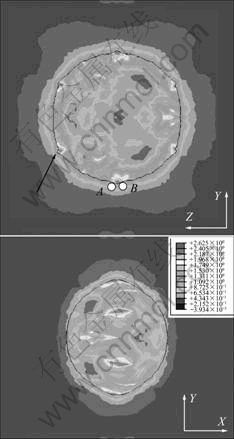
Fig.3 Contour plots of equivalent plastic strain for Cu orientation: (a) YZ section; (b) XY section

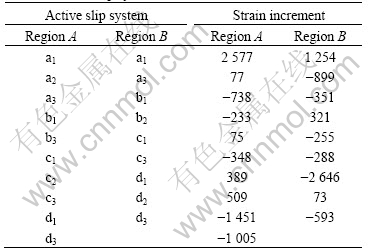
Therefore, void growth direction and shape are quite different for various crystallographic orientations. Furthermore, the corners that are induced around void are observed. NEMAT-NASSER et al^[19] experimentally observed non-circular shapes of the outer and the inner boundaries. NEMAT-NASSER et al^[19] and SOLANKI et al^[20], using both finite element and atomistic methods, revealed that the plastic flow localization induced corner formation along with crack formation and growth. In the present study, the same phenomenon is observed, for example, the position that is pointed by arrow in Fig.3. The void that has an original spherical shape becomes irregular, and induces some corners at which the dislocations will be activated. KYSAR et al^[13] explained the discontinuity in lattice rotation due to plastic deformation through slip-line theory. Table 2 lists the active slip systems and their corresponding shear strain increments (dg) of the last step in calculation for the regions A and B in Fig.3, which may cause the discontinuity around the void on lattice rotating, and form the corner-like region. The rate-dependent crystal plasticity constitutive theory used here assumes that all the 12 active slip systems may be activated, that in this work, the slip system whose shear strain increments is less than 2% maximal shear strain increment is regarded as inactive slip system. Negative sign represents the slip of opposite direction.

Table 2 Active slip systems and their shear strain increment

3.2 Growth behavior of void located at grain boundary

Fig.4 shows the curves of the computed von Mises equivalent stress vs equivalent strain under the uniaxial load parallel to the rolling direction for unit cells without voids for four crystallographic orientations. It is shown that the equivalent stress is almost the same at the equivalent strain for orientations (0?, 45?, 90?) and (0?, 0?, 0?), and increases according to the orders of the orientation (35?, 45?, 90?) and (60?, 45?, 90?).

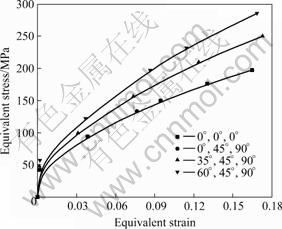
Fig.4 Equivalent stress vs equivalent strain

Fig.5 indicates the equivalent plastic strain of the unit cell with the void located at the grain boundary

between grain 1 and grain 2 at e_X=0.1 in cross section XZ under uniaxial load parallel to the rolling direction, in which the orientations of grain 1 and grain 2 are (0?, 45?, 90?) and (35?, 45?, 90?), and Figs.5 (a)-(c) are the cases for θ=0?, 45? and 60?, respectively. In the case of θ=0?, it can be found in Fig.5(a) that the maximal equivalent plastic deformation is around void in grain 1 (0?, 45?, 90?), which is the soft one of the two grain orientations, and the plastic strain along grain boundary is small. But in the case of θ=45? and 60?, it can be noticed from Figs.5(b) and (c) that the plastic deformation of grain boundary near the void is maximal, and the maximal plastic deformation for q=45? in Fig.5(b) reaches 0.174, which is larger than that for q =60? in Fig.5(c).

Fig.6 shows the equivalent plastic strain of the unit

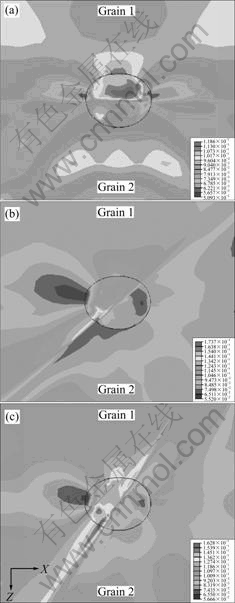
Fig.5 Contour plots of equivalent plastic strain of void located at boundary between grains with orientations of (0?, 45?, 90?) and (35?, 45?, 90?) at e_X=0.1: (a) q =0?; (b) q =45?; (c) q =60?

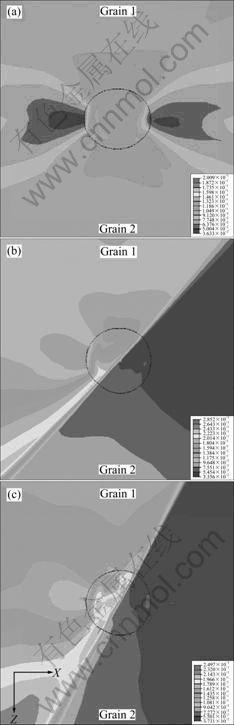
Fig.6 Contour plots of equivalent plastic strain of void located at boundary between grains with orientations of (0?, 45?, 90?) and (60?, 45?, 90?) at e_X =0.1: (a) q =0?; (b) q =45?; (c) q =60?

cell with the void located at the grain boundary between grain 1 and grain 2 (in Fig.1) at e_X=0.1 in cross section XZ under uniaxial loading parallel to the rolling direction, in which the orientations of grain 1 and grain 2 are (0?, 45?, 90?) and (60?, 45?, 90?), and Figs.6(a)-(c) represent the cases for q=0?, 45? and 60?, respectively. The plastic deformation is very similar to that in Fig.5. In the case of q=0?, the plastic deformation of grain boundary near the void is very small. But in the cases of q =45?, 60?, it can be noticed that the plastic deformation of grain boundary near the void is maximal in Figs.6(b) and (c), and the maximal plastic deformation for q=45? and q=60? reaches 0.285 and 0.250, which are larger than those in Figs.5(b) and (c), individually.

The equivalent plastic strain of the unit cell with the void located at the boundary between grains with orientations of (0?, 45?, 90?) and (0?, 0?, 0?) at e_X=0.1 is shown in Fig.7. Figs.7(a)-(c) show the case for q =0?, 45? and 60?, respectively, where the equivalent plastic deformation along grain boundary is small, which is different from that in Figs.5-6. From Fig.4, it can be found that the equivalent stress—strain curves are almost

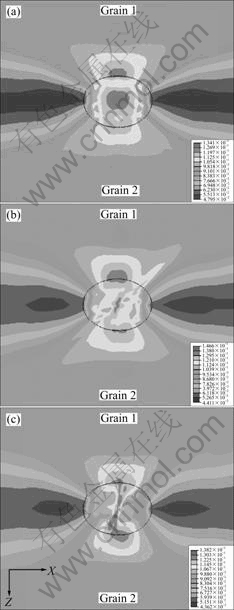
Fig.7 Contour plots of equivalent plastic strain of void located at boundary between grains with orientations of (0?, 45?, 90?) and (0?, 0?, 0?) at e_X =0.1: (a) q =0?; (b) q =45?; (c) q =60?

the same for orientations (0?, 45?, 90?) and (0?, 0?, 0?), that is to say, although with misorientation of 45?, the difference of the orientation factor of the unit cell is small, and small heterogeneous deformation is induced between the two grains.

Figs.5-7 show the equivalent plastic strain distribution of the unit cell with different assemblies of the crystallographic orientation and grain boundary directions q. The results show that in the case of q =0?, the equivalent plastic deformation along grain boundary is small, and the unit cell may fail by transgranular fracture. But in the case of q = 45?, the equivalent plastic deformation of grain boundary near the void is maximal, which may relate to the shear stress of the grain boundary inclining to about 45? to the tensile axis. It is well known that the shear stress of the plane inclining to about 45? to the tensile axis is maximal, and the slip systems of the two grains may be activated easily, which causes large heterogeneous deformation along the grain boundary, and leads to intergranular fracture finally. This can well explain the phenomena observed in experiments by TAKESHI and OSAMU^[21] and MICHAEL and ERHARD^[22] that the grain boundary fracture preferentially occurs at the grain boundary inclining to about 45? to the tensile axis. For the unit cell with the void located at the boundary of orientation (0?, 45?, 90?) and orientation (60?, 45?, 90?), the equivalent plastic deformation along grain boundary is larger than the others, which may relate to large difference of orientation factor of the two grains. Therefore, large heterogeneous deformation occurs between the two grains, which leads to the maximal equivalent plastic deformation among the three unit cells. For the unit cell with the void located at boundary between grains with orientation (0?, 45?, 90?) and (0?, 0?, 0?), in which the difference of orientation factor of the two grains is small, the equivalent plastic deformation along grain boundary is small in the case of q =0?, 45? and 60?, and the unit cell is more likely to fail by transgranular fracture.

4 Conclusions

1) Due to plastic flow localization and anisotropic property, the void with original spherical shape develops an irregular shape during deformation, and sharp corners started from internal surface of void are induced along the grain boundary, and crack nucleates and grows along grain boundary.

2) Under uniaxial load, in the case of q =0?, the equivalent plastic deformation along grain boundary is small, and the unit cell may fail by transgranular fracture. But in the case of q=45?, the equivalent plastic deformation along grain boundary near void is larger than the others, and the unit cell is more likely to fail by intergranular fracture.

3) Under uniaxial load, for the unit cell with the void located at the boundary of orientation (0?, 45?, 90?) and orientation (0?, 0?, 0?), in which the difference of orientation factor is small, the equivalent plastic deformation along grain boundary is small, and unit cell is more likely to fail by transgranular fracture. With increasing difference of orientation factor of the two grains, large heterogeneous deformation may occur between the two grains, which leads to large equivalent plastic deformation along grain boundary, and the intergranular fracture in the unit cell may have more trends to occur.

References

[1] MCCLINTOCK F A. A criterion for ductile fracture by the growth of holes[J]. J App Mech, 1968, 35(3): 363-371.

[2] RICE J R, TRACEY D M. On the ductile enlargement of voids in triaxial stress fields[J]. J Mech Phys Solids, 1969, 17(1): 201-217.

[3] GURSON A L. Continuum theory of ductile rupture by void nucleation and growth (Part I): Yield criteria and flow rules for porous ductile media[J]. J Eng Mat Tech, 1977, 99: 2-15.

[4] TVERGAARD V. Influence of voids on shear band instabilities under plane strain condition[J]. Int J Fracture, 1981, 17(4): 389-407.

[5] TVERGAAD V. On localization in ductile materials containing voids[J]. Int J Fracture, 1982, 18(4): 237-252.

[6] TVERGAAD V, NEEDLE A. Analysis of the cup-cone fracture in a round bar[J]. Acta Metallurgica, 1984, 32(1): 157-169.

[7] DIETER G E. Mechanical metallurgy[M]. New York: McGraw-Hill, 1986.

[8] QI W, BERTRAM A. Anisotropic continuum damage modeling for single crystals at high temperature[J]. Int J Plasticity, 1999, 15(12): 1197-1215.

[9] SHU J Y. Scale dependent deformation of porous single crystals[J]. Int J Plasticity, 1998, 14(10/11): 1085-1107.

[10] ORSINI V C, ZIKRY M A. Void growth and interaction in crystalline materials[J]. Int J Plasticity, 2001, 17(10): 1393-1417.

[11] O'REGAN T L, QUINN D F, HOWE M A, MCHUGH P E, MCHUGH P E. Void growth simulations in single crystals[J]. Comput Mech, 1997, 20(1/2): 115-121.

[12] HORSTEMEYER M F, BASKES M I, GODFREY A. A large deformation atomistic study examining crystal orientation effects on the stress strain relationship[J]. Int J Plasticity, 2002, 18(2): 203-229.

[13] KYSAR J W, GAN Y X, ARAUZA M. Cylindrical void in a rigid-ideally plastic single crystal. Part I: Anisotropic slip line theory solution for face-centered cubic crystals[J]. Int J Plasticity, 2005, 21(8): 1481-1520.

[14] GAN Y X, KYSAR J W, MORSE T L. Cylindrical void in a rigid-ideally plastic single crystal (II): Experiments and simulations[J]. Int J Plasticity, 2006, 22(1): 39-72.

[15] POTIRNICHE G P, HEAMDON J L, HORSTEMEYER M F, LING X W. Lattice orientation effects on void growth and coalescence in fcc single crystals[J]. Int J Plasticity, 2006, 22(6): 921-942.

[16] LIU W H, ZHANG X M, TANG J G, DU Y X. Simulation of void growth and coalescence behavior with 3D crystal plasticity theory[J]. Comput Mater Sci, 2007, 40(1): 130-139.

[17] ANAND L, KOTHARI M. A computational procedure for rate-independent crystal plasticity[J]. J Mech Phys Solids, 1996, 44(4): 525-558.

[18] TANG J G, ZHANG X M, CHEN Z Y, DENG Y L. Simulation influence of inhomogeneous deformation on the development of rolling textures with crystal plasticity finite element[J]. J Cent South University, 2006, 13(2): 117-121.

[19] NEMAT-NASSER S, OKINAKA T, NESTERENKO V, LIU M. Dynamic void collapse in crystals: computational modelling and experiments[J]. Philos Mag A, 1998, 78(5): 1151-1174.

[20] SOLANKI K, HORSTEMEYER M F, BASKES M I. Multiscale study of dynamic void collapse in single crystals[J]. Mech Mater, 2005, 37(2/3): 317-330.

[21] TAKESHI, K, OSAMU I. Ductile fracture in the interior of precipitate free zone in an Al-6.0%Zn-2.6%Mg alloy[J]. Acta Metall, 1976, 24: 817-825.

[22] MICHAEL G, ERHARD H. Observation of ductile intercrystalline fracture of an Al-Zn-Mg-alloy[J]. Acta Metall, 1977, 25: 883-889.

(Edited by CHEN Wei-ping)

Foundation item: Project(2005CB623706) supported by the Major State Basic Research Development Program of China

Received date: 2007-08-28; Accepted date: 2007-10-11

Corresponding author: LIU Wen-hui, PhD; Tel: +86-731-8830265; E-mail: wealth9733221@sohu.com