
J. Cent. South Univ. (2019) 26: 632-639
DOI: https://doi.org/10.1007/s11771-019-4034-6
Fast integrated guidance and control with global convergence
SONG Hai-tao(宋海涛)1, ZHANG Tao(张涛)2
1. High-Tech Institute of Xi’an, Xi’an 710025, China;
2. Department of Automation, Tsinghua University, Beijing 100084, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract:
A global fast convergent integrated guidance and control design approach is proposed. A disturbance observer is utilized to estimate the uncertainties of integrated guidance and control model in finite time. According to the multiple sliding-mode surface control, the independent nonsingular terminal sliding functions are presented in each step, and all the sliding-mode surfaces run parallel. These presented sliding-mode surfaces keep zero value from a certain time, and the system states converge quickly in sliding phase. Therefore, the system response speed is increased. The proposed method offers the global convergent time analytically, which is useful to optimize the transient performance of system. Simulation results are used to verify the proposed method.
Key words:
Cite this article as:
SONG Hai-tao, ZHANG Tao. Fast integrated guidance and control with global convergence [J]. Journal of Central South University, 2019, 26(3): 632–639.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-019-4034-61 Introduction
The response speed of guidance system is the key transient performance of interception system. The improvement of response speed is a useful method against the maneuvering penetration of attacking targets. For the guidance system of interceptor, the guidance law design is an essentially finite-time tracking problem [1]. The convergent speed of closed-loop determines the response speed. However, most of integrated guidance and control (IGC) controllers are asymptotically convergent [2, 3], which means that the convergent time of guidance system is infinite. Then the finite-time convergence of interceptor can provide ways to improve the response speed [4].
The finite-time control is to find a controller so that the system converges to equilibrium point in finite time. For the continuous system, the methods of finite-time control are geometric homogeneity theory, constructive approach based on finite-time Lyapunov function, and terminal sliding-mode technology. There are inequality zooms for the first two methods, and the control law is obtained difficultly. Therefore, the direct relationship between control law and response speed cannot be built. Then in this work, the terminal sliding-mode control is chosen.
The tracking error and its derivatives are used to form the terminal sliding surface, which can ensure the finite-time convergence of system. Compared to the infinite-time control, the system response speed is faster [5–8]. IGC is a high-order system with mismatched/matched uncertainties [9]. There are two ways of terminal sliding-mode design for such a system. One is decoupling [10, 11], which is only applicable to even order systems, and the other gets control recursively [12–15], which is essential serial control that wastes time. And thus these methods cannot be appropriate for IGC.
Recently, there are some studies on the fast convergence of IGC. WANG et al [16] proposed an adaptive nonsingular terminal sliding-mode controller for two-dimensional partial integrated guidance and control (PIGC). The IGC with impact angle constraints was studied [17], in which the presented adaptive multiple-input multiple-output sliding-mode control ensured that the reaching phase of sliding-mode surface was finite-time convergent. To reduce chattering caused by the sign function, a novel sliding-mode control law was developed [18]. A non-singular terminal dynamic surface control was proposed for IGC [19]. However, these research results can only guarantee the partial finite-time convergence. And the explicit equation of convergent time has not been obtained.
Motivated by these discussions, this work considers a global fast convergent controller design for IGC. A disturbance observer is utilized to estimate the uncertainties of IGC model in finite time. According to the multiple sliding-mode surface control method, some independent nonsingular terminal sliding surfaces which run parallel are presented. These presented sliding- mode surfaces keep zero value from a certain time, and the system states converge quickly in sliding phase. Therefore, the system response speed is improved. The proposed method offers the global convergent time analytically, which is useful to optimize the transient performance of IGC system.
The rest of this paper is organized as follows: The control problem is formulated in Section 2. In Section 3, a global fast convergent IGC controller is designed. The performance is analyzed in Section 4. Simulation studies verify the effectiveness of the and proposed method in Section 5, and the conclusions are provided in Section 6.
2 Problem formulation
The IGC model is given as [8]:
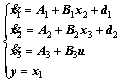 (1)
(1)
where 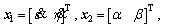
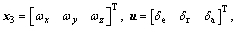
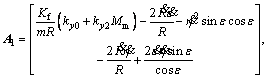

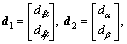
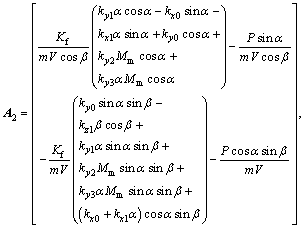
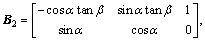
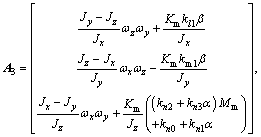

where 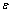 is the line-of-sight angle of inclination;
is the line-of-sight angle of inclination; 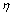 is the line-of-sight angle of declination;
is the line-of-sight angle of declination;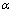 is the attack angle;
is the attack angle;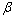 is the sideslip angle; ωx, ωy, ωz, represent rotational angular rates; δe, δr, δa represent the rudder deflection angles; d(·) is uncertainties- equivalent;
is the sideslip angle; ωx, ωy, ωz, represent rotational angular rates; δe, δr, δa represent the rudder deflection angles; d(·) is uncertainties- equivalent;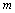 is the mass of interceptor;
is the mass of interceptor; 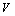 is the speed of interceptor;
is the speed of interceptor; 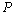 is the rocket thrust; Mm is mach number,
is the rocket thrust; Mm is mach number, is the interceptor-target closing range; Jx, Jy, Jz represent the moments of inertia; Kf and Km represent aerodynamics coefficients; kx(·), ky(·), kz(·), kl(·), km(·), kn(·) represent the fitted aerodynamics coefficients.
is the interceptor-target closing range; Jx, Jy, Jz represent the moments of inertia; Kf and Km represent aerodynamics coefficients; kx(·), ky(·), kz(·), kl(·), km(·), kn(·) represent the fitted aerodynamics coefficients.
By using the parallel approaching method of interception [20, 21], the control objective is accomplished by annihilating the line-of-sight angle rates. Then the main task of IGC is to find a controller which makes the system outputs convergent to zero in finite time.
The following assumption is applied:
Assumption 1: The uncertainty equivalents 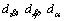 and
and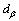 are first order differentiable, and their derivatives have known Lipschitz constants L1,1, L1,2, L2,1 and L2,2.
are first order differentiable, and their derivatives have known Lipschitz constants L1,1, L1,2, L2,1 and L2,2.
3 IGC controller design
The uncertainty equivalents are unknown. To eliminate their influence, the finite-time disturbance observer presented in Refs. [22, 23] is utilized to estimate d1 and d2. This disturbance observer can converge to their true values in finite time. The disturbance observer is:
 (2)
(2)
where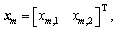
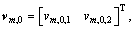
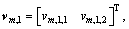
 wm,1=
wm,1=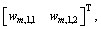
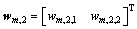 ;
;
λ0, λ1 and λ2 are the observer parameters,and we choose λ0=8, λ1=5, λ2=5. In finite time Tobs, the estimation of d1, d2 is obtained as 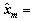
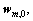
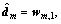
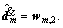 It is found that the observer does not only estimate the uncertainties, but also offers the estimation of system states [24].
It is found that the observer does not only estimate the uncertainties, but also offers the estimation of system states [24].
Then based on multiple terminal sliding-mode control, the IGC controller is given as following.
The tracking errors are given by:
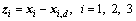 (3)
(3)
and 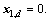
The fast terminal sliding surfaces are defined as [8]:
 (4)
(4)
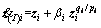 (5)
(5)
where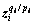 is defined by
is defined by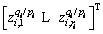 ; ri=2, 2, 3 are the orders of sub-blocks; αi>0; βi>1; pi, qi are odd constants, pi>qi>0.
; ri=2, 2, 3 are the orders of sub-blocks; αi>0; βi>1; pi, qi are odd constants, pi>qi>0.
Step 1: The derivative of s1 is
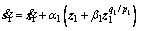
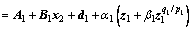 (6)
(6)
The virtual controller is given by

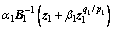 (7)
(7)
where k1,1>0, k1,2>0, and sign(si) is defined as 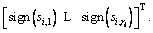
Step 2: The derivative of s2 is
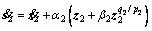
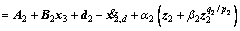 (8)
(8)
The virtual controller is given by
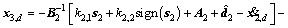
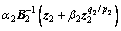 (9)
(9)
where k2,1>0; k2,2>0; 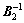 is the right pseudo inverse of
is the right pseudo inverse of  ,
,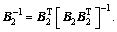
Step 3: The derivative of s3 is given by
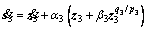
 (10)
(10)
The control input is
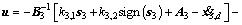
 (11)
(11)
where k3.1>0, k3.2>0.
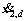 and
and 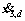 are obtained by [25]:
are obtained by [25]:
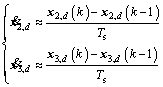 (12)
(12)
where Ts is the system sample time.
4 Performance analysis
Theorem 1: For the fast convergent IGC controller (FCIGC) presented in Section 3. If the controller parameters meet the following conditions 


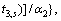
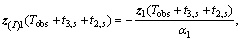 then the system outputs will converge to zero quickly in finite time, and the deign objective is finished, where
then the system outputs will converge to zero quickly in finite time, and the deign objective is finished, where

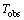
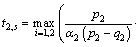
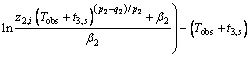
Proof: Choose a Lyapunov function
 (13)
(13)
The time derivative of Vs3 is
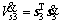
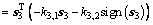
 (14)
(14)
where ||·||1 is the 1-form of vector.
At t=Tobs, according to the definition of terminal sliding surfaces and 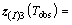
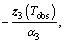 s3=0 and Vs3=0. With Vs3≥0, when t>Tobs,
s3=0 and Vs3=0. With Vs3≥0, when t>Tobs, 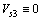 ,
,  That is to say when t>Tobs, the system is kept on the zero-value terminal sliding- mode surface s3=0.
That is to say when t>Tobs, the system is kept on the zero-value terminal sliding- mode surface s3=0.
For the sliding phase, the convergence time of z3,i from  to
to 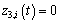 is
is
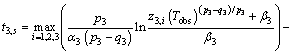
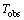 (15)
(15)
Therefore, the sliding time of s3 is t3,s.
When t>Tobs+t3,s,  and then the time derivative of Vs2 is
and then the time derivative of Vs2 is
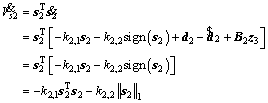
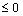 (16)
(16)
With the same method, when t>Tobs+t3,s, 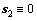 , and the sliding time of s2 is
, and the sliding time of s2 is

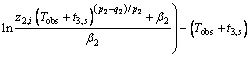 (17)
(17)
When t>Tobs+t3,s, 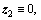 and then the time derivative of Vs1 is
and then the time derivative of Vs1 is
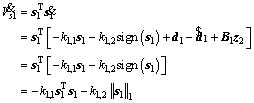
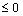 (18)
(18)
With Eqs. (14), (16), and (18), the time derivative of the Lyapunov function (13) is
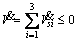 (19)
(19)
Therefore, the IGC controller presented is convergent.
When t>Tobs+t3,s, 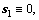 and the sliding time of s1 is
and the sliding time of s1 is


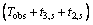 (20)
(20)
When t>Tobs+t3,s+t2,s+t1,s, 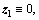 and thus the control objective y=x1=0 is accomplished.
and thus the control objective y=x1=0 is accomplished.
Therefore, the convergent time of IGC system is determined by
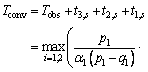
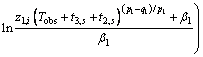 (21)
(21)
It is found that the equation Tconv is analytical, and all the system states are bounded. This completes the proof.
Remark 1: With the convergent time Eq. (21), we can find ways to shorten the convergent time, such as choosing αi, βi larger. This is a useful approach to improve the transient performance of IGC.
5 Simulation results
In this section, the proposed FCIGC controller is tested by simulation studies. Firstly, the parameters of system and those of controller are listed. Then the interception time is tested. Lastly, the comparisons of response speed for different IGC controllers are provided.
5.1 Simulation parameters
The initial conditions of interceptor are V(0)=400 m/s,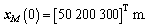 And the initial conditions of target are VT(0)=200 m/s,
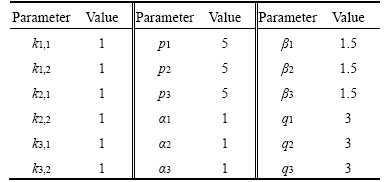
And the initial conditions of target are VT(0)=200 m/s, 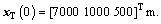 The related controller parameters are shown in Table 1. The interceptor coefficients are given in Ref. [26].
The related controller parameters are shown in Table 1. The interceptor coefficients are given in Ref. [26].
For the disturbance observer, L1,1, L1,2, L2,1, L2,2 can be chosen large arbitrarily to increase the convergent time of observer. In our experiments, L1,1=L1,2=L2,1=L2,2=100. After the other observer parameters are fixed, Tobs is obtained by computersimulation, and it is Tobs=2.3 s for this use.
Table 1 Controller parameters
5.2 Interception time test
The Monte Carlo simulation, which is conducted by 100 sample runs, is used to test the robustness of controller for aerodynamic coefficients.
Figure 1 shows the cumulative distribution of the interception time using the seeker values without noises and the seeker measurements with noises. It is found that there is almost no difference for these seeker data. Therefore, the proposed method has the robustness to the seeker noise. At the same time, approximately  of the cases can be finished successfully in less than 40 s. One typical interception trajectory is given in Figure 2.
of the cases can be finished successfully in less than 40 s. One typical interception trajectory is given in Figure 2.
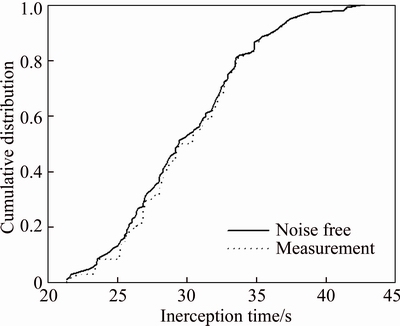
Figure 1 Cumulative distribution of interception time
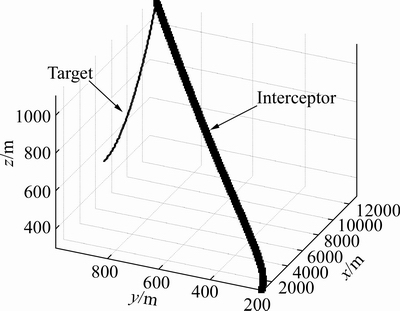
Figure 2 Interception trajectory
5.3 Response speed test
To verify the improvement of response speed, the disturbance observer with derivative-integral terminal sliding mode control (DI-TSMC) in Ref. [12] and PIGC based on adaptive nonsingular terminal sliding mode control (ANTSMC) in Ref. [16] are used to compare with FCIGC.
First, an interception task with the given parameters is used for the comparison of response speed. The line-of-sight angular rates are shown in Figures 3 and 4. The response time of FCIGC is shortest, and that of ANTSMC is longest. The reason is that DI-TSMC uses the optimized terminal sliding control and ANTSMC adopts the original terminal sliding control for the planar IGC.
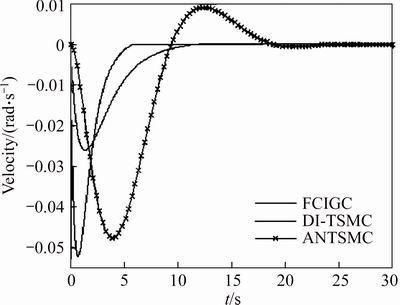
Figure 3 Line-of-sight angular velocities of inclination
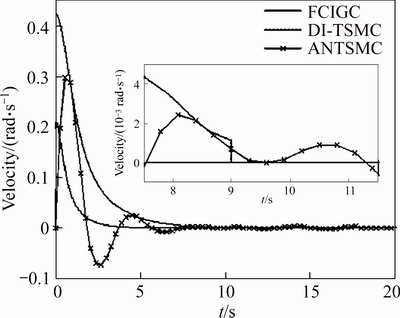
Figure 4 Line-of-sight angular velocities of declination
Second, the shortest distance, in which the interception cannot be influenced by target maneuvers, is tested. With the noise-free seeker values, the different amplitudes and different maneuver distances of step target maneuvers are chosen. The target maneuvering amplitudes are chosen as g, 5g and 10g, where g presents over load, and the components in different axis are the same. The distance for target maneuvering is varied in [300, 2250] m with the step length 50 m.
The miss distance of FCIGC with different target maneuvers are shown in Figure 5. The higher the maneuver amplitude is, the larger the miss distance is. And the longer the distance for target maneuvering is, the less the miss distance is. It is found that when the distance for target maneuvering is above 700 m, the final miss distance is nearly the same. DI-TSMC and ANTSMC methods have the similar conclusions, as shown in Figures 6 and 7. The critical maneuver distances are 1000 m and 1800 m respectively. These results demonstrate that FCIGC has the fastest response speed.
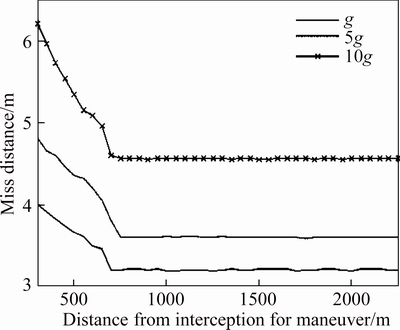
Figure 5 Sensitivity to target maneuvers for FCIGC
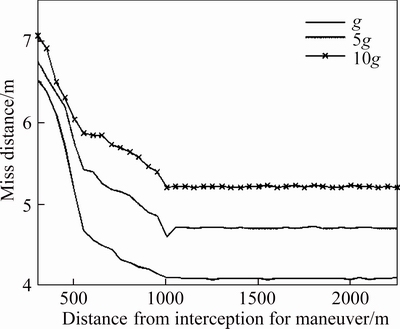
Figure 6 Sensitivity to target maneuvers for DI-TSMC
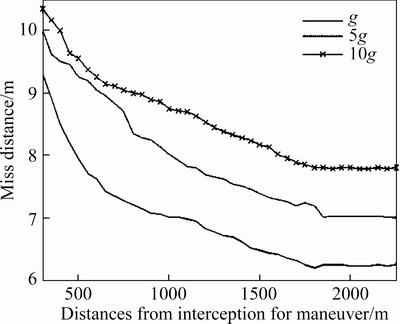
Figure 7 Sensitivity to target maneuvers for ANTSMC
6 Conclusions
This study proposes a design method of IGC with global fast convergence to improve the response speed of interceptor. The finite-time disturbance observer and multiple terminal sliding- mode surfaces control are utilized. The system certainties are estimated precisely by disturbance observer in finite time. Based on the multiple sliding-mode surfaces control, the nonsingular terminal sliding-mode surfaces are designed independently in each step, and run parallel. Since a certain time, the designed surfaces keep zero, and the sliding phase ensures fast convergence. Therefore, the timeliness is improved. The proposed method guarantees the finite-time global convergence of IGC system states, and thus the convergent time of line-of-sight angle rates is obtained analytically. How to choose the controller parameters to minimize the convergent time is a future study.
References
[1] HE Shao-ming, LEE Chang-Hun. Optimality of error dynamics in missile guidance problems [J]. Journal of Guidance, Control, and Dynamics, 2018, 41(7): 1624–1633. DOI: http://dx.doi.org/10.2514/1.G003343.
[2] YAN Han, WANG Xing-hu, YU Bing-feng, JI Hai-bo. Adaptive integrated guidance and control based on backstepping and input-to-state stability [J]. Asian Journal of Control, 2014, 16(2): 602–608. DOI: http://dx.doi.org/ 10.1002/asjc.682.
[3] LEVY M, Shima T, GUTMAN S. Single versus two-loop full-state guidance and control [J]. Journal of Guidance, Control, and Dynamics, 2017, 40(8): 1968–1977. DOI: http://dx.doi.org/10.2514/ 1.G002722.
[4] MA Yi-wei, ZHANG Wei-hua. Differential geometric guidance command with finite time convergence using extended state observer [J]. Journal of Central South University, 2016, 23(4): 859–868. DOI: 10.1007/s11771- 016-3133-x.
[5] ZAK M. Terminal attractors for addressable memory in neural networks [J]. Physics Letters A, 1988, 133(1): 18–22. DOI: http:// dx.doi.org/10.1016/0375-9601(88)90728-1.
[6] ZHANG F, DUAN G R. Integrated translational and rotational finite-time maneuver of a rigid spacecraft with actuator misalignment [J]. Control Theory & Applications, IET, 2012, 6(9): 1192–1204. DOI: http://dx.doi.org/10.1049/ iet-cta. 2011.0413.
[7] MAN Zhi-hong, YU Xing-huo. Terminal sliding mode control of MIMO linear systems [J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 1997, 44(11): 1065–1070. DOI: http://dx.doi. org/10.1109/81.641769.
[8] SONG Hai-tao, ZHANG Tao. Fast robust integrated guidance and control design of interceptors [J]. IEEE Transactions on Control Systems Technology, 2016, 24(1): 349–356. DOI: http://dx.doi.org/10.1109/TCST.2015. 2431641.
[9] HE Shao-ming, SONG Tao, LIN De-fu. Impact angle constrained integrated guidance and control for maneuvering target interception [J]. Journal of Guidance, Control, and Dynamics, 2017, 40(10): 2653–2661. DOI: http://dx.doi.org/ 10.2514/1.G002201.
[10] Bayramoglu H, Komurcugil H. Nonsingular decoupled terminal sliding-mode control for a class of fourth-order nonlinear systems [J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(9): 2527–2539. DOI: http://dx.doi.org/10.1016/j.cnsns.2012. 11.008.
[11] Bayramoglu H, Komurcugil H. Time-varying sliding coefficient based terminal sliding mode control methods for a class of fourth-order nonlinear systems [J]. Nonlinear Dynamics, 2013, 73(3): 1645–1657. DOI: http://dx.doi.org/10.1007/s11071-013-0892- x.
[12] Chiu C S. Derivative and integral terminal sliding mode control for a class of MIMO nonlinear systems [J]. Automatica, 2012, 48(2): 316–326. DOI: http://dx.doi.org/ 10.1016/j.automatica.2011.08.055.
[13] FENG Yong, YU Xing-huo, HAN Feng-ling. On nonsingular terminal sliding-mode control of nonlinear systems [J]. Automatica, 2013, 49(6): 1715–1722. DOI: http://dx.doi.org/ 10.1016/j.automatica. 2013. 01. 051.
[14] FENG Yong, YU Xing-huo, HAN Feng-ling. High-order terminal sliding-mode observer for parameter estimation of a permanent-magnet synchronous motor [J]. IEEE Transactions on Industrial Electronics, 2013, 60(10): 4272–4280. DOI: http://dx.doi.org/10.1109/TIE.2012.22135 61.
[15] ZHUANG Kai-yu, SU Hong-ye, ZHANG Ke-qin, CHU Jian. Adaptive terminal sliding mode control for high-order nonlinear dynamic systems [J]. Journal of Zhejiang University Science, 2003, 4(1): 58–63. DOI: http://dx. doi.org/10.1631/jzus.2003.0058.
[16] WANG Xiang-hua, WANG Jin-zhi. Partial integrated missile guidance and control with finite time convergence [J]. Journal of Guidance, Control, and Dynamics, 2013, 36(5): 1399–1409. DOI: http://dx.doi.org/10.2514/1.58983.
[17] WANG Xiang-hua, WANG Jin-zhi. Partial integrated guidance and control for missiles with three-dimensional impact angle constraints [J]. Journal of Guidance, Control, and Dynamics, 2014, 37(2): 644–657. DOI: http://dx. doi.org/10.2514/1.60133.
[18] WANG Xiang-hua, WANG Jin-zhi. Partial integrated guidance and control with impact angle constraints [J]. Journal of Guidance, Control, and Dynamics, 2015, 38(5): 925–936. DOI: http://dx.doi.org/10.2514/1.G000141.
[19] ZHANG Cong, WU Yun-jie. Non-singular terminal dynamic surface control based integrated guidance and control design and simulation [J]. ISA Transactions, 2016, 63: 112–120. DOI: https://doi.org/ 10.1016 /j.isatra.2016.03.013.
[20] Shima T, Golan O M. Exo-atmospheric guidance of an accelerating interceptor missile [J]. Journal of the Franklin Institute, 2012, 349(2): 622–637. DOI: http://dx.doi.org/10. 1016/j.jfranklin. 2011.06.024.
[21] SONG Hai-tao, ZHANG Tao, ZHANG Guo-liang, LU Chang-jie. Integrated interceptor guidance and control with prescribed performance [J]. International Journal of Robust and Nonlinear Control, 2015, 25(16): 3179–3194. DOI: http://dx.doi.org/10.1002/ rnc.3260.
[22] SHTESSEL Y B, Shkolnikov I A, Levant A. Smooth second-order sliding modes: Missile guidance application [J]. Automatica, 2007, 43(8): 1470–1476. DOI: http://dx.doi.org/ 10.1016/ j.automatica.2007.01.008.
[23] YANG Jun, LI Shi-hua, SU Jin-ya, YU Xing-huo. Continuous nonsingular terminal sliding mode control for systems with mismatched disturbances [J]. Automatica, 2013, 49(7): 2287–2291. DOI: https://doi.org/10.1016/j.automatica. 2013.03.026.
[24] Levant A. Universal output-feedback SISO controllers [J]. Asian Journal of Control, 2003, 5(4): 484–497. DOI: 10.1111/ j.1934-6093.2003.tb00166.x.
[25] HEDRICK J K, YIP P P. Multiple sliding surface control: Theory and application [J]. Journal of Dynamic Systems, Measurement, and Control, 2000, 122(4): 586–593. DOI: http://dx.doi.org/10.1115/ 1.1321268.
[26] SONG Hai-tao, ZHANG Tao, ZHANG Guo-liang. L1 adaptive state feedback controller for three-dimensional integrated guidance and control of interceptor [J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2014, 228(10): 1693–1701. DOI: http://dx.doi.org/10.1177/09544100135 06332.
(Edited by FANG Jing-hua)
中文导读
快速全局收敛的制导控制一体化设计
摘要:本文提出一种全局快速收敛的制导控制一体化设计方法。利用干扰观测器对一体化模型中的不确定性进行有限时间精确估计;基于多滑模面控制方法,在每一步提出独立的非奇异终端滑模函数,且这些滑模面并行运行,从某时刻起滑模面保持零值,系统状态在滑动阶段快速收敛。因此,系统反应速度提高。所设计的方法提供系统全局收敛时间的解析表达式,有利于优化系统的动态性能。仿真结果验证了该方法的优越性。
关键词:制导控制一体化;全局收敛;干扰观测器;多滑模面控制
Foundation item: Project(61673386) supported by the National Natural Science Foundation of China; Project(2018QNJJ006) supported by the High-Tech Institute of Xi’an, China
Received date: 2018-03-15; Accepted date: 2018-09-03
Corresponding author: SONG Hai-tao, PhD, Lecturer; Tel: +86-15389433783; E-mail: songht1018@163.com; ORCID: 0000-0001-9942-4230
Abstract: A global fast convergent integrated guidance and control design approach is proposed. A disturbance observer is utilized to estimate the uncertainties of integrated guidance and control model in finite time. According to the multiple sliding-mode surface control, the independent nonsingular terminal sliding functions are presented in each step, and all the sliding-mode surfaces run parallel. These presented sliding-mode surfaces keep zero value from a certain time, and the system states converge quickly in sliding phase. Therefore, the system response speed is increased. The proposed method offers the global convergent time analytically, which is useful to optimize the transient performance of system. Simulation results are used to verify the proposed method.


