弹流润滑效应下直齿轮的接触疲劳寿命

胡贇^{1, 2}，刘少军^{1, 2}，丁晟^{1, 2}

(1. 中南大学 机电工程学院，湖南 长沙，410083；

2. 中南大学 高性能复杂制造国家重点实验室，湖南 长沙，410083)

摘 要：

动态啮合过程用7个典型的啮合状态进行离散，得到7个不同啮合状态下弹流润滑油膜压力的精确数值解。通过有限元法，将此油膜压力转化为齿轮的接触应力。在综合考虑Goodman零均值应力转化公式、P-S-N曲线的横向影响因素以及Miner疲劳累积损伤理论的EM修正法则后，建立齿轮的P-S-N曲线，计算得到弹流润滑效应下直齿轮的接触疲劳寿命，其结果是干Hertz接触的3.91倍，是GB/T 3480—1997标准的10.4倍。对比结果表明：对高速传动直齿轮进行接触疲劳寿命的准确评估，有必要考虑弹流润滑效应，同时现行齿轮接触疲劳寿命评估方法偏于保守。

关键词：

弹流润滑；直齿轮；接触疲劳寿命；

中图分类号：TH114          文献标志码：A         文章编号：1672-7207(2014)12-4187-07

Contact fatigue life on spur gear with consideration of elastohydrodynamic

HU Yun^{1, 2}, LIU Shaojun^{1, 2}, DING Sheng^{1, 2}

(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;

2. State Key Laboratory for High Performance Complex Manufacturing,

Central South University, Changsha 410083, China)

Abstract: Continuous dynamic meshing process of spur gear was divided into seven typical meshing states. Accurate numerical solutions of elastohydrodynamic lubrication oil film pressure in different meshing states were obtained. Oil film pressure was converted to gear contact stress by finite element method. P-S-N curve of gear was established with the consideration of Goodman formula, influence factors of P-S-N curve and EM modify rule. Contact fatigue life of spur gear with consideration of elastohydrodynamic was calculated. The result is 3.91 times longer than that of dry Hertz contact, and 10.4 times than that of GB/T3480—1997. The results show that consideration of elastohydrodynamic is essential for an accurate contact fatigue life evaluation of high-speed gear, the present evaluation method of gear contact fatigue life is conservative.

Key words: elastohydrodynamic; spur gear; contact fatigue life

随着现代机械传动系统不断地向高速、重载的方向发展，齿轮的受载条件以及润滑状态都会明显异于低速、轻载的齿轮。其中一个非常重要的物理现象便是在高速运转下啮合齿面间形成的弹流润滑效应^[1]。对于不考虑弹流润滑效应的齿轮接触疲劳寿命，一般采用三齿啮合模型来模拟齿轮的传动，再结合相关的疲劳寿命研究理论进行接触疲劳寿命评估^[2-3]。对于考虑弹流润滑效应的齿轮接触疲劳寿命，Zaretsky^[4]将齿轮的接触疲劳寿命类比于轴承的接触疲劳寿命，以Lundberg和Palmgern 在滚动轴承计算中使用过的统计方法为理论基础，润滑效应的考虑则通过引入ISO281:2007标准中关于轴承润滑修正系数选取的方法来实现；Li等^[5-6]通过弹性力学中的接触理论计算了弹流润滑效应下接触区次表面的应力分布，采用Susmel和Lazzarin准则完成接触疲劳寿命的预测；高创宽^[7]、亓秀梅等^[8]、潘登^[9]以及张增强^[10]采用弹性力学中的接触理论分别分析了弹流润滑效应下油膜比厚、齿面粗糙度、齿轮转速以及润滑油黏度对接触区次表面应力的影响，并根据这个结果来判定这些因素对寿命的影响；Deng等^[11]通过一系列试验，给出了油润滑下齿面温度的计算公式，认为齿轮的疲劳寿命应以齿面温度为计算基础而非赫兹应力。本文作者则致力于开展综合考虑弹流润滑效应以及齿轮几何形状的影响，通过有限元分析获取齿轮接触应力，再结合材料P-S-N曲线来进行弹流润滑效应下直齿轮的接触疲劳寿命评估的研究，将所得结果与基于Hertz接触理论和GB/T 3480—1997标准的齿轮接触疲劳寿命评估结果作比较，研究弹流润滑效应对齿轮接触疲劳寿命的影响程度。

1  齿轮弹流润滑物理模型的建立

针对直齿轮弹流润滑问题的研究，可通过一对圆柱体的接触来模拟直齿轮啮合^{[7, 12]}，这对圆柱体的半径则分别等同于齿轮啮合点处渐开线的当量曲率半径R₁和R₂，转动速度分别等同于相应齿轮的转速n₁和n₂，啮合点的切线速度分别为u₁和u₂。如图1(a)所示。如果进一步转化，可以用1个当量半径为R、转速为n，切线速度为u的等效圆柱体和1个无限长的刚性平面的接触来模拟，如图1(b)所示。

2  齿轮接触应力分析

2.1  齿轮啮合过程的几何参数计算

某直升机主减速器中的一对啮合直齿轮基本参数如下：模数m=3.5 mm，传动比i=3.218 75，齿数z₁=32，z₂=103，齿宽b_g=45 mm，压力角α=22.5°。工况取转速n=7 500 r/min，传递功率P_E=600 kW，齿轮副材料20Cr₂Ni₄A，屈服强度σ_s=1 080 MPa，拉伸强度σ_b=1 175 MPa，弹性模量E=2.07×10⁵ MPa，泊松比ν=0.29，润滑油动力黏度η=0.014 Pa·s。

考虑齿轮重合度以及渐开线几何特性给弹流润滑计算参数带来的变化，可以在雷诺方程中引入时间项来完成轮齿在单个啮合周期内瞬态弹流润滑数值解^[13]。但通过分析齿轮的啮合变化规律后，本文将齿轮的整个啮合过程用图2所示的5个特殊啮合点来表示：啮入点A、双单啮合交替点B(进一步分析，此点可以表示为1个双齿啮合的瞬态B_-和1个单齿啮合的瞬态B₊)、节点J、单双啮合交替点C(与B点同理，此点可以表示为1个单齿啮合的瞬态C_-和1个双齿啮合的瞬态C₊)、啮出点D，采用稳态的一维形式的雷诺方程进行求解。

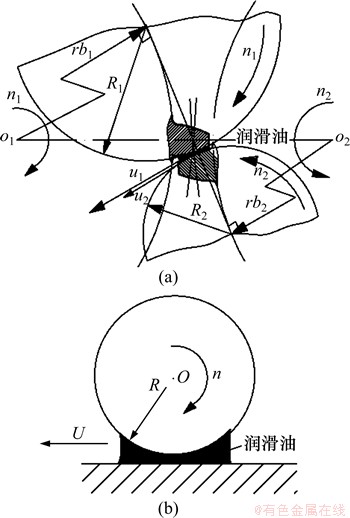
图1  齿轮弹流润滑物理模型

Fig. 1  Physical models of gear EHD

图2  齿轮啮合过程图

Fig. 2  Gear meshing process

现对这些特殊啮合点的几何参数进行计算。

1) 主动轮转角计算分析。实际啮合长度为

  (1)

式中：r_a1和r_a2分别为主、从动轮的齿顶圆半径；r_b1和r_b2分别为主、从动轮的基圆半径；r₁和r₂分别为主、从动轮的分度圆半径。

主动轮单齿啮合转过的角度为

            (2)

式中：p_b为齿轮的法向齿距。

主动轮双齿啮合转过的角度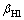为

           (3)

主动轮从基圆处到进入啮合转过的角度为

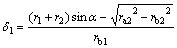      (4)

主动轮从啮入点A到节点J转过的角度为

            (5)

2) 啮合点处的单位齿宽载荷w。齿轮从渐开线的A处到渐开线的D处，齿轮啮合经历了双单齿的交替过程，因而其单位齿宽载荷的计算在渐开线不同位置亦有所区别，计算公式如下：

           (6)

式中：k为同时啮合的齿轮对数。

3) 啮合点处的综合曲率半径R。以A点为例，其余点只需代入对应的数值即可完成计算。

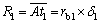            (7)

          (8)

              (9)

4) 啮合点处的齿面平均速度为

(i=1，2)    (10)

              (11)

啮合过程的几何参数计算结果如表1所示。

2.2  弹流润滑油膜压力的计算

假设润滑油为牛顿流体，处于等温线接触弹流润滑状态。建立1个x轴为表面卷吸速度方向，y轴为油膜压力的坐标系。弹流润滑基本方程组如下。

1) Reynolds方程为

        (12)

式中：ρ和η分别为润滑油的密度和黏度；u为齿面平均速度；p和h分别表示油膜的压力和厚度。

Reynolds方程求解的边界条件为

2) 膜厚方程。膜厚方程包括初始间隙、中心膜厚以及弹性变形等，其形式为

    (13)

式中：h₀为待定常数；R为综合曲率半径；E′为综合弹性模量；s为任意分布载荷p(s)与坐标原点的距离。

3) 黏压方程。黏压方程采用Reolands公式

表1  齿轮啮合过程的几何参数计算结果

Table 1  Results of geometric parameters of gear meshing process

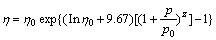     (14)

式中：η₀为大气压下的黏度；p₀为压力系数；z为矿物油系数，一般可取0.68。

4) 密压方程。密压方程采用Dowson和Higginson形式

           (15)

式中：ρ₀为润滑油的环境密度。

5) 载荷方程为

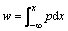               (16)

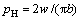为减少上述方程组的未知数个数，引入以下7个无量纲参数p=p/p_H，X=x/b，H=hR/b²，ρ^*=ρ/ρ₀，η^*=η/η₀，U^*=η₀u/(E′R)，W=w/(E′R)。其中：b为赫兹接触半宽， ；p_H为最大Hertz接触应力， ，将这些量纲1的参数代入弹流润滑方程组，简化后进行弹流润滑数值解的求解^[14]。

弹流润滑油膜压力计算结果如图3所示。图3所示为齿轮沿啮合线弹流润滑油膜压力曲线的变化趋势。从齿根到齿顶，出口压力峰值位置先往出口处移动，过了节点J之后，出口压力峰值的位置则开始往入口处移动。在单齿啮合的情形下(B₊，J和C_-)，出口压力峰值相对中心油膜压力而言，其值较小，而在双齿啮合的情形下(A，B_-，C₊，D)，出口压力峰值相对中心油膜压力而言，其值较大，即重载有助于抑制出口压力的形成，而轻载的情形下容易形成较大的出口油膜压力。图4所示为B₊点沿齿宽方向的油膜压力分布三维图。

图3  弹流润滑油膜压力计算结果

Fig. 3  Calculation results of EHD for oil film pressure

图4  B₊点油膜压力沿齿宽分布

Fig. 4  Distribution of oil film pressure along gear width on point B₊

2.3  接触应力的转化

假定油膜在该工况下稳定存在，不发生破裂。图4所示为B₊点油膜压力沿齿宽分布。考虑油膜压力在赫兹接触变形区呈不规则变化(图4)，为最大限度的表现油膜压力作用在齿轮表面上的情形。图5所示为划分加载面。分别以上述各啮合点为中心，以赫兹接触区为油膜压力加载区域，并将此加载区域沿赫兹接触宽度等分成5块狭长的加载面^[15-16](图5)。该点处的油膜压力取赫兹接触区内的计算结果作为施加条件，用同样的方法分成5等分，对每个小部分的油膜压力求平均值，再将这个油膜压力的平均值作为加载区域的外载荷。通过有限元分析，即可得出油膜压力作用下齿轮的接触应力。

为对结果进行比较，对干赫兹接触状态以及GB/T 3480—1997下的接触应力也分别进行计算，结果如表2所示。干赫兹接触应力采用赫兹接触公式进行计算。干赫兹接触公式只考虑了载荷与等效半径的影响，而弹流润滑下的齿轮接触应力还考虑了润滑因素的影响。由于弹流润滑和干赫兹接触状态下的最大接触应力都发生在B₊点处，而齿轮实际最先容易发生接触疲劳的位置也是处于节线靠近齿根附近的区域，因而接触应力计算结果分布情况符合实际情形。

图5  划分加载面

Fig. 5  Division of loading surface

表2  不同条件下的接触应力

Table 2  Contact stress under different conditions  MPa

3  疲劳分析

3.1  平均应力修正

材料P-S-N曲线一般是在指定应力比为-1的情形下进行的疲劳试验，应力均值为0。实际上齿轮齿面的接触应力为脉动循环，既有应力幅值又有非零的应力均值，这与试验情形不一样。因此，有必要将此类应力修正为试验情形下的应力。常用的做法是采用Goodman曲线、Gerber曲线、Soderberg曲线等寿命曲线进行修正。一般认为，线性Goodman曲线修正非零均值应力的交变载荷其值具有一定的保守性和安全性，且为线性形式，简单实用。基于安全性考虑，本文针对航空齿轮的寿命评估选用线性Goodman曲线进行平均应力修正，其表达式如下：

             (17)

式中：S_a为应力幅值；S_m为应力均值；σ_b为材料的拉伸强度；σ_eqv为等效疲劳应力。

3.2  建立齿轮P-S-N曲线

在以双对数坐标系绘制的P-S-N曲线内，其有限寿命方程近似为1条斜线，方程的通用形式为

           (18)

式中：N_p为与存活率有关的疲劳寿命，a_p和b_p为与存活率有关的材料常数。

从文献[17]中得20Cr₂Ni₄A材料的中值接触疲劳寿命曲线方程为

(σ_eqv≥1474 MPa)             (19)

然而，式(19)是针对20Cr₂Ni₄A材料的标准试件进行的接触疲劳试验，齿轮零件和材料试件又由于结构、尺寸以及加工等方面的差异，因此，还应考虑到应力集中系数k_t、尺寸系数ε以及表面加工系数β等三项因素对齿轮疲劳强度产生的影响。据文献[18]，取横向因素k_t=1.3，ε=0.76，β=1。修正后的等效疲劳应力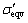为

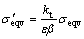              (20)

最终齿轮有限寿命内的P-S-N曲线可以表示为

(σ_eqv≥862 MPa)             (21)

3.3  Miner线性累积损伤理论的修正

Miner线性累积损伤理论认为损伤是线性的，且可以进行累加，一般指定累积损伤度为“1”时，构件发生失效破坏。

由于该理论简便而在工程上得到广泛应用，但由于该理论认为处于疲劳极限以下的应力对于构件的损伤为零^[19]，而实际上这些微小的大量循环载荷同样是造成构件疲劳失效的一个主要因素，为使结果不偏于危险，需要对该理论进行修正。常用的Miner修正理论有OM法则、EM法则、MM法则，但出于安全性考虑，航空工业采用EM法则完成线性累积损伤理论的修正。即在双对数坐标系中，对处于疲劳极限以下的应力仍以相同的b_p斜率向下延伸，最终齿轮的P-S-N曲线如图6所示。

3.4  接触疲劳寿命结果分析

由于齿轮的接触疲劳寿命取决于接触应力最大处， GB/T3480—1997标准条件下以节点J为计算点，弹流润滑效应和赫兹接触条件以B₊为计算点。根据本文提出的接触疲劳寿命研究方案与成果，弹流润滑、干赫兹接触以及GB/T 3480—1997下的齿轮接触疲劳寿命计算结果如表3所示。

结果表明：弹流润滑效应下的齿轮接触疲劳寿命是干赫兹接触下齿轮接触疲劳寿命的3.91倍，是GB/T 3480—1997寿命的10.4倍。究其原因，是由于考虑了弹流润滑效应后，齿面间的接触应力受油膜压力与形状的影响，在一定程度上得到了均化，并且齿面啮合过程中的最大接触应力也由于油膜的影响而降低。该分析结果可以从表2中的计算结果得到证实。而在P-S-N曲线方程中，接触应力恰恰是影响接触疲劳寿命计算值大小的一个重要因素。

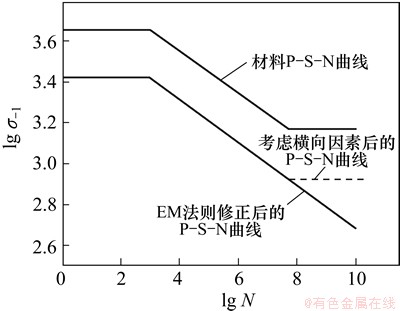
图6  不同情形下的P-S-N曲线

Fig. 6  P-S-N curve under different modify rules

表3  齿轮接触疲劳寿命

Table 3  Gear contact fatigue life

4  结论

1) 现行基于干Hertz接触和GB/T 3480—1997标准的齿轮接触疲劳寿命预测方法没有考虑润滑因素的影响，但由于高速传动齿轮间存在弹流润滑效应，物体间的接触方式发生了改变。

2) 通过与本文考虑弹流润滑效应后进行的齿轮接触疲劳寿命评估结果比较，传统齿轮接触疲劳寿命计算结果偏于保守，不能完全反映齿轮实际工作能力，对高速传动部件而言，其使用范围具有一定的局限性。

参考文献：

[1] 温诗铸, 黄平. 摩擦学原理[M]. 北京: 清华大学出版社, 2008: 21-43.

WEN Shizhu, HUANG Ping. Principles of tribology[M]. Beijing: Tsinghua University Press, 2008: 21-43.

[2] 史妍妍. 基于热分析的附件机匣若干可靠性问题研究[D]. 沈阳: 东北大学机械工程学院, 2009: 16-33.

SHI Yanyan. Study on accessory gearbox reliability based on thermal analysis[D]. Shengyang: Northeastern University. College of Mechanical Engineering, 2009: 16-33.

[3] 林腾蛟, 沈亮, 赵俊渝. 风电增速箱输出级齿轮副疲劳寿命有限元分析[J]. 重庆大学学报, 2012, 35(1): 1-6.

LIN Tengjiao, SHEN Liang, ZHAO Junyu. Fatigue life finite element analysis of output gear pair of wind turbine speed-increase gearbox[J]. Journal of Chongqing University, 2012, 35(1): 1-6.

[4] Zaretsky E V. Design of oil-lubricated machine components for life and reliability[R]. Poland: Glenn Research Center, 2007: 1-10.

[5] LI Sheng. Lubrication and contact fatigue models for roller and gear contacts[D]. Ohio: The Ohio State University. Department of Mechanical and Aerospace Engineering, 2009: 150-177.

[6] LI Sheng, Kahraman A, Klein M. A fatigue model for spur gear contacts operating under mixed elastohydrodynamic lubrication conditions[J]. Journal of Mechanical Design, 2012, 134: 1-11.

[7] 高创宽. 渐开线齿轮传动的混合弹流润滑研究[D]. 太原: 太原理工大学机械工程学院, 2005: 34-85.

GAO Chuangkuan. Study of involute gearing mixed elastohydrodynamic lubrication[D]. Taiyuan: Taiyuan University of Technology. College of Mechanical Engineering, 2005: 34-85.

[8] 亓秀梅, 高创宽. 基于真实粗糙齿面的齿轮传动接触应力分析[J]. 润滑与密封, 2011, 36(9): 24-29.

QI Xiumei, GAO Chuangkuan. Analysis of gearing contact fatigue stress based on actual surface roughness profiles[J]. Lubrication Engineering, 2011, 36(9): 24-29.

[9] 潘登. 齿轮转速对齿轮传动接触疲劳寿命影响的研究[D]. 太原: 太原理工大学机械工程学院, 2010: 47-61.

PAN Deng. Research on effect of rotational speed on gearing contact fatigue life[D]. Taiyuan: Taiyuan University of Technology. College of Mechanical Engineering, 2010: 47-61.

[10] 张增强. 润滑油黏度对齿轮接触疲劳寿命影响的研[D]. 太原: 太原理工大学机械工程学院. 2008: 43-60.

ZHANG Zhengqiang. Study on the effect of lubricant’s viscosity on geared fatigue life[D]. Taiyuan: Taiyuan University of Technology. College of Mechanical Engineering, 2008: 43-60.

[11] Deng G, Nakanishi T. Evaluation of surface fatigue strength based on surface temperature (Surface temperature calculation for rolling-sliding contact)[J]. JSME International Journal, Series C, 2001, 44(1): 217-222.

[12] Carmen A B C. An elastohydrodynamic lubrication model for helicopter high-speed transmission components[D]. Ohio: The University of Toledo. College of Engineering, 2004: 1-6.

[13] 王文中, 操鸿, 胡纪滨. 渐开线斜齿轮非稳态弹流润滑数值模拟研究[J]. 摩擦学学报, 2011, 31(6): 604-609.

WANG Wengzhong, CAO Hong, HU Jibin. Numerical simulation of transient elastohydrodynamic lubrication of helical gears[J]. Tribology, 2011, 31(6): 604-609.

[14] 黄平, 骆建斌, 温诗铸. 一种数值求解弹流润滑油膜和压力的新方法[J]. 润滑与密封, 1998(6): 10-14.

HUANG Ping. LUO Jianbin. WEN Shizhu. A new numerical approach for calculating EHL film thickness and pressure[J]. Lubrication Engineering, 1998(6): 10-14.

[15] 李华奎. 汽车驱动桥的可靠性与弹流润滑下齿轮的有限元析[D]. 青岛: 青岛理工大学机械工程学院, 2012: 21-42.

LI Huakui. Reliability analysis of the truck rear axle and finite element analysis of the gear under the EHL[D]. Qingdao: Qingdao Technological University. Mechanical Engineering, 2012: 21-42.

[16] 张延化. 弹流润滑状态下风力发电机增速齿轮的有限元分析[D]. 青岛: 青岛理工大学机械工程学院, 2009: 35-59.

ZHANG Yanhua. Finite element analysis of accelerating gear of wind-power-generating under the EHL[D]. Qingdao: Qingdao Technological University. Mechanical Engineering, 2009: 35-59.

[17] 朱法义, 蔡成红, 闫牧夫, 等. 20Cr₂Ni₄A钢稀土渗碳的组织与齿轮的接触疲劳强度[J]. 金属热处理学报, 1994, 15(4): 31-37.

ZHU Fayi, CAI Chenghong, YAN Mufu, et al. Microstructure and gear contact fatigue strength of steel 20Cr₂Ni₄A carburized with rare earth[J]. Journal of Metal Heat Treatment, 1994, 15(4): 31-37.

[18] 徐灏. 疲劳强度[M]. 北京: 高等教育出版社, 1988: 111-129.

XU Hao. Fatigue strength[M]. Beijing: High Education Press, 1988: 111-129.

[19] 易当祥, 刘春和, 吕国志, 等. 自行火炮行动系统关重件的疲劳寿命仿真[J]. 兵工学报, 2007, 28(2): 138-143.

YI Dangxiang, LIU Chunhe, L Guozhi, et al. Fatigue life simulation of key components of running gear for a self-propelled gun[J]. ACTA Armamenta RIT, 2007, 28(2): 138-143.

(编辑  陈爱华)

收稿日期：2014-02-12；修回日期：2014-05-26

基金项目(Foundation item)：总装预研基金资助项目(8130208)(Project (8130208) supported by Assembly Research Foundation)

通信作者：胡贇(1988-)，男，江西吉安人，博士研究生，从事疲劳寿命与可靠性研究；电话：18874206674；E-mail：hyfatigue@163.com

摘要：将直齿轮的连续动态啮合过程用7个典型的啮合状态进行离散，得到7个不同啮合状态下弹流润滑油膜压力的精确数值解。通过有限元法，将此油膜压力转化为齿轮的接触应力。在综合考虑Goodman零均值应力转化公式、P-S-N曲线的横向影响因素以及Miner疲劳累积损伤理论的EM修正法则后，建立齿轮的P-S-N曲线，计算得到弹流润滑效应下直齿轮的接触疲劳寿命，其结果是干Hertz接触的3.91倍，是GB/T 3480—1997标准的10.4倍。对比结果表明：对高速传动直齿轮进行接触疲劳寿命的准确评估，有必要考虑弹流润滑效应，同时现行齿轮接触疲劳寿命评估方法偏于保守。