
![]()

Trans. Nonferrous Met. Soc. China 22(2012) 935-942
Isothermal kinetics of mechanochemically and thermally synthesized Ag from Ag2O
Gholam Reza KHAYATI1, Kamal JANGHORBAN2, Mohamad Hosein SHARIAT2
1. Department of Materials Science and Engineering, Shahid Bahonar University of Kerman, Kerman, Iran;
2. Department of Materials Science and Engineering, School of Engineering,Shiraz University, Zand Avenue, Shiraz, Iran
Received 3 August 2011; accepted 2 November 2011
Abstract:
The kinetics of isothermal reduction of Ag2O with graphite under argon atmosphere for a non-activated sample and mechanically activated sample was investigated. It is found that Johnson–Mehl–Avrami model appropriately explained the thermal and mechanochemical synthesis of Ag from Ag2O+ghraphite mixture. The process kinetics was investigated using the same approach for milled and unmilled samples. The results show that the Avrami exponent of mechanochemical reduction is higher than that of high temperature thermal reduction. Also, the mechanisms of nuclei growth in thermal and mechanochemical reduction are diffusion controlled and interface controlled, respectively.
Key words:
isothermal kinetics; mechanochemical activation; thermal reduction; Johnson–Mehl–Avrami model; Ag;
1 Introduction
Mechanical activation and mechanochemistry is a very useful technique for preparing metals, metastable phases and intermetallics in the nano scale regime. Solid state reactions involve the formation of a new phase at the interfaces of the reactants. Increasing of the product phases involves diffusion of the reactant atoms through the product phases, which consist of a barrier layer avoiding further diffusion. Consequently, high temperature is needed for the reaction to take place at a reasonable rate. Also, formation of fresh surfaces and increasing structural defects as well as decreasing particle size can increase the reaction kinetics [1].
From an operative point of view, the mechanochemical activation by ball milling is a very useful method and has advantageous such as easy to control and no need of costly reactants. But it suffers from conceptual principles. Some of the most important restrictions are ambiguity of the mechanism during the activation and appropriate identification of reaction route [1,2]. Thus, the reaction kinetics in the intermediate stages of ball milling attracts attention in the field of solid state reaction.
In solid state reactions, appropriate kinetic equations, rate limiting steps and estimation of kinetic parameters could supply a deeper conception into the possible mechanisms of transformation [3]. Effects of mechanical activation on the kinetics of solid-state transformation have been investigated by others, including reactions between metals [4], thermal decomposition of mechanically activated compounds [2,5-7], leaching of mechanically activated compounds [8-10], and synthesis of solid solution and/or amorphous compounds by ball milling [11-15]. To the best of our knowledge, correlation of activation energies and mechanisms of transformation as a function of milling time has not been thoroughly investigated. These investigations are appreciated for the ability to control solid-state reactions and for describing the mechanochemistry of inorganic solids. The authors previously studied the probability of mechanochemical reduction of silver oxide with graphite [16], but the kinetics of mechanochemical and thermal reduction of mechanically activated powder mixtures have not been investigated yet.
This research was carried out to find detailed descriptions of the influence on mechanochemical activation of Ag2O reduction with graphite. Moreover, in order to find the mechanism of the reactions in mechanochemical and thermal reduction, the kinetic behavior of both processes was compared.
2 Experimental
Starting materials were pure Ag2O powder (99% purity, 5-40 μm, Merck) and graphite (99.9% purity, 10-50 μm, Merck). The milling process was performed in a high energy planetary ball mill. Details of ball milling process are given in Table 1. Ag2O with 40% (mole fraction) of extra carbon was reduced according to reaction (1):
2Ag2O+C→4Ag+CO2↑ (1)
Reaction products were tested by XRD (PhilipsPW-1730) using Cu Kα radiation. The degree of structure disorder during milling, F, is estimated from relation (2) [2]:
F=Bt/B0 (2)
where Bt is the equivalent integral width of the intensity profiles of disordered sample after milling time t and B0 is the equivalent integral width of the ordered sample. B can be estimated according to Eq. (3).
B=A/Imax (3)
where A is the area under the X-ray diffraction peak whose the maximum intensity is Imax.
To evaluate the kinetics parameters, unmilled sample and three samples milled for 2, 4 and 6 h were exposed to isothermal reduction tests. 2 g of each sample was pressed in a cylindrical mould to obtain a density of about 1.50 g/cm3. The drying process of pressed samples was carried out under argon atmosphere at 100 ℃ for 3 h. Thermal analyses of dried samples were performed under flowing argon using a NETZSCH STA 449F3 device equipped with thermogravimetric system and an Al2O3 crucible at a rate of 50 ℃/min. The flow rate of argon was adjusted to 500 mL/min. The thermal reduction of samples was carried out at 200, 220, 240, 260 and 280 ℃, for 5-90 min. To monitor the reaction progress, the mass changes of samples were continuously registered. The conversion degree (α) of reaction after time t, in each sample was estimated according to Eq. (4) [7]:
α=(w0–w)/(w0-wf) (4)
where w0, w and wf are the initial, actual and final sample masses for complete reduction of Ag2O according to Reaction (1).
3 Results and discussion
3.1 Isothermal reduction kinetics analysis
Figure 1 shows the α—t curves of milled and unmilled samples at different temperatures. As shown, milling process has a significant effect on the reduction kinetics of Ag2O, especially at 200 and 220 ℃. For example, the conversion degree of reaction after 90 min of thermal reduction at 200 ℃ for unmilled sample was 0.09, whereas at the same temperature this value increased to about 0.65 for sample with 6 h milling, showing that by increasing milling time, the reduction rate increased.
Basically, the kinetic models of solid state reactions can be divided into three categories: 1) models in which the controlling step is diffusion of reactants or diffusional models, 2) models in which the administrated mechanism is chemical reaction at the interphase of reactant-product and 3) models in which the reaction rate is determined by nucleation and growth. To find appropriate reaction mechanisms, several kinetic models were tested to the experimental α—t curves [17]. The mathematical functions of models were checked for linear fit and the obtainable parameters of each suggested model are listed in Table 2.
It was necessary to note that the conversion degree of reaction, especially at 200 and 220 ℃, was lower than 0.5 and consequently, application of the reduced time plots for the reaction models (in which α was plotted as a function of t/t0.5, where t0.5 was the time for α=0.5) was impossible to determine the suitable kinetic model [18]. However, the same strategy based on classical kinetic models was applied to this work.
The results of fitting α—t curve for different samples with kinetics model (Table 2) showed that the only linear fit was obtained by the Johnson–Mehl–Avrami (JMA) model and other tested models were shown in logarithmic-type curves. Hence, it was concluded that the JMA model (Eq. (5)) approximately satisfied the reaction kinetic. This equation explains governing mechanisms of a broad variety of solid state reactions [19]:
α(t)=1-exp[-(kt)n] (5)
where t is the time; n is the Avrami exponent, which depends on the growth mechanism and the geometry of powder [19]; the value of n gives information on what conversion mechanisms are involved during the phase transformation, providing that the phase conversion proceeds by nucleation and growth models [20]; k is the reaction rate constant. Large values of k imply high reaction rates. Hence, the values of n and k supply a clue to the type of reaction mechanisms which control the transformation and also demonstrate how fast these mechanisms work [12]. As shown in Table 2, Eq. (5) is generally used to evaluate practical data by means of a logarithmic plot, where ln[-ln(1-α)] is plotted versus lnt (the Avrami plots). The slope and intercept of the resulting straight line are n and n lnk, respectively.
Table 1 Details of ball mill machine and milling conditions

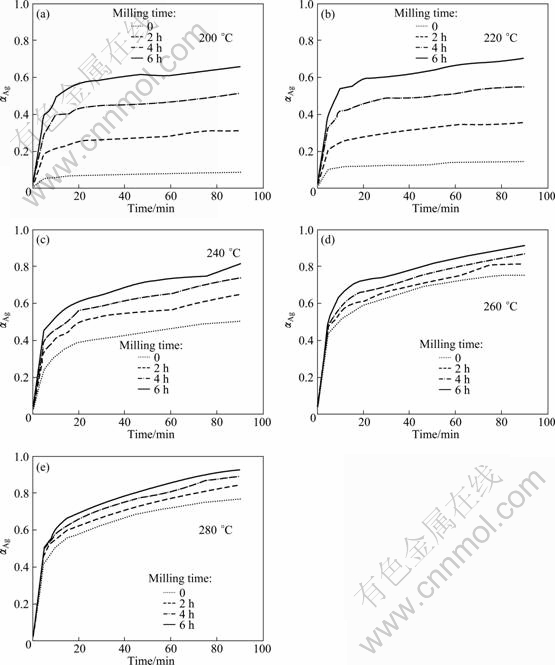
Fig. 1 Conversion degree of reaction for different samples with various annealing time at different temperatures: (a) 200 ℃; (b) 220 ℃; (c) 240 ℃; (d) 260 ℃; (e) 280 ℃
Table 2 Kinetic models used for fitting experimental conversion degree of reaction versus time
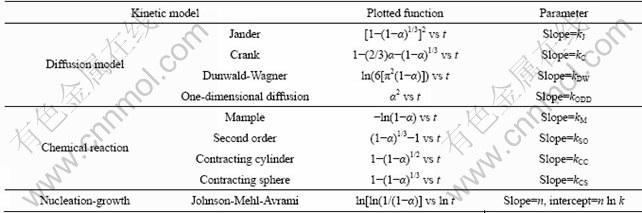
Avrami plots of each sample are shown in Fig. 2. The calculated values of n and k are listed in Table 3. All the values of n are less than 2.5, which proposes that the reduction reaction of Ag2O was diffusion controlled [12,21]. Also, at any constant temperature the values of n and k increase by increasing milling time. The increasing rate of k at low temperature is more significant. As an example, mechanical activation of the samples heated at 200 ℃ for 6 h increased the k value from 1.83×10-9 to 1.64×0-2 min-1. Moreover, higher values of n for more activated mixtures suggest that mechanical activation increased nucleation sites. This may be related to the fact that the structure was refined to nanoscale regions during milling and caused several structural defects which were appropriate nucleation sites [16]. The activation energy of transformation was calculated using the Arrhenius equation of reaction rate constant in the logarithmic form:
ln k=ln A-Ea/(RT) (6)
where A is a constant (called as pre-exponential or frequency factor); Ea is the activation energy; R is the gases constant; T is the absolute temperature. Figure 3 displays the changes of lnk as a function of T-1 for each activated mixture. Ea can be determined from the slope of lines in each temperature range. The estimated values of apparent activation energy of the reduction reaction in various conditions are listed in Table 4.

Fig. 2 Avrami plot of ln[-ln(1-α)] vs ln t for mixtures with different milling time at different temperatures: (a) 200 ℃; (b) 220 ℃; (c) 240 ℃; (d) 260 ℃; (e) 280 ℃
Table 3 Calculated values of kinetics parameters of mixtures at various temperatures according to Avrami equation
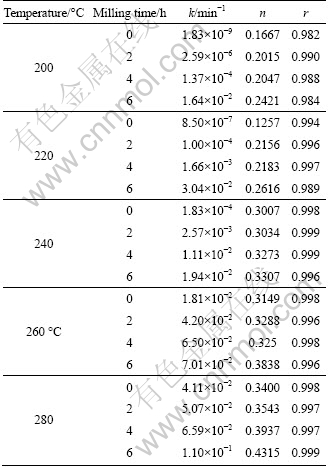
Figure 3 shows a change in the apparent activation energy of transformation at 260 ℃ which is shown by the changes of slope. This may be illustrated by reduction of diffusion paths prepared by decreasing particle sizes and creation of lattice defects in the particles by mechanical activation. Also, increasing the surface area, SA, and the amount of structural disorder, F (Eq. (2)) by increasing the milling time is another reason of this behavior.
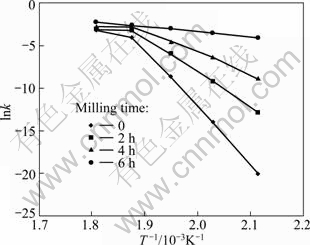
Fig. 3 Arrhenius plots for thermal reduction of Ag2O with carbon at temperature of 200-280 ℃
Table 4 Apparent activation energy of samples

Figure 4 shows the changes of structural disorder as a function of milling time. It can be found that up to 6 h of milling, the F value intensifies by 5.6 times. Generally, the effects of SA and F have been expressed by a practical coefficient in the form of SAF as Eq. (7):
k=a+bSAF (7)
where a and b are constants. According to Fig. 4, F increases with milling time and as a result increased k values are obtained. Moreover, thermal reduction of Ag2O was a heterogeneous transformation and so increasing SA increased the rate of reaction.

Fig. 4 Effect of milling time on structural disorder of Ag2O
3.2 Kinetics modeling of mechanochemical reduction during room temperature milling
Analysis of XRD patterns of samples with different milling time (Fig. 5) reveals the phase changes of samples with milling time prolonging. As shown in Fig. 5, by increasing milling time, the peaks of Ag2O are slowly broadened and their intensities reduce. The diffraction peak locating at 2θ=44.3° of the 3 h-milled sample obviously proposes the existence of Ag. Further milling increases the Ag peak intensities and single phase Ag is prepared after 22 h of milling.
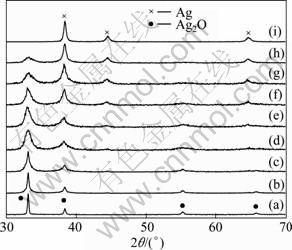
Fig. 5 XRD patterns of mixtures with milling time of 0 h (a), 1 h (b), 2 h (c), 3 h (d), 6 h (e), 12 h (f), 16 h (g), 19 h (h) and 22 h (i)
Figure 6 shows the measured values of the conversion degree of reaction as a function of milling time for mechanochemical preparation samples. In this case the values of α are calculated by [22]:
α=1-(It/I0) (8)
where It is the Ag2O (111) peak intensity of sample milled for a certain time and I0 is the intensity of Ag2O (111) peak of unmilled sample. Figure 6 shows that there is an incubation time of almost 3 h after which the reduction reaction begins with a sharp rising rate. The rate of the reaction decreases slowly with increasing milling time. Furthermore, the first incubation period probably equals the grain refinement and mixing phenomena. It should be noted that due to the insufficient amount of XRD resolution, the characteristic peaks of Ag could not be probably observed. So, the real incubation time may be less than 3 h and little amounts of Ag are reduced sooner than 3 h.
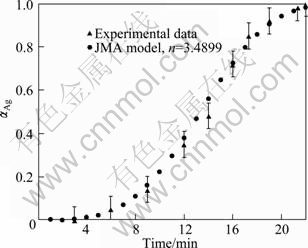
Fig. 6 Relative fraction of silver prepared with various milling time at room temperature compared with JMA model corresponding to mean Avrami exponent of 3.4899
To choose an appropriate reaction model, several kinetic models (Table 2) were examined to obtain α—t curves. The most accurate linear fit was obtained by the Johnson–Mehl–Avrami (JMA) model. Hence, the JMA model was appropriately applied for kinetics modeling of this process. The Avrami plot for mechanochemical preparation of Ag according to the experimental value of α in Fig. 6 is shown in Fig. 7. It is necessary to note that α value is assumed to be zero until 3 h of milling, and Avrami plot begins afterward. The Avrami exponent, n, is estimated as 3.4899 (Fig. 7), which proposes that the mechanism of mechanochemical preparation of Ag is interface controlled growth [22,23]. For comparison, α value is plotted vs time in Fig. 6. It shows that the JMA model appropriately describes the kinetics of mechanochemical preparation of Ag.
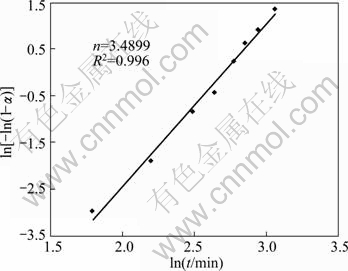
Fig. 7 Avrami plot for mechanochemical formation of Ag
It should be mentioned that, the irregularity was probably from the inaccuracy of XRD measurements, especially up to 3 h milling. Considering the value of n equaled to 3.4899 and using Avrami plot, the reaction rate constant, k=0.06732 min-1 is estimated. Thus, the kinetics equation for mechanochemical reduction of Ag2O to Ag using ball milling may be proposed as:
α(t)=1-exp[-(0.06732t)3.4899] (9)
where t is the milling time in min and α is the conversion degree of reaction.
3.3 Comparison of kinetics modeling of high temperature thermal reduction and mechano- chemical reduction
Since solid state reactions progressed at the interface of reactant-product, the reaction rate is related to the surface area of the unreacted part of the mixture as well as nucleation phenomena. The lower Avrami exponents of high temperature thermal reduction strongly imply that the particles are covered by a layer of the final product in the first stages and the transformation progressed by diffusion-controlled mechanism in three dimensions, where nucleation is disrupted. From other point of view, in mechanochemical reduction of Ag2O, grain size decreases during ball milling, and increases interphase boundaries and structural defects, which accelerate the reduction reaction [16]. Hence, the larger number of nucleation sites and shorter diffusion routes enhance the reduction reaction compared with the high temperature thermal reduction. Moreover, milling could continuously eliminate layers from the surface of particles. Thus, the mechanochemical reduction of Ag2O is interface controlled growth [22,23].
Analysis of both processes proposes that although various activation parameters resulted in different reaction rates, the phase conversion progressed by nucleation and growth model. Accordingly thermal and mechanical activation increase Avrami exponent and reduce diffusion barriers. Therefore, the interaction of various reaction pathways may be related to the different periods whose activation parameters could overcome the barriers. As an example, the rate of nucleation sites by mechanical activation is much higher than thermal activation, while elimination of chemical interface reaction barrier by thermal activation is easier than mechanical activation. In thermal activation, diffusion coefficient changes exponentially with temperature. While, mechanical activation decreases the diffusion paths by creation of defects and eliminating product surface layer between particles. Diffusion controlled growth and interface controlled growth, respectively, are the two conversion mechanisms involved during the thermal and mechanochemical reduction that the phase conversion proceeded by nucleation and growth model.
4 Conclusions
1) The JMA model appropriately explained the thermal and mechanochemical preparation of Ag from Ag2O+ghraphite mixture. Because of continuous formation of structural defects and grain boundaries as well as activated fresh surface areas during the milling which were appropriate sites for nucleation of Ag, the Avrami exponent of mechanochemical reduction is higher than that of high temperature thermal reduction.
2) The modeling results reveal that different activation parameters result in various reaction rates, but the phase conversion proceeds by nucleation and growth model. Also, the mechanisms of growth in thermal and mechanochemical reduction are diffusion controlled and interface controlled, respectively.
References
[1] SURYANARAYANA C, IVANOV E, BOLDYREV VV. The science and technology of mechanical alloying [J]. Mater Sci Eng A, 2001, 304-306: 151–158.
[2] BAL?? P. Extractive metallurgy of activated minerals [M]. Amsterdam: Elsevier, 2000.
[3] TOMASHEVITCH K V, KALININ S V, VERTEGEL A A, OLEINIKOV N N, KETSKO V A, TRETYAKOV Y D. Application of non-linear heating regime for the determination of activation energy and kinetic parameters of solid-state reactions [J]. Thermochim Acta, 1998, 323: 101-107.
[4] AIKIN B J M, COURTNEY T H, MAURICE D R. Reaction rates during mechanical alloying [J]. Mater Sci Eng A, 1991, 147: 229-237.
[5] BOTTA P M, AGLIETTI E F, PORTO L?PEZ J M. Kinetic study of ZnFe2O4 formation from mechanochemically activated Zn–Fe2O3 mixtures [J]. Mater Res Bull, 2006, 41: 714-723.
[6] HU H, CHEN Q, YIN Z, ZHANG P, ZOU J, CHE H. Study on kinetics of thermal decomposition of mechanically activated pyrites [J]. Thermochim Acta, 2002, 389: 79-83.
[7] VLAEV L T, GEORGIEVA V G, GOSPODINOV G G. Kinetics of isothermal decomposition of ZnSeO3 and CdSeO3 [J]. J Therm Anal Calorim, 2005, 79: 163-168.
[8] BAL?? P. Mechanical activation in hydrometallurgy [J]. Int J Miner Process, 2003, 72: 341-354.
[9] FICERIOVA J, BALAZ P, BOLDIZAROVA E. Thiosulfate leaching of gold from a mechanically activated CuPbZn concentrate [J]. Hydrometallurgy, 2002, 67: 37-43.
[10] AMER A M. Alkaline pressure leaching of mechanically activated Rosetta ilmenite concentrate [J]. Hydrometallurgy, 2002, 67: 125-133.
[11] LIU Y J, CHANG I T H. The correlation of microstructural development and thermal stability of mechanically alloyed multicomponent Fe-Co-Ni-Zr-B alloy [J]. Acta Mater, 2002, 50: 2747-2760.
[12] SHEN Y, HNG H H, OH J T. Formation kinetics of Ni–15% Fe–5% Mo during ball milling [J]. Mater Lett, 2004, 58: 2824-2828.
[13] DELOGU F, MONAGHEDDU M, MULAS G, SCHIFFINI L, COCCO G. Some kinetic features of mechanical alloying transformation processes [J]. J Non-crystalline Solids, 1998, 232-234: 383-389.
[14] BRAGANTI J P H, HELD O, KUHNAST F A, ILLEKOVA E. Kinetic study of isothermal crystallization in amorphous Al33Ni16Zr51 produced by mechanical alloying [J]. Thermochim Acta, 2000, 362: 71-78.
[15] YAN Zhi-jie, DANG Shu-e, WANG Xiang-hui, LIAN Pei-xia. Applicability of Johnson-Mehl-Avrami model to crystallization kinetics of Zr60Al15Ni25 bulk amorphous alloy [J]. Transactions of Nonferrous Metals Society of China, 2008, 18: 138-144.
[16] KHAYATI G R, JANGHORBAN K. The nanostructure evolution of Ag powder synthesized by high energy ball milling [J]. J Adv Powder Technol. (in press)
[17] GALWEY A K, BROWN M E. Thermal decomposition of ionic solids [M]. Amsterdam: Elsevier, 1999: 75-110.
[18] SHARP J H, BRINDLEY G W, NARAHARI ACHAR B N. Numerical data for some commonly used solid state reaction equations [J]. J Am Ceram Soc, 1966, 49: 379-382.
[19] CHRISTIAN J W. The theory of transformation in metals and alloys [M]. Oxford (UK): Elsevier Science Ltd., 2002.
[20] NARLIKAR A. Studies of high temperature superconductors: Advances in research and applications [M]. Nova Publishers, Technology & Engineering, 2001: 48.
[21] SHEU H, HSIUNG L, SHEU J. Synthesis of multiphase intermetallic compounds by mechanical alloying in Ni–Al–Ti system [J]. J Alloys Compd, 2009, 469: 483-487.
[22] JACKSON KA. Kinetic processes: Crystal growth, diffusion, and phase transitions in materials [M]. Wiley-VCH, 2010: 209.
[23] PAPON P, LEBLOND J, MEIJER PHE. The physics of phase transitions: concepts and applications [M]. Springer-Verlag Berlin Heidelberg, 2006: 52.
Ag2O机械活化和热还原合成Ag的等温动力学
Gholam Reza KHAYATI1, Kamal JANGHORBAN2, Mohamad Hosein SHARIAT2
1. Department of Materials Science and Engineering, Shahid Bahonar University of Kerman, Iran;
2. Department of Materials Science and Engineering, School of Engineering,Shiraz University, Zand Avenue, Shiraz, Iran
摘 要:在氩气气氛下,将Ag2O与石墨通过机械活化或热还原反应生成Ag,对其等温还原过程的动力学进行研究。结果表明,采用Johnson–Mehl–Avrami模型能合理地解释Ag2O与石墨经机械活化和热还原合成Ag的过程。采用相同的模型来研究机械活化和热还原反应合成Ag的动力学时,机械活化还原过程中的Avrami指数比热还原的要高;热还原和机械活化过程中的晶核长大机制分别是扩散控制和界面控制。
关键词:等温动力学;机械化学活化;热还原,Johnson–Mehl–Avrami模型;银
(Edited by LI Xiang-qun)
Corresponding author: Gholam Reza Khayati; Tel: +98-915-1903477; Fax: +98-341-2114053; E-mail: khayati@shirazu.ac.ir; rezakhayyati@yahoo.com
DOI: 10.1016/S1003-6326(11)61267-3
Abstract: The kinetics of isothermal reduction of Ag2O with graphite under argon atmosphere for a non-activated sample and mechanically activated sample was investigated. It is found that Johnson–Mehl–Avrami model appropriately explained the thermal and mechanochemical synthesis of Ag from Ag2O+ghraphite mixture. The process kinetics was investigated using the same approach for milled and unmilled samples. The results show that the Avrami exponent of mechanochemical reduction is higher than that of high temperature thermal reduction. Also, the mechanisms of nuclei growth in thermal and mechanochemical reduction are diffusion controlled and interface controlled, respectively.


