
J. Cent. South Univ. (2020) 27: 3364-3374
DOI: https://doi.org/10.1007/s11771-020-4552-2
Temporal consistency maintenance on multiprocessor platforms with instance skipping
BAI Tian(白天), LI Zhi-jie(李志杰), FAN Bo(范波)
School of Information Science and Engineering, Hunan Institute of Science and Technology,Yueyang 414000, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract:
Maintaining temporal consistency of real-time data is important for cyber-physical systems. Most of the previous studies focus on uniprocessor systems. In this paper, the problem of temporal consistency maintenance on multiprocessor platforms with instance skipping was formulated based on the (m,k)-constrained model. A partitioned scheduling method SC-AD was proposed to solve the problem. SC-AD uses a derived sufficient schedulability condition to calculate the initial value of m for each sensor transaction. It then partitions the transactions among the processors in a balanced way. To further reduce the average relative invalid time of real-time data, SC-AD judiciously increases the values of m for transactions assigned to each processor. Experiment results show that SC-AD outperforms the baseline methods in terms of the average relative invalid time and the average valid ratio under different system workloads.
Key words:
cyber-physical systems; sensor transactions; multiprocessor scheduling; temporal consistency;
Cite this article as:
BAI Tian, LI Zhi-jie, FAN Bo. Temporal consistency maintenance on multiprocessor platforms with instance skipping [J]. Journal of Central South University, 2020, 27(11): 3364-3374.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-020-4552-21 Introduction
Cyber-physical systems (CPSs) are used in many application domains that need to process real-time data in a timely manner [1-3]. Examples of real-time data include the position of a vehicle and the temperature of an engine. A real-time data object is temporally consistent (or temporally valid) if its latest value truly reflects the current status of the corresponding entity in the system environment [4]. Sensor transactions are generated to sample the status of entities and refresh the data values. They should be effectively scheduled to maintain the temporal consistency of real-time data; otherwise, the systems cannot make responses to environment change timely.
In recent years, there have been a number of works on temporal consistency maintenance. XIONG et al [4] proposed the More-Less scheme (ML) which adopts the periodic task model and the deadline monotonic scheme (DM) to schedule sensor transactions. XIONG et al [5] proposed the DS-FP method which reduces the processor workload by judiciously deferring the release times of transaction instances. The DS-FP method was extended in Ref. [6] to be a dynamic priority scheduling algorithm named DS-EDF by applying the earliest deadline first (EDF) policy for update jobs scheduling. XIONG et al [7] proposed three algorithms to derive the periods and deadlines of sensor transactions under EDF. LI et al [8] proposed a two-phase algorithm to reduce the searching cost of period and deadline assignment under EDF. HAN et al [9] studied the problem of maintaining temporal consistency in the presence of mode changes. Two mode switch points searching algorithms were presented. All above methods are designed for uniprocessor systems.
LI et al [10] proposed several algorithms to partition a set of sensor transactions on multiprocessors under EDF and DM. The resource augmentation bounds of these algorithms were also derived. ZHOU et al [11] proposed efficient methods to maintain temporal consistency while reducing energy cost on multicore platforms. The co-scheduling of update and control transactions on multiprocessor platforms was studied in Ref. [12]. Several partitioned scheduling algorithms were given. KANG [13] adopted the global EDF algorithm and the Half-Half scheme (HH) to satisfy the data validity constraints.
The works described above consider providing a complete guarantee on temporal consistency. This may be hard to achieve when the system workload is unpredictable or there is severe resource competition between different types of transactions. The feedback control method was applied in Refs. [14-18] to support the desired quality of data objects and quality of user transactions. XIONG et al [19] proposed a set of extensions of ML to achieve the trade-off between QoS of temporal consistency and the number of supported transactions. Scheduling algorithms, based on fixed priority scheduling, EDF and DS-LALF, were presented in Refs. [20-22] to meet the deadlines of all user transactions while maximizing the quality of data objects. KANG [23] presented an effective approach to decrease both the deadline miss ratio and power consumption by real-time query aggregation and data freshness adaptation. These works are all limited to uniprocessor systems.
In this paper, the problem of maintaining temporal consistency of real-time data objects on multiprocessor platforms is studied. The (m, k)- constrained model is used for instance skipping to provide a certain degree of temporal consistency. The major contributions of the paper are as follows:
1) The problem of temporal consistency maintenance on multiprocessor platforms with instance skipping was formulated based on the (m, k)-constrained model.
2) A partitioned scheduling method SC-AD was proposed to solve the problem. SC-AD minimizes the average relative invalid time of real-time data by judiciously determining the values of m for each sensor transaction and assigning the transactions to processors.
3) The performance of the proposed method was evaluated through experiments. It is shown that SC-AD outperforms the baseline methods in terms of the average relative invalid time and the average valid ratio.
2 System model
Let X={Xi}1≤i≤n denote a set of real-time data and Г={τi}1≤i≤n a set of sensor transactions. The data object Xi is associated with a validity interval Vi. Sensor transaction τi is used to update the value of Xi. The computation time of τi is Ci. The jitter between the sampling time and the release time of a transaction instance is assumed to be zero. Transactions are sorted by the shortest validity first (SVF) scheme [4], i.e., Vi ≤ Vj if i < j.
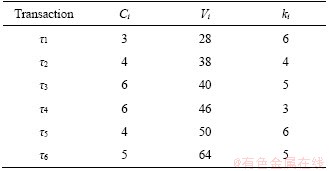
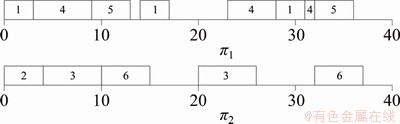
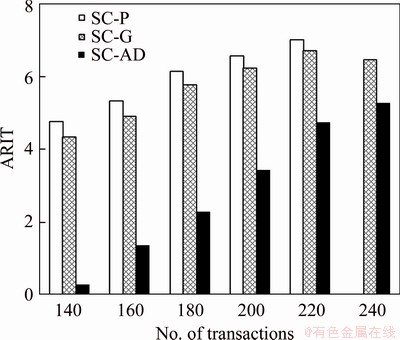
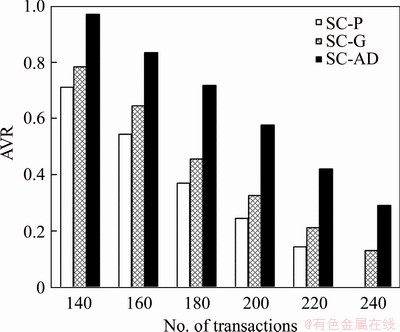
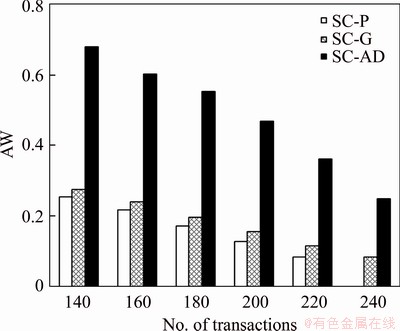
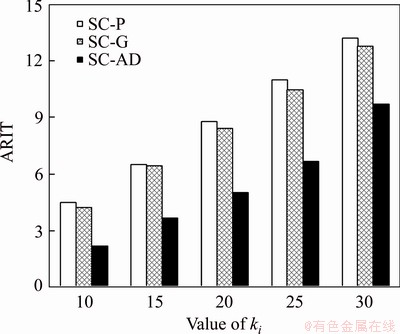
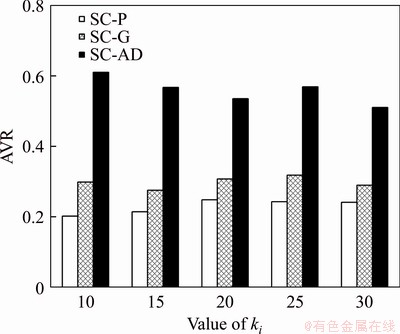
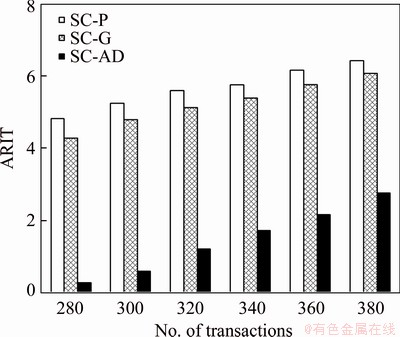
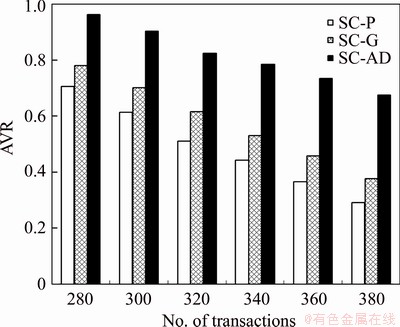
The sensor transactions are scheduled on a multiprocessor platform Π={πi}1≤i≤b. The partitioned approach is considered [24]. That is, a transaction is assigned to a processor and is always executed on it. On each processor, the fixed priority scheduling method is adopted to schedule the transactions. τi ’s priority is larger than τj if i Definition 1: A real-time data object Xi at time tc is temporally consistent if (for its instance τi,j finished last before tc) the sampling time ri,j plus Vi is not less than tc, i.e., ri,j+Vi≥tc [5]. If the temporal consistency of real-time data cannot be fully guaranteed, a promising approach is to skip some transaction instances in a way that the user transactions can access valid data objects in a large part of time. The (m, k)-constrained model is a good choice [25, 26]. In this model, for transaction τi, mi out of any ki consecutive instances’ deadlines must be met. By changing the value of mi, one can obtain different degrees of temporal consistency. There are two major patterns proposed in literature: the evenly-distributed-mandatory pattern and the deeply-red pattern. The former one is used in this paper since it exhibits a relatively good schedulability and stability [26]. According to the evenly-distributed-mandatory pattern, an instance τi,j is accepted if: Otherwise, it can be skipped. For τi, let Pi and Di denote its period and relative deadline, respectively. The total invalid time for ki consecutive instances of τi is (ki–mi)Pi. The relative invalid time of Xi with respect to mi, RIT(Xi,mi), is defined as: The average relative invalid time of the real-time data set X with respect to M={mi}1≤i≤n, ARIT(X, M), is defined as: Then the problem of temporal consistency maintenance on multiprocessor platforms with instance skipping (TCM-IS) is described as follows: Given a sensor transaction set Г scheduled on Π. τi is represented by a three-tuple (Ci, Vi, ki). Determine Pi, Di and mi for each τi, so that ARIT(X, M) is minimized, subject to: 1) For each τi, 3 Partitioned scheduling method In this section, the partitioned scheduling method SC-AD is presented to solve the TCM-IS problem. SC-AD uses HH scheme to assign periods and deadlines to sensor transactions. That is, for each τi, both Pi and Di are set to be Vi/2. 3.1 Determining initial value of M Let λi=Ci/Vi and The following theorem gives a sufficient schedulability condition for Г on Π under any valid partitioning scheme with respect to the given M. Theorem 1: For the given M, Г is schedulable on Π if Proof: Suppose that τi is the first transaction that cannot be assigned to any processor and inequality (3) holds for Г. Let Гk denote the transactions that have been assigned to processor πk. It must be: By taking an upper bound of the left hand side of inequality (4), one has: Summing over all b processors and dividing both sides by Vi/2 yields: From inequality (6), one can obtain: This contradicts inequality (3). So, the theorem is proved. SC-AD uses theorem 1 to determine the initial value of M. It transforms the TCM-IS problem to the following optimization problem: subject to: 1) The number of transactions and the value of ki may be large. Thus the exhaustive searching method could be inefficient. A greedy method is given to solve the above problem. The initial value of each mi is set to 1. Then at each step a transaction is selected to increase its value of mi. Let Ml denote the largest value of mi/ki after l steps. The cost of increasing τi’s value of mi by the step size of δ at the l+1-th step, c(i), is: In Eq. (7), Ii is an indicator function whose value is 1 if (mi+δ)/ki >Ml and 0, otherwise. The utility of τi, u(i), is δ/(2c(i)). In a step, transaction τi is successfully selected if τi has the largest utility and inequality (3) is satisfied after the increase of τi’s value of mi by δ. If no transaction can be selected due to the dissatisfaction of inequality (3) or every transaction’s value of mi reaches the maximum value, the process ends. This process is described in Algorithm 1. Algorithm 1 Calculation of mi Notice that inequality (3) can be evaluated in an incremental way. Let Sl denote the value of the numerator of the right hand side of inequality (3) after l steps. If τi is selected to increase its value of mi, then one just needs to check the following condition: Then Sl+1 is set to Sl+2c(i) if τi has the largest utility and the above condition holds. Thus inequality (3) can be evaluated in constant time and each step takes O(n) time. There are at most 3.2 Partitioning transactions among processors After obtaining the initial value of M, SC-AD assigns the transactions to processors. For τi, define AR (i, t) and FR (i) as follows: To determining whether τi is feasible on πk , the following condition is checked: The time required for the check is O(|Гk|). It’s not hard to see from the proof of theorem 1 that if inequality (8) is satisfied, then τi is feasible on πk. Otherwise, the worst case response time of τi with respect to Гk, Ri,k, is calculated. Notice that Rk (i, t) is non-decreasing with t given mi and Pi, thus Ri,k can be computed in an iterative way. Let Theorem 2: A lower bound of Ri,k , LB(Ri,k ), is Proof: Ri,k is no less than Ci, so we only need to consider the case in which the value of LB(Ri,k) obtained by theorem 2 is larger than Ci. For τi, we show that following condition holds: If 0<>i/2, then: Inequality (10) holds since R(i,t)=Ci in this case.If t>Vi/2, let t=(l+x)Vi/2, l ≥1, 0≤x<1, then: Inequality (10) holds since R(i, t)≥Ci in this case. For a time point t, 0<>i,k), we have: If the inequality condition of theorem 2 holds, by applying inequality (10), we obtain: Thus the theorem is proved. Notice that if the inequality condition of theorem 2 doesn’t hold, then for every time point t, 0<>i/2, it must be: From the proof of theorem 2, we know that τi is certain to be infeasible on πk . LB(Ri,k) can be obtained during the evaluation of inequality (8). Thus there is no extra cost for computing LB(Ri,k). The initial value of Ri,k is set as LB(Ri,k). Ri,k is then computed using Eq. (9) iteratively. The iteration continues until Let λ(k) denote the sum of densities of transactions assigned to πk. SC-AD assigns the transactions to processors in a balanced way. For τi , the processor πkthat is selected to accommodate it is: πk=argmin{λ(l)|τi is feasible on πl, 1≤l≤b}. The processor allocation is described in Algorithm 2. Notice that the transaction set can be successfully allocated among processors under SC-AD if Algorithm 1 succeeds. If Algorithm 1 returns failure, then Algorithm 2 will be invoked for the transaction set with each mi being set to 1. If the partition still fails, the transaction set is considered to be infeasible on Π. The time required for the assignment of τi is O(biVi). The overall time complexity of Algorithm 2 is O(bn2Vmax) where Vmax=max{Vi|1≤i≤n}. Algorithm 2 Processor allocation 3.3 Further reducing ARIT SC-AD tries to further decrease the average relative invalid time by adjusting the values of mi for some transactions. The adjustment starts from the first processor. On each processor, several rounds of adjustment are conducted. In each round, the adjustment is conducted from the transaction with the lowest priority to the transaction with the highest priority. Suppose that transactions on each processor are sorted in decreasing order of their priorities. For simplicity, we reuse τi to denote the i-th transaction on πk. The worst case response time of τi in the lth round, after τs (i>s) is selected for adjustment, is denoted as Ri,k(l,s). When τs is selected, ms is increased by δ, and then Ri,k(l, s) of all τi (i>s) are recalculated. If there is τa with Ra,k(l, s)>Va/2, the adjustment for τs fails, and the next transaction is considered. Theorem 3: If i=s+1, the initial value of Ri,k(l+1,s), Otherwise, max{Ri-1,k(l+1,s)+Ci, Ri,k(l+1,s+1), LB(Ri,k(l+1, s)}. Proof: Let Rl,s(i, t) denote the request bound of τi in [0, t] in the l-th round, after τs’s value of ms is increased. For a time point t, 0≤t<>i,k(l,1): In addition, Rl+1,s(s,t)≥Rl,1(s,t). Thus, Ri,k(l+1, s) is no less than Ri,k(l,1). The initial value of Ri,k(l+1,s) can be set to be Ri,k(l, 1). If i>s+1, then the value of Ri,k(l, 1) is updated when the (s+1)th transaction’s value of ms+1 is increased. With the same reasoning as above, we know that Ri,k(l+1, s) is no less than Ri,k(l+1, s+1). In addition, Ri-1,k(l+1, s) has been derived. For a time point t, 0≤t≤Ri-1,k(l+1, s): Thus Ri,k(l+1, s)≥Ri-1,k(l+1,s)+Ci. From theorem 2 we know that LB(Ri,k(l+1, s)) is also an lower bound of Ri,k(l+1, s). The theorem is proved. Theorem 4: The adjustment for τi on πk is infeasible, if Proof: If the adjustment for τi succeeds, then for each τj (j≠i), mj instances are finished in an interval with length kjVj/2. For τi, mi+δ instances are finished in an interval with length kiVi/2. It must be: This implies: Thus the adjustment for τi fails if the above inequality does not hold. The theorem is proved. The adjustment process is described in Algorithm 3. According to theorem 3, the initial value of Ri,k(l,s) is non-decreasing in l and s. Let O(i) denote τi’s index in Г. The total number of feasibility checks for τi after a higher priority transaction is selected for adjustment is Thus the overall time complexity of Algorithm 3 is Algorithm 3 Adjustment of mi Example 1: Consider a set of transactions {τi}1≤i≤6 scheduled on {πi}1≤i≤2. The parameters of transactions are given in Table 1. The initial values of mi of transactions obtained by SC-AD are {2,1,1,1,2,1}. The transactions are then allocated to processors. Transactions τ1, τ4 and τ5 are assigned to π1, and the rest are assigned to π2. The values of mi of transactions on π1 and π2 are adjusted. For π1, the order of adjustment is τ5, τ4, τ1 in each round. m5 can be set to 6 since it has no impact on other transactions. The values of m4 and m1 can be increased to their maximum values since lower priority transactions remain feasible after adjustment. The similar process is conducted for transactions on π2. The final values of mi of transactions are {6,1,5,3,6,5}. Figure 1 shows the schedule generated by SC-AD in [0,40]. Table 1 Parameters of transactions Figure 1 Schedule generated by SC-AD 4 Performance evaluation In this section, an experimental evaluation of the proposed method was presented. The baseline methods SC-P and SC-G were given for comparison. SC-P uses Algorithm 1 to obtain the values of mi. It then uses First-Fit scheme (FF) to assign the transactions to processors. SC-G determines the values of mi in a greedy way. At each step, transaction τi is selected to increase mi by δ if τi has the largest value of ((mi+δ)ci/kiVi) and the transaction set Г is feasible after this increase. The feasibility of Г is determined by trying to partition the transactions among the processors. Inequality (8) is used to determine whether a transaction can be accommodated to a processor. The performance metrics include the average relative invalid time (ARIT), the average valid ratio(AVR) and the average workload (AW). ARIT is given by Eq. (2). Let T denote the simulation time, L(i), the total valid time of Xi during T, then: Let W(i) denote the total busy time of processor πi during T, then: A summary of the parameters and default settings used in experiments are presented in Table 2. Systems with two and four processors were studied. The validity interval of a real-time data object is uniformly distributed between 2000 and 4000 ms. The computation time of a sensor transaction is uniformly distributed between 10 and 20 ms. The value of parameter ki is randomly selected in Refs. [10, 20]. Table 2 Parameters and settings Figure 2 shows the average relative invalid time of the methods when the number of sensor transactions varies from 140 to 240. The number of processors is 2. It can be seen that the ARIT of SC-AD is constantly lower than that of SC-P or SC-G. For example, when the number of transactions is 180, the ARIT of SC-AD is about 2.29, while the ARIT of SC-P and SC-G is about 6.13 and 5.77, respectively. This is because after assigning the transactions to processors, SC-AD adjusts the values of mi for transactions on each processor according to the worst case response times of them. This further decreases the ARIT. As the number of transactions increases, the processor resources left for the methods to increase the values of mi become less, thus the ARIT of the methods increases and the difference between them decreases. This is also verified in Figure 2. When the number of transactions reaches 240, SC-P always returns failure, and thus its ARIT becomes zero. However, SC-AD and SC-G can still provide certain degree of consistency. At this time, the ARIT of SC-AD is still lower than that of SC-G. Figure 2 Average relative invalid time comparison (b=2) Figure 3 shows the average valid ratio of the methods. It can be seen that the AVR of SC-AD is always higher than that of SC-P or SC-G. This is because according to Figure 2, the average value of mi under SC-AD is larger than that under the other two methods. This means that more instances will be finished under SC-AD. If instance τi,j is finished at fi,j, the data object Xi will be valid in [fi,j, ri,j +Vi]. Thus on the average the total valid time of a data object under SC-AD is larger than that under SC-P and SC-G. With the increase of transaction set size, the mi becomes smaller; therefore, all methods’ AVR decrease. Figure 4 shows the average workload of the methods. Since the average value of mi under SC-AD is larger than that under SC-P or SC-G, the AW of SC-AD is also higher than that of SC-P or SC-G. This is verified by Figure 4. For example, when the transaction set size is 140, the AW of SC-AD is about 0.68 while the AW of SC-P and SC-G is about 0.25 and 0.27, respectively. All methods’ AW decrease with the increase of transaction set size. Figure 3 Average valid ratio comparison (b=2) Figure 4 Average workload comparison (b=2) Figure 5 shows the average relative invalid time of the methods under different values of ki. The number of transactions is fixed at 200. It can be seen that the ARIT of SC-AD is always lower than that of SC-P or SC-G. In addition, with the increase in the value of ki, all methods’ ARIT increase. The reason is that under different values of ki, the average system workloads are very similar due to the fixed number of transactions. This means that the resources left for a method to increase mi are also nearly the same. Therefore, a larger ki leads to a larger value of ARIT. Figure 6 shows the average valid ratio of the methods. It can be seen that the AVR of SC-AD is higher than that of SC-P or SC-G. According to Figure 5, the average ratios between mi and ki of a method are very similar under different ki, and thus the differences of AVRs under each method are not larger. This is also verified in Figure 6. Figure 5 Average relative invalid time comparison (b=2, n=200) Figure 6 Average valid ratio comparison (b=2, n=200) Figures 7 and 8 show the average relative invalid time and the average valid ratio of the methods when the number of sensor transactions varies from 280 to 380. The number of processors is 4. It can be seen that the ARIT of SC-AD is still lower than that of SC-P or SC-G, and the AVR of SC-AD is larger than that of SC-P or SC-G. Experiments were also repeated for 8 processors; similar results were observed and are omitted here for brevity. Figure 7 Average relative invalid time comparison (b=4) Figure 8 Average valid ratio comparison (b=4) 5 Conclusions In this paper, the problem of maintaining temporal consistency of real-time data on multiprocessor platforms with instance skipping was studied. This problem was formulated based on the (m,k)-constrained model. A partitioned scheduling method SC-AD was proposed. SC-AD judiciously determines the value of m for each transaction and allocates transactions among processors. It further increases the values of m for transactions on each processor. It is demonstrated through experiments that compared with the baseline methods, SC-AD archives lower average relative invalid time and higher average valid ratio. Contributors BAI Tian provided the method and wrote the first draft of the manuscript; LI Zhi-jie conducted the literature review and edited the draft of manuscript; FAN Bo analyzed the experimental results and edited the draft of manuscript. Conflict of interest BAI Tian, LI Zhi-jie, and FAN Bo declare that they have no conflict of interest. References [1] CINTUGLU M H, MOHAMMED O A, AKKAYA K, ULUAGAC A S. A survey on smart grid cyber physical system testbeds [J]. IEEE Communications Surveys & Tutorials, 2017, 19(1): 446-464. DOI: 10.1109/COMST. 2016.2627399. [2] CANIZO M, CONDE A, CHARRAMENDIETA S, MINON R, CID-FUENTES R G, ONIEVA E. Implementation of a large-scale platform for cyber-physical system real-time monitoring [J]. IEEE Access, 2019, 7: 52455-52466. DOI: 10.1109/ACCESS.2019. 2911979. [3] CAI X. Collaborative prediction for bus arrival time based on CPS [J]. Journal of Central South University, 2014, 21(3): 1242-1248. DOI: 10.1007/s11771-014-2058-5. [4] XIONG M, RAMAMRITHAM K. Deriving deadlines and periods for real-time update transactions [J]. IEEE Transactions on Computers, 2004, 53(5): 567-583. DOI: 10.1109/TC.2004.1275297. [5] XIONG M, HAN S, LAM K Y, CHEN D. Deferrable scheduling for maintaining real-time data freshness: Algorithms, analysis, and results [J]. IEEE Transactions on Computers, 2008, 57(7): 952-964. DOI: 10.1109/ TC.2008. 16. [6] HAN S, CHEN D J, XIONG M, LAM K Y, MOK A K, RAMAMRITHAM K. Schedulability analysis of deferrable scheduling algorithms for maintaining real-time data freshness [J]. IEEE Transactions on Computers, 2014, 63(4): 979-994. DOI: 10.1109/TC.2012.266. [7] XIONG M, WANG Q, RAMAMRITHAM K. On earliest deadline first scheduling for temporal consistency maintenance [J]. Real-Time Systems, 2008, 40(2): 208-237. DOI: 10.1007/s11241-008-9055-4. [8] LI J J, XIONG M, LEE V C S, SHU L C, LI G. Workload-efficient deadline and period assignment for maintaining temporal consistency under EDF [J]. IEEE Transactions on Computers, 2013, 62(6): 1255-1268. DOI: 10.1109/TC.2012.69. [9] HAN S, LAM K Y, CHEN D, XIONG M, WANG J, RAMAMRITHAM K, MOK A K. Online mode switch algorithms for maintaining data freshness in dynamic cyber-physical systems [J]. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(3): 756-769. DOI: 10.1109/TKDE.2015.2496199. [10] LI J, CHEN J, XIONG M, LI G, WEI W. Temporal consistency maintenance upon partitioned multiprocessor platforms [J]. IEEE Transactions on Computers, 2016, 65(5): 1632-1645. DOI: 10.1109/TC.2015.2448088. [11] ZHOU C, LI G, LI J, GUO B. Energy-aware real-time data processing for IoT systems [J]. IEEE Access, 2019, 7: 171776-171789. DOI: 10.1109/ACCESS.2019.2956061. [12] DENG C, LI G, ZHOU Q, LI J. Co-scheduling of hybrid transactions on multiprocessor real-time database systems [J]. IEEE Access, 2019, 7: 109506-109517. DOI: 10.1109/ ACCESS.2019.2932799. [13] KANG K D. Enhancing timeliness and saving power in real-time databases [J]. Real-Time Systems, 2018, 54: 484-513. DOI: 10.1007/s11241-018-9302-2. [14] KANG K D, SON S H, STANKOVIC J A. Managing deadline miss ratio and sensor data freshness in real-time databases [J]. IEEE Transactions on Knowledge and Data Engineering, 2004, 16(7): 1200-1216. DOI: 10.1109/TKDE. 2004.61. [15] AMIRIJOO M, HANSSON J, SON S H. Specification and management of QoS in real-time databases supporting imprecise computations [J]. IEEE Transactions on Computers, 2006, 55(3): 304-319. DOI: 10.1109/TC.2006. 45. [16] ZHOU Y, KANG K D. Deadline assignment and feedback control for differentiated real-time data services [J]. IEEE Transactions on Knowledge and Data Engineering, 2015, 27(12): 3245-3257. DOI: 10.1109/TKDE.2015.2441725. [17] KANG W, SON S H, STANKOVIC J A. Design, implementation, and evaluation of a QoS-aware real-time embedded database [J]. IEEE Transactions on Computers, 2012, 61(1): 45-59. DOI: 10.1109/TC.2010.240. [18] AMIRIJOO M, CHAUFETTE N, HANSSON J, SON S H, GUNNARSSON S. Generalized performance management of multi-class real-time imprecise data services [C]// 26th IEEE International Real-Time Systems Symposium. Miami, FL, USA, 2005: 38-49. DOI: 10.1109/RTSS.2005.23. [19] XIONG M, LIANG B, LAM K Y, GUO Y. Quality of service guarantee for temporal consistency of real-time transactions [J]. IEEE Knowledge and Data Engineering, 2006, 18(8): 1097-1110. DOI: 10.1109/TKDE.2006.128. [20] WANG J, LAM K Y, HAN S, SON S H, MOK A K. An effective fixed priority co-scheduling algorithm for periodic update and application transactions [J]. Computing, 2013, 95(10, 11): 993-1018. DOI: 10.1007/s00607-012-0242-8. [21] HAN S, LAM K Y, WANG J, SON S H, MOK A K. Adaptive co-scheduling for periodic application and update transactions in real-time database systems [J]. Journal of Systems and Software, 2012, 85(8): 1729-1743. DOI: 10.1016/j.jss.2012.03.055. [22] HAN S, LAM K Y, WANG J T, RAMAMRITHAM K, MOK A K. On co-scheduling of update and control transactions in real-time sensing and control systems: Algorithms, analysis, and performance [J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(10): 2325-2342. DOI: 10.1109/ TKDE.2012.173. [23] KANG K D. Reducing deadline misses and power consumption in real-time databases [C]// IEEE Real-Time Systems Symposium. Porto, Portugal, 2016: 257-268. DOI: 10.1109/RTSS.2016.033. [24] ROBERT I D, ALAN B. A survey of hard real-time scheduling for multiprocessor systems [J]. ACM Computing Surveys, 2011, 43(4): 1-44. DOI: 10.1145/1978802. 1978814. [25] WEST R, POELLABAUER C. Analysis of a window constrained scheduler for real-time and best-effort packet streams [C]// IEEE Real-Time Systems Symposium. Orlando, FL, USA, 2000: 239-248. DOI: 10.1109/REAL.2000. 896013. [26] RAMANATHAN P. Overload management in real-time control applications using (m,k)-firm guarantee [J]. IEEE Transactions on Parallel and Distributed Systems, 1999, 10(6): 549-559. DOI: 10.1109/FTCS.1997.614086. (Edited by YANG Hua) 中文导读 多处理器平台上考虑实例丢弃的数据时态一致性维护 摘要:维护实时数据的时态一致性对于信息物理融合系统来说非常重要。已有的研究工作大多针对单处理器平台来进行。基于(m, k)约束模型定义了多处理器平台上考虑实例丢弃的时态一致性维护问题,提出了一种解决该问题的方法SC-AD。SC-AD利用推导出的传感器事务集可调度的充分条件来确定各传感器事务参数m的初始值,然后据此进行多处理器事务分派。SC-AD合理地增加各处理器上已分派事务参数m的值以进一步降低实时数据的平均相对无效时间。实验结果表明,在不同的系统负载下,SC-AD在平均相对无效时间和平均有效率等性能指标上都要优于基线算法。 关键词:信息物理融合系统;传感器事务;多处理器调度;时态一致性 Foundation item: Project(2020JJ4032) supported by the Hunan Provincial Natural Science Foundation of China Received date: 2020-03-18; Accepted date: 2020-08-06 Corresponding author: BAI Tian, PhD, Lecturer; Tel: +86-18390188018; E-mail: baitiannobel@163.com; ORCID: https://orcid.org/ 0000-0003-0540-5472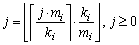
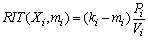 (1)
(1)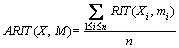 (2)
(2)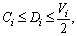
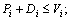 2) For each τi,
2) For each τi, 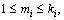
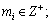 and 3) For each πi, the set of transactions assigned to πi is feasible under the fixed priority scheduling.
and 3) For each πi, the set of transactions assigned to πi is feasible under the fixed priority scheduling.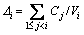 denote the density and the cumulative density of τi, respectively. Let λmax=max{λi|1≤i≤n} and Δmax=max{Δi|1≤i≤n} denote the maximum density and maximum cumulative density among transactions in Г, respectively. According to Ref. [26], the request bound of τi in [0, t], R (i,t), is:
denote the density and the cumulative density of τi, respectively. Let λmax=max{λi|1≤i≤n} and Δmax=max{Δi|1≤i≤n} denote the maximum density and maximum cumulative density among transactions in Г, respectively. According to Ref. [26], the request bound of τi in [0, t], R (i,t), is: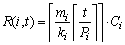
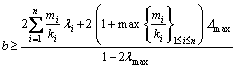 (3)
(3)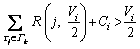 (4)
(4)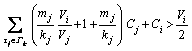 (5)
(5)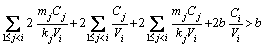 (6)
(6)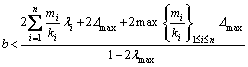
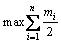
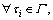
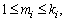
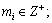 and 2) Inequality (3) is satisfied.
and 2) Inequality (3) is satisfied.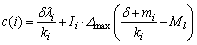 (7)
(7)
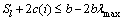
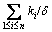 steps. Therefore, the overall time complexity of Algorithm 1 is
steps. Therefore, the overall time complexity of Algorithm 1 is 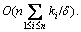
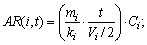
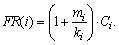
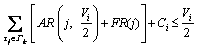 (8)
(8)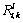 denote the value of Ri,k after the l-th iteration. Then:
denote the value of Ri,k after the l-th iteration. Then: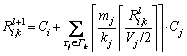 (9)
(9)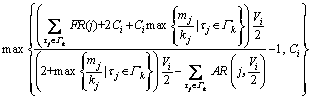 if
if 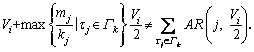
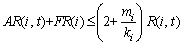 (10)
(10)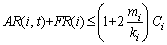 .
.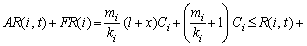
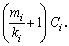
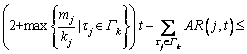
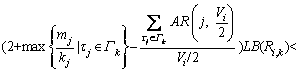
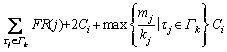 .
.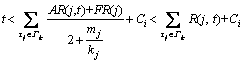 .
.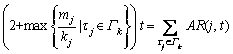 .
.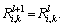 If
If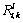 ≤Vi/2 at this time, then τi is feasible on πk. If there is one value of Ri,k that is larger than Vi/2 during the iteration, τi is considered to be infeasible on πk . The computation of Ri,k takes O(|Гk|Vi) time.
≤Vi/2 at this time, then τi is feasible on πk. If there is one value of Ri,k that is larger than Vi/2 during the iteration, τi is considered to be infeasible on πk . The computation of Ri,k takes O(|Гk|Vi) time.
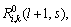 can be set to be:
can be set to be: 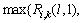
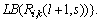
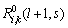 can be set to be:
can be set to be: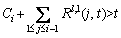 .
.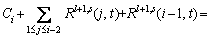
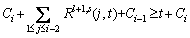
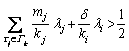 (11)
(11)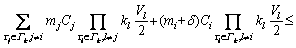
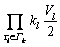 .
.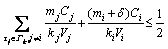 .
.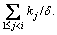 The total time required for the checks is
The total time required for the checks is 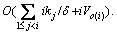 If the adjustment for τs fails and τa(a>s) is the first transaction with Ra,k(l,s)>Va/2, and then for each τi (so(i)) must be added. Let SF(k) denote the set of transactions on πk that need to take the extra time into account. The time required for the adjustment of values of mi is calculated as follows:
If the adjustment for τs fails and τa(a>s) is the first transaction with Ra,k(l,s)>Va/2, and then for each τi (so(i)) must be added. Let SF(k) denote the set of transactions on πk that need to take the extra time into account. The time required for the adjustment of values of mi is calculated as follows: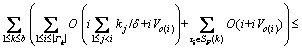
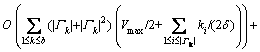
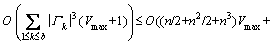
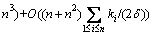 .
.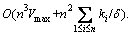
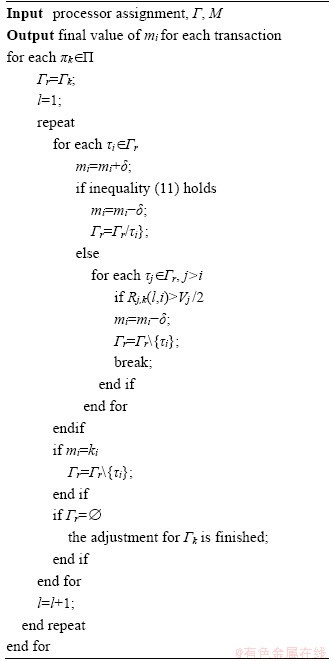
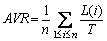 .
.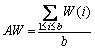 .
.
Abstract: Maintaining temporal consistency of real-time data is important for cyber-physical systems. Most of the previous studies focus on uniprocessor systems. In this paper, the problem of temporal consistency maintenance on multiprocessor platforms with instance skipping was formulated based on the (m,k)-constrained model. A partitioned scheduling method SC-AD was proposed to solve the problem. SC-AD uses a derived sufficient schedulability condition to calculate the initial value of m for each sensor transaction. It then partitions the transactions among the processors in a balanced way. To further reduce the average relative invalid time of real-time data, SC-AD judiciously increases the values of m for transactions assigned to each processor. Experiment results show that SC-AD outperforms the baseline methods in terms of the average relative invalid time and the average valid ratio under different system workloads.


