J. Cent. South Univ. Technol. (2007)05-0719-06
DOI: 10.1007/s11771-007-0137-6 
Damage constitutive model for strain-softening rock based on
normal distribution and its parameter determination
CAO Wen-gui(曹文贵), LI Xiang(李 翔), ZHAO Heng(赵 衡)
(Institute of Geotechnical Engineering, Hunan University, Changsha 410082, China)
Abstract：Firstly, using the damage model for rock based on Lemaitre hypothesis about strain equivalence, a new technique for measuring strength of rock micro-cells by adopting the Mohr-Coulomb criterion was developed, and a statistical damage evolution equation was established based on the property that strength of micro-cells is consistent with normal distribution function, through discussing the characteristics of random distributions for strength of micro-cells, then a statistical damage constitutive model that can simulate the full process of rock strain softening under specific confining pressure was set up. Secondly, a new method to determine the model parameters which can be applied to the situations under different confining pressures was proposed, by deeply studying the relations between the model parameters and characteristic parameters of the full stress-strain curve under different confining pressures. Therefore, a unified statistical damage constitutive model for rock softening which can reflect the effect of different confining pressures was set up. This model makes the physical property of model parameters explicit, contains only conventional mechanical parameters, and leads its application more convenient. Finally, the rationality of this model and its parameters-determining method were identified via comparative analyses between theoretical and experimental curves.
Key words:
constitutive model; rock; damage; strain softening; normal distribution ；
1 Introduction
In recent years, some researches on simulating the full process of strain softening of deformation and failure for rock have been made some progress by introducing the statistical damage theory, and its basic idea[1-2] is: firstly, a damage model was proposed by using Lemaitre hypothesis of strain equivalence, and then a strain-softening damage evolution equation was developed according to random distribution of failure for rock micro-cells, consequently, a statistical damage constitutive model simulating the full process of rock deformation was set up. It can reflect the characteristic of strain softening under specific confining pressure to some extent, however, there is a great gap between theoretical and practical curve (σ1-ε1 curve), in particular under different confining pressure conditions. The reason lies in the fact that the rationality of measuring method for micro-cell strength, its form of random distribution function, and the method in determining the model parameters is subject to restrictions.
Firstly, concerning the reasonable measuring method of micro-cell strength, it was measured by the axial strain of rock sample by TANG[3]. Although this method can reflect the bearing capability of micro-cells to some extent, it is still deficient since the bearing capability of micro-cells is directly related to the stress state occurring on rock specimen. Therefore, CAO et al[4] proposed the measuring method of micro-cell strength F for the first time based on the Drucker-Prager strength criterion, which worked well in practice. Nevertheless, as we all know, the Drucker-Prager strength criterion is conservative, consequently, a more reasonable form of strength criterion should be adopted. Secondly, with respect to random distribution function of micro-cell strength, a statistical damage evolution model for rock softening was developed by KRAJCINOVIC et al[1-2], TANG[3] and CAO et al[4] based on the characteristic that strength of micro-cells accords with the Weibull distribution function, which led to a new path for the research on damage evolution model. However, the Weibull distribution function can only reflect the stochastic situations of micro-cell strength at the interval [0, + ∞]. Actually, the value of strength of micro-cells should be gained at the interval (-∞，+∞), accordingly, the certain irrationality still exists in this method based on the Weibull distribution, and a more reasonable form of random distribution function should be used to describe the stochastic distribution. Thirdly, in regard to the approach on determining parameters of statistical damage constitutive model, the model parameters were mostly determined with regression for the stress-strain curve by rock tri-axial test in the past. Obviously, some deficiencies exist in this method. On the one hand, it makes the constitutive model only reflect the process of strain-softening under specific confining pressure, on the other hand, it gets the physical meaning of model parameters unclear, and makes the number of model parameters increase. Therefore, CAO et al[5] proposed a new method for determining the parameters through discussing experiential relationship between the model parameters and confining pressure, which can reflect the situations under different confining pressures to some extent. However, for different types of rock, the relationship between the model parameters and confining pressure by regression is extremely complicated and uncertain, so the adjustability of this method is subject to considerable restrictions. Although YANG et al[6] improved the method by discussing the relationship between the model parameters and characteristic parameters (stress and strain at peak point) in the stress-strain curve, the model determined by this method can still only be applied to simulate the strain-softening process under specific confining pressure.
Taken together, in order to establish the statistical damage constitutive model reflecting the full process of strain softening for rock, the research work must be carried out comprehensively by deeply exploring the measuring method of strength of micro-cells, its form of random distribution function, and the approach on determining model parameters. It is just the core content of this paper.
2 Establishment of statistical damage softening constitutive model for rock
According to Lemaitre hypothesis of strain equivalence, the damage model for rock can be established as follows [7-8]：
(1)
where [c] is the elastic matrix, [σ] is the nominal stress matrix, [σ*] is the effective stress matrix, and [ε] is the strain matrix, D is the damage variable. Thus, it is concluded that determination of damage variable D is a key for establishment of damage constitutive model.
As rock is the non-homogeneous geological material and contains a great deal of random fissures and voids, the failure of micro-cells under external loads appears to be random. If the distribution density of probability of failure for micro-cells with strength F is assumed as P(x), the rock damage variable D can be defined as
(2)
As the factors affecting failure of micro-cells are complex, which are related not only to the axial strain in tri-axial test, but also to the stress state occurring on rock specimen[9-10]. Therefore, parameter that can be used to measure strength of micro-cells is critical for determination of damage variable. In the past, strength of micro-cells was measured mainly by axial strain[3], however, the authors for this paper think that there are many drawbacks since the effect of complicated stress state on micro-cell strength is not fully reflected by axial strain. Then, a new measuring method for strength F based on the Drucker-Prager strength criterion was proposed firstly in the previously published journal[4]. However, as the Drucker-Prager strength criterion is conservative, the reasonableness and accuracy of this method are subject to many restrictions, and a more reasonable strength criterion of failure for micro-cells must be adopted. As the Mohr-Coulomb strength criterion was established based on the test and can reflect strength of rock more accurately, the measuring method of micro-cell strength established by the Mohr-Coulomb criterion will be more reasonable, and be in good agreement with practical situations.
The Mohr-Coulomb strength criterion expressed with major stresses can be described as
(3)
where c is the cohesive force, φ is the inner friction angle. Here, F=f(σ*) can reflect the risky degree of yielding and failure of micro-cells and can measure micro-cell strength more accurately. However, 
and
in Eqn.(3) are the actual microscopic stress (effective stress) for unbroken rock materials, they can not be directly measured through rock mechanics test. Therefore, the relationship between effective stress and measurable macroscopic variable (σi and εi, =1, 2, 3) must be established. Thus, the method for determining strength of micro-cells by adopting measurable macroscopic variable will be discussed below.
The nominal major stresses σ1, σ2 , σ3 and the major strain ε1 can be measured by tri-axial test, thus, just the corresponding effective stresses
,
,
can be determined by the Hooke’s law and Eqn.(1), their expressions can be obtained as follows:
(4)
i=1, 2, 3 (5)
Substituting Eqns.(4) and (5) into Eqn.(3), strength of micro-cells expressed with measurable macroscopic variable can be described as
(6)
where E and μ are the elastic modulus and the Poisson ratio, respectively.
In addition, it is known from Eqn.(2) that the probability of failure of micro-cells must be determined in order to establish the statistical damage evolution equation. Thus, TANG[3] and CAO et al[4] took another new approach to set up a new method for calculating the probability of failure of micro-cells based on the assumption that micro-cell strength is in agreement with the Weibull distribution. Nevertheless, the Weibull distribution can only reflect the distribution of micro-cell strength at the interval [0, + ∞), and it is obvious that the values of micro-cell strength, which are determined by Eqn.(3) or Eqn.(6) should be at the interval (-∞，+∞), thereby, the above computational method is unreasonable. If the method in describing the random distribution of micro-cell strength with normal distribution function is adopted, the aforementioned deficiency will be overcome. Therefore, a method in calculating the probability of distribution for strength of micro-cells with normal distribution function will be proposed.
The function of probability density that describes the failure of micro-cells can be expressed as follows:
(7)
where S0 and F0 are parameters of normal distribution function for strength of micro-cells and can reflect the mechanical property of rock materials. Thus, substituting Eqn.(7) into Eqn.(2), the probability of failure of micro-cells or damage variable D, which is also called as the statistical damage evolution equation, can be shown as
dx (8)
According to mathematical concept of normal distribution function, Eqn.(8) can be also rewritten approximately as
(9)
In order to develop the damage constitutive model, substituting Eqn.(9) into Eqn.(1). Hereby, the statistical damage constitutive model simulating the full process of axial deformation of rock under tri-axial test can be shown as follows:
(10)
It is known from the above that a key problem for establishment of strain-softening statistical damage constitutive model is the determination of model parameters S0 and F0. The specific method will be introduced in details below.
3 Determination of parameters of statistical damage constitutive model for rock
At present, many scholars have put forth a variety of methods for determining parameters of statistical damage constitutive model for rock, however, these methods, just aforementioned, all have some deficiency or localizability. The ideal method for determining parameters of statistical damage constitutive model must not only be applied to the complex situations under different confining pressures, but also make the physical meaning of model parameters much more clear, and does not increase unconventional parameters of rock mechanics, thereby, a new approach must be taken to set up a method for determining parameters of this model.
To determine parameters
and
of statistical damage softening constitutive model, the following two steps must be carried out: firstly, according to the extremity characteristic in the full strain-stress curve of softening deformation process, the relationship between model parameters and characteristic parameters (stress at the peak point and its corresponding strain) under specific confining pressure should be set up. Secondly, the relations between stress at the peak point and different confining pressures will be developed by introducing the Mohr-Coulomb strength criterion, and the formula with general significance of the relations between corresponding strain and different confining pressures then will be deduced. Accordingly, the relationship between model parameters and conventional parameters of rock mechanics (such as the elastic modulus, Poisson ratio, cohesive force and inner friction angle) under different confining pressures can be developed.
3.1 Determination of model parameters under specific confining pressure
As the extremity of stress-strain curve simulating the full process of deformation under special confining pressures must be gained, the following equation can be obtained through the derivative action of σ1 on ε1 by way of Eqn.(10), if both σf and εf are assumed as the peak values in the σ1-ε1 curve, and at this peak point, its corresponding strength of micro-cells and damage variable are Ff and Df respectively, then
dσ1/dε1=0 (11)
as σf and εf satisfy Eqn.(10), Eqn.(10) can be rewritten as
(12)
moreover, the following equation can also be obtained according to Eqns. (4), (5) and (10):
(13)
thus, if Eqn.(8) is combined with Eqn. (13), the damage variable D can be expressed as follows:
(14)
where 
is the standard function of normal distribution. Then Df can be also expressed as
(15)
where Ff can be deduced from Eqn. (6), it is shown as
(16)
using Eqns. (12), (15) and (16), Eqn. (11) can also be rewritten as
(17)
it is worth noting that if Z is supposed as the value of (Ff-F0)/S0 in Eqn. (15), it can be identified by the value of σf and εf according to the table of standard normal distribution function, that is
(18)
then, combine Eqn.(15) with Eqn.(17), parameter S0 can be determined as follows:
(19)
henceforth, parameter F0 can also be obtained by Eqn.(18):
(20)
accordingly, the formula of parameters S0 and F0 of strain-softening statistical damage constitutive model under specific confining pressure is deduced.
3.2 Determination of parameters of unified model under different confining pressures
The above introduced method for determining parameters of statistical damage constitutive model for rock is mainly restricted to specific confining pressure. However, due to the inclusion of parameters σf and εf in the computational formula of parameters S0 and F0, the determination of σf and εf becomes a critical problem to calculate the model parameters S0 and F0. However, σf and εf are difficultly gained by rock mechanics test, therefore, the relationship between characteristic parameters (σf and εf) and conventional parameters (such as the cohesive force c, inner friction angle φ) should be established, that is the method to determine σf and εf.
3.2.1 Method of determining stress at peak point
As the axial stress σf at the peak point represents the tri-axial compressive strength under different confining pressures, σf satisfies the Mohr-Coulomb strength criterion:
(21)
thus, the formula of σf and σ3 can be readily set up.
3.2.2 Method of determining strain at peak point
The procedure of determination of parameter εf can be carried out by analyzing the relationship between εf and confining pressure σ3. Therefore, the analysis is carried out according to large types of experimental data of rocks, and its results in Table 1 show a good and universal linear relation to confining pressure σ3, the correlation coefficient of linear regression is all greater than 0.98. Hence, parameter εf can be expressed as a linear algebraic equation of confining pressure σ3, that is
(22)
where parameters a and b are constants that can be obtained by linear regression according to the data of tri-axial test. Hereby, the calculating method of εf can be established.
Table 1 Regression results of strain at peak point vs confining pressure for different rocks
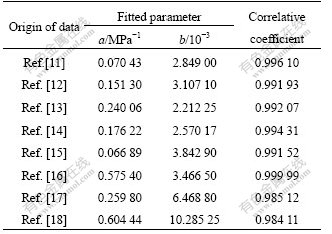
It can be seen that strain εf at the peak point presents a universal simple linear relation to corresponding confining pressure σ3. Thus, adopting this method to the calculate εf can avoid the uncertainty of parameters- determining method, and it not only strengthens the operation, but is convenient to engineering application.
4 Application and verification
One practical example is introduced in order to verify the rationality of strain-softening statistical damage constitutive model for rock and its method to determine model parameters. In this example, by introducing the published data[12] , some mechanical parameters such as the elastic modulus E, the Poisson ratio μ, the inner friction angle φ and cohesive force c as well as parameters a and b were obtained, they are 51.62 GPa, 0.25, 44.014?，27.962 MPa, 0.151 3 MPa-1 and 3.107 10×10-3, respectively. The theoretical stress- strain curves under different confining pressure by the model were then obtained, and a comparison between the theoretical curves and experimental curves was performed[12]. The results are shown in Fig.1. It is seen from Fig.1 that the unified model proposed in this paper can reflect the full process of deformation and failure for rock in complicated stress conditions, especially the property of its strain softening and the changing characteristics of strength when confining pressure changes. Therefore, theoretical results from the model meet the computational requirements for practical engineering.
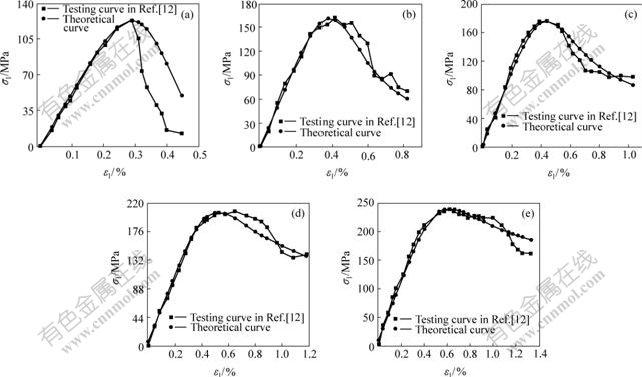
Fig.1 Comparison between experimental and theoretical curves at different confining pressures
(a) σ3=0; (b)σ3=3.5 MPa; (c)σ3=7.0 MPa; (d)σ3=14.0 MPa; (e)σ3=21.0 MPa
5 Conclusions
1) The measuring method of micro-cell strength based on the Mohr-Coulomb strength criterion can better describe the bearing capability of micro-cells, and accords better with practice than that of the previously proposed.
2) Describing the distribution of strength of micro- cells by adopting normal distribution function can avoid irrationality of gain-value interval of strength of micro-cells led by the Weibull distribution.
3) The method in determining parameters of statistical damage constitutive model can make the physical meaning of model parameters more explicit, eliminate its uncertainty, and enhance its reliability, thus it has a strong universal applicability.
4) The unified strain-softening statistical damage constitutive model proposed in this paper contains only conventional parameters of rock mechanics (such as the elastic modulus E, the Poisson ratio μ, inner friction angle φ and cohesive force c, confining pressure σ3), and does not add more unconventional parameters. As a result, it is more convenient to application.
References
[1] KRAJCINOVIC D, FONSEKA, G U. The continuous damage theory of brittle materials (Part I, II)[J]. Journal of Applied Mechanics, 1981, 48: 809-824.
[2] KRAJCINOVIC D, SILVA M A G. Statistical aspects of the continuous damage theory[J]. Int J Solids Structures, 1982, 18(7): 551-562.
[3] TANG Chun-an. Catastrophe in Rock Unstable Failure[M]. Beijing: The Coal Industry Publication Company, 1993. (in Chinese)
[4] CAO Wen-gui, FANG Zu-lie, TANG Xue-jun. A study of statistical constitutive model for softening and damage rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(6): 628-633. (in Chinese)
[5] CAO Wen-gui, ZHAO Ming-hua, LIU Cheng-xue. Study on the model and its modifying method for rock softening and damage based on Weibull random distribution[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3223-3231. (in Chinese)
[6] YANG Ming-hui, ZHAO Ming-hua, CAO Wen-gui. Method for determining the parameters of statistical damage softening constitutive model for rock[J]. Journal of Hydraulic Engineering, 2005, 36(3): 345-349. (in Chinese)
[7] LEMAITRE J. How to use damage mechanics[J]. Nuclear Engineering and Design, 1984, 80(3): 233-245.
[8] LEMAITRE J. A continuous damage mechanics model for ductile fracture[J]. Journal of Engineering Materials and Technology, 1985, 107(1): 83－89.
[9] PAN Chang-liang, ZHU Fang-cai, CAO Ping, et al. Characteristics of acoustic emission of bursting-intended rocks under uniaxial compression[J]. Journal of Central South University of Technology: Natural Science, 2001, 32(4): 336-338. (in Chinese)
[10] HU Liu-qing, LI Xi-bing. Damage and fragmentation of rock under experiencing impact load[J]. Journal of Central South University of Technology, 2006, 13(4): 432-437.
[11] ZHOU Wei-yuan, WU-Peng, YANG Ruo-qiong. The Damage Model of Rock[M]. Shenyang: Northeast College of Engineering, 1989: 37-53. (in Chinese)
[12] KAWAMOTO T. Deformation and fracturing behavior of discontinuous rock mass and damage mechanics theory[J]. Int J Num Anal Methods Geomech, 1988, 12: 1-30.
[13] ZENG Ya-wu, ZHAO Zhen-ying, ZHU Yi-wen. Bifurcation analysis on failure forms of rock material[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(7): 948-952. (in Chinese)
[14] LIN Zhuo-ying, WU Yu-shan, GUAN Lin-li. Research on the brittle-ductile transition property of rocks under triaxial compression[J]. Rock and Soil Mechanics, 1992, 13(2/3): 45-51. (in Chinese)
[15] YE Jin-han. The stress-strain curve and testing techniques of rock[J]. Journal of Hydraulic Engineering, 1984(9): 43-48. (in Chinese)
[16] LU Yun-de, GE Xiu-run, JIANG Yu, et al. Study on conventional triaxial compression test of complete process for marble and its constitutive equation[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(15): 2489-2493. (in Chinese)
[17] YOU Ming-qin. Effect of confining pressure on the Young’s modulus of rock specimen[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(1): 53-60. (in Chinese)
[18] SU Cheng-dong, ZHAI Xin-xian, LI Yong-ming, et al. Study on deformation and strength of coal samples in triaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S1): 2963-2968. (in Chinese)
Foundation item: Project (50378036) supported by the National Natural Science Foundation of China; Project (03JJY5024) supported by the Natural Science Foundation of Hunan Province, China
Received date: 2007-03-22; Accepted date: 2007-05-23
Corresponding author: CAO Wen-gui, Professor, PhD; Tel: +86-731-8821659; E-mail：cwglyp@public.cs.hn.cn
(Edited by YANG Hua)
