J. Cent. South Univ. (2017) 24: 2288-2293

DOI: https://doi.org/10.1007/s11771-017-3640-4

Electronic structure and flotability of gold-bearing pyrite: A density functional theory study

LIU Dan(刘丹), WANG Yi-jie(王伊杰), XIAN Yong-jun(先永骏), WEN Shu-ming(文书明)

State Key Laboratory of Complex Nonferrous Metal Resources Clean Utilization(Kunming University of Science and Technology), Kunming 650093, China

Central South University Press and Springer-Verlag GmbH Germany 2017

Abstract:

Various incorporation of Au in pyrite and its effects on the geometrical structure, electronic structure and flotability of pyrite were theoretically investigated and fully discussed by performing density functional theory (DFT). The calculated incorporation energy shows that gold would most likely exist in pyrite via incorporating into interstitial lattice sites in the absence of As impurity. As a result of incorporated Au, the covalence levels of the S—Fe and S—S bonds are changed, and the tonicity of Au—S bonds and antibonding of Au—Fe bonds are found to form in the pyrite, which would change the natural flotability of pyrite. The Au impurity energy levels are introduced into the energy band and result in the transformation of pyrite semiconductivity type. The calculated band-gap value suggests that the incorporated Au significantly decreases pyrite semiconductivity level, which enhances the formation and the adsorption stability of dixanthogen during pyrite flotation. The DOS results reveal that the stability and depression difficulty level of pyrites increases in the following order: Fe₃₂S₆₃As < Fe₃₂S₆₄ < Fe₃₂S₆₃AsAu < Fe₃₂S₆₄Au.

Key words:

pyrite; gold; density functional theory; electronic structure; flotability；

1 Introduction

Pyrite (FeS₂) is one of the most widely distributed sulfide minerals in the Earth’s crust, and it often contains precious metals, such as gold. The statistics of 102 types gold deposits show that approximate 85% of the total gold is extracted from the gold-bearing pyrite in these gold deposits [1]. Diverse occurrences of gold have been proposed for the formation of these deposits, including visible and invisible gold. The visible gold mainly occurs as gold inclusions and fracture gold. It has been suggested that visible gold could associate with pyrite through various mechanisms [2–4]. In comparison to visible gold, the existence of invisible gold has been observed as colloidal state, solid solution and nanoparticle (i.e. lattice defects) in pyrite crystal structure [5–9].

Generally, froth flotation is the most widely used method for the preconcentration of gold-bearing pyrite in the industry because of its maturity in technology and advantage in economic cost. Thus, the high-efficiency separation between the gold-bearing pyrite and other minerals plays an important role in gold production at low cost. However, the flotation practices of gold- bearing pyrite often present that flotation quality index fluctuate wildly and flotation process is hard-handle, (i.e. some pyrite is different to be depressed while some pyrite is different to be activated) especially when the invisible gold exists in the pyrite [10–12]. This could be attributed to the fact that the flotation process is extremely complicated and the understanding of properties of pyrite containing invisible gold is deficient [13, 14]. Therefore, an in-depth understanding of the properties of pyrite with invisible gold will aid to improve the flotation mechanism and efficient utilization of gold resource.

The presence of invisible gold is very different to determine by the use of traditional optical or scanning microscopes are it requires more sophisticated modern techniques and rigorous technique of sample preparation. Recently, a number of experimental studies on the invisible gold in pyrite have been performed using various analyses and testing technologies, including electron probe micro analysis (EPMA), laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS), secondary ion mass spectrometry (SIMS) and particle induced X-ray emission (PIXE) [15–20]. These studies provide valuable backgrounds for understanding the occurrence state of Au in pyrite. In spite of this, numerous questions remain unsolved, such as the fact aforementioned method cannot provide information involving the properties of pyrite with invisible gold (in vacuum or in an inert environment), and the scarce experimental data as a result of the rigorous requirements for experimental conditions.

Quantum mechanical computation as an important theoretical simulation method can provide direct observations of atomic- and electro-scale of minerals, and thus it is complementary to modern experimental techniques. However, the application of quantum mechanical computation in the fields of pyrite with invisible gold is seldom. In addition, together with Au, the As also is favored to incorporate into pyrite [21]. Due to the aforementioned reasons, the aim of the present work is to investigate the electronic structures of pyrites with As substitution or interstitial Au or both types by using density functional theory (DFT). Moreover, the effect of the three types of lattice defects on the pyrite flotability was discussed.

2 Computational methods

All of the calculations have been performed using first-principle calculations based on the density functional theory as implemented in Cambridge Sequential Total Energy Package (CASTEP) [22, 23]. Ultrasoft pseudopotentials were employed to represent interactions between the ionic core and the valence electrons. The valence electron configurations considered in this work included Fe 3d⁶4s², S 3s²3p⁴, As4s²4p³, and Au 5d¹⁰6s¹. The generalized gradient approximation (GGA) using the Perdew, Burke, and Ernzerhof (PBE) functionals was employed for the exchange-correlation functional [24]. The convergence of the plane-wave expansion with a kinetic energy cutoff of 330 eV was used throughout the testing. Moreover, a 2×3×1 k-point set was used to define the accuracy of Brillouin zone sampling, which showed that the cutoff energy and k-point mesh were sufficient for the system. For self-consistent electronic minimization, the pulay density mixing method was employed at a convergence tolerance of 2.0×10^-6 eV/atom. The convergence criteria for structure optimization and energy calculation were set to 1) an energy tolerance of 1.22×10^-6 eV/atom, 2) a maximum force tolerance of 0.05 eV/ and 3) a maximum displacement tolerance of 0.002 .

The geometry optimization of pyrite (FeS₂) unit cell belongs to the space group Pa3 with Fe cations on the corners and the face-centered positions in a cubic cell. By analogy to the NaCl structure, Fe atoms occupy the sodium positions and the center of each S—S bond in the disulfide group is located at the chloride positions. Each Fe atom is coordinated to 6 S atoms in an octahedron that is slightly distorted, in which it is compressed along one of the trigonal axes. Each S atom is coordinated to 3 Fe atoms and 1 S atom in a tetrahedral configuration, as shown in Fig. 1(a). The 2×2×2 geometry optimized supercell pyrite (Fe₃₂S₆₄) is shown in Fig. 1(b). In order to simulate the actual nature pyrite, a 2×2×2 supercell is constructed to model the bulk pyrite with one As atom substituting one S atom (Fe₃₂S₆₃As); with one Au atom in an interstitial lattice site (Fe₃₂S₆₄Au); and with both type lattice defects (Fe₃₂S₆₃AsAu), as shown in Fig. 2.

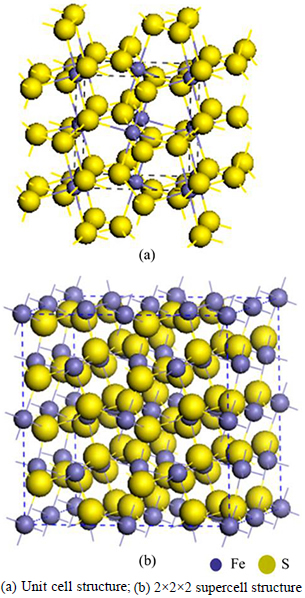
Fig. 1 Theoretical model of pyrite bulk:(In region of blue dotted line)

The incorporation energy refers to the required energy when an Au atom incorporates into the crystal. Here, the incorporation energy of an Au atom in the pyrite lattice, i.e. △E_Au is defined as follows [25]:

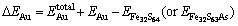        (1)

where 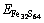and 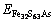are the total energies of pyrite with incorporated Au, perfect pyrites and pyrite with As substitution, respectively. E_Au is defined as the calculated total energies of the incorporated Au matrix atom, i.e. pseudo atomic energy, which is calculated during the optimized process of the cell. The lower the value of △E_Au is the more favorable the Au is to incorporate into pyrite. Analogously, the substitution energy of As in Fe₃₂S₆₃As is obtained as –706.98 kJ/mol. It suggests that As is energetic to substitute the S atom in pyrite.

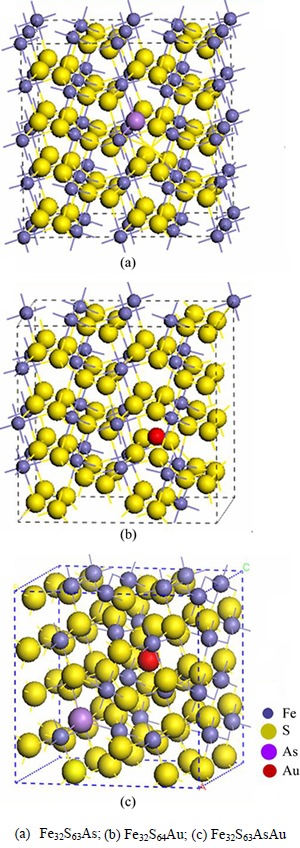
Fig. 2 Models of 2×2×2 pyrite supercells:

3 Results and discussion

3.1 Incorporation energy of Au into pyrite

The incorporation energy of Au atom is calculated to evaluate the incorporation tendency of Au into pyrite (Fe₃₂S₆₄ and Fe₃₂S₆₃As), as shown in Table 1. The high negative value of incorporation energy of Au in Fe₃₂S₆₄Au and Fe₃₂S₆₃AsAu suggests that the Au is very energetic to incorporate in pyrite as these forms, as seen in Fig. 2. The incorporation of Au is more favorable to occur on interstitial lattice site of pyrite in the absence of As substitution, due to the fact that it possesses lower incorporation energy in Fe₃₂S₆₄Au than in Fe₃₂S₆₃AsAu. In addition, as a result of Au incorporation, the pyrite supercell should expand outward. However, it is shown that the incorporation of Au atom results in a negligible expansion of the pyrite lattice parameters (i.e. 10.846 of Fe₃₂S₆₄Au and 10.844 of Fe₃₂S₆₃AsAu). This result presents that the geometric construction of pyrite with Au incorporation established is that this investigation is extremely stable, and it insures the accuracy of electronic structure analysis below. The covalent radius of Au (1.34 ) is much greater than that of S (1.02 ), Fe (1.17 ) or As (1.20 ). The results imply that the pyrite structure would be relative stable when Au is incorporated into pyrite.

Table 1 Incorporation energy of Au in pyrite crystal and influence of its incorporation on lattice parameters of crystal

Table 2 shows the distance between interacting atoms in various pyrites. From Table 2, it can be seen that when Au is incorporated on interstitial lattice site of pyrite (Fe₃₂S₆₄Au), the bond lengths of Au—S (2.416 ) and Au—Fe (2.653 ) are greater than those of the S—S (2.220 ) and S—Fe (2.226 ) bonds in perfect pyrite (Fe₃₂S₆₄), respectively, which resulted in the expansion of the pyrite crystal. For the case of Fe₃₂S₆₃AsAu, the bond lengths of Au—S (2.637 ) and Au—Fe (2.943 ) are much longer than the Fe—S, S—S, As—Fe bonds in Fe₃₂S₆₄AuAs, which results in more expansion of the pyrite crystal. Moreover, in Table 2, the calculated Mulliken population between interacting atoms in pyrite is also investigated. It can be seen that Au atoms obviously change the bond population in pyrites. The population of the Fe—S and Fe—As bonds significantly increases and the covalence strengthens, while the population of the S—S bond decreases and the covalence weakens. It likely alters the attraction between the water dipole and the pyrite surface, and thereby influences the natural flotability of pyrites. In addition, it is found that ionicity Au—S bonds (population close to 0) and antibonding states of Au—Fe bonds are formed in the pyrite with incorporated Au, and these bonds formation compensates for the energy consumption of the structural expansion, which contributes to the stability of the crystal structure. The population of Au—S bond in Fe₃₂S₆₃Au is greater than that in Fe₃₂S₆₃AsAu, and the covalence level of the former is greater than that of the latter, and the latter presents a stronger ionic character. The covalent Au—S interaction can be clearly seen in the charge density in Fig. 3.

Table 2 Mulliken overlap population and distance between interacting atoms in pyrite

Fig. 3 Electron density maps of Fe₃₂S₆₄Au (a) and Fe₃₂S₆₃AsAu (b) (Bracketed numbers indicate atomic charge)

3.2 Electronic structure details of pyrite with incorporated Au

Figure 4 shows the band structures of four type pyrites (the zero of the energy is set at the Fermi level, E_f). From Fig. 4(a), it can be seen that the conduction band minimum (CBM) and the valence band maximum (VBM) are located at the G and Q points, respectively in perfect pyrite, which suggests that the perfect pyrite acts as an indirect gap semiconductor. In comparison to perfect pyrite, the presence of only As substitution causes a similar band-gap, except the As impurity level located at bottom of valence band (Fig. 4(b)). This result indicates that the property of pyrite only with As substitution (Fe₃₂S₆₃As) is similar to perfect pyrite. However, the band structures of pyrite would be significantly affected by the incorporated Au. In Figs. 4(c) and (d), the Au impurity energy levels are introduced into the energy band near the conduction band zone, which suggests that the incorporation of Au changes a p-type pyrite to an n-type pyrite. This result is consistent with the investigation reported by TOMM et al [26]. In addition, the band-gaps of Fe₃₂S₆₄Au (0.184 eV) and Fe₃₂S₆₃AsAu (0.335 eV) are much lower than those of the Fe₃₂S₆₄ (0.55 eV) and Fe₃₂S₆₃As (0.54 eV), and it is attributed to the fact that electrons from Au atom fill unoccupied orbital of S atom. These results indicate that the incorporation of Au observably increases the semi- conductivity of pyrite. In conclusion, the semi- conductivity of pyrites increases in the following order: Fe₃₂S₆₄<>₃₂S₆₃As<>₃₂S₆₃AsAu<>₃₂S₆₄Au.

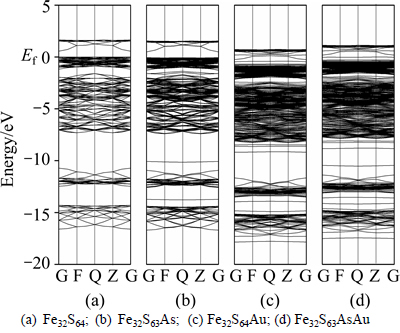
Fig. 4 Band structures of pyrites:

Xanthate is widely used collector in the flotation system for pyrites, and the adsorption of the collector on the pyrite surface primarily occurs via oxidation of xanthate ions (X^–) to dixanthogen (X²):

2X^–2X²+2e

This process depends on the electron transfer from xanthate ions to pyrite, while the electron transfer depends on the level of conduction band and the valence band [27, 28]. Pyrite possessing of a lower band-gap is more active to transfer electron from xanthate to the oxidant (O₂ or Fe³⁺) [29], i.e., more actively oxidizing xanthate to dixanthogen and then enhancing the electrochemical adsorption of dixanthogen on the pyrite surface. Thus, the pyrites with incorporated Au are more likely to accelerate the formation and adsorb dixanthogen. On the other hand, the adsorption stability of dixanthogen on pyrite surface is signally influenced by the edge level of pyrite, which is reflected as the appearance of dixanthogen desorption with the increase of pyrite conduction band edge level [28]. From Fig. 4, the incorporation of Au results in the significant decrease conduction band edge level of pyrite, and the Fe₃₂S₆₄Au possesses the lowest conduction band edge level. It implies that the dixanthogen on the pyrite surface is more difficult to be desorbed when the pyrite has Au incorporation.

The partial DOS and total DOS of four type pyrites are presented in Fig. 5, the zero of the energy is set at the Fermi level, E_f. The DOS contribution of perfect pyrite is mainly originated from Fe 3d, S 3s and S 3p orbital (Fig. 5(a)). In Fig. 5(b), the impurity level locating at –10.5 and –13.7 eV corresponds to the As 4s orbital, and locating in the range of –7.5 to 0 corresponds to the As 4p orbital. In comparison to perfect pyrite, an inconspicuous positive shift of the total DOS for pyrite only with As substitution (Fe₃₂S₆₃As) is observed. From Figs. 5(c) and (d), it can be seen that the DOS of the Au atom is mainly derived from the 5d orbital. The dispersion of the valence band located on the S 3p and Au 5d area increases and widens, which corresponds to the enhancement of hybridization between the Au 5d and S 3p (As 4p), and thus enhancement of pyrite stability. Moreover, the gap between the split Fe 3d t_2g and 3d e* g is lowered. These results indicate that the correlation effects between the Fe 3d electrons are enhanced due to the incorporation of Au. Hence, it is demonstrated again that the pyrite structure would become more stable due to the incorporation of Au atom. This result well agrees with the lattice parameter analysis in section 3.1. However, the effect of incorporated Au on the stability level of different pyrite species (Fe₃₂S₆₄Au and Fe₃₂S₆₃AsAu) is very different. Compared to the DOS of perfect pyrite, the DOS of Fe₃₂S₆₄Au and Fe₃₂S₆₃AsAu becomes more negative by approximately 1.5 eV and 1 eV, respectively, and there are almost no DOS crossing the Fermi level. This result suggests that the stability and oxidizability of pyrite with incorporated Au significantly increases, and the stability and oxidizability of Fe₃₂S₆₄Au is greater than Fe₃₂S₆₃AsAu. It could be concluded that the stability and oxidizability of pyrites increases in the following order: Fe₃₂S₆₃As<>₃₂S₆₄<>₃₂S₆₃AsAu< Fe₃₂S₆₄Au. The energy magnitude of pyrites also supports this conclusion.

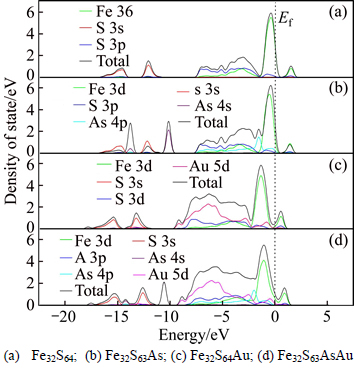
Fig. 5 Partial and total DOS of pyrites:

The depression of pyrite in industry is often achieved via the strong oxidization of pyrite surface, in which the Fe(III)-hydroxy and Fe(III)-oxide hydrophilic species are formed on pyrite surface [11, 28]. In the present work, it is found that the incorporated Au results in a decrease of the split Fe 3d t_2g and 3d e* g, and an decrease of the energy level of total pyrite DOS. This result suggests that the depression of incorporated Au pyrite is much more difficult than pyrite without incorporated Au. In conclusion, the greater the stability and oxidizability of pyrite is, the more difficult the pyrite is to be oxidized and depressed in the flotation process. These results would provide a better understanding of flotation differences between pyrites with gold-bearing type.

4 Conclusions

1) In the present work, the density functional theory calculation is employed to investigate formation and electronic structure of pyrite with incorporated Au, and the effect of incorporated Au on the pyrite flotability is discussed. By calculating the incorporation energy of Au in Fe₃₂S₆₄Au and Fe₃₂S₆₃AsAu crystal, it is found that Au would favor to exist in these pyrite crystals, and it results in a small expansion of pyrite cell. The ionicity Au—S bonds and antibonding states of Au—Fe bonds are formed in the pyrite as the incorporation of Au. However, from the magnitudes of incorporation energy of Au, it suggests that the incorporation of Au more energetic occurs in Fe₃₂S₆₄Au than that in Fe₃₂S₆₃AsAu. In addition, the incorporation of Au affects the covalence level of the S—Fe and S—S bonds, which alters the natural flotability of pyrites.

2) The incorporation of Au significantly decreases the band-gap and increases the semi-conductivity of pyrite. The semi-conductivity of pyrites increases in the following order: Fe₃₂S₆₄<>₃₂S₆₃As<>₃₂S₆₃AsAu< Fe₃₂S₆₄Au. The higher semi-conductivity is advantageous for the formation and adsorption of dixanthogen in pyrite flotation.

3) The incorporation of Au significantly increases the oxidizability of pyrite. The stability and oxidizability of pyrites increases in the following order: Fe₃₂S₆₃As< Fe₃₂S₆₄<>₃₂S₆₃AsAu<>₃₂S₆₄Au. The greater the stability and oxidizability of pyrite is, the more difficult the pyrite is to be oxidized and depressed in the flotation process.

References

[1] GAO Zhen-min, YANG Zhu-sen, LI Hong-yang, LUO Tai-yi, YAO Lin-bao, RAO Wen-bo. Genesis and characteristics of gold hosted by pyrite [J]. Geol J China Univ, 2000, 6(2): 156–162.

[2] SU Wen-chao, XIA Bin, ZHANG Hong-tao, ZHANG Xing-chun, HU Rui-zhong. Visible gold in arsenian pyrite at the Shuiyindong Carlin-type gold deposit, Guizhou, China: Implications for the environment and processes of ore formation [J]. Ore Geology Reviews, 2008, 33(3): 667–679.

[3] HAZARIKA P, MISHRA B, CHINNASAMY S S, BERNHARDT H J. Multi-stage growth and invisible gold distribution in pyrite from the Kundarkocha sediment-hosted gold deposit, eastern India [J]. Ore Geology Reviews, 2013, 55(4): 134–145.

[4] JHA V, SINGH S, VENKATESH A S. Invisible gold occurrence within the quartz reef pyrite of Babaikundi area, North Singhbhum fold-and-thrust belt, Eastern Indian Shield: Evidence from petrographic, SEM and EPMA studies [J]. Ore Geology Reviews, 2015, 65: 426–432.

[5] MILLS S E, TOMKINS A G, WEINBERG R F, FAN Hong-rui. Implications of pyrite geochemistry for gold mineralisation and remobilisation in the Jiaodong gold district, northeast China [J]. Ore Geology Reviews, 2015, 71: 150–168.

[6] DEDITIUS A P, UTSUNOMIYA S, REICH M, KESLER S E, EWING R C, HOUGH R, WELSHE J. Trace metal nanoparticles in pyrite [J]. Ore Geology Reviews, 2011, 42(1): 32–46.

[7] HOUGH R, REICH M. Noble metal nanoparticles in ore systems [J]. Ore Geology Reviews, 2011, 42: 55–60.

[8] PALENIK C S, UTSUNOMIYA S, REICH M, KESLER S E, WANG L M, EWING R C. “Invisible” gold revealed: Direct imaging of gold nanoparticles in a Carlin-type deposit [J]. Am Mineral, 2004, 89(10): 1359–1366.

[9] WEI Jun-hao, TAN Wen-juan, GUO Da-zhao, TAN Jun, LI Yan-hua, YAN Yun-fei. Isotope systematics and metallogenetic age of Zhuanghe gold deposit, Liaoning province [J]. Journal of Central South University of Technology, 2007, 14(1): 104–110.

[10] SUN Zhong-mei, SUN Chun-bao, WANG Ji-zhen, YIN Wan-zhong. Optimization and mechanism of gold-bearing sulfide flotation [J]. Rare Metals, 2014, 33(3): 363–368.

[11] PAK T H, SUN Ti-chang, XU Cheng-yan, JO Y H. Flotation and surface modification characteristics of galena, sphalerite and pyrite in collecting-depressing-reactivating system [J]. Journal of Central South University of Technology, 2012, 19(6): 1702–1710.

[12] GU Guo-hua, SUN Xiao-jun, LI Jian-hua, HU Yue-hua. Influences of collector DLZ on chalcopyrite and pyrite flotation [J]. Journal of Central South University of Technology, 2010, 17(2): 285–288.

[13] ZHONG Shui-ping, WU Zhi, HUANG Zhong-sheng, RUAN Ren- man. Oxidation kinetics reaction of gold-bearing pyrite in sulphuric acid [J]. Chin J Rare Met, 2013, 37(2): 295–301.

[14] LIU You-cai, ZHU Zhong-si, FU Jian-gang, LI Li-feng, LIN Qing- quan, LI Zhi-hui. Leaching gold ores by lime-sulphur-synthetic- solution with alkali-catalyzed process [J]. Chin J Rare Met, 2013, 37(1): 123–129. (in Chinese)

[15] REICH M, KESLER S E, UTSUNOMIYA S, PALENIK C S, CHRYSSOULIS S L, EWING R C. Solubility of gold in arsenian pyrite [J]. Geochim Cosmochim Ac, 2005, 69(11): 2781–2796.

[16] AGANGI A, HOFMANN A, WOHLGEMUTH-UEBERWASSER C C. Pyrite zoning as a record of mineralization in the Ventersdorp Contact Reef, Witwatersrand Basin, South Africa [J]. Econ Geol, 2013, 108(6): 1243–1272.

[17] LARGE R R, MASLENNIKON V V, ROBERT F, DANYUSHEVSKY L V, CHANG Z. Multistage sedimentary and metamorphic origin of pyrite and gold in the giant Sukhoi Log deposit, Lena gold province, Russia [J]. Econ Geol, 2007, 102(7): 1233–1267.

[18] LARGE R R, DANYUSHEVSKY L, HOLLIT C, MASLENNIKOV V, MEFFRE S, GILBERT S, BULL S, SCOTT R, EMSBO P, THOMAS H. Gold and trace element zonation in pyrite using a laser imaging technique: Implications for the timing of gold in orogenic and Carlin-style sediment-hosted deposits [J]. Econ Geol, 2009, 104(5): 635–668.

[19] DEDITIUS A P, REICH M, KESLER S E, UTSUNOMIYA S, CHRYSSOULIS S L, WALSHE J, EWING R C. The coupled geochemistry of Au and As in pyrite from hydrothermal ore deposits [J]. Geochim Cosmochim Ac, 2014, 140: 644–670.

[20] DEDITIUS A P, UTSUNOMIYA S, RENOCK D, EWING R C, RAMANA C V, BECKER U, KESER S E. A proposed new type of arsenian pyrite: Composition, nanostructure and geological significance [J]. Geochim Cosmochim Ac, 2008, 72(12): 2919– 2933.

[21] BLANCHARD M, ALFREDSSON M, BRODHOLT J, WRIGHT K, CATLOW C. Arsenic incorporation into FeS₂ pyrite and its influence on dissolution: A DFT study [J]. Geochim Cosmochim Ac, 2007, 71(3): 624–630.

[22] SEGALL M D, LINDAN P, PROBERT M J, PICKARD C, HASNIP P, CLARK S, PAYNE M C. First-principles simulation: Ideas, illustrations and the CASTEP code [J]. J Phys: Condens Matt, 2002, 14(11): 2717–2744.

[23] KRESSE G, JOUBERT D. From ultrasoft pseudopotentials to the projector augmented-wave method [J]. Phys Rev B, 1999, 59(3): 1758–1775.

[24] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Phys Rev Lett, 1996, 77(18): 3865– 3868.

[25] NISHIDATE K, YOSHIZAWA M, HASEGAWA M. Energetics of Mg and B adsorption on polar zinc oxide surfaces from first principles [J]. Phys Rev B, 2008, 77(3): 035330.

[26] TOMM Y, SCHIECK R, ELLMER K, FIECHTER S. Growth mechanism and electronic properties of doped pyrite (FeS₂) crystals [J]. J Crys Growth, 1995, 146(1): 271–276.

[27] CHANDRA A P, GERSON A R. A review of the fundamental studies of the copper activation mechanisms for selective flotation of the sulfide minerals, sphalerite and pyrite [J]. Advances in Colloid & Interface Science, 2009, 145(1, 2): 97–110.

[28] CHEN Jian-hua, FENG Qi-ming, LU Yi-ping. Energy band model of electrochemical flotation and its application: II. Energy band model of xanthate interacting with sulphide minerals [J]. Chin J Nonferrous Met, 2000, 10: 426–429. (in Chinese)

[29] LI Quan, QIN Wen-qing, SUN Wei, QIU Guan-zhou. Calculation of electron structure by density function theory and electrochemical process of surface (100) of FeS₂ [J]. Journal of Central South University of Technology, 2007, 14(5): 618–622.

(Edited by FANG Jing-hua)

Cite this article as:

LIU Dan, WANG Yi-jie, XIAN Yong-jun, WEN Shu-ming. Electronic structure and flotability of gold-bearing pyrite: A density functional theory study [J]. Journal of Central South University, 2017, 24(10): 2288–2293.

Foundation item: Projects(51504109, 51504107) supported by the National Natural Science Foundation of China

Received date: 2016-06-25; Accepted date: 2016-10-07

Corresponding author: XIAN Yong-jun, Lecturer, PhD; E-mail: 61470281@qq.com

Abstract: Various incorporation of Au in pyrite and its effects on the geometrical structure, electronic structure and flotability of pyrite were theoretically investigated and fully discussed by performing density functional theory (DFT). The calculated incorporation energy shows that gold would most likely exist in pyrite via incorporating into interstitial lattice sites in the absence of As impurity. As a result of incorporated Au, the covalence levels of the S—Fe and S—S bonds are changed, and the tonicity of Au—S bonds and antibonding of Au—Fe bonds are found to form in the pyrite, which would change the natural flotability of pyrite. The Au impurity energy levels are introduced into the energy band and result in the transformation of pyrite semiconductivity type. The calculated band-gap value suggests that the incorporated Au significantly decreases pyrite semiconductivity level, which enhances the formation and the adsorption stability of dixanthogen during pyrite flotation. The DOS results reveal that the stability and depression difficulty level of pyrites increases in the following order: Fe₃₂S₆₃As < Fe₃₂S₆₄ < Fe₃₂S₆₃AsAu < Fe₃₂S₆₄Au.