J. Cent. South Univ. (2012) 19: 1311-1316
DOI: 10.1007/s11771-012-1143-x
Generic reconstruction technology based on RST for multivariate time series of complex process industries
KONG Ling-shuang(孔玲爽)1, YANG Chun-hua(阳春华)2, LI Jian-qi(李建奇)2,
ZHU hong-qiu(朱红求)2, WANG Ya-lin(王雅琳)2
1. College of Electrical and Information Engineering, Hunan University of Technology, Zhuzhou 412000, China;
2. School of Information Science and Engineering, Central South University, Changsha 410083, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract:
In order to effectively analyse the multivariate time series data of complex process, a generic reconstruction technology based on reduction theory of rough sets was proposed. Firstly, the phase space of multivariate time series was originally reconstructed by a classical reconstruction technology. Then, the original decision-table of rough set theory was set up according to the embedding dimensions and time-delays of the original reconstruction phase space, and the rough set reduction was used to delete the redundant dimensions and irrelevant variables and to reconstruct the generic phase space. Finally, the input vectors for the prediction of multivariate time series were extracted according to generic reconstruction results to identify the parameters of prediction model. Verification results show that the developed reconstruction method leads to better generalization ability for the prediction model and it is feasible and worthwhile for application.
Key words:
complex process industry; prediction model; multivariate time series; rough sets；
1 Introduction
Time series data are pervasive in complex process industries such as metallurgy, power, steel, and petrochemical engineering. Therefore, analysis of time series data from these complex systems is very important for modelling, predicting, control and other purposes [1]. It is a routine in the analysis of time series data from a nonlinear system to make a phase space reconstruction based on Taken’s embedding theorem [2]. The basic idea of the analysis is that the original series is decomposed into multi- subseries with the same dimension to review the dynamics of the underlying system. From the modelling point of view, to reconstruct the phase space of time series data is equivalent to extract the effective input vector of the prediction model to generate more accurate forecasts [3-4]. In the published literatures, there have been many discussions on how to reconstruct the phase space of time series based on Taken’s theorem and its extensions. The basic methods which are usually used to choose the embedding dimension and the time-delay parameter include false nearest neighbors (FNN) [5], singular value decomposition (SVD) [6], mutual information and autocorrelation [7] etc. As CAO et al [8] pointed out, these methods are more or less subjective in determining the embedding parameters. In order to calculate the optimal embedding parameters, there are other methods and some modified methods developed based on the above methods, such as minimum mean one-step prediction error method [9], FMMI/FNN method [10], and fill factor method [11].
Unfortunately, so far, there does not exist one uniform construction method especially for multivariate time series. In fact, multivariate time series data contain more information than univariate time series data and are available in many process industries. However, due to the complexity of process itself and the subjectivity of human operation, multivariate time series from complex process industries is usually noisy, fuzzy and incomplete, even contains redundant and wrong information, which are called the uncertainty in this work. The uncertainty of data makes it difficult to reconstruct the phase space of multivariate time series from complex process industries by utilizing the existing methods.
Rough set theory (RST), which was introduced by PAWLAK in the early 1980s, is an effective mathematical tool to handle uncertainty and vagueness.
It focuses on the discovery of pattern in inconsistent data and can be used as the basis to perform formal reasoning under uncertainty, machine learning, and rule discovery. In the past decades, the rough set theory has been successfully applied to many real-world problems in medicine, pharmacology, engineering and financial analysis [12]. In this work, the rough set theory was applied to the reconstruction procedure of multivariate time series data from complex process industries. By combining the reduction technology of rough set theory with the classical reconstruction technology, a generic reconstruction technology was proposed to extract the simplified input vector of prediction model from multivariate time data. The developed method is applied to reconstructing and predicting the time series of returned material in blending process of alumina production.
2 Original reconstruction of multivariate time series
Suppose that there are M variables measured at the same time in a process industry, and the time series of the i-th variable xi is {xi,j}, i=1, 2,…, M, j=1, 2,…, N. Firstly, the multivariate time series consisting of M univariate time series is transformed into an univariate time series Y, i.e.,
(1)
Then, based on Taken’s embedding theorem, a time-delay vector can be reconstructed as follows:
…,
n=N1, N1+1, …, N, 
(2)
where τi and di, i=1, 2, …, M, are the time-delays and the embedding dimensions, respectively. Following the embedding theorem, if each di is sufficiently large, there exists the function Fi(·) such that
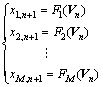(3)
The key problem is how to choose the time-delay τi and embedding dimensions di, i=1, 2, …, M, so that Eq. (3) holds. Considering that recent delays are more important than the old delays in practical industries, set τi=1 for each of univariate time series x1,j, x2,j,…, xM,j. And the embedding dimensions are found by minimizing the mean one-step prediction error [8] that is one of the existing methods. However, it is very difficult to obtain the optimal di due to the uncertainty of time series data from complex process industries. That is to say, the embedding dimensions obtained by the above method can be larger or less than the optimal ones. The larger embedding dimension increases the computing time and space, and the less one cannot contain the full information of original time series data. To overcome the problem, the embedding margins Δdi are considered:
(4)
where
is the embedding dimension of the i-th univariate time series obtained by minimizing the mean one-step prediction error, and Δdi is the compensated margin which is determined according to the production experience. Then, the decision-table of time series data is constructed by utilizing the reconstruction vector in Eq. (2) and the redundant and uncertain information is handled by the reduction theory of rough set to obtain the optimal reconstruction of multivariate time series data with uncertainty.
3 RST-based generic reconstruction of multivariate time series
The core of RST is the attribute reduction based on the decision-table. So, the original attribute decision-table of time series data has to be built for the reduction of the reconstruction vector in Eq. (2).
3.1 Decision-table construction of multivariate time series
Suppose that the i-th variable is the predicted variable (key variable), the decision-table in Table 1 is constructed by taking xi,n+1 as the decision attribute and Vn as the condition attribute. Thus, the number of the condition attribute is z according to Eq. (2). RST can only handle the discrete attribute, so the natural discrete method [13], which divides the interval of continuous data into many uniform subintervals, is adopted to realize the discrimination of the continuous time series data from the production field. If the i-th variable is discrete as k subintervals and ci,k denotes the k-th subinterval of the i-th variable, the continuous decision-table is converted into the original decision-table S in Table 1. Here, 
, where U is the universe, C is the condition attribute, D is the decision attribute, V is the set of attribute values, and f is a information function which defines a attribute value for each object of U.
Table 1 Original decision-table of multivariate time series
3.2 RST reduction and generic reconstruction
The common method of the reducing attributes of decision-table is to generate discernibly function, then reducing discernibly function and achieving the attributes reduction of the decision-table. But, the reduction method has high time and space complexity, which leads to its incompetence in many practical situations. The genetic algorithm (GA) is a global search algorithm based on the mechanisms of natural selection and “survival of the fittest” from natural evolution, and it has the advantages of simplicity, robustness and high efficiency [14-15]. On the other hand, it is convenient to represent the reducing attribute problem by 0/1 binary encoded strings. Therefore, GA is used to solve the reduction problem of the attributes of decision-table.
1) Optimization variable and chromosome encoding
Set pk as the k-th condition attribute in the decision-table, and the optimization variable is P in Eq. (5):
(5)
P is also the chromosome encoded by 0/1 binary, where 1 represents “selected” and 0 represents “not”.
2) Two-stage optimization model
In order to find the reduction with minimum condition attributes, the optimization model is constructed as follows:
(6)
(7)
Equation (6) is the optimization objective in which F(P) is the objective function, i.e., the number of condition attribute of chromosome; Eq. (7) is the constraints in which γ(P, D) is the constraint function, i.e., the dependence degree of the decision attribute D to the condition attribute set P, and card á·? is the number of elements in the attribute set.
3) Fitness function
Based on the penalty strategy of the optimization problem with constraints, the fitness function f(P) is built by introducing the constraints into the optimization objective:
f(P)=1-F(P)+γ(P, D)
By this fitness function, the two-stage optimization problem is turned into the single objective problem without constraints.
4) Evolution strategy
In the evolution progress, the elite selection strategy is adopted and the probabilities of crossover and mutation are calculated by the improved algorithm presented in Ref. [14]. If the fitness function value of the optimal individual is unchanged in continuous generations or the evolving process reaches the maximum generation predetermined, the evolution terminates and returns the best solution in current population as the reduced condition attribute set C′. Thus, Eq. (2) is reformulated as
,
…,
S≤M, 0≤ai1< ai2< ai3<,…≤di-1 (8)
where 
is the time-delay of the i-th variable and 
is the value of the i-th variable at time 
. Thus, Eq.(3) is rewritten as follows:
(9)
Compared with the original reconstruction space in Eq. (2), the dimension of the vector space obtained by the reduction of RST is reduced and the time series is no longer embedded with the equal time interval. To distinguish the method of reconstruction, the phase space denoted by Eq. (8) is called the generic reconstruction phase space. By the generic reconstruction, not only the redundant embedding attributes are deleted, but also the variables irrelevant with the key variable can be removed from the original reconstruction space, which avoids the relation analysis of multivariate time series. According to the generic reconstruction result, the sample set for modeling and forecasting multivariate time series can be extracted by taking the reduced condition attribute sets C′ as the input vector Xn and the decision attribute as the output yn.
Let
, 
(10)
The sample set is denoted by (Xn, yn), n=1, 2, …, L, and L is the number of samples.
4 Verification of industrial case
In order to demonstrate the efficiency and superiority of the proposed reconstruction technology, the time series data from the blending process of alumina production are used to build the prediction model for the composition of returned material, in which the prediction model 
is learned by the Least Squares Support Vector Machines (LS_SVM) [16] and its training sample sets are extracted by the proposed reconstruction technology.
The returned material is composed of six oxides which are CaO (x1), Na2O (x2), SiO2 (x3), Fe2O3 (x4), Al2O3 (x5), and H2O (x6). The concentrations of five oxides are offline measured in the laboratory and the interval of sampling is 1 h, so the measured results constitute a multivariate time series with uniform time interval. Two hundred and forty sample data were continuously colleted in ten days, the first 120 samples were used to extract the input vector and to train the LS_SVM and the rest were used to test.
Without loss of generality, the content of CaO is selected to be the predicted variable. The embedding dimension calculated by minimizing the mean one-step prediction error is five, i.e., 
(i=1, 2,…, 6). If set ?di=3, so di=8 according to Eq. (4), that is, the dimension of the original reconstruction space is 48. After reducing the original reconstruction space by RST, the dimension of the phase space is 14, i.e.,
According to the original reconstruction result and the generic reconstruction result, 100 input-output samples were extracted to train the LS_SVM, in which the kernel function is radial basis function (RBF), kernel function parameter is 10 and error warning factor is 200. The simulation results of LS_SVM based on the original reconstruction space (ORS) and those based on the generic reconstruction space (GRS) are shown in Fig. 1 and Fig. 2, respectively. It can be obviously seen that the LS_SVM based on GRS has less prediction error and the better fitting degree of prediction result and real result, which means that the proposed reconstruction technology has the better recognition ability of model.
To further demonstrate the validity of the generic reconstruction technology, the contents of other oxides were also predicted and the results are shown in Table 2 where the maximum relative estimated error (Emax) in Eq. (11) and the relative root mean square error (ERMS) in Eq. (12) are used as the criteria:
(11)
(12)
where yi and 
are the measurement values obtained from the laboratory and the corresponding model output, respectively.
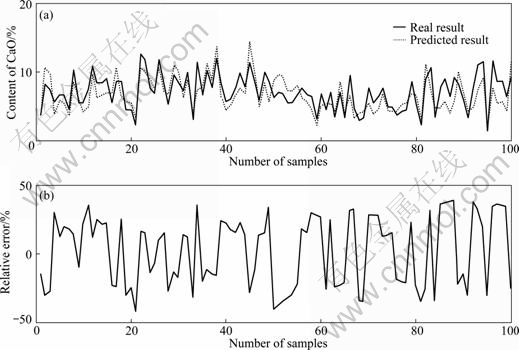
Fig.1 Simulation results of LS_SVM based on ORS
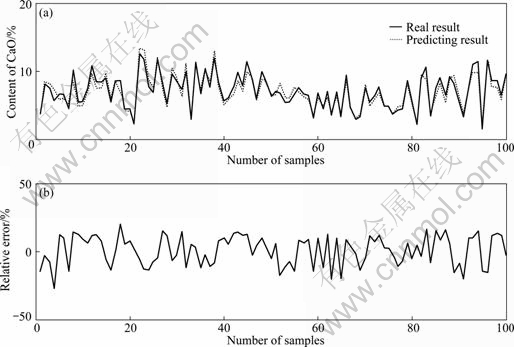
Fig.2 Simulation results of LS_SVM based on GRS
From Table 2, it can be seen that the relative root mean square error of LS_SVM model based on GRS is less than 13%, which means that the prediction can well track the trend of time series data. The less maximum prediction error indicates that the model has better precision.
Table 2 Performance comparison of two methods
5 Conclusions
1) Based on the uncertainty of multivariate time series data from complex process industries, a generic phase space reconstruction technology is proposed by combining the classical reconstruction method with the reduction technology of rough set theory.
2) The proposed generic reconstruction technology can be used to extract the input vector for the prediction of time series and to identify the predictive and non-predictive functional relationships between different time series, so it is an effective way to analyze the multivariate time series data.
3) Utilizing the proposed reconstruction technology, the LS_SVM is built to predict the dynamics using multivariate time series for a blending process. The simulation results show that the model has high prediction accuracy and good generalization ability, and can well track the trend of time series, which has high potential for optimization and control of process industries.
References
[1] HU Zhi-kun, XU Fei, GUI Wei-hua, YANG Chun-hua. Wavelet matrix transform for time-series similarity measurement [J]. Journal of Central South University of Technology, 2009, 16(5): 802-806.
[2] XI Jian-hui, HAN Min. Prediction of multivariate time series based on principal component analysis and neural networks [J]. Control Theory & Applications, 2007, 24(5): 719-724. (in Chinese)
[3] LEUNG H, LO T, WANG S. Prediction of noisy chaotic time series using an optimal radial basis function neural network [J]. IEEE Transactions on Neural Networks, 2001, 12(5): 1163-1172.
[4] HAN Min, XI Jian-hui, XU Shi-guo, Yin Fu-liang. Prediction of chaotic time series based on the recurrent predictor neural network [J]. IEEE Transactions on Signal Processing, 2004, 52(12): 3409-3416.
[5] KENNEL M B, BROWN R, ABARBANEL H D I. Determining embedding dimension for phase-space reconstruction using a geometrical construction [J]. Physical Review A, 1992, 45(6): 3404-3411.
[6] KEMBER G, FOWLER A C. A correlation function for choosing time delays in phase portrait reconstruction [J]. Physics Letters A, 1993, 179(2): 72-80.
[7] FRASER A M, SWINNEY H L. Independent coordinates for strange attractors form mutual information [J]. Physical Review A, 1986, 33(2): 1134-1140.
[8] CAO L, MEES A, JUDD K. Dynamics from multivariate time series [J]. Physica D, 1998, 121(1-2): 75-88.
[9] KIM H S, EYKHOLT R, SALAS J D. Nonlinear dynamics, delay times, and embedding windows [J]. Physica D, 1999, 127(2): 48-60.
[10] KENNEL M B. False neighbors and false strands: A reliable minimum embedding dimension algorithm [J]. Physical Review E, 2002, 66(2): 1-18.
[11] BUZUG T, PFISTER G. Optimal delay time and embedding dimension for delay-time coordinates by analysis of the global static and local dynamical behavior of strange attractors [J]. Physical Review A, 1992, 45(10): 7073-7084.
[12] SHEN Li-xiang, FRANCIS E H T, QU Liang-sheng, SHEN Yu-di. Fault diagnosis using rough sets theory [J]. Computers in Industry, 2000, 43(1): 61-72.
[13] JELONEK J, KRAWIEC K, SLOWINSKI R. Rough set reduction of attributes and their domains for neural networks [J]. Computational Intelligence, 1995, 11(2): 339-347.
[14] YANG Chun-hua, GUI Wei-hua, KONG Ling-shuang, WANG Xiao-li. A genetic-algorithm-based optimal scheduling system for full-filled tanks in the processing of starting materials for alumina production [J]. Canadian Journal of Chemical Engineering, 2008, 86(4): 804-812
[15] YU Shou-yi, KUANG Su-qiong. Fuzzy adaptive genetic algorithm based on auto-regulating fuzzy rules [J]. Journal of Central South University of Technology, 2010, 17(1): 123-128.
[16] SONG Hai-ying, GUI Wei-hua, YANG Chun-hua, PENG Xiao-qi. Application of dynamical prediction model based on kernel partial least squares for copper converting [J]. The Chinese Journal of Nonferrous Metals, 2007, 17(7): 1201-1206. (in Chinese)
(Edited by YANG Bing)
Foundation item: Project(61025015) supported by the National Natural Science Funds for Distinguished Young Scholars of China; Project(21106036) supported by the National Natural Science Foundation of China; Project(200805331103) supported by Research Fund for the Doctoral Program of Higher Education of China; Project(NCET-08-0576) supported by Program for New Century Excellent Talents in Universities of China; Project(11B038) supported by Scientific Research Fund for the Excellent Youth Scholars of Hunan Provincial Education Department, China
Received date: 2011-03-18; Accepted date: 2011-06-15
Corresponding author: KONG Ling-shuang, PhD; Tel: +86-18273371476; E-mail: konglingsh@126.com
Abstract: In order to effectively analyse the multivariate time series data of complex process, a generic reconstruction technology based on reduction theory of rough sets was proposed. Firstly, the phase space of multivariate time series was originally reconstructed by a classical reconstruction technology. Then, the original decision-table of rough set theory was set up according to the embedding dimensions and time-delays of the original reconstruction phase space, and the rough set reduction was used to delete the redundant dimensions and irrelevant variables and to reconstruct the generic phase space. Finally, the input vectors for the prediction of multivariate time series were extracted according to generic reconstruction results to identify the parameters of prediction model. Verification results show that the developed reconstruction method leads to better generalization ability for the prediction model and it is feasible and worthwhile for application.
