J. Cent. South Univ. (2012) 19: 2554-2560
DOI: 10.1007/s11771-012-1310-0![]()
A novel adaptive mutative scale optimization algorithm based on chaos genetic method and its optimization efficiency evaluation
WANG He-jun(王禾军)1, E Jia-qiang(鄂加强)2, DENG Fei-qi(邓飞其)1
1. School of Automation Science and Engineering, South China University of Technology, Guangzhou 510640, China;
2. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract:
By combing the properties of chaos optimization method and genetic algorithm, an adaptive mutative scale chaos genetic algorithm (AMSCGA) was proposed by using one-dimensional iterative chaotic self-map with infinite collapses within the finite region of [-1, 1]. Some measures in the optimization algorithm, such as adjusting the searching space of optimized variables continuously by using adaptive mutative scale method and making the most circle time as its control guideline, were taken to ensure its speediness and veracity in seeking the optimization process. The calculation examples about three testing functions reveal that AMSCGA has both high searching speed and high precision. Furthermore, the average truncated generations, the distribution entropy of truncated generations and the ratio of average inertia generations were used to evaluate the optimization efficiency of AMSCGA quantificationally. It is shown that the optimization efficiency of AMSCGA is higher than that of genetic algorithm.
Key words:
chaos genetic optimization algorithm; chaos; genetic algorithm; optimization efficiency;
1 Introduction
Genetic algorithm (GA) was introduced firstly by Professor John Holland in University of Michigan in USA. By simulating the evolution of life in nature, GA does random search with guidance rather than blindness and is adapted to solve complex targeted nonlinear inverse problem in manual system [1]. And GA was applied to the research of function optimization firstly. The research works showed that genetic algorithm is an effective method when solving mathematical programming. But as for large and complex systems, especially solving nonlinear optimization problems, GA still has many defects, such as being difficult to ensure the converge of the most global optimal solution, the loss of the best chromosome in group and degradation in the process of evolution [2-3]. To avoid these problems, a lot of works, such as adding new genetic operator, improving the control parameters and improving the structure of the algorithm [4-9] had been done, but there were still some problems such as guiding global searching blindly and randomly and trapping easily into local optimization [4-9].
Chaos variables seem to be messy changes, but they are of inherent regularity actually. Optimized searching can be used based on the randomness, ergodicity and regularity of chaos variables [10-11]. And the basic idea can be expressed as mapping chaotic variables linear to the ranges of optimization variables, and then using chaos variables to search. However, as for a large space and multi-variable optimization searching, there are problems such as consuming long time computation and obtaining suboptimal solutions [10-11]. By integrating fully the advantages of chaos searching and genetic algorithm, some better optimization results were gotten by using the memory features of genetic algorithm and contemporary optimization solution to guide chaotic searching [12-14]. But the chaos variables from logistic model are limited by collapse number, and the obtained ergodicity of chaotic variables needs to be further improved. Therefore, the self-map with infinite collapse number [15] can be used to integrate the advantages of chaotic search and genetic algorithm fully and guide chaotic search by using the memory features of genetic algorithm and contemporary optimal solution. The searching space of optimization variables was changed by using self-map with infinite collapse number in a limited area and self-adaptive variable metric method. The searching accuracy was improved continuously to solve the slow convergence speed in searching for optimal value, and then the adaptive mutative scale chaos optimization algorithm (AMSCGOA) was presented. AMSCGOA not only has good searching direction, but also makes full use of the ergodicity of chaos and diversity of genetic to obtain high convergence speed and strong search capability. The results also show that the algorithm is of better convergence and search efficiency.
At present, various genetic operators for solving different types of questions were already put forward. How to reasonably choose these operators and its control parameter becomes the key point of using genetic algorithm to solve practical problems. Therefore, average truncated generations, distribution entropy of truncated generations and ratio of average inertia generations were used to evaluate the optimization efficiency of AMSCGOA. Compared with the optimization efficiency of genetic algorithm, the optimization efficiency of AMSCGOA is higher than that of genetic algorithm.
2 Adaptive mutative scale chaos genetic algorithm (AMSCGA)
2.1 Choice of chaos model
One-dimensional chaotic self-map can be expressed as [15]
xn+1=f (xn) (1)
There always are linear or nonlinear collapse phenomena in phase-space of chaos process, or else there is not chaos. In a sense, the Lyapunov index which is used to describe model “chaos” can also be seen as an indication of the average collapse times of the model. When absolute value of the average slope of the model is greater than 1, Lyapunov index is positive. Generally, the mapping collapse times of the commonly used Logistic model, Tent model and Chebyshev model are limited, but the chaotic sequence which they produced has good chaos.
Investigate the one-dimensional self-map defined by Eq. (2):
![]() (2)
(2)
With infinite collapse times, the map has infinite fixed points and zero points in the interval of [-1, 1]. Therefore, if we want to create chaos from this map, we must note the following conditions: 1) The initial value of iteration can not be zero; 2) Initial value can not be taken as any one of infinite fixed points, or it will be a stable orbit and can not produce chaos. The fixed point is the solution of xn+1=sin(2/xn).
It is easy to get transcendental number 2/(kπ) and transcendental equation x=sin(2/x), so its solution will also be transcendental number. In the actual engineering application, it is impossible to have transcendental numbers, but they are always approximated to be rational with limited accuracy. Therefore, as long as the initial value is not zero, chaos will occur. At that time, the domain of the map is [-1, 1], x≠0 and it does not include all the above transcendental points. The stochastic, sensitivity to initial value and ergodicity of the one- dimensional self-map xn+1=sin(2/xn) after 1 000 iteration are shown in Fig. 1. The initial value of Fig. 1(a) is x1=0.260 0 and the system output is irregular; the initial values of Fig. 1(b) are x1=0.260 1 and y1=0.260 2, ordinate is xn-yn, and we can see that the output of the two systems is completely different; the initial values of system Fig. 1(c) are x1=0.260 1 and y1=0.163 2, abscissa is xn (xn+1=sin(2/xn)) and ordinate is yn (yn+1=sin(2/yn)).
From Fig. 1, it is shown that results of the system will spread all over root spaces after iterating sufficient large times.
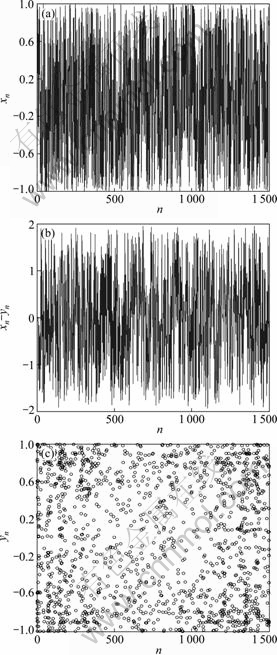
Fig. 1 Properties of stochastic, sensitivity to initial value and ergodicity of one-dimensional self-map xn+1=sin(2/xn): (a) x1=0.260 0; (b) x1 =0.260 1, y1=0.260 2; (c) x1=0.260 1, y1=0.163 2
Lyapunov index is an important indicator of measuring the nature of chaos. The Lyapunov index of chaotic self-map can be expressed as
![]() (3)
(3)
Compared to the commonly used finite collapse number map, the chaotic nature of Lyapunov index in Eq. (3) is more evident.
The stochastic, ergodicity and regularity of chaotic variables generated through model formula can be optimized. The basic idea is mapping the chaotic variables linearly to the value ranges of optimization variables, and then searching with the chaos variables. Chaotic searches based on different chaotic models are compared to evaluate the chaos characteristic. Calculate Eq. (4):
![]() (4)
(4)
where the minimized value of f(x) at the extreme point x=1 is zero.
Using the model of Eq. (2) and the Logistic model to do chaos optimization to the chaotic variables traversing the entire range (only for a search), and the obtained result is presented in Table 1. It is seen from Table 1 that the chaotic optimization result of Eq. (2) model is better, and it is also proved that compared to commonly used limited collapse number model, this model has more obvious chaotic features.
Table 1 Calculating results by comparing chaos map xn+1=sin(2/xn) to Logistic map

2.2 Construction of adaptive mutative scale chaos genetic algorithm (AMSCGA)
The genetic algorithm sometimes will fall into part extreme point, while the chaotic optimizing search process can avoid falling into part extreme point. Thus, this work will combine both of them, using an unlimited collapse number model xn+1=sin(2/xn) to propose an adaptive mutative scale chaos genetic algorithm. AMSCGA is divided into two parts. The coarse search uses the approach quantum genetic algorithms and similar carrying wave to give the initial value to chromosome, while careful search uses the second carrying wave to do chaotic careful search near the relative optimal solution.
Concrete algorithm steps are as follows:
1) Coarse searching
Step 1: Generating population chaotic variables
If we consider the solution of r-dimensional continuous space optimization problem as the points or vectors of r-dimensional space, the continuous optimization problem can be expressed as
![]()
![]() (5)
(5)
where r is optimization variable number.
A group of random numbers x1, x2, …, xr are generated in the range of (0, 1). Take the random number r as the initial value, then substitute it into the model with infinite collapse numbers xn+1=sin(2/xn) and produce r group chaotic variables: ti. The length of each chaotic variable group is N and N is the population size of genetic algorithm. Save the last value of all chaotic variables to store into vector Z0, Z0=(z1, z2,…, zr), and z1=x1N, z2=x2N, …, zr=xrN are the initial values of chaotic variables in careful search.
Step 2: Encoding
Use the r group chaotic variables to initialize group of the first generation of chromosomes. For example, the initialized result of the j-chromosome is
![]() (6)
(6)
Each chromosome is encoded by using of real place, avoiding inconvenience caused by the complex encoding and decoding of binary system. Chaotic variables extend the ergodicity of the solution space, which would speed up the search process and improve the probability of obtaining the global optimal.
Step 3: Solution space transformation
Each chromosome in group is mapped by linear transformation from ergodic space to solution space of function optimization. Therefore, each probability amplitude of chromosome corresponds to an optimization variable of solution space:
![]() (7)
(7)
To ensure that the new scope will not jump over border, we make the following deal: If ![]() , then
, then ![]() ; If
; If ![]() , then
, then ![]() .
.
Step 4: Fitness calculation
The objective function shown in Eq. (5) is fitness function to calculate the fitness of each chromosome and sort, then the best chromosome of past dynasties P0 and the best chromosome at the present age ![]() are recorded. If fit(
are recorded. If fit(![]() )> fit(P0), then P0=
)> fit(P0), then P0=![]() .
.
Step 5: Truncated condition judgment of algorithm
If truncated condition is satisfied, the algorithm is over and the current optimal solution X is saved, otherwise, evolve generation increase continuous algorithm.
2) Careful searching
If the obtained P0 of several generations through rough search remains constant, then it enters into the fine search stage. The sequence Zi is produced by Z0 in the assignment stage. According to Eq. (2), each element of vector continues down to produce the chaotic sequences.
Step 1: Creating searching variables:
![]() (8)
(8)
In this equation ηi is self-adaptive adjust regulation and self-adaptation can be determined by
![]() (9)
(9)
where m is an integer determined by the optimum objective function. In this work, m = 2.
Because during the initial careful iteration search, (x1, x2, …, xn) changes largely and needs larger ηi. As the search goes on and gradually gets close to the optimal point, it needs to use smaller ηi in order to do search in the smaller scale (![]() ).
).
Step 2: Use the objective function to evaluate ![]() and calculate the corresponding
and calculate the corresponding ![]() . If
. If ![]() > f(X), then f(X)=
> f(X), then f(X)=![]() , or give up
, or give up ![]() .
.
Step 3: If the condition meets the cut-off judge evidence, the search is ended and the optimal solution X is output, otherwise it is necessary to return to Step 1.
2.3 Application of adaptive mutative scale chaos genetic algorithm (AMSCGA)
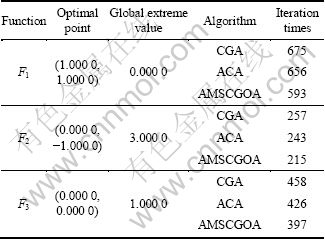
The AMSCGA was used to optimize the following three test functions. Compared with chaotic genetic algorithm (CGA) [12] and adaptive mutative scale chaos optimization algorithm [15], the results are given in Table 2. Obviously, the AMSCGA is an effective method to solve optimization problems.
![]() (10)
(10)
![]()
![]()
![]() (11)
(11)
![]() (12)
(12)
where F3 seeks for the global maximum, and others seek for the global minimum.
Table 2 Results of comparing algorithm proposed to algorithms in Refs. [5, 12]
3 Optimization efficiency evaluation of adaptive mutative scale chaos genetic algorithm
3.1 Analysis parameters of optimization efficiency
In order to quantitatively analyze the searching performance of AMSCGA, in addition to the two parameters of “average truncated generation” and “truncated generation distribution entropy” [16], the parameter average inert generation is defined to describe the chaotic search process more clearly.
Definition 1: Truncated generations
Generally, engineering optimization problem is to solve the extreme value of n function f(X) in the constraint region D, namely maxf(x). In the searching process, when f(x) reaches the calculation accuracy ε in the feasible domain D for the first time (ε, fmax, ε is the pre-set extreme minimum positive number), the iteration number ε is called truncated generation. If it reaches predetermined maximum iteration number Kmax and still does not reach the searching precision, truncated generations is ruled as Kmax.
Definition 2: Average truncated generations
N is the number of independent operation, Ti is the i-th truncated generation when independently being run,
and ![]()
![]() Element T ranks according to the order from small to large and gets a new set,
Element T ranks according to the order from small to large and gets a new set, ![]()
![]()
![]() ,
,![]()
![]() Here, Ci is the statistical frequency number corresponding to
Here, Ci is the statistical frequency number corresponding to ![]() and statistical frequency time
and statistical frequency time ![]()
![]() i=1, 2, …, M} is calculated, then when the search method achieves the calculate accuracy ε, the average truncated generations is defined as
i=1, 2, …, M} is calculated, then when the search method achieves the calculate accuracy ε, the average truncated generations is defined as
![]() (13)
(13)
Definition 3: Distribution entropy of truncated generations
When genetic algorithm achieves calculate accuracy, under the strategy S, the distribution entropy of truncated generations is defined as
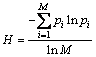 (14)
(14)
Definition 4: Inert generation rate
Before the truncated generations searching, if the optimal value of the K+r (and r≥1) is the same as that of the K (fK+r=fK), and the optimal value of the K+r+1 changes (fK+r<>K), it is shown that between the K→K+r iterations the optimal value has not improved, the interval K→K+r is named as inertia interval, and r is named as inert generation. And there are totally m inert intervals and each interval’s inert generation is ri (i=1, 2, …, m). So, before the truncated generation searching, the ratio of the sum of each inertia interval to truncated generation is defined as inertia generation rate R:
![]() (15)
(15)
Definition 5: Average inertia generation ratio
When the number of independent running is N, the definition of the average inert generation ratio Rm is the weighted average value of each inertia generation rate when running independently, namely:
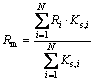 (16)
(16)
The average truncated generation and truncated generation distribution entropy are respectively used to measure the convergence speed and convergence instability of several independent running optimization algorithms. If the average cut-off generation is smaller, the searching time of optimal algorithm is smaller, time is shorter and convergence speed is faster. If the cut-off generation distribution entropy is smaller, several independent running truncated generations are concentrated closely, convergence stability is better and optimal algorithm is less sensitive to initial values. Average inertia generation rate reflects the ratio of inertia interval to inertia generation in the searching process. The larger the ratio of average inertia generation is, the more the iteration times that do not have optimal objective function value in the searching process are and the lower the algorithm efficiency is.
3.2 Analysis and evaluation of optimization efficiency
To judge the effectiveness of adaptive mutative scale chaos genetic algorithm, the optimization efficiency of genetic algorithm is compared. Solving the maximum value of the function shown in Eq. (17) is taken as an example to do research on the algorithm property of different parameters:
![]()
![]() (17)
(17)
Obviously, optimal value of the function is f(3, 1)=10. The size of precision ε can be easily controlled and the function introduces two non-linear terms which can test the nonlinear optimization of chaotic genetic algorithm.
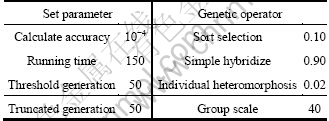
The set parameters and genetic operators used in two methods are given in Table 3.
Table 3 Value of functioning parameters
As for impact on optimization efficiency, selection and hybridization are greater than heteromorphosis, which is used as assisted operator of genetic algorithm. Therefore, the ranking selection and simple heteromorphosis operator are only discussed. In order to judge the effectiveness of AMSCGA, optimization efficiency of AMSCGA is compared with the optimization efficiency of genetic algorithm.
1) Ranking selection
The hybridization probability is 0.9 and hetero- morphosis probability is 0.02. The value range of the best individual ranking selection probabilities is from 0.04 to 0.22, interval is 0.02 and there are totally 10 values. Numbers are successively from 1 to 10. Each value separately runs for 150 times, and (T, H, Rm) three-dimensional relationship is shown in Fig. 2.
Figure 2 shows that, as ranking selection probability increases, whether adaptive mutative scale chaotic genetic algorithm or genetic algorithm, their average truncated generation T, truncated generation distribution entropy H and average inertia generation ratio Rm decrease first and then increase, which fully shows that the optimization efficiency of adaptive mutative scale chaos genetic algorithm and genetic algorithm increase first and then decrease. However, the average truncated generation T, truncated generation distribution entropy H and average inertia generation ratio Rm of AMSCGA are smaller than those of genetic algorithm (GA). Apparently, the optimization of AMSCGA is more efficient than that of GA.
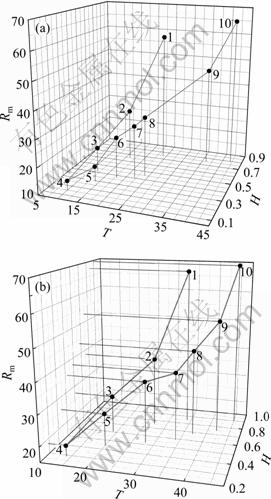
Fig. 2 Optimization efficiency of different rank selection operators: (a) Adaptive mutative scale chaos genetic algorithm; (b) Genetic algorithm
2) Simple hybridization
The ranking selection probability is 0.1, hetero- morphosis probability is 0.02 and value range of hetero- morphosis probability is from 0.78 to 0.96. There are totally 10 values. Numbers are successively from 1 to 10. Each value separately runs for 150 times and (T, H, Rm) three-dimensional relationship is shown in Fig. 3.
Figure 3 shows that, as hybridization probability increases, whether for AMSCGA or GA, their average truncated generation T, truncated generation distribution entropy H and average inertia generation ratio Rm decrease first and then increase, which fully shows that the optimization efficiency of adaptive mutative scale chaos genetic algorithm and genetic algorithm increase first and then decrease. However, the average truncated generation T, truncated generation distribution entropy H and average inertia generation ratio Rm of AMSCGA are smaller than those of GA. Apparently, the optimization efficiency of AMSCGA is higher than that of GA.
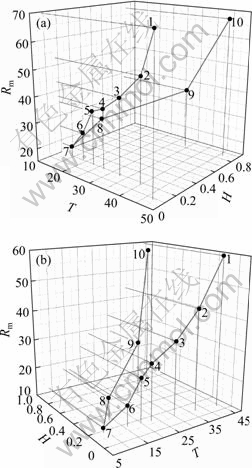
Fig. 3 Optimization efficiency of different brief crossover operators: (a) Adaptive mutative scale chaos genetic algorithm; (b) Genetic algorithm
4 Conclusions
1) Ergodicity in chaotic variable constraint interval generated from chaotic model with infinite collapse time is better than chaotic model with finite collapse time of chaotic variables (such as Logistic model), which also shows that the chaotic characteristics of this model is more evident.
2) By combing chaos theory with genetic algorithm and using chaotic variables produced by the chaotic model with infinite collapse times, a new optimization algorithm, adaptive mutative scale chaotic genetic algorithm, is proposed, which is different from the traditional encoding pattern that uses real number coding, overcomes the frequent encoding and decoding process between binary system and decimal system and enhances arithmetic convergence stability. It greatly improves the search ability of algorithm. Through the test of typical function, the result shows that the algorithm is simple and practical which does not require continuity and differentiability to the optimization problem and programming is convenient. It is an effective method to solve the optimization problem.
3) Taking the average truncated generation, truncated generation distribution entropy and average inertia generation ratio as the evaluation indexes, the optimization efficiency of AMSCGA is evaluated. The results show that the optimization efficiency of AMSCGA is higher than that of GA.
References
[1] YAO Jun-feng, MEI Chi, PENG Xiao-qi. The application research of the chaos genetic algorithm (CGA) and its evaluation of optimization efficiency [J]. Acta Automatica Sinica, 2002, 28(6): 935-942. (in Chinese)
[2] WEILE D S, MICHIELSSEN E. The use of domain decomposition genetic algorithms exploiting model reduction for the design of frequency selective surfaces [J]. Computer Methods in Applied Mechanics and Engineering, 2000, 186(2/3/4): 439-458.
[3] RENNER G, EK?RT A. Genetic algorithms in computer aided design [J]. Computer-Aided Design, 2003, 35(8): 709-726.
[4] GOSSELIN L, TYE-GINGRAS M, MATHIEU-POTVIN F. Review of utilization of genetic algorithms in heat transfer problems [J]. International Journal of Heat and Mass Transfer, 2009, 52(9/10): 2169-2188.
[5] LOZANO M, HERRERA F, CANO J R. Replacement strategies to preserve useful diversity in steady-state genetic algorithms [J]. Information Sciences, 2008, 178(23): 4421-4433.
[6] SANTARELLI S, YU TIAN LI, GOLDBERG D E, ALTSHULER E, O’DONNELL T, SOUTHALL H, MAILLOUX R. Military antenna design using simple and competent genetic algorithms [J]. Mathematical and Computer Modelling, 2006, 43(9/10): 990-1022.
[7] KAVVADIAS N, GIANNAKOPOULOU V, NIKOLAIDIS S. Development of a customized processor architecture for accelerating genetic algorithms [J]. Microprocessors and Microsystems, 2007, 31(5): 347-359.
[8] KATAYAMA K, HIRABAYASHI H, NARIHISA H. Analysis of crossovers and selections in a coarse-grained parallel genetic algorithm [J]. Mathematical and Computer Modelling, 2003, 38(11/12/13): 1275-1282.
[9] RIPON K S N, KWONG S, MAN K F. A real-coding jumping gene genetic algorithm (RJGGA) for multiobjective optimization [J]. Information Sciences, 2007, 177(2): 632-654.
[10] LI Bing, JIANG Wei-sun. Chaotic optimization method and its applications [J]. Control Theory & Applications, 1997, 14(4): 613-615. (in Chinese)
[11] ZHANG Tong, WANG Hong-wei, WANG Zi-cai. Mutative scale chaotic optimization method and its applications [J]. Control and Decision, 1999, 14(3): 285-288. (in Chinese)
[12] GUO Yi-qiang, WU Yan-bin, JU Zheng-shan, WANG Jun, ZHAO Lu-yan. Remote sensing image classification by the chaos genetic algorithm in monitoring land use changes [J]. Mathematical and Computer Modelling, 2010, 51(11/12): 1408-1416.
[13] YANG Xiao-hua, YANG Zhi-feng, YIN Xin-an, LI Jian-qiang. Chaos gray-coded genetic algorithm and its application for pollution source identifications in convection–diffusion equation [J]. Communications in Nonlinear Science and Numerical Simulation, 2008, 13(8): 1676-1688. (in Chinese)
[14] GHAROONI-FARD G, MOEIN-DARBARI F, DELDARI H, MORVARIDI A. Scheduling of scientific workflows using a chaos-genetic algorithm [J]. Procedia Computer Science, 2010, 1(1): 1439-1448.
[15] E Jia-qiang, WANG Chun-hua, WANG Yao-nan, GONG Jin-ke. A new adaptive mutative scale chaos optimization algorithm and its application [J]. Journal of Control Theory & Applications, 2008, 6(2): 141-145.
[16] SUN Rui-xiang, QU Liang-sheng. Quantitative analysis on optimization efficiency of genetic algorithm [J]. Acta Automatica Sinica, 2000, 26(4): 552-556. (in Chinese)
(Edited by YANG Bing)
Foundation item: Project(60874114) supported by the National Natural Science Foundation of China
Received date: 2011-09-28; Accepted date: 2012-06-12
Corresponding author: WANG He-jun, PhD Candidate; Tel: +86-13829959995; E-mail: wanghj1974@126.com
Abstract: By combing the properties of chaos optimization method and genetic algorithm, an adaptive mutative scale chaos genetic algorithm (AMSCGA) was proposed by using one-dimensional iterative chaotic self-map with infinite collapses within the finite region of [-1, 1]. Some measures in the optimization algorithm, such as adjusting the searching space of optimized variables continuously by using adaptive mutative scale method and making the most circle time as its control guideline, were taken to ensure its speediness and veracity in seeking the optimization process. The calculation examples about three testing functions reveal that AMSCGA has both high searching speed and high precision. Furthermore, the average truncated generations, the distribution entropy of truncated generations and the ratio of average inertia generations were used to evaluate the optimization efficiency of AMSCGA quantificationally. It is shown that the optimization efficiency of AMSCGA is higher than that of genetic algorithm.


