
J. Cent. South Univ. (2018) 25: 1099-1106
DOI: https://doi.org/10.1007/s11771-018-3809-5
Neuron system shock superimposed response based on catastrophe dynamics
LI Bin(李斌), CHEN Chao(陈超), LI Tuo(李拓)
College of Economics and Trade, Hunan University, Changsha 410079, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract:
With the rapid development of computer science and artificial intelligence technology, the complexity and intelligence of the neural network models constructed by people have been greatly improved. When the complex neuron system is subjected to the impact of “catastrophic”, its original characteristics may be changed, and the consequences are difficult to predict. Catastrophe dynamics mainly studies the source of the sudden violent change of nature and human society and its evolution. The impact of the system can be divided into endogenous and exogenous shocks. In this article, catastrophe theory is used to study the neuron system. Based on the mean field model of Hurst and Sornette, introducing the weight parameters, mathematical models are constructed to study the response characteristics of the neuron system in face of exogenous shocks, endogenous shocks, and integrated shocks. The time characteristics of the shock response of the neuron system are discussed too, such as the instantaneous and long-term response of the system in face of shocks, the different response forms according to the weight or linear superposition, and the influence of adjusting parameters on the neuron system. The research result shows that the authoritarian coefficient and weight coefficient have a very important influence on the response of neuron system; By adjusting the two coefficients, the purpose of disaster prevention, self-healing protection and response reducing can be well achieved.
Key words:
neuron system; catastrophe dynamics; endogenous shock; exogenous shock; superimposed response;
Cite this article as:
LI Bin, CHEN Chao, LI Tuo. Neuron system shock superimposed response based on catastrophe dynamics [J]. Journal of Central South University, 2018, 25(5): 1099–1106.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-018-3809-51 Introduction
The neuron system is a highly complex nonlinear system, which has a very large number of neurons and complex neural network structure. The most basic task for neurons is to convert the external stimuli into neural coding information, process it and response to the results [1–5].At present, the research based on neural system has been developed into many fields, such as biology, physiology, physics, control science, computer science, artificial intelligence. People have established various forms of mathematical models, which are usually highly complex nonlinear dynamic systems, to describe the neuron system. HODGKIN et al [6] established the Hodgkin- Huxley (HH) neuron system model based on the ion channel theory, and used it to study the discharge characteristics and synchronization behavior of neurons. FITZHUGH [7] simplified the above model under certain conditions, and put forward the two-dimensional FHN neuron model. Many scholars further studied the characteristics of the FHN mode under different conditions, such as WIESENFELD et al [8], TUCKWELL et al [9], ACEBRON et al [10] and KITAJIMA et al [11]. Recently, many scholars have studied the neuron system based on noise excitation conditions. For instance, WANG [12] and YANG et al [13] studied the response and synchronization characteristics of FHN neuron system under noise excitation condition. ZHAO et al [14] studied the steady state probability distribution and mean first passage time of FHN neural system based on non-Gaussian noise excitation condition. In recent years, with the rapid development of computer science and artificial intelligence techniques, the neural network models built by people are becoming more and more complex, and the intelligent degree of the models is also significantly improved. On March 9, 2016, Google AlphaGo’s victory over South Korea’s top chess player Lee Sedol is a typical example. Scholars’ study on neuronal system is more and more close to the complex random network characteristics. For example, LI et al [15] thought that neuron system has the characteristics of small world networks, and studied the response and synchronization of small world neural network system under the influence of spatial correlated white noise.
On one hand, the development of neuron system provides useful help for the human society; on the other hand, it also raises concerns. When complex neuron system suffers the shock of “catastrophic” type, it will change the original characteristics, and the consequences are difficult to predict. In this paper, we study the shock response of neuron system on the basis of catastrophe dynamics theory, which has practical significance. Catastrophe refers to the extreme events in the process of the development of nature and human society [16], which has a crucial impact on the development of the nature and the human society. Catastrophe dynamics mainly studies the power source and evolution of sudden violent change in the nature and human society. The shocks of the system can be divided into exogenous and endogenous shocks [17, 18]. The power of endogenous shocks is derived from the internal system, which is the result of internal motion of the system. The shock can be expressed in an instant, or in a long term accumulation. Exogenous shocks are usually derived from accidental events that have a major impact on the system [19]. The research on the impact response of the neuron system is more inclined to the total amount and trend characteristics and the mean field model is consistent with the characteristics of complex neuron system [20]. Based on the mean field model of HURST [21] and SORNETTE et al [22–24], and introducing the weight parameters, mathematical models are constructed to study the response characteristics of the neuron system in face of exogenous shocks, endogenous shocks, and integrated shocks. The time characteristics of the shock response of the neuron system is discussed too, such as the instantaneous and long-term response of the system in face of shocks [25–27], the different response forms according to the weight or linear superposition, and the influence of adjusting parameters on the neuron system. The research shows that the authoritarian coefficient and weight coefficient have a very important influence on the response of neuron system; when the two coefficients are adjusted, the purpose of disaster prevention, self-healing protection and response reducing can be well achieved [28, 29]. The model can be also applied in other systems of human society, like real estate market [30].
2 Response of neuron system to multiple shocks
2.1 Response of neuron system to exogenous shocks
In order to study the burst superposition response of the neuron system, general theory of catastrophe dynamics is involved. SORNETTE et al [22–24] proposed a memory average field model A(t), as the response in the moment t to the noise accumulation η(τ) and the memory kernel function K(t–τ) expressed as:
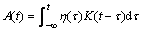 (1)
(1)
Assuming that the system is subjected to exogenous shocks at t=0, and the amplitude is A0, the mathematical expectation of the neuron system response to the exogenous shocks can be expressed as:
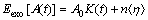 (2)
(2)
Considering the general superposition of the internal perturbation and the external impact, the parameters α and β can be introduced, and the weight of interaction can be normalized, so α+β=1. Assume that the neuron system is subjected to exogenous shock at t=0, and the amplitude is A0. As mentioned before, the total perturbation of the system is the superposition of internal perturbation and external shocks, we change a superposition method to add the internal perturbation and external impact by different weights to study the role of different perturbation in the total perturbation. The total perturbation is:
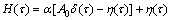 (3)
(3)
where the parameter α represents the weight of external shocks in the total perturbation, and 0≤α≤1. When the parameter α takes the minimum value of 0, the total perturbation is η(τ), which means that there is no exogenous shock; when the maximum value is 1, the total perturbation is A0δ(τ), which means that there is no internal perturbation. If calling the state of the two extreme values “dictatorship”, when α=0, the system is in a dictatorship η(τ); when α=1, the system is in a dictatorship A0δ(τ). Then recalculate the mathematical expectation of the response of the system to exogenous shocks:
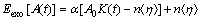 (4)
(4)
After the introduction of authoritarian coefficient α, when neuron system under external shock at t=0, the total perturbation caused by the impact is determined not only by the shock function itself but also by coefficient α, which makes the expected function variable.
The structural characteristics of the system is directly related to its integrated response to impact and some adjustments can be made to the neuron system by changing the authoritarian coefficient α when system is in face of external shock. The multi-fractal random walk model (MRW) proposed by SORNETTE et al [22–26] can be introduced to study the stability of neuronal system.
Supposing that neuron system is subjected to an endogenous shock with a strength of ω0 at t=0, the shock can be represented as ω0δ(τ). With linear superposition method, the perturbation for the total system is η(τ)+ω0δ(τ), then:
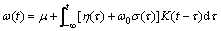 (5)
(5)
The mathematical expectation of conditional volatility is:
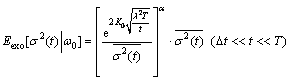 (6)
(6)
Due to the fact that exogenous shocks will decay to zero, it can be showed as:
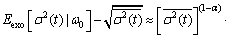
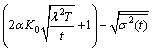 (7)
(7)
2.2 Response of neuron system to integrated shocks
In the case of single shock, authoritarian coefficient α has taken to extreme, and no longer become a variable that affects the response of the neuron system. But from another point of view, the responses of endogenous and exogenous shocks are different. So, if the system is influenced by the integrated impact of endogenous and exogenous shocks, the overall response of the system can be controlled by changing proportional form of the endogenous and exogenous shocks.
Illustrate this problem further: exogenous shocks lead to internal fluctuations of neuron system,which leads to endogenous shocks, and then the two kinds of impact work synthetically. For simplicity, suppose that the neuron system is impacted by exogenous shock A0 at t=0, and comprehensively impacted by endogenous shock B0 at 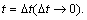 In this situation, the major shock of neuron system comes from the stacking impact of endogenous and exogenous shocks, then Eexo[A(t)]=A0K(t)+n<η>, the response function of endogenous shocks is: E[B(t)|Y=B0]=
In this situation, the major shock of neuron system comes from the stacking impact of endogenous and exogenous shocks, then Eexo[A(t)]=A0K(t)+n<η>, the response function of endogenous shocks is: E[B(t)|Y=B0]=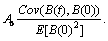 Because
Because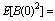
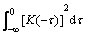 is constant, set it as 1/k. The endogenous impulse response function can be expressed as:
is constant, set it as 1/k. The endogenous impulse response function can be expressed as:
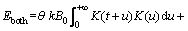
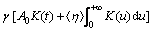 (8)
(8)
As the same, θ+τ=1 where θ represents the weight of the response of the neuron system to the endogenous shocks in the total response, and τ represents the weight of the response of the neuron system to the exogenous shocks in the total response. When τ=0, Eboth is degenerated into Eendo. When τ=1, Eboth is degenerated into Eexo. Calling τ “the weight coefficient”, the formula above can be expressed as:

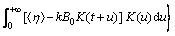 (9)
(9)
Using the calculation results of formula above, we get:
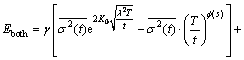
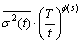
 (10)
(10)
If in the longer period of time, τ is small, Maclaurin series can be used to expand and approximate above formula and we get:
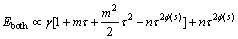 (11)
(11)
Because φ(s) is proportional to s, and 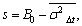 in other words, any s corresponds a response size of the shock. When φ(s)>>1, the response of neuron system can be approximated as:
in other words, any s corresponds a response size of the shock. When φ(s)>>1, the response of neuron system can be approximated as:
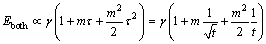 (12)
(12)
At this time, the response is mainly determined by the exogenous response, the size of the weight coefficient τ is linearly related to the total response of the system. When φ(s)<<1, the response is mainly determined by the endogenous response, the response of neuron system can be approximated as:
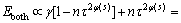
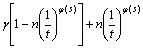 (13)
(13)
In addition, when φ(s) is approaching 1/2, the response of neuron system can be approximated as:
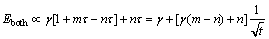 (14)
(14)
where τ is the time coefficient of the response of the neuron system, and the response function has the simplest form.
3 Time characteristics of neuron system to shock response
3.1 Transient response of neuron system to shocks
In the theory of catastrophe dynamics, in the case of the impact occurring in a short time after t=0, (attenuation power law in a short period of time after the shock occurred), take formula (2) into Taylor expansion:
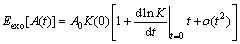 (15)
(15)
Substitute this to formula above:
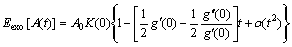 (16)
(16)
Then do the first order Taylor expansion in the vicinity of t=0:
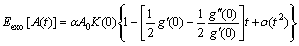 (17)
(17)
3.2 Gradual long-term response of neuron system to shocks
The above discussion about the form of the memory kernel function K(t) shows that it is a monotone decreasing function. For any u≥0, we have K(t+u)≤K(t). In addition, if the attenuation speed of K(t) is faster than 1/t, namely
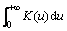
 exists, there is:
exists, there is:
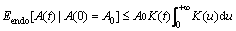 (18)
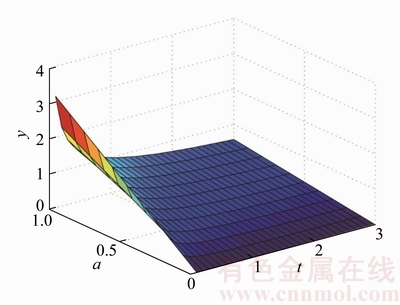
(18)
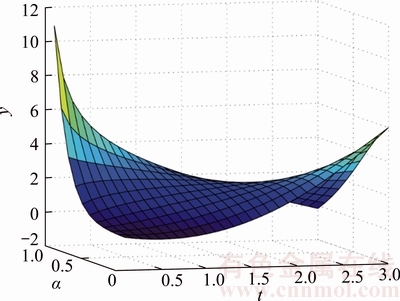
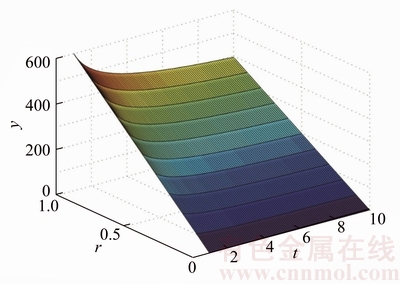
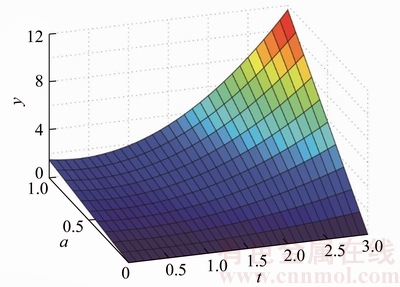
So, for any constant C, while K(t) But this condition may not be significant. For example, for a memory kernel function K(t)∝1/t1+θ (θ>0), the conditional noise and impact are very similar, leading to [19]: This causes that there is almost no difference between the attenuation form of endogenous and exogenous shocks. By contrast, if the attenuation speed of the memory kernel function K(t)∝1/t1+θ (θ>0) is slower than 1/t, then: In this condition, the attenuation speed of the endogenous impact will become slower than the exogenous impact. Therefore, 1/t will be a demarcation point between them in a long term. Formula (2) is used in the above analysis of an exogenous shock. If using formula (4), according to the memory kernel function K(t)∝1/t1+θ (θ>0), then: For the memory kernel function K(t)∝1/t1+θ (θ>0), there is: 4 Simulation analysis In order to verify the correctness of the above mathematical analysis, and further analyze the response of the neuron system to various shocks, the main results are analyzed by mathematical simulation. On the basis of the parameter setting of correlation function, the influence of the coefficient of dictatorship α and the weight coefficient γ on the system are analyzed when the neuron system is subjected to the corresponding impact. Figure 1 is based on the calculation result of formula (7) which is the analysis of the simulation of the external shock response. The simulation results show that the smaller α can effectively restrain the response of the system when t is small, and the larger α restrains the response when t is larger, which is consistent with our expectation. That is to say, α should be minimized in the early stage of the impact of the neuron system, and α should be increased in the late stage. That is, in the initial stage of the impact, effective measures should be carried out to reduce the impact of infection. When the impact effect is declining, the external force should be added to strengthen the impact force, which can weaken the impact of the whole. Figure 1 Exogenous shock response simulation ( Figures 2 and 3 show the response of the system under the integrated shock (corresponding to formula (12) and formula (14)), which represent the standard response form and the simplified response form. Through the analysis of the simulation results, it can be found that the weight coefficient is positively correlated with the response of the system. The results show that the larger the proportion of exogenous shocks is, the more unstable the system is. This shows that to ensure the stability of the neuron system, the proportion of endogenous shocks must be increased. That is to say, when the neuron system is subjected to integrated impact, it is necessary to form a response mechanism in itself, which can reduce the shock response of the system by increasing the intensity of the internal fluctuations to suppress the impact of exogenous shocks. Figure 2 Integrated shock response simulation Figure 3 Integrated shock response simulation Figure 4 shows the simulation of the transient response of the system subjected to impact (corresponding to formula (17)). Figure 5 shows a simulation of the long-term response of the system under shock (corresponding to formula (23)). Through Figure 4, it is found that the transient response is similar to that of the previous analysis after adding the dictatorship coefficient. Dictatorship coefficients appear as the coefficients of the response function, that is to say, in this case the dictatorship coefficient has a linear effect on the neuron system. The dictatorship coefficient α instantly begins to play a role when the external impact occurs, affecting the degree that the neuron system responses to the shock. When α increases, the transient response of the neuron system also increases in equal proportion. If we can reduce the weight of α, the peak response of the neuron system will be reduced. That is to say, the anti-shock ability of the neuron system is inversely proportional to the magnitude of α in the instantaneous action, but this has no direct effect on the attenuation rate of the response. That also further confirms the significance of studying the external parameter α, influencing or controlling α. Figure 4 Instantaneous response simulation Seen from Figure 5, the impact forms of superposition have almost no great impact on the attenuation situation of the response. Due to the self-recovery ability of the neural system, when the system is subjected to a self-recovery range shock, in a long period of time, the neuron system can be restored to normal by its own function. That is to say, when influencing and improving the system’s superposition approach in face of shocks, the main changes are the response intensity and the overall amount of shock. There has a relatively small impact on the long-term recovery process of the system. Figure 5 Long-term response simulation 5 Conclusions The main thrust of this work is to use catastrophe dynamics method to research the response of the neuron system to the superposition of the endogenous and exogenous shock. According to the research, the two parameters, authoritarian coefficient α and weight coefficient γ, do have a crucial impact on the system response in the case that neuron system can be influenced or controlled. If the parameters’ numerical size can be interfered or adjusted, the result will have a significant impact on the neuron system’s response. When the two coefficients are adjusted, the purpose of disaster prevention, self-healing protection and response reducing can be well achieved. In the same way, the model can be applied to the study of the other systems’ response of disaster impact in nature and human’s society, like the financial market. References [1] KOCH C, SEGEY I. Methods in neuronal modeling: From ions to networks [M]. Cambridge: MIT Press, 1998: 50–55. [2] DAYAN P, ABBOTT L. Theoretical neuroscience: Computational and mathematical modeling of neural systems (computational neuroscience) [M]. Cambridge: MIT Press, 2002: 154–155. [3] SCHAAL S. The handbook of brain theory and neural networks [J]. Inorganica Chimica Acta, 2002, 82(1): 69–74. [4] RABINOVICH M L, VARONA P, SELVERSTON A L. Dynamical principles in neuroscience [J]. Reviews of Modem Physics, 2006, 78(4): 1213–1265. [5] KANDEL E R, SCHWARTZ J H, JESSELL T M. Principles of neural science [M]. 4th edition. Wiley, 2001. [6] HODGKIN A L, HUXLEY A F. A quantitative description of membrane current and its applications to conduction and excitation in nerve [J]. Bulletin of Mathematical Biology, 1990, 52(1, 2): 25–71. [7] FITZHUGH R. Thresholds and plateaus in the Hodgkin- Huxley nerve equations [J]. Journal of General Physiology, 1960, 43(5): 867–896. [8] WIESENFELD K, PIERSON D, PANTAZELOU E. Stochastic resonance on a circle [J]. Physical Review Letters, 1994, 77(72): 2125–2129. [9] TUCKWELL H C, RODRGUEZ R, WAN F Y M. Determination of firing times for the stochastic Fitzhugh-Nagumo neuronal model [J]. Neural Computation, 2003, 15(1): 143–159. [10] ACEBRON J A, BULSARA A R, RAPPEL W J. Noisy Fitzhugh-Nagumo model: From single elements to globally coupled networks [J]. Physical Review E, 2004, 69(2): 026202. [11] KITAJIMA H, KURTHS J. Synchronized firing of FitzHugh–Nagumo neurons by noise [J]. Chaos An Interdisciplinary Journal of Nonlinear Science, 2005, 15(2): 23704. [12] WANG Bao-yan. Synchronization of coupled FHN neurons under noise [J]. Journal of Xi’an Polytechnic University, 2011, 25(2): 232–238. (in Chinese) [13] YANG Ya-qiang, WANG Can-jun. Steady state characteries of Fitzhugh-Nagumo neural system subjected to two different kinds of colored noises [J]. Acta Physica Sinica, 2012, 61(12): 120507. [14] ZHAO Yan, XU Wei, ZOU Shao-cun. The steady state probability distribution and mean first passage time of FHN neural system driven by non-Gaussian noise [J]. Acta Physica Sinica, 2009, 58(3): 1396–1402. [15] LI Na, YANG Xiao-li. Synchronous dynamics of small-world neuronal network system with spatially correlated white noise [J]. Acta Physica Sinica, 2015, 64(22): 86–94. (in Chinese) [16] SORIIETTE D. Complexity, catastrophe and physics [J]. Physics World, 2015, 12(12): 57. [17] MENEZES M A, BARABASI A L. Fluctuations in network dynamics [J]. Phys Rev Lett, 2004, 92(2): 028701. [18] HELMSTETTER A, SORNETTE D, GRASSO J. Mainshocks are aftershocks of conditional foreshocks: How do foreshock statistical properties emerge from aftershock laws [J]. Journal of Geophysical Research Solid Earth, 2002, 108(B1): 20–24. [19] SORNETTE D, HELMSTETTER A. Endogenous versus exogenous shocks in systems with memory [J]. Physica A: Statistical Mechanics & its Applications, 2003, 318(3, 4): 577–591. [20] MANDELBROT B B, NESS J W V. Fractional brownian motions, fractional noises and applications [J]. Siam Review, 1968, 10(4): 422–437. [21] HURST H. Long term storage capacities of reservoirs [J]. Transactions of the American Society of Civil Engineers, 1951, 116(12): 776–808. [22] SORNETTE D, MALEVERGNE Y, MUZY J F. What causes crashes? [J]. Risk, 2003, 16(2): 67–71. [23] SORNETTE D, ZHOU W X. Importance of positive feedbacks and overconfidence in a self-fulfilling Ising model of financial markets [J]. Physica A: Statistical Mechanics & Its Applications, 2005, 370(2): 704–726. [24] HELMSTETTER A, SORNETTE D. Subcritical and supercritical regimes in epidemic models of earthquake aftershocks [J]. Journal of Geophysical Research Solid Earth, 2002, 107(B10): ESE10. [25] HUI Q, HADDAD W M, BAILEY J M. A stochastic mean field model for an excitatory and inhibitory synaptic drive cortical neuronal network [J]. IEEE Transactions on Neural Networks & Learning Systems, 2014, 25(4): 751–763. [26] DI V M, BURIONI R, CASARTELLI M. Neural networks with excitatory and inhibitory components: Direct and inverse problems by a mean-field approach [J]. Physical Review E, 2015, 93(1): 012305. [27] ARGOLLOD M M, BARABASI A L. Separating internal and external dynamics of complex systems [J]. Physical Review Letters, 2004, 93(6): 068701. [28] LIU An-feng, LIU Xiao, LI He. MDMA: A multi-data and multi-ACK verified selective forwarding attack detection scheme in WSNs [J]. IEICE Transactions on Information and Systems, 2016, 99(8): 2010–2018. [29] POLO V, ANDRES J, BERSKI S. Understanding reaction mechanisms in organic chemistry from catastrophe theory applied to the electron localization function topology [J]. Journal of Physical Chemistry A, 2008, 112(31): 7128–7136. [30] BELEJ M. Catastrophe theory in explaining price dynamics on the real estate market [J]. Real Estate Management and Valuation, 2013, 21(3): 51–61. (Edited by YANG Hua) 中文导读 基于灾变动力学的神经元系统冲击叠加响应 摘要:随着计算机科学和人工智能技术的飞速发展,人们构建的神经网络模型的复杂性和智能性得到了极大的提高。当复杂的神经元系统受到“灾变性”的冲击时,其原有特征可能发生变化,后果难以预测。灾变动力学主要研究自然和人类社会突发剧烈变化的根源及其演变。系统所受到的冲击可分为内生冲击和外生冲击。本文在神经元系统通用理论模型的基础上,引入灾变动力学理论展开了研究。基于平均场模型,引入权重系数,建立起数学模型研究神经元系统在面临外生冲击、内生冲击、叠加冲击时的响应特性,并进一步讨论了神经元系统冲击响应的时间特性,如系统面临冲击的瞬时和长期响应,按权重或线性叠加时不同的响应形式,以及调节参数对神经元系统的影响。研究表明,独裁系数和权重系数对神经元系统的响应有着非常重要的影响,对这两个系数进行调整,能很好地实现防灾、自愈保护和减轻灾害的目的。 关键词:神经元系统;灾变动力学;内生冲击;外生冲击;叠加响应 Foundation item: Project(CX2016B142) supported by the Hunan Provincial Innovation Foundation for Postgraduate, China Received date: 2017-07-20; Accepted date: 2017-10-30 Corresponding author: CHEN Chao, PhD; Tel: +86–13755169705; E-mail: 13252570@qq.com; ORCID: 0000-0002-9939-7575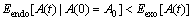 (19)
(19)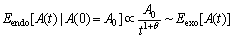 (20)
(20)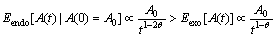 (21)
(21)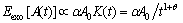 (22)
(22)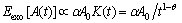 (23)
(23)

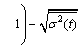 )
)

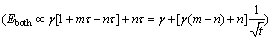
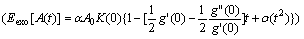
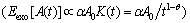
Abstract: With the rapid development of computer science and artificial intelligence technology, the complexity and intelligence of the neural network models constructed by people have been greatly improved. When the complex neuron system is subjected to the impact of “catastrophic”, its original characteristics may be changed, and the consequences are difficult to predict. Catastrophe dynamics mainly studies the source of the sudden violent change of nature and human society and its evolution. The impact of the system can be divided into endogenous and exogenous shocks. In this article, catastrophe theory is used to study the neuron system. Based on the mean field model of Hurst and Sornette, introducing the weight parameters, mathematical models are constructed to study the response characteristics of the neuron system in face of exogenous shocks, endogenous shocks, and integrated shocks. The time characteristics of the shock response of the neuron system are discussed too, such as the instantaneous and long-term response of the system in face of shocks, the different response forms according to the weight or linear superposition, and the influence of adjusting parameters on the neuron system. The research result shows that the authoritarian coefficient and weight coefficient have a very important influence on the response of neuron system; By adjusting the two coefficients, the purpose of disaster prevention, self-healing protection and response reducing can be well achieved.
- Neuron system shock superimposed response based on catastrophe dynamics


