Numerical simulation of continuous roll-casting process of aluminum alloy
XIE Shui-sheng(谢水生), YANG Hao-qiang(杨浩强), HUANG Guo-jie(黄国杰)
State Key Laboratory for Fabrication and Processing of Non-ferrous Metals,
Beijing General Research Institute for Non-ferrous Metals, Beijing 100088, China
Received 28 July 2006; accepted 15 September 2006
Abstract:
In order to improve the strip quality of continuous roll-casting process (CRP) of aluminum alloy, the investigations of the flow behavior within the metal pool, the heat transfer condition between roll and strip, the pouring temperature of molten alloy, the roll-casting speed and the control of the position of solidification final point are important. The finite volume method was applied to the analysis of the continuous roll-casting process. A two-dimensional incompressible non-Newtonian fluid flow with heat transfer was considered, which was described by the continuity equation, the Navier-Stokes equation and the energy equation. With this mathematical model, the flow patterns, temperature fields and solid fraction distributions in the metal pool between two rolls were simulated. From the calculated results, the effects of technical parameters to the position of solidification final point are obtained. The simulated results show that the roll-casting speed and pouring temperature have an enormous effect on the temperature distribution and the position of solidification final point.
Key words:
continuous roll-casting; numerical simulation; solid fraction; aluminum alloy;
1 Introduction
The technique of continuous roll-casting for fabrication of thin aluminum alloy strips provides a number of advantages over other fabrications methods, including remarkable energy savings and low cost[1-2]. However, the practical application of continuous roll-casting process was still hindered due to the crucial control of many casting conditions within the narrow variation ranges, such as pouring temperature of molten alloy, roll-casting speed and cooling intensity. It was found that the formability and surface quality of roll-casting strips were very sensitive to the variations of thermal distribution, flow condition and metal-roll interactions[3-9].
In order to improve the strip quality, it is important to investigate the flow behavior within the metal pool, the temperature field and the control of the position of solidification final point with the numerical simulation methods. HWANG et al[10] adopted the coupled set of governing differential equations for mass, momentum and energy balance with the finite element method to simulate the filling sequences, flow patterns and corresponding temperature profiles in the metal pool under an actual casting condition of a vertical twin-roll strip casting process. SANTOS et al[11] presented a numerical model for the two-dimensional solidification problem in the twin-roll continuous casting system by using a finite difference technique. JIN et al[12-13] developed a mathematical model to control the position of solidification final point by the two-dimensional heat and fluid-flow numerical calculation.
In this study, a two-dimensional incompressible non-Newtonian flow model with heat transfer was developed to simulate the continuous roll-casting process of aluminum alloy. The effects of the pouring temperature and roll-casting speed on the flow field, temperature field and solid fraction distribution were obtained. The main purpose was to investigate the effects of process parameters on the quality of roll-casting strip.
2 Mathematical modeling
2.1 Governing equations
The continuity equation is
![]() (1)
(1)
The Navier-Stokes equation is
![]() (2)
(2)
The energy equation is
![]() (3)
(3)
where ρ is the density; ui is the velocity of element i; xi is the displacement of element i; p is the pressure; δij is the Kronecker delta function; σij is the viscosity tension between element i and j; gi is the gravity acceleration of element i; c is the specific heat; T is the temperature; λ is the thermal conductivity coefficient; q(x) is the thermal source.
2.2 Viscosity model
The viscosity of molten alloy as the function of shearing rate changed drastically. Therefore, the dependency of viscosity on shearing rate must be established. In this paper, the non-Newtonian viscosity model in FLOW3D is Carreau model as follows[14]:
![]() (4)
(4)
where η0 is low shear rate viscosity (zero shear rate viscosity, g?s/cm); η∞ is the high shear rate viscosity (g?s/cm); λ is the time constant; ![]() is the shear rate; n is the power-law exponent of material. Here, this equation becomes Newtonian flow model if exponent n is 1.
is the shear rate; n is the power-law exponent of material. Here, this equation becomes Newtonian flow model if exponent n is 1.
2.3 Geometry and parameters
In the numerical simulation, the mesh of continuous roll-casting process is shown in Fig.1.
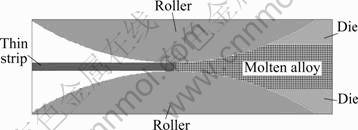
Fig.1 2D model and mesh of continuous roll-casting process
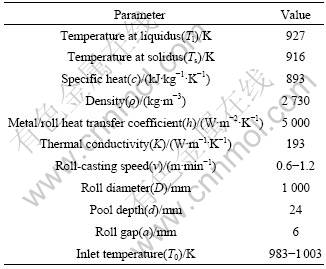
The material of roll-casting is 3003 aluminum alloy in this simulation, which the thermal physical properties and calculation conditions are presented in Table 1.
Table 1 Thermal physical properties and calculation conditions of 3003 aluminum alloy in continuous roll-casting process
3 Results and discussion
3.1 Change of temperature and solid fraction from beginning to steady state
In order to investigate how the metal pool could be progressively developed between two rolls and how the solidified layer could grow in thickness with time on the rotating roll surface, the computation of the change of the temperature and solid fraction from beginning to steady state. The casting conditions used for the case study are listed in following: pouring temperature T0= 993 K, roll-casting speed v=1.5 m/min. Fig.2 shows the changing of the temperature field and solid fraction at 0.0, 0.5, 1.0 and 1.5 s after cooling, respectively.
Fig.2(a) shows the distribution of the temperature and solid fraction at 0 s. It can be seen from Fig.2(a) that the temperature of molten alloy within the molten pool is 993 K and the solid fraction is 0. Fig.2(b) shows the distribution of the temperature and solid fraction at 0.5 s after cooling. The temperature of the molten alloy near to the roller drops down rapidly due to the high temperature difference between the molten alloy and the water-cooled rollers. The thickness of solidified layer grows to about 1 mm near the roll tip (or minimum roll gap). Fig.2(c) shows the distribution of the temperature and solid fraction at 1.0 s after cooling. The temperature near the roller surface is about 832 K, and the thickness of solidified layer increases to about 2 mm at the roll tip. However, the solidified layers are not bonded to each other since the roll gap is 6 mm and the solidified layer thickness grows to 3 mm at the roll tip for the two solidified layers to contact and press together. The temperature and solid fraction distribution at 1.5 s after cooling is shown in Fig.2(d). At this moment, the thickness of solidified layer grows to more than 3 mm at the roll tip where two solidified layers contact together. From the solid fraction distribution, the solidified layers weld to each other about 7 mm at the right of the roll tip which is the position of solidification final point. Therefore, the solidification in the roll gap is completed and ready for the following operation. At this moment, the solidified strip is withdrawn from the roll tip and has been rolled. According to the numerical results, the roll-casting speed must be controlled strictly and the contact time between the roller and strip exceeds 1.5 s under these conditions. That is to say, only when the roll-casting speed is lower than the definite value, the roll-casting strip can be solidified at roll gap, and CRP can be finished successfully.

Fig.2 Distribution of temperature (A) and solid fraction (B) at different time after cooling: (a) t=0 s; (b) t=0.5 s; (c) t=1.0 s; (d) t=1.5 s
3.2 Effect of roll-casting speed on position of solidifica- tion final point
In order to study the effect of the roll-casting speed v on the position of solidification final point, the various roll-casting speed ranges from 0.6 to 1.2 m/min were investigated. At the same time, the inlet temperature of semi-solid slurry is 993 K. Fig.3 shows the distributions of temperature and solid fraction with roll-casting speed of 0.6, 0.8, 1.0 and 1.2 m/min, respectively. The results show that different roll-casting speed has an enormous effect on the temperature field and the position of solidification final point. That is to say, the distance from the solidification final point to roll tip increases with the decrease of the roll-casting speed. The distances are about 36, 33, 30 and 24 mm for condition Figs.3(a)-(d), respectively. The calculated results are consistent with the experimental ones.

Fig.3 Distribution of temperature (A) and solid fraction (B) for different roll-casting speeds: (a) v=0.6 m/min; (b) v=0.8 m/min; (c) v=1.0 m/min; (d) v=1.2 m/min
3.3 Effect of pouring temperature of molten alloy on temperature distribution
Fig. 4 shows the distribution of temperature and solid fraction when pouring temperatures are 973, 983, 993 and 1 003 K, respectively. From Fig.4, the pouring tempera- ture has an enormous effect on the distribution of temperature and solid fraction. That is to say, the distance from the solidification final point to roll tip increases with the decrease of the pouring temperature.

Fig.4 Distribution of temperature (A) and solid fraction (B) at different pouring temperatures: (a) T0=973 K; (b) T0=983 K; (c) T0=993 K; (d) T0=1 003 K
3.3 Effect of cooling intensity of roller on solidification final point
The effect of cooling intensity of the roller to the solidification final point is equivalent to the effect of the roll-casting speed in the theory, so the simulated results of the cooling intensity of the roller may refer the simulated results of the roll-casting speed above.
4 Conclusions
1) The distribution of temperature and solid fraction during the initial solidified stage is obtained, and this helps to understand the procedure of developing a metal pool and the formation of a solidified shell. Only when the roll-casting speed is lower than a definite value under specified cooling condition, the roll-casting strip can be solidification at roll gap, and CRP can be finished successfully.
2) Both the roll-casting speed and pouring temperature have an enormous effect on the temperature distribution and the position of solidification final point. The calculated results are consistent with the experimental ones.
3) Improving the cooling intensities of the rollers can enhance roll-casting speed and productivity.
References
[1] TOSHIO H, SHINSUKE S. Study on high-speed twin-roll caster for aluminum alloys [J]. Journal of Materials Processing Technology, 2003, 143/144: 895-900.
[2] HAGO T, TKAHASHI K, IKAWAAND M, WATARI H. Twin roll casting of aluminum alloy strips [J]. Journal of Materials Processing Technology, 2004, 153/154: 42-47.
[3] KANG C G, KIM Y D, LEE S W. A coupled solidification analysis of materials and cooling roller in direct rolling process [J]. Journal of Materials Processing Technology, 1997, 66: 277-286.
[4] KIM W S, KIM D S, KUZNETSOV A V. Simulation of coupled turbulent flow and heat transfer in the wedge-shaped pool of a twin-roll strip casting process [J]. International Journal of Heat and Mass Transfer, 2000, 43: 3811-3822.
[5] TAN Li-jian, SHEN Hou-fa, LIU Bai-cheng. Numerical simulation on heat transfer and fluid flow in continuous casting [A]. The First Sino-Korean Conference on Advanced Manufacturing Technology [C]. Beijing, 2001: 32-41.
[6] PARK C M, KIM W S, PARK G J. Thermal analysis of the roll in the strip casting process [J]. Mechanics Research Communications, 2003, 30: 297-310.
[7] CHANG J G, CHENG I W. Analysis of flow and heat transfer in twin-roll strip casting process [J]. International Journal of Heat and Mass Transfer, 1998, 41(2): 475-487.
[8] GUTHRIE R I L, TAVARES R P. Mathematical and physical modeling of steel flow and solidification in twin-roll/horizontal belt thin-strip casting machines [J]. Applied Mathematical Modeling, 1998, 22: 851-872.
[9] DU Yan-ping, YANF Jian-wei, LIANG Ai-sheng, SUN Bin-yu. 3D numerical simulation for flowing field coupled with temperature field in strip rolling casting mould [J]. Special Casting and Nonferrous Alloys, 2004(1): 41-43. (in Chinese).
[10] HWANG J D, LIN H J, HWANG W S, HU C T. Numerical simulation of metal flow and thermal transfer during twin roll strip casting [J]. ISIJ International, 1995, 35(2): 170-177.
[11] SANTOS C A, SPIM J A, GARCIA A. Modeling of solidification in twin-roll strip casting [J]. Journal of Materials Processing Technology, 2000, 102: 33-39.
[12] JIN Zhu-mei, HAO Ji-cheng. Numerical model of solidifaction end in twin-roll casting process [J]. The Chinese Journal of Nonferrous Metals, 1998, 8(2): 694-695. (in Chinese)
[13] JIN Zhu-mei, HAO Ji-cheng, XU Guang-juan. Numerical simulation of flow, temperature and thermal stress fields during twin-roll casting process [J]. Acta Metallurgica Sinica, 2000, 36(4): 391-394. (in Chinese)
[14] Flow-3d Users Manual. Flow Science [M]. USA: 2002.
Foundation item: Projects(50374014; 50674017) supported by the National Natural Science Foundation of China
Corresponding author: XIE Shui-sheng; Tel: +86-10-82241265-221; E-mail: xiess@grinm.com



