Trans. Nonferrous Met. Soc. China 30(2020) 3356-3366
New correction method for controlled-source electromagnetics source effects
Bo YUAN1,2,3, Di-quan LI 1,2,3, Yan-fang HU1,2,3
1. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring of Ministry of Education (Central South University), Changsha 410083, China;
2. Hunan Key Laboratory of Non-ferrous and Geological Hazard Detection, Changsha 410083, China;
3. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China
Received 2 March 2020; accepted 19 August 2020
Abstract:
A novel method for source effect correction based on integral equation method is proposed. By taking the electrical horizontal field Ex of current source as an example, the correction method is validated using both simulated data and field data. The results show that the correction method is feasible and effective for isotropic media. When the field data are processed, the correction method normalizes the sources with different geological structures, which eliminates the geological difference among sources, and retains the geological difference among receivers. The correction results are in line with the expectation in whole.
Key words:
source effect; controlled-source electromagnetics; source overprint effect; shadow effect;
1 Introduction
Controlled-source electromagnetic (CSEM) data are often influenced by source effects, including non-plane-wave effects, source overprint effects and shadow effects. In the actual exploration, the geologic structure beneath the sources is usually unknown, so the source effects are inevitable, making field data processing and geological inference difficult.
The non-plane-wave effects are caused by the serious distortion of the Cagniard apparent resistivity in the near-field zone. Using the full region apparent resistivity rather than the Cagniard apparent resistivity can avoid this problem [1-3]. But, this method cannot solve the source overprint and shadow effects.
The source overprint effects are caused by the geologic structure beneath the source [4]. They mainly affect the electric and magnetic fields, and not the Cagniard apparent resistivity in the far-field zone [5]. The source overprint effects are difficult to eliminate, so they should be avoided in practice [5]. SUN et al [6] thought that the source overprint effects are similar to the static effect under certain conditions. Such source overprint effects are called the source static displacement, which can be suppressed by the normal static displacement correction method. But this method only works for the shallow anomaly. LIN et al [7] believed that the 3D terrain near the source also affects the frequency response curves of the receivers, which is also a kind of source overprint effects [8,9].
The shadow effects are caused by the geologic structure between the source and the receivers [10]. YAN and FU [11] reported that the shadow effects are caused by the formation wave under three conditions. After analyzing the characteristics and influence factors of the shadow effects, SUN et al [6] designed a method to filter out the shadow effects by suppressing the formation wave. This method, however, is affected by human factors, because different suppression coefficients lead to different correction accuracies.
With the deepening of prospecting targets, CSEM is more important in mineral exploration [12]. Because ore deposits are often formed in the active tectonic belts [13-15], source overprint and shadow effects influence the CSEM data seriously, leading to the incorrect geoelectric structure and burial depth. The Cagniard apparent resistivity is less affected in the far-field zone, but part of information is lost in deep exploration. So, it is of great significance to eliminate the influence of the source overprint and shadow effects on the magnetic and electric field data.
Those earlier studies did not make clear distinction between source overprint and shadow effects. The source overprint effects were considered as a kind of shadow effect [11], or vice versa [5]. And most of those studies were focused on the properties and characteristics of source overprint effects [16-18], rather than the methods of processing or corrections. Researches on the way to eliminate the source overprint and shadow effects are necessary [19]. Therefore, in this study, a novel method is proposed for eliminating the source effects based on the integral equation (IE) algorithm.
2 Integral equation method
The IE method is often used for the numerical simulation of electromagnetic fields. Since the IE method only needs to discrete the anomaly and is simple to calculation [20,21], it may work for source effects correction. It is proposed to use the IE method for source effects calculation and correction, and verify it using a three-dimensional (3D) model of a homogenous half-space with a single conductive anomaly.
As shown in Fig. 1, in the 100 Ω·m homogeneous half-space, there is a 10 Ω·m anomaly with the side length of 300 m and the top buried depth of 300 m. The source length is 1 km, the current is 10 A, and the frequency is 32 Hz. The grid is 30 m × 30 m × 30 m, and the grid numbers are 10 × 10 × 10. The scattering electric field Exa and scattering magnetic field Hya are calculated along the section passing through the center of the anomaly. The calculated results are compared with those of INTEM3DQL [22] in Fig. 2, which was developed by the Consortium for Electromagnetic Model and Inversion (CEMI) at the University of Utah. Basically, these two results are consistent. The relative difference of Exa is less than 1%, as well as Hya, except that the part inside the frame is slightly higher. The results indicate that the 3D forward electromagnetic field results are reliable. The 3D forward modeling program can be used as the basis of the source effect correction program.
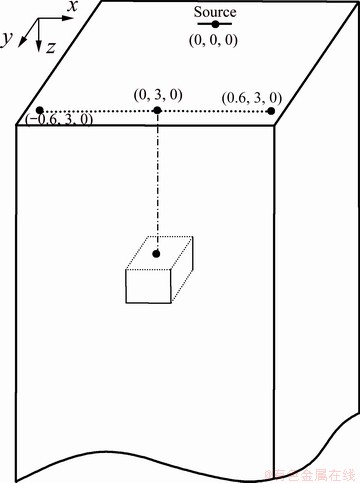
Fig. 1 Three-dimensional (3D) model of homogenous half-space with single conductive anomaly (unit: km)
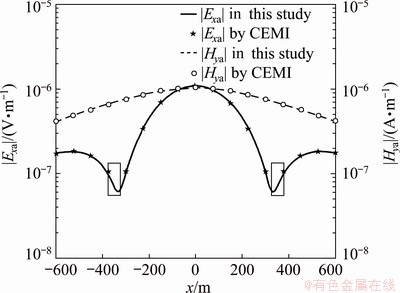
Fig. 2 Scattering electric field Exa and magnetic field Hya of single conductive anomaly (f=32 Hz) obtained by this study and CEMI [22]
3 Numerical simulation
Among the components of electromagnetic field, Ex is mostly affected by source overprint and shadow effects [6]. Therefore, we choose Ex for the numerical simulation of source effects and the correction research.
We establish two models (Model I and Model II) with a single anomaly in a three-layer media. Figure 3 shows the sketch of Model I. From top to bottom, the resistivity of each layer is 100, 1000 and 100 Ω·m, and the thickness is 0.5 km, 2 km and infinite, respectively. The source center is taken as the coordinate origin. The x and y directions are parallel and perpendicular to the source, respectively. The receivers are located at (4.5 km, 10 km, 0 km). Beneath the source, there is an anomaly with a size of 2 km × 2 km × 0.3 km, with the center located at (0 km, 0 km, 0.35 km) and the resistivity the same as that of the middle layer. Model II is similar to Model I, but the resistivity of the middle layer and the anomaly is 10 Ω·m.
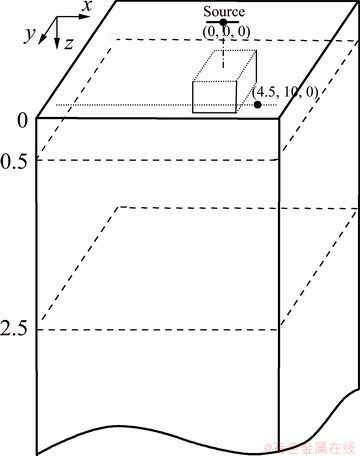
Fig. 3 Sketch of Model I (Unit: km)
As Fig. 4 shows, there is a log-log relationship between frequency and electric field amplitude of the receivers. Both the conductive and resistive anomalies beneath the source affect the electric field of the receivers. The anomaly beneath the source does not affect the high-frequency data of the electric field because of the insufficient skin depth. But the low-frequency data of the electric field are affected and show curve translation, which is similar to the static effect.
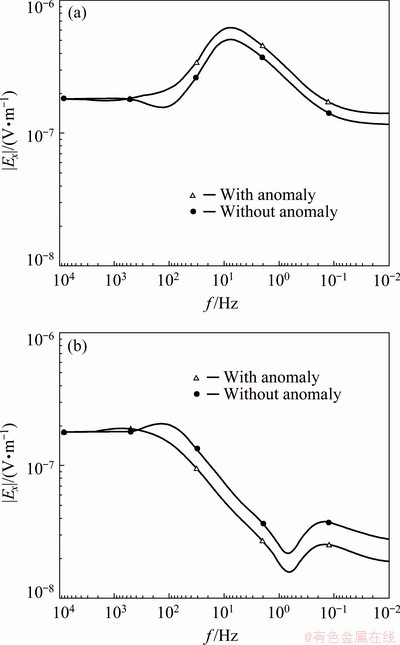
Fig. 4 Ex amplitude curve of receiver in Model I (a) and Model II (b)
If we exchange the position of the source and receiver in Model I and Model II, the location of the anomaly will move from being beneath the source to being beneath the receiver. We calculate the scattering electric field Exa (Fig. 5). The real part and imaginary part of Exa do not change, indicating that the measured data contain the geological information beneath both the receiver and the source. In practice, only the information beneath the receiver is needed, so the information beneath the source is regarded as the interference.
The results in this section show that the source effects are common, no matter in the far or near field. Specifically, the source overprint effects influence the distribution of electromagnetic field energy, and they widely exist in the data of the whole region. The shadow effects influence the energy dissipation in the electromagnetic field propagation, and they exist in the data of non-far regions.
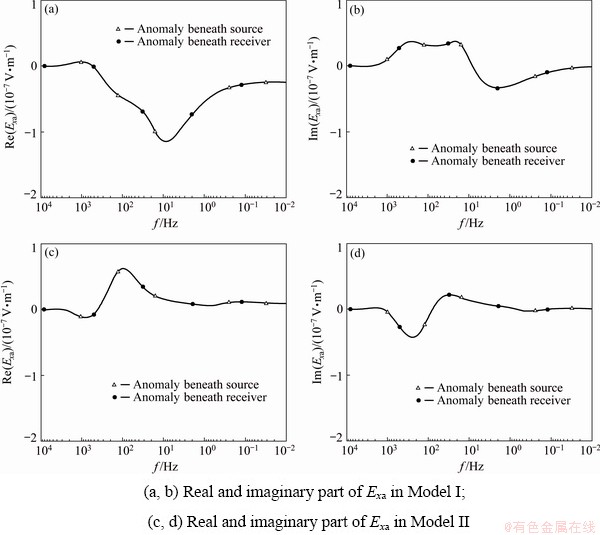
Fig. 5 Exa before and after exchanging positions of source and receiver
4 Source effect correction method
In exploration, a long survey line needs multiple sources, and the sources are often located at different geologic conditions. The sources of the main line and the connecting line are also located in different geologic structures in general. Therefore, the filed measurements and the inversion results are often inconsistent at the intersection of different sources. In such case, the processing and interpretation of the data are difficult, but extra information can be obtained at the intersection. If the geologic structure is assumed to be isotropic beneath these receivers, the source effects can be corrected using the data at the intersection of different sources.
On the basis of the IE method, we propose a source effect correction method and demonstrate it by a long survey line with multiple sources (Fig. 6). The proposed method has the following four steps.
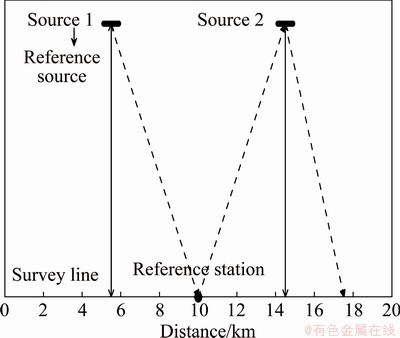
Fig. 6 Long survey line with multiple sources
(1) Establishing background model of survey area
Select Source 1 as the reference source and station No. 100 which is 10 km from the left end of the survey line as the reference station. Perform one-dimensional (1D) inversion for the data of the reference station with Source 1. The inversion result is used to establish the background model.
(2) Calculating scattering field of reference station
Calculate the background field Eb(r) at the reference station with Source 2 in the established background model. The difference between Eb(r) and the measured E(r) at the reference station with Source 2 is considered as the scattering field (Ea(r)) caused by the geologic difference beneath Source 2 and Source 1. According to the Born approximation, the total field at the reference station can be expressed as
E(r)= Eb(r)+Ea(r)=Eb(r)+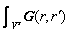
△σ(r')·Eb(r')dV (1)
(3) Assuming equivalent anomaly and calculating its scattering current
The scattering current source is assumed to be a simple 3D body located directly beneath Source 2 with certain size, buried depth and occurrence to calculate the dyadic Green’s function G(r,r'). Assuming that the conductivity inside the 3D body is consistent, we have
E(r)=Eb(r)+△σaql(r')·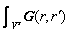Eb(r')dV (2)
Thus, we can get the △σaql(r') by
△σaql(r')=(E(r)-Eb(r))/(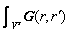Eb(r')dV) (3)
(4) Calculating scattering field of other stations
Similarly, according to the Born approximation, the influence of the equivalent anomaly on other receivers (Ea(r'')) can be calculated by
Ea(r'')=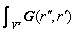
△σaql(r')·Eb(r'')dV (4)
Regarding the field data of other receivers with Source 2 as E(r''), we have
Eb(r'')=E(r'')-Ea(r'') (5)
where Eb(r'') is the source effect correction result.
This source effect correction method is based on the equivalent field in electromagnetics. Only considering the influence of the geologic difference and replacing it with an equivalent anomaly, this method doesn’t need to calculate the parameters of the geologic difference beneath different sources. This method can effectively and accurately correct the source effects, which is conducive to understand the geoelectric structure beneath the receivers.
5 Validation of source effect correction method
5.1 Anomaly beneath source and correction station
We establish Model III with two sources to test whether the source effect correction is effective when the anomaly are beneath the source and the correction station (Fig. 7). The background is a three-layer model. From top to bottom, the resistivity of each layer is 100, 1000 and 100 Ω·m, and the thickness is 0.5 km, 2 km and infinite, respectively. The midpoint of the centers of the two sources is taken as the coordinate origin. The x and y directions are parallel and perpendicular to the source, respectively. The survey line is from (-10 km, 10 km, 0 km) to (10 km, 10 km, 0 km). The section between (-10 km, 10 km, 0 km) and (1 km, 10 km, 0 km) is measured when Source 1 is used, and the one from (-1 km, 10 km, 0 km) to (10 km, 10 km, 0 km) is measured when Source 2 is used. There are two 2 km × 2 km × 1 km anomaly in this model. One is beneath the survey line (referred to as anomaly No. 1) and the other is beneath Source 2 (referred to as anomaly No. 2). The centers of anomaly No.1 and No.2 are at (7.5 km, 10 km, 0.75 km) and (4.5 km, 0 km, 0.75 km), respectively.
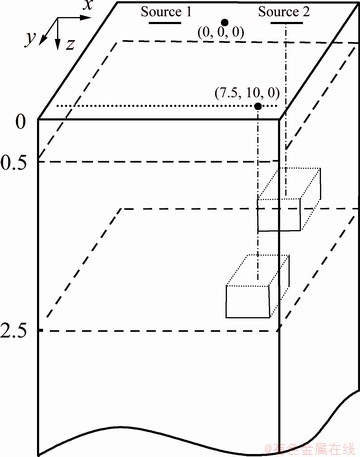
Fig. 7 Sketch of Model III with anomaly beneath source and correction station (Unit: km)
The Ex data at station (7.5 km, 10 km, 0 km) are corrected using Source 1 as the reference source and station (0 km, 10 km, 0 km) as the reference station (Fig. 8). Figure 8(a) shows the Ex data before (Ex_be) and after (Ex_af) correction, as well as the standard data (Ex_st). The standard data are defined as the Ex data of the correction station without anomaly No. 2 beneath Source 2. The percentage difference (D) is shown in Fig. 8(b), which is calculated by the following formula:
Dbe=|(|Ex_be|-|Ex_st|)/|Ex_st||×100% (6)
Daf =|(|Ex_af|-|Ex_st|)/|Ex_st||×100% (7)
where Dbe represents the intensity of source effects, and Daf is also the correction error.
After the correction, the average and the maximum correction errors of Ex amplitude are 0.37% and 0.76%, respectively.
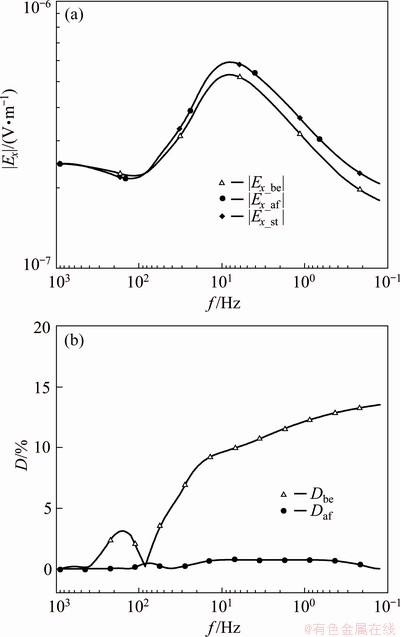
Fig. 8 |Ex_be|, |Ex_af| and |Ex_st| of correction station (a) and Dbe and Daf of correction station (b) for case with anomaly beneath source and correction station
5.2 Anomaly beneath source and reference station
We establish Model IV to validate the source effect correction method for the case with anomaly beneath the source and the reference station. Model IV is similar to Model III, but the center of anomaly No. 1 is moved to (0 km, 10 km, 0.75 km) beneath the reference station. The projection of the anomaly center on the surface overlaps the reference station. So, in source effects correction, the background model established by the 1D inversion of the reference station is different from that of Model IV.
We correct the source effects of two stations to analyze the influence of different reference sources. One station (7.5 km, 10 km, 0 km) is corrected using Source 1 as the reference source and station (0 km, 10 km, 0 km) as the reference station. In this case, the anomaly is beneath the correction source and reference station. The other station (-7.5 km, 10 km, 0 km) is corrected using Source 2 as the reference source and station (0 km, 10 km, 0 km) as the reference station. In this case, the anomaly is beneath the reference source and reference station.
For the case with anomaly beneath the correction source and the reference station, the standard data are defined as the Ex data of the correction station without anomaly No. 2 beneath Source 2. When establishing the background model of the survey area for source effect correction, the average fitting error of the reference station is 0.33%, and the maximum fitting error is 0.93%, which is near 16 Hz. After correction, the average and the maximum D values of the Ex amplitude are 0.88% and 1.75%, respectively. It can be seen from Fig. 9 that the correction results are generally good, but the correction errors are positively correlated with the inversion fitting error near 16 Hz, indicating that the correction errors near 16 Hz are caused by the 1D inversion of the reference station.
The results in Fig. 9 show that when there is an anomaly beneath the reference station, the background model obtained by 1D inversion may be significantly different from the actual background model, but it can still be used as the reference background.
For the case with anomaly beneath the reference source and reference station for source effect correction, the standard data are defined as the Ex data of the correction station when an anomaly of 2 km × 2 km × 1 km exists beneath Source 1. When establishing the background model of the survey area, the average fitting error of the reference station is 1.18%, and the maximum fitting error is 3.51%, which is near 16 Hz. After the correction, the average and maximum D values of Ex amplitude are 0.72% and 2.06%, respectively. As Fig. 10 shows, the correction results are generally good, but there are correction errors positively correlated with the inversion fitting error near 16 Hz, indicating that the correction errors near 16 Hz are caused by the 1D inversion of the reference station.
The results in Fig. 10 show that after the source effect correction, the data of the correction station are equivalent to the case with a 2 km × 2 km × 1 km anomaly beneath Source 1, which is the same as the geologic structure beneath Source 2. This means that the geologic structure beneath the field source is normalized, which is very significant in the field exploration. Due to the complex or unknown geologic conditions beneath the field source, it is difficult to select an appropriate field source location. Normalizing the sources can ensure the consistency of the whole survey line processing and interpretation.
5.3 Changing anomaly center
We establish Model V to test whether the source effect correction is effective when the position of anomaly center changes. Model V is similar to Model III, but the size and the center of the anomaly No. 2 are 3 km × 3 km × 1 km and (5 km, 0.5 km, 0.75 km), respectively.
The standard data are defined as the Ex data of the correction station without anomaly No. 2 beneath Source 2. As shown in Fig. 11, after the correction, the average and the maximum Daf of Ex amplitude are 0.83% and 3.68%, respectively. High correction errors appear at the frequencies beneath 0.5 Hz, which are in the near field zone. The results show that the correction method is feasible, though the position of the anomaly beneath the source is uncertain.
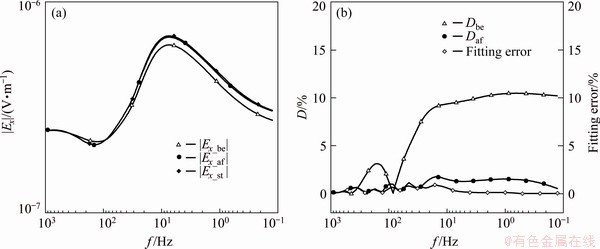
Fig. 9 |Ex_be|, |Ex_af| and |Ex_st| of correction station (a), and Dbe and Daf of correction station and fitting error of reference station (b) for case with anomaly beneath correction source and reference station
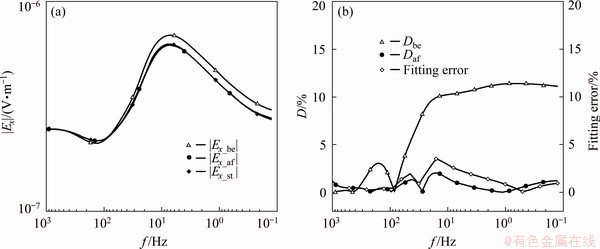
Fig. 10 |Ex_be|, |Ex_af| and |Ex_st| of correction station (a), and Dbe and Daf of correction station and fitting error of reference station (b) for case with anomaly beneath reference source and reference station
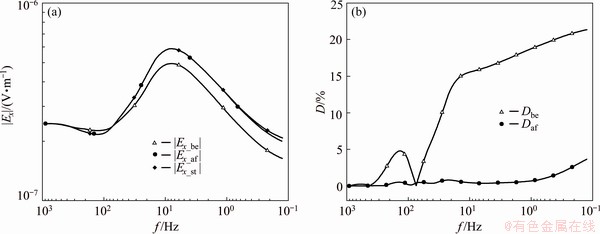
Fig. 11 |Ex_be|, |Ex_af| and |Ex_st| (a), and Dbe and Daf (b) of correction station with anomaly center changed
6 Field data processing
We apply the proposed method to the field data. In the study area HM, four CSEM sections are arranged with a total length of 385 km and station distance of 100 m (Fig. 12). The shortest and the longest survey lines are 86 and 112 km, respectively. 21 sources are used for the four survey lines. We measure the Ex component and calculate the full region apparent resistivity. Due to the source effects, the field measurement and inversion results are often inconsistent at the intersections of different sources. Therefore, combining the high quality CSEM data with effective geological information of several survey line sections is important. The proposed correction method is applied to two survey line sections to verify the effectiveness in the field data processing. One section is with sources A6B6 and A7B7, and the other is with sources A1B1 and A2B2.
Firstly, a 2.4 km section from receiver No. 1049-1072 of the survey line HM2 is measured using the source A6B6 and source A7B7, separately. The positions of the sources and the receivers are shown in Fig. 12.
Figure 13 shows the apparent resistivity curves of the receivers when different sources are used. The apparent resistivity of the whole survey line is high when source A7B7 is used, and that of the low-frequency section is higher than that of the high-frequency section. The apparent resistivity varies with different frequencies, but that at the same frequency of different stations is obviously similar.
Fig. 12 Measurement system and test stations of source effects in HM study area
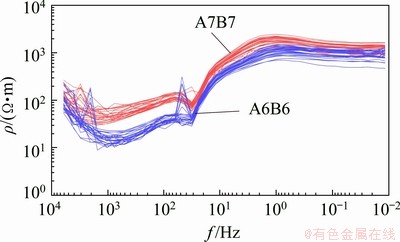
Fig. 13 Apparent resistivity of receivers with different sources used
According to the fitting error of the 1D inversion, station No. 1052 (fitting error of 14%) and source A6B6 are selected as the reference station and the reference source, respectively, to correct the data of each station with source A7B7 (Fig. 14). Although the receivers have different observation angles when different sources are used, the apparent resistivity curves with source A6B6 still can be used as references (black line in Fig. 14) to test the correction accuracy. The result shows that the correction accuracy is in line with the expectation.
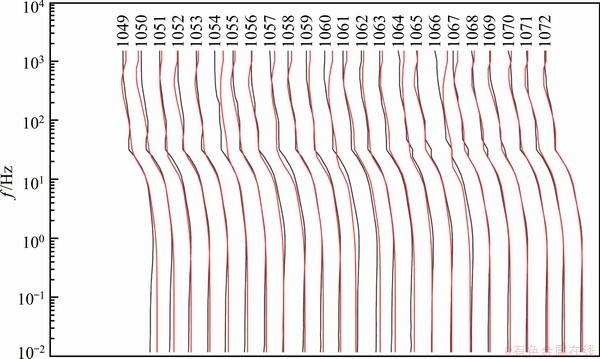
Fig. 14 Apparent resistivity of receivers with source A7B7 after source effect correction (red) and reference curves (black)
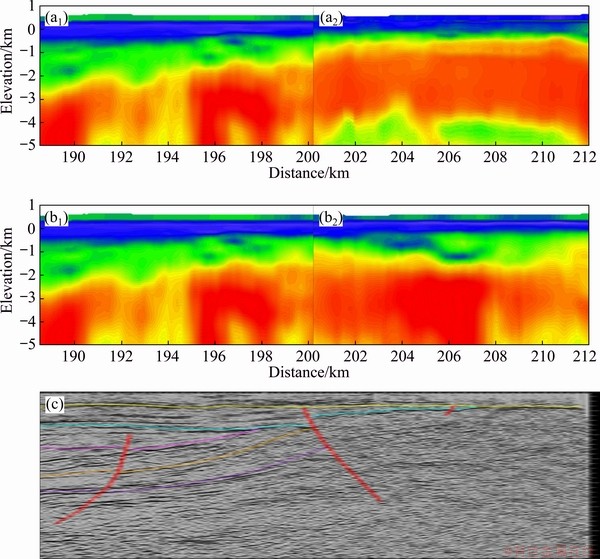
Fig. 15 Inversion before (a) and after (b) correction with source A1B1 (a1, b1) and source A2B2 (a2, b2) and seismic profile (c)
Secondly, a section of survey line HM4 is selected for source effect correction (solid lines in Fig. 12), and the corrected results are compared with the seismic results. The inversions of station 2002 with source A1B1 and source A2B2 are different. The basement of the receivers with source A2B2 is deeper than that with source A1B1 (Fig. 15(a)). Then, we correct the data of each station with source A1B1, using source A2B2 as the reference source and station 2002 as the reference station. As Fig. 15(b) shows, the source effect has been significantly mitigated, and the corrected data are in good agreement with the seismic results (Fig. 15(c)).
7 Conclusions
(1) The source overprint effects influence the distribution of electromagnetic field energy, and widely exist in the data of the whole region. The shadow effects influence the energy dissipation in electromagnetic field propagation, and exist in the data of non-far region.
(2) The validation experiments show that the proposed correction method can reduce the source effects and keep the differences of receivers at the same time. The correction result is in line with the expectation in whole. This method is feasible and effective for isotropic media. Essentially, the correction method is the normalization of the geologic structure beneath the source.
(3) It is difficult to simulate the geologic difference beneath the sources by an equivalent anomaly in the near field data. The change of receiver station leads to great changes in the equivalent anomaly parameters that are calculated based on different receivers. So, the correction method works better for the source overprint effects than the shadow effects.
References
[1] HE J S. Wide field electromagnetic methods [C]//SEG Technical Program Expanded Abstracts 2015. Tulsa: Society of Exploration Geophysicists, 2015: 1006-1011.
[2] XUE Guo-qiang, CHEN Wei-ying, ZHOU Nan-nan, LI Hai. Short offset TEM technique with a grounded wire source for deep sounding [J]. Chinese Journal of Geophysics, 2013, 56(1): 255-261. (in Chinese)
[3] LUAN Xiao-dong, DI Qing-yun, LEI Da. Near-field correction of CSAMT data based on Newton iteration method and GA method [J]. Chinese Journal of Geophysics, 2018, 61(10): 4148-4159. (in Chinese)
[4] MACINNES S C. Lateral effects in controlled source audiomagnetotellurics [D]. Tucson: Tucson University of Arizona, 1988.
[5] TANG Jing-tian, HE Ji-shan. Controllable source audio magnetotelluric method and its application [M]. Changsha: Central South University Press, 2005. (in Chinese)
[6] SUN Ya, HE Zhan-xiang, LIU Jian-xin, LIU Ying, TONG Xiao-zhong. Simulation study for long wire source frequency-domain electromagnetic sounding field source static displacement [J]. Oil Geophysical Prospecting, 2011, 46(1): 149-154. (in Chinese)
[7] LIN C, ZHONG S, AUKEN E, CAI H, PENG M, KONG W. The effects of 3D topography on controlled-source audio- frequency magnetotelluric responses [J]. Geophysics, 2018, 83(2): WB97-WB108.
[8] XUE Guo-qiang, YAN Shu, CHEN Wei-ying. A fast topographic correction method for electromagnetic data [J]. Chinese Journal of Geophysics, 2016, 59(12): 4408-4413. (in Chinese)
[9] LI Jing-he, HE Zhan-xiang, MENG Shu-jun, YANG Jun, LI Wen-jie, LIAO Xiao-qian. Domain decomposition based integral equation modeling of 3-dimensional topography in frequency domain for well electromagnetic field [J]. Acta Physica Sinica, 2019, 68(14): 140202. (in Chinese)
[10] KUZNETZOV A N. Distorting effects during electro- magnetic sounding of horizontally non-uniform media using an artificial field source [J]. Earth Physics, 1982, 18(1): 130-137.
[11] YAN S, FU J M. An analytical method to estimate shadow and source overprint effects in CSAMT sounding [J]. Geophysics, 2004, 69(1): 161-163.
[12] HU Y F, LI D Q, YUAN B, SUO G Y, LIU Z J. Application of pseudo-random frequency domain electromagnetic method in mining areas with strong interferences [J]. Transactions of Nonferrous Metals Society of China, 2020, 30(3): 774-788.
[13] MAO X C, ZHAO Y, DENG H, ZHANG B, LIU Z K, CHEN J, ZOU Y H, LAI J Q. Quantitative analysis of intrusive body morphology and its relationship with skarn mineralization—A case study of Fenghuangshan copper deposit, Tongling, Anhui, China [J]. Transactions of Nonferrous Metals Society of China, 2018, 28(1): 151-162.
[14] ZOU Y H, LIU Y, PAN Y, YANG K D, DAI T G, MAO X C, LAI J Q, TIAN H L. Numerical simulation of hydrothermal mineralization associated with simplified chemical reactions in Kaerqueka polymetallic deposit, Qinghai, China [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(1): 171-183.
[15] WANG F Y, MAO X C, DENG H, ZHANG B Y Manganese potential mapping in western Guangxi-southeastern Yunnan (China) via spatial analysis and modal-adaptive prospectivity modeling [J]. Transactions of Nonferrous Metals Society of China, 2020, 30(4): 1058-1070.
[16] LEI D, WU X P, DI Q Y, WANG G, LV X R, WANG R, YANG J, YUE M X. Modeling and analysis of CSAMT field source effect and its characteristics [J]. Journal of Geophysics and Engineering, 2016, 13(1): 49-58.
[17] ZHOU N N, HOU D Y, XUE G Q. Effects of shadow and source overprint on grounded-wire transient electromagnetic response [J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(8): 1169-1173.
[18] WANG X X, DENG J Z. Distortion effects caused by the target abnormal bodies in CSAMT exploration [C]//International Workshop on Gravity, Electrical & Magnetic Methods and Their Applications. Xi’an: Chinese Geophysical Society, Society of Exploration Geophysicists, 2019: 101-104.
[19] HE Zhan-xiang. Opportunities, challenges and development directions of electromagnetic exploration today [J]. Computing Techniques for Geophysical and Geochemical Exploration, 2019, 41(4): 433-447. (in Chinese)
[20] CHEN Gui-bo, WANG Hong-nian, YAO Jing-jin, HAN Zi-ye. Three-dimensional numerical modeling of marine controlled-source electromagnetic responses in a layered anisotropic seabed using integral equation method [J]. Acta Physica Sinica, 2009, 58(6): 3848-3857. (in Chinese)
[21] LI Di-quan, XIE Wei, CHENG Dang-xing. Three- dimensional modeling for E-Ex wide field electromagnetic methods [J]. Chinese Journal of Nonferrous Metals, 2013, 23(9): 2459-2470. (in Chinese)
[22] WANG Ruo, DI Qing-yun, WANG Miao-yue, WANG Guang-jie. Research on the effect of 3D body between transmitter and receivers on CSAMT response using Integral Equation method [J]. Chinese Journal of Geophysics, 2009, 52(6): 1573-1582. (in Chinese).
人工源电磁法中场源效应校正方法
袁 博1,2,3，李帝铨1,2,3，胡艳芳1,2,3
1. 有色金属成矿预测与地质环境监测教育部重点实验室(中南大学)，长沙 410083；
2. 有色资源与地质灾害探测湖南省重点实验室，长沙 410083；
3. 中南大学 地球科学与信息物理学院，长沙 410083
摘 要：提出一种基于积分方程法的场源效应校正方法，以电偶源的水平电场分量Ex为研究对象，通过数值模拟验证该校正方法的有效性，并将其应用于实际资料处理中。结果表明，对于各向同性介质，基于积分方程法，采用等效异常体对场源效应进行校正的方法是可行和有效的。处理实际数据时，该校正方法将位于不同地质构造上的场源归一化，在保留各测点数据差异性的同时消除场源导致的差异，校正结果整体符合预期。
关键词：场源效应；人工源电磁法；场源复印效应；阴影效应
(Edited by Bing YANG)
Foundation item: Project (2018YFC0807802) supported by the National Key R&D Program of China; Project (41874081) supported by the National Natural Science Foundation of China
Corresponding author: Di-quan LI; Tel: +86-15802637512; E-mail: lidiquan@csu.edu.cn
DOI: 10.1016/S1003-6326(20)65467-X
Abstract: A novel method for source effect correction based on integral equation method is proposed. By taking the electrical horizontal field Ex of current source as an example, the correction method is validated using both simulated data and field data. The results show that the correction method is feasible and effective for isotropic media. When the field data are processed, the correction method normalizes the sources with different geological structures, which eliminates the geological difference among sources, and retains the geological difference among receivers. The correction results are in line with the expectation in whole.
