Trans. Nonferrous Met. Soc. China 24(2014) 3486-3491
Constitutive equations for high temperature flow stress prediction of 6063 Al alloy considering compensation of strain
Chun-lei GAN1, Kai-hong ZHENG1, Wen-jun QI1, Meng-jun WANG2
1. Guangzhou Research Institute of Non-ferrous Metals, Guangzhou 510650, China;
2. Key Laboratory of Nonferrous Metal Materials Science and Engineering of Ministry of Education, Central South University, Changsha 410083, China
Received 8 January 2014; accepted 5 March 2014
Abstract:
In order to develop the appropriate constitutive equation which can precisely model high temperature flow stress of 6063 Al alloy, a series of isothermal hot compression tests were performed at temperatures from 573 to 773 K and strain rates from 0.5 to 50 s-1 on a Gleeble-1500 thermo-simulation machine. Zener–Hollomon parameter in an exponent-type equation was used to describe the combined effects of temperature and strain rate on hot deformation behaviour of 6063 Al alloy, whereas the influence of strain was incorporated in the developed constitutive equation by considering material constants (a, n, Q and A) to be 4th order polynomial functions of strain. The results show that the developed constitutive equation can accurately predict high temperature flow stress of 6063 Al alloy, which demonstrates that it can be suitable for simulating hot deformation processes such as extrusion and forging, and for properly designing the deformation parameters in engineering practice.
Key words:
6063 Al alloy; constitutive equation; flow stress; strain; hot deformation;
1 Introduction
6063 Al alloy is one of the representative aluminium alloys. This alloy has an attractive combination of characteristics such as high specific strength, high corrosion resistance and easy workability, which make it an ideal choice for structural applications. It is well known that plastic deformation conditions, such as temperature, have an important influence on the deformation behavior of 6063 Al alloy [1,2]. Therefore, it is of vital importance to thoroughly study the high temperature deformation behavior of 6063 Al alloy for the purpose of the deformation parameter optimization.
Constitutive equation which describes the flow behavior of materials has been widely cited to stimulate the materials response under different plastic deformation conditions. It is an essential input for computer modeling thermomechanical process using finite element methods. The reliability of simulation results greatly depends on the accuracy of prediction of the constitutive equation. Therefore, great efforts have been made to propose various analytical, phenomenological and empirical equations which are essential to predict the flow stress in a wide range of materials [3-8]. Although these constitutive equations are relatively successful in prediction, more efforts are still needed to further enhance the accuracy of prediction. Recently, in the phenomenological approach which was proposed by SELLARS and McTEGARTA [9], a sine hyperbolic constitutive equation was revised by incorporation of strain dependent term to predict high temperature flow behaviour of alloys [10-14]. The revised sine hyperbolic constitutive equation exhibited good correlation and generalization.
The aim of this study is to find the suitable relationship among the flow stress, strain, strain rate and temperature to model high temperature flow stress of 6063 Al alloy. Based on the experimental stress–strain data of isothermal hot compression tests, a constitutive equation including the flow stress, strain rate and temperature considering compensation of strain was developed, and the performance of the developed constitutive equation was also analyzed.
2 Experimental
Commercial 6063 Al alloy was used for the present test using the following chemical composition: 0.7% Mg, 0.423% Si, 0.043% Cu, 0.145% Fe, 0.002% Mn, 0.0127% Ti, 0.046% Cr and balance of Al (mass fraction).
Cylindrical specimens were machined with a diameter of 10 mm and a height of 15 mm. In order to decrease the effect of friction at the specimen-indenter interface during compression deformation, the flat ends of the specimen were recessed to a depth of 0.2 mm to entrap the lubricant of graphite mixed with machine oil. A series of isothermal hot compression tests were conducted on a Gleeble–1500 thermo-simulation machine. The testing temperatures ranged from 573 to 773 K at an interval of 50 K and at constant strain rates of 0.5, 5 and 50 s-1. All specimens were heated up to test temperatures at a rate of 1.7 K/s by thermo-coupled feed-back-controlled AC and hold for 180 s before compression for the purpose of heat balance. The reduction in height is 50% at the end of the compression tests. The load-stroke data obtained in hot compression tests were transformed into true stress–true strain curves.
3 Results and discussion
3.1 True stress–true strain curves
A series of typical true stress–true strain curves obtained during hot compression of 6063 Al alloy at strain rate of 0.5-50 s-1 and deformation temperature of 573-773 K are shown in Fig. 1. It can be found that the flow stress is sensitive to the deformation temperature and strain rate. There is a general trend that the flow stress increased with increasing strain rate at a given temperature, or decreasing the deformation temperature while the strain rate remains unchanged. It can be also seen that the true stress-true strain curves exhibit peak stresses at small strains, and the flow stresses decrease monotonically until high strains. Especially, flow stress softening appears in higher temperature or/and higher strain rate regions, which suggests that dynamic softening dominates over work hardening. These characteristics can be commonly related to the nucleation and growth of dynamically recrystallized grains and dislocation annihilation during hot deformation.
Fig. 1 True stress-true strain curves for 6063 Al alloy at various temperatures with different strain rates
3.2 Constitutive equation for flow stress
In terms of the curvilinear trend of the flow stress, the well-known Arrhenius equation can be used to establish the relationship between the flow stress, strain rate and temperature during hot deformation. Simultaneously, the combined effects of temperature and strain rate on the deformation behaviors can be also represented using Zener–Hollomon parameter, Z, in an exponent-type equation. These equations have been successfully applied to flow stress prediction [9,15]. They are often given by
(1)
(2)
and F(s) can be expressed by the following equations:
(3)
where 
is strain rate; s is the flow stress for a given true stain; Q is the deformation activation energy; R0 is the universal gas constant; T is the temperature; A, a, n and b are the material constants, a=b /n.
3.3 Mathematical analysis for constitutive equation
For the purpose of determining the materials constants of the above constitutive equations, the experimental true stress-true strain data obtained from the compression tests under various deformation conditions were used to analyze the constitutive equation. As an example, the true strain of 0.1 is first taken to present the solution procedures of the material constants.
For low stress levels (as<0.8) and high stress levels (as>1.2), F(s) is substituted into Eq. (2), respectively, Eq. (2) can be expressed as the power law and the exponential law as follows:
(4)
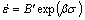(5)
where B and B' are the material constants. By taking logarithms of both sides of Eq. (4) and Eq. (5), the equations can be obtained as follows:
(6)
(7)
By substituting the values of different strain rates and flow stresses at different deformation temperatures into Eq. (6) and Eq. (7), the relationships of 
and 
can be effortless obtained, as shown in Fig. 2. As a result, the mean values of n and b can be determined from the slope of the lines in and plot, respectively, for the range of temperatures studied. Moreover, it can be also observed from Fig. 2 that the lines are almost parallel. The results show that there is a very small variation in the slope of the lines. The slight variation of the slope of the lines which is considered to be due to scattering in the experimental data points should be neglected in this study. Thus, the mean values of n and b are calculated as 9.0439 and 0.1486 MPa-1, respectively. By using the relationship of a=b/n, a was determined as 0.0164 MPa-1.
For all stress levels, Eq. (2) can be also represented as the hyperbolic sine law:
(8)
Fig. 2 Evaluating value of n by fitting 
(a) and b by fitting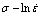 
(b)
For a particular strain rate, differentiating Eq. (8), the deformation activation energy, Q, can be expressed as follows:
(9)
In order to determine the relationship in the plot of ln[sinh(as)] vs T-1, the values of the tested temperature and flow stress for all the strain rates were substituted into Eq. (9) and the slopes of the lines were obtained, as shown in Fig. 3. Thus, the mean value of Q can be obtained under different strain rates. At the true strain of 0.1, the Q-value was found to be 181.8906 kJ/mol.
The logarithm of both sides of Eq. (8) was taken and the value of A was obtained by using the following equation:
(10)
It was clear from Eq. (10) that the values of A for all the tested temperatures can be derived from the intercept of Fig. 3. The mean value of A (at the strain of 0.1) was found to be 1.4506×1014 s-1.
Fig. 3 Evaluating value of Q by plotting ln[sinh(as)] versus T-1
3.4 Material constants as functions of strain
In the above equations, it is apparent that the flow stress is related to both the deformation temperature and strain rate. However, the effect of strain should be also taken into account. It can be evidently found from the true stress–true strain curves of Fig. 2 that the influence of strain on the flow stress is important. Therefore, in the present work, the compensation of strain incorporated into material constants (a, n, Q and A) was adopted to further increase prediction accuracy. The material constants (a, n, Q and A) were assumed to be the polynomial function of strain [16].
In order to know the relationships between material constants and true strain for 6063 Al alloy, the above- mentioned solution procedures were employed to calculate the values of material constants of the constitutive equations under different true strains within the range of 0.05-0.6 and the interval of 0.05. Furthermore, the values of a, n, Q and ln A of 6063 Al alloy can be polynomial fitted by a 4th order as follows:
(11)
where a0–a4, n0–n4, Q0–Q4 and A0–A4 are the coefficients of the polynomial and e is the true strain. The coefficients of the polynomial fitting are listed in Table 1.
Thus, the developed constitutive equation that relates the flow stress to Zener-Holloman parameter can be expressed as
(12)
It is also known from the above analyses that this developed constitutive equation involves material constants (a, n, Q and A) which vary with true strain. Once the polynomial coefficients of all material constants are determined, the flow stress considering the effects of temperature, strain rate and strain can be predicted by the use of Eq. (12).
Table 1 Coefficients of polynomial for a, n, Q and ln A
3.5 Developed constitutive equation performance
The developed constitutive equation (considering the effect of strain) can be used to model the flow stress of 6063 Al alloy during hot deformation. As shown in Fig. 4, the actual prediction values are in good accordance with the experimental data.
It can be also found that different measures of prediction error such as average absolute relative error (AARE) can be used to further evaluate the performance of the developed constitutive equation. The expression of AARE (Er) can be written as follows:
(13)
where k is the total number of data; spre is the value predicted by the constitutive equation; sexp is the value of the experimental data.
In the present study, the value of mean percentage error (AARE) is found to be only 4.65%. As shown in Fig. 5, a good correlation (the correlation coefficient, R=0.97953) between experimental and predicted data is also obtained. From Figs. 4 and 5, it can be concluded that good correlation between experimental and predicted data is obtained other than some deviation due to the scatter in the experimental data. In spite of this divergence, R and Er are found to be 0.97953 and 4.65%, respectively, which reflects the good prediction capabilities of the developed strain compensated constitutive equation. The results indicate that the developed constitutive equation can effectively estimate the high temperature flow stress of 6063 Al alloy and can be used to numerically analyze the hot deformation process of this material.
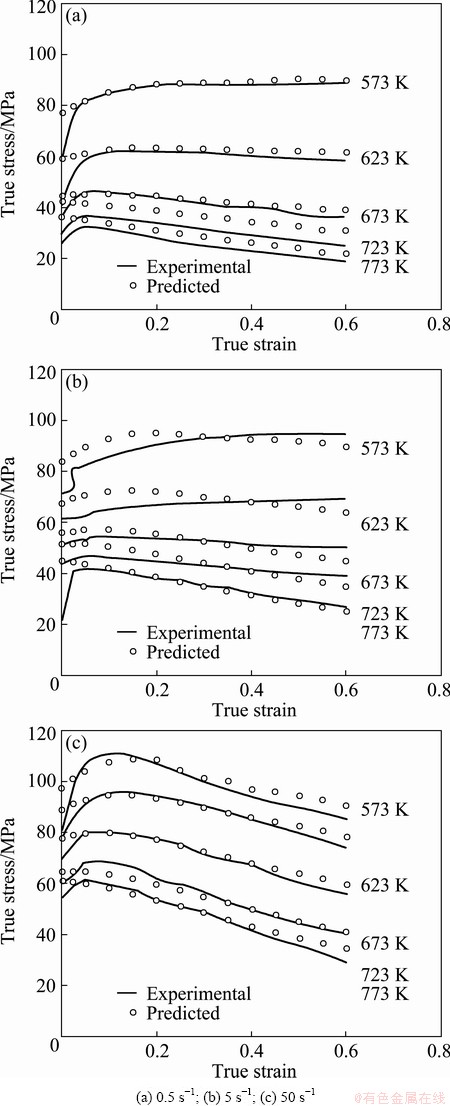
Fig. 4 Comparison between predicted and measured true stress–true strain curves for specimens deformed at different strain rates
Fig. 5 Comparison between experimental and predicted flow stresses of 6063 Al alloy using developed constitutive equation
4 Conclusions
1) Based on the experimental true stress-true strain data, a strain compensated constitutive equation incorporating the effects of temperature and strain rate was proposed to describe high temperature flow stress of 6063 Al alloy.
2) A 4th order polynomial was found to suitably describe the influence of strain on materials constants (a, n, Q and A) in the constitutive equation.
3) A comparison between the experimental and predicted results confirmed that the developed constitutive equation considering the effect of strain had the excellent prediction capabilities. The average absolute relative error (AARE) associated with the prediction over the entire domain was found to be 4.65%.
References
[1] PANIGRAHI S K, JAYAGANTHAN R, PANCHOLI V. Effect of plastic deformation conditions on microstructural characteristics and mechanical properties of Al 6063 alloy [J]. Materials Design, 2009, 6(30): 1894-1901.
[2] PANIGRAHI S K, JAYAGANTHAN R. Effect of rolling temperature on microstructure and mechanical properties of 6063 Al alloy [J]. Materials Science and Engineering A, 2008, 492(1-2): 300-305.
[3] EDGREN F, ASP L E. Approximate analytical constitutive model for non-crimp fabric composites [J]. Composites Part A: Applied Science and Manufacturing, 2005, 36(2): 173-181.
[4] MOMENI A, DEHGHANI K. Characterization of hot deformation behavior of 410 martensitic stainless steel using constitutive equations and processing maps [J]. Materials Science and Engineering A, 2010, 527(21-22): 5467-5473.
[5] SUNG J H, KIM J H, WAGONER R H. A plastic constitutive equation incorporating strain, strain-rate, and temperature [J]. International Journal of Plasticity, 2010, 26(12): 1746-1771.
[6] LIN Y C, CHEN X M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working [J]. Materials Design, 2011, 32(4): 1733-1759.
[7] LIN Y C, LIU G. A new mathematical model for predicting flow stress of typical high-strength alloy steel at elevated high temperature [J]. Computational Materials Science, 2010, 48(1): 54-58.
[8] LI Hui-zhong, WEI Xiao-yan, OUYANG Jie, JIANG Jun, LI Yi. Hot deformation behavior of extruded AZ80 magnesium alloy [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(11): 3180-3185.
[9] SELLARS C M, McTEGART W J. On the mechanism of hot deformation [J]. Acta Metallurgica, 1966, 14(9): 1136-1138.
[10] LIN Y C, CHEN M S, ZHANG J. Modeling of flow stress of 42CrMo steel under hot compression [J]. Materials Science and Engineering A, 2009, 499(1-2): 88-92.
[11] SAMANTARAY D, MANDAL S, BHADURI A K. Constitutive analysis to predict high-temperature flow stress in modified 9Cr-1Mo (P91) steel [J]. Materials Design, 2010, 31(2): 981-984.
[12] HE X M, YU Z Q, LIU G M, WANG W G, LAI X M. Mathematical modeling for high temperature flow behavior of as-cast Ti-45Al-8.5Nb-(W,B,Y) alloy [J]. Materials Design, 2009, 30(1): 166-169.
[13] LI Jian-bo, LIU Yong, WANG Yan, LIU Bin, Bin LU, LIANG Xiao-peng. Constitutive equation and processing map for hot compressed as-cast Ti-43Al-4Nb-1.4W-0.6B alloy [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(11): 3383-3391.
[14] ZHONG J, XIAO Y H, GUO C. Constitutive modelling for high temperature behaviour of 12CrNiMoWV martensitic stainless steel [J]. Materials Science Technology, 2012, 28(6): 719-726.
[15] MCQUEEN H J, RYAN N D. Constitutive analysis in hot working [J]. Materials Science and Engineering A, 2002, 322(1-2): 43-63.
[16] MIRZADEH H, NAJAFIZADEH A. Flow stress prediction at hot working conditions [J]. Materials Science and Engineering A, 2010, 527(4-5): 1160-1164.
考虑应变补缩的6063铝合金高温流变应力本构方程
甘春雷1，郑开宏1，戚文军1，王孟君2
1. 广州有色金属研究院，广州 510650；
2. 中南大学 有色金属材料科学与工程教育部重点实验室，长沙 410083
摘 要：为了建立精确模拟6063铝合金高温流变应力的本构方程，在温度为573~773 K和应变速率为0.5~50 s-1的条件下，采用Gleeble-1500热模拟机进行等温热压缩实验。结果表明：可以采用参数Z描述温度和应变速率对6063铝合金热变形行为的影响，建立的本构方程中的材料常数(a, n, Q和A)可以表示成应变的4次多项式函数。模拟结果表明：所建立的本构方程能精确预测6063铝合金高温流变应力，因此，本构方程适合用于模拟热变形过程，如挤压和锻造，并且可以在工程应用中正确设计变形参数。
关键词：6063铝合金；本构方程；流变应力；应变；热变形
(Edited by Chao WANG)
Foundation item: Project (2012B090600051) supported by Al and Mg Light Alloys Platform on the Unity of Industry, Education and Research Innovation of Guangdong Province, China; Project (2012B001) supported by the PhD Start-up Fund of Guangzhou Research Institute of Non-ferrous Metals, China
Corresponding author: Chun-lei GAN; Tel: +86-20-37238039; E-mail: ganchunlei@163.com
DOI: 10.1016/S1003-6326(14)63492-0
Abstract: In order to develop the appropriate constitutive equation which can precisely model high temperature flow stress of 6063 Al alloy, a series of isothermal hot compression tests were performed at temperatures from 573 to 773 K and strain rates from 0.5 to 50 s-1 on a Gleeble-1500 thermo-simulation machine. Zener–Hollomon parameter in an exponent-type equation was used to describe the combined effects of temperature and strain rate on hot deformation behaviour of 6063 Al alloy, whereas the influence of strain was incorporated in the developed constitutive equation by considering material constants (a, n, Q and A) to be 4th order polynomial functions of strain. The results show that the developed constitutive equation can accurately predict high temperature flow stress of 6063 Al alloy, which demonstrates that it can be suitable for simulating hot deformation processes such as extrusion and forging, and for properly designing the deformation parameters in engineering practice.
